关于平面Ros不等式的几点注记

仇恒方，梅静芳，徐 珂

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

众所周知，几何不等式在研究几何问题时扮演着一个至关重要的角色.一般地，一个几何不等式主要描述几何体的体积、表面积与曲率等几何不变量之间的关系（参见文献［1-3］）.根据几何不变量的性质，几何不等式可分为内在型几何不等式与外在型几何不等式.内在型几何不等式是关于面积、体积、Gauss曲率等内在不变量的不等式，大多数几何不等式属于内在型几何不等式，例如经典的等周不等式、Minkowski不等式等.而外在型几何不等式是关于平均曲率积分等外在不变量的不等式，目前对外在型几何不等式知之甚少.还有一些不等式既不属于内在型几何不等式，也不属于外在型几何不等式，即混合型几何不等式.例如著名的Fenchel不等式与Alexandrov-Fenchel不等式，以及下面的Ros不等式.

引理1［4］（Ros定理）设Σ为嵌入在R3中的紧致闭C2光滑曲面，Σ包含一个体积为V的区域K，如果Σ的平均曲率H恒大于零，则有不等式其中dA为Σ的体积元，等号成立当且仅当Σ为球面.

1990年，Osserman在文献［4］中给出引理1的一个直观的简化证明.2009年，周家足在文献［4］的基础上给出高维Ros定理的一个直观简明的几何化证明.同时，在平面情形下，周家足利用赋范空间中Hölder不等式，证明了二维空间中的Ros定理.

引理2［5］（Zhou）设Γ为欧氏平面R2中的简单光滑闭曲线，Γ所围区域K的面积为A，s为Γ的弧长.如果Γ的曲率κ处处不为零，则

等号成立当且仅当Γ为圆.

称式（1）为关于区域K的Ros等周不等式，并定义整体量为区域K的Ros亏格，记为ΔR(K).

近年来，周家足，马磊等人对平面Ros不等式进行不同程度的加强（参见文献［5-10］）.本文就Γ所围区域是凸域情形下，对Ros不等式进行进一步的加强.

1 预备知识

本节主要介绍积分几何与凸几何分析中的一些相关概念，更多相关知识可参阅任德麟［1］，Schneider［3］等人的著作.

设K是一个平面凸域，其边界曲线为Γ，且假定R2的原点O落在K的内部.令u是一个平面单位向量，l(u)是K关于u的支撑直线，即l(u)与u垂直且与K的边界相接触.从O到直线l(u)的有向距离，记为h(u)，称其为K在方向u上的Minkowski支撑函数.由于u通常可以由x轴到u的有向角θ决定，即u(θ)=(cosθ,sinθ)，所以也可以用h(θ)来代替h(u).容易看到，h(θ)是一个连续的以2π为周期的函数，则Γ可用支撑函数表示如下

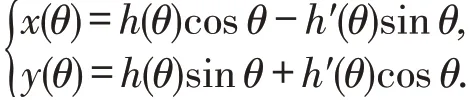
设κ(θ)为光滑严格凸曲线Γ的曲率，ρ(θ)为曲率半径，则因此

其中s为曲线Γ的弧长.

设A为凸域K的面积，则

下面用h(θ)的Fourier级数形式来表示A.因为一个给定的凸域K的支撑函数总是连续有界的，且以2π为周期，所以h(θ)可以展开成如下形式的Fourier级数，即其中关于θ求导可得

利用Parseval恒等式得到

结合式（2）和（3）可得

回顾凸曲线的渐屈曲线（参见文献［11-12］）.曲线Γ的渐屈曲线是它的法线的包络.因此，Γ的渐屈曲线的广义支撑函数为（参见文献［11-12］）.若Ae表示Γ的渐屈曲线所围成的代数面积，则

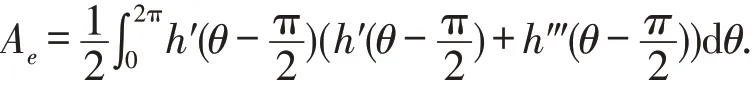
接下来，回顾另外一种曲线，即凸曲线的垂足曲线（参见文献［11-12］）.设Γ~是Γ的垂足曲线，即Γ~在方向u(θ)上的径向距离恰好等于Γ在方向u(θ)上的支撑函数h(θ).因此，得到Γ的垂足曲线在极坐标下的参数方程为r=h(θ).故垂足曲线所围成的面积为再次利用h(θ)的Fourier展开式可以得到

下面考虑一条凸曲线的Wigner焦散线.设Γ是一条凸曲线，p,q是Γ上的两点.若分别过p,q的Γ的支撑线互相平行，则称p,q为Γ的一组平行对.定义其中p,q∈Γ是一组平行对} 为Γ的Wigner焦散线（参见文献［11-12］）.经过简单的计算可知，Γ的Wigner焦散线的支撑函数为若用Aω表示Γ的Wigner焦散线的面积，则

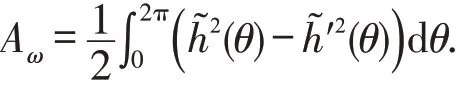
进一步，得到

令

称以s(K)为圆心，以为半径的圆盘为K的Steiner圆盘，记为S(K)，并称s(K)为K的Steiner点（参见文献［3，13-14］）.因此，由h(θ)的Fourier级数知s(K)=(a1,b1).

设K和L是平面上支撑函数分别为h(K,θ)和h(L,θ)的凸域，K和L的Hausdorff度量定义为

文献［3，13-14］还提出其他关于K和L的偏差度量，如L2度量，其定义为

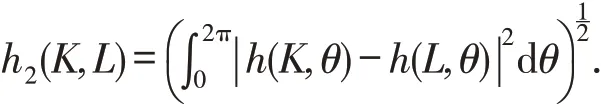
显然，h(K,L)=0（或h2(K,L)=0）当且仅当K=L.

利用Parseval恒等式，K与K的Steiner圆盘S(K)之间的L2度量为

2 主要结果

记ω为从P到∂K的视角，dP为面积测度.当n＞1时，文献［11-12］中有

文献［15］还证明式（10）的另一种等价表示，即

例如，当n=2时，

进一步，有Crofton公式（参见文献［11-12，15］）

定理1设K为平面上C2类的光滑闭凸曲线Γ所围成的凸域，记A为K的面积，ΔR(K)和Aω分别为凸域K的Ros亏格和Γ的Wigner焦散线的面积，则

其中Ae为Γ的渐屈曲线所围成的代数面积，等号成立当且仅当K的支撑函数形式为

证明由式（4）和（5）可得

从而，

进一步，由式（8）（12）和（13）得到

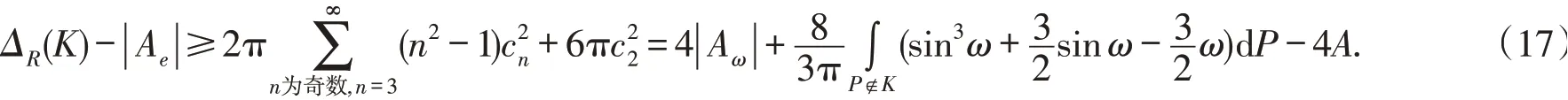
即定理1中不等式（14）成立.

由式（16）和（17）可以看到定理1中等号成立的充要条件为an=bn=0,n≥3.

注1由式（17）易看到定理1中ΔR(K)的下界是非负的.

定理2设K为平面上C2类的光滑闭凸曲线Γ所围成的凸域，记A为K的面积，ΔR(K)和Aω分别为凸域K的Ros亏格和Γ的Wigner焦散线的面积，则

等号成立当且仅当K的支撑函数形式为

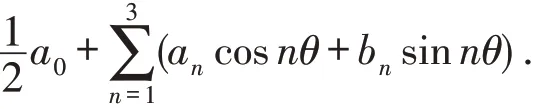
证明由式（8）和（15）可得

从而,

即定理2中不等式（18）成立.

由式（19）可以看到定理4中等号成立的充要条件是：an=bn=0,n≥4.

注2由式（19）易看出定理4中ΔR(K)的下界是非负的.

定理3设K为平面上C2类的光滑闭凸曲线Γ所围成的凸域，记A为K的面积，ΔR(K)和分别为凸域K的Ros亏格和Γ的垂足曲线的面积，则

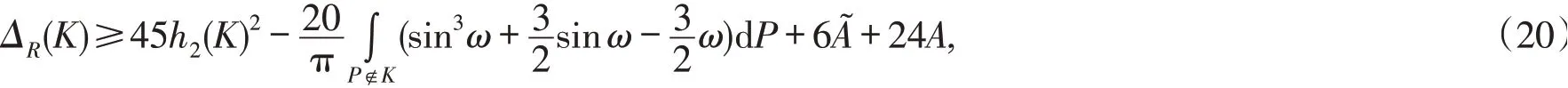
其中h2(K)为K与K的Steiner圆盘S(K)之间的L2度量，等号成立当且仅当K的支撑函数形式为

证明首先，把Steiner点(a1,b1)作为坐标原点，由式（5）（7）和（15）可得

从而，

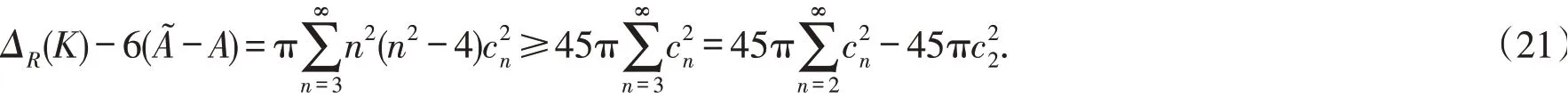
进一步，由式（9）（12）和（13）得到

即定理3中不等式（20）成立.

由式（21）可以看出定理3中等号成立的充要条件为an=bn=0,n≥4.

注3由式（21）易看出定理5中ΔR(K)的下界是非负的.

3 结论

文章在周家足等研究基础上，进一步对平面Ros不等式进行研究.首先用Fourier级数形式来表示Ros亏格，然后经过简单的计算，对Ros亏格的下界进行估计，进而得到它的一些非负下界，最后把这些非负下界分别用垂足曲线的面积、Wigner焦散线的面积及L2度量等表示，并得到相应形式Ros亏格的下界.