抛物线拱面内位移近似解析方法
2021-09-12胡常福刘科李漳
胡常福,刘科,李漳
(华东交通大学 土木建筑学院,江西 南昌330013)
拱结构因其外形美观、承载力及刚度大而在土木工程中广泛使用[1−2]。拱结构的面内线性变形性能,在工程实践中使用最为广泛。圆弧拱的曲率处处相等,易于推演平衡微分方程,针对各种荷载[3−5]、边界条件[6−7]及新材料拱[8−9]的面内非线性变形性能,学者们均开展了较好的研究。由于圆弧拱对应的径向荷载在桥梁工程中应用不多,近年来研究者开始研究直角坐标系下拱结构的变形行为。BRADFORD 等[10]最早提出了抛物线两铰拱面内非线性的解析方法,并进行了试验的验证[11]。蔡建国等[12−13]对抛物线无铰拱的变形行为进行了研究,BRADFORD 等[14]在对抛物线拱面内非线性变形解析的精度检验后发现浅拱假设仅在矢跨比小于1/12.5 才能成立。HU 等[15]提出了一个包含弧长项的应变解决了这个问题,并得到了组合线拱[16]及连拱[17]面内非线性的解析。以上的研究主要集中于拱结构的非线性稳定问题,而桥梁工程中经常使用线性变形的解析,尚未得到有效解决。虽然有限元方法可以较好地计算复杂结构力学的响应,但不易形成符合工程师及规范可接受的实用公式。本文以抛物线拱的面内线性位移为研究对象,提出了一种高精度的近似解析方法,得到了面内竖向位移、水平位移及转角的实用公式,并通过有限元方法验证了实用公式的精确性。
1 抛物线无铰拱面内位移高精度近似解析
1.1 竖向位移高精度近似解析
在如图1所示的笛卡尔直角坐标系下,抛物线拱的线性应变可表示为[15]
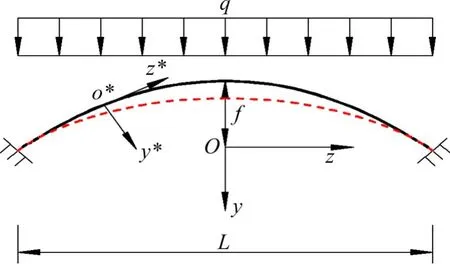
图1 抛物线无铰拱面内变形Fig.1 In-plane deformation of parabolic fixed arch

式中:εm与εb分别为抛物线拱上任一点处的压缩应变和弯曲应变;y*为主拱圈横截面内法线坐标;y为抛物线拱的竖向坐标,y=[z2- (L/2)2]/(2p),z为笛卡尔坐标系的横坐标,p=L2/(8f),L与f分别为抛物线拱的跨度和矢高;w与v分别为抛物线拱变形后的水平位移和竖向位移;(·)′ = d(·)/dz,
处于平衡状态的抛物线拱,若施加一个满足边界条件的虚位移,则外力在位移上所做的虚功与拱结构产生的虚应变能之和为0,即
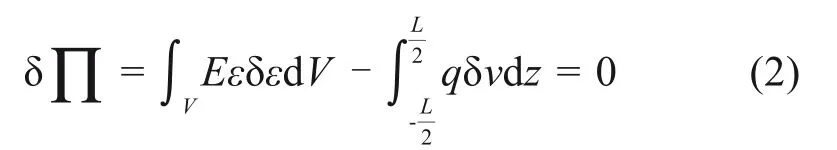
式中:δ(·)为(·)的变分;Π 为拱结构的总虚功;E为拱的弹性模量;ε为抛物线拱的总应变,ε=εm+εb;V为抛物线主拱圈体积,,A为主拱圈截面面积;q为拱圈上的均布荷载。将式(1)代入式(2)并化简,可得
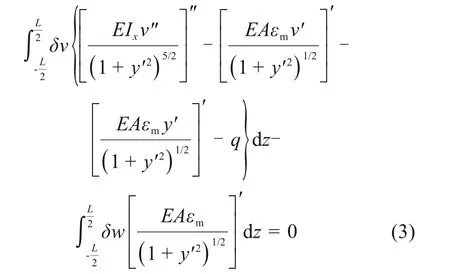
式中:Ix为主拱圈横截面抗弯惯性矩,基于虚位移δw与δv的任意性,由式(3)可推演出
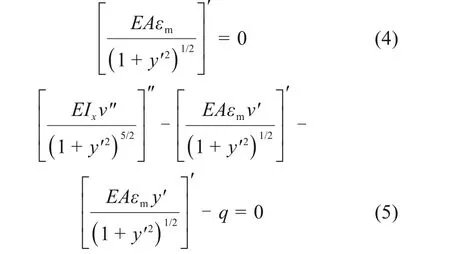
根据欧拉伯努利梁与抛物线拱理论[18]可知,-EAεm为主拱圈的轴力N,N(1+y′2)-1/2为拱脚水平推力H。因此,式(4)可以推演得到

将式(6)代入式(5),可得
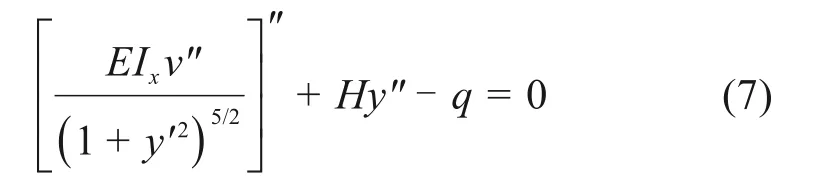
将拱轴线方程代入式(7),可得
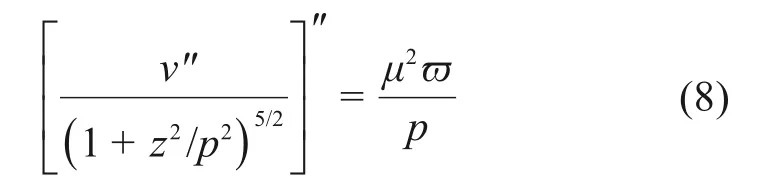
式中:ϖ与μ为无量纲荷载与轴力参数,其定义为

如式(8)所示的平衡微分方程,虽然形式简洁但不能求得显示解析。为此,将方程左边分母中的弧长微分项(1+z2/p2)5/2进行泰勒展开,得到如式(10)所示的近似平衡微分方程
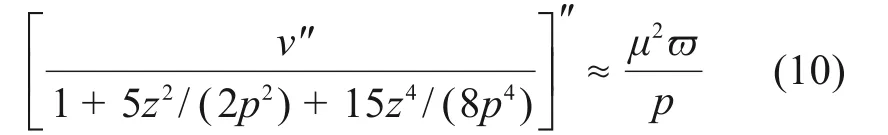
抛物线无铰拱的边界可表示为
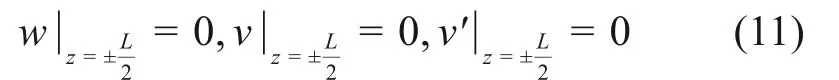
式(10)在满足如式(11)所示的边界下的解为
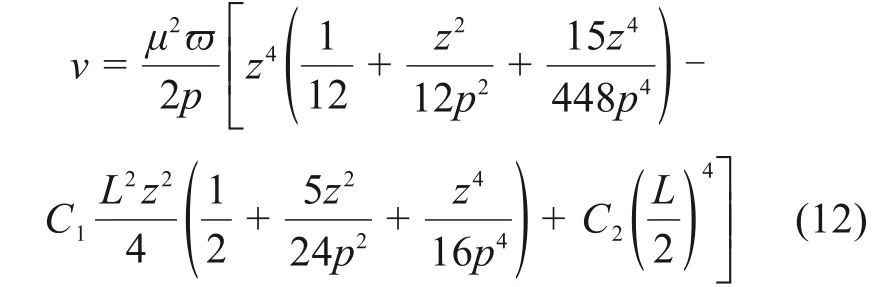
式中:C1与C2为竖向位移系数,表示为
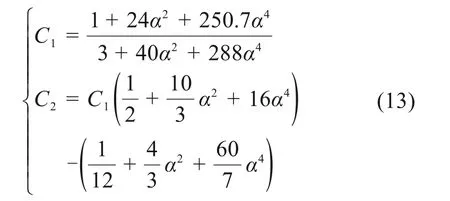
式中:α为抛物线拱的矢跨比。
在如式(10)所示的平衡微分方程中,有2 个未知的参数μ和ϖ。因此,需要增加一个方程来联立求解这两个参数。由式(12)计算的竖向位移,尚需满足另一个基本条件:基于式(1)计算的抛物线无铰拱压缩变形,应与根据式(6)计算得到的压缩量相等。该条件可表示为
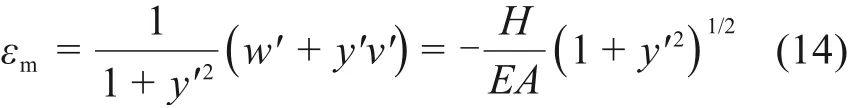
将拱轴线方程代入式(14),对等式两边同乘1+y′2化简后并积分,可得

对于抛物线无铰拱,式(15)的右边积分难以得到显示表达式。近似积分方法[18−19]将弧长微分项近似为双曲余弦函数,可以得到该类问题的实用解析表达

式中:a为悬索线拱形系数;ch(·)为双曲余弦函数。将式(9),(11),(12)及(16)代入式(15),可得
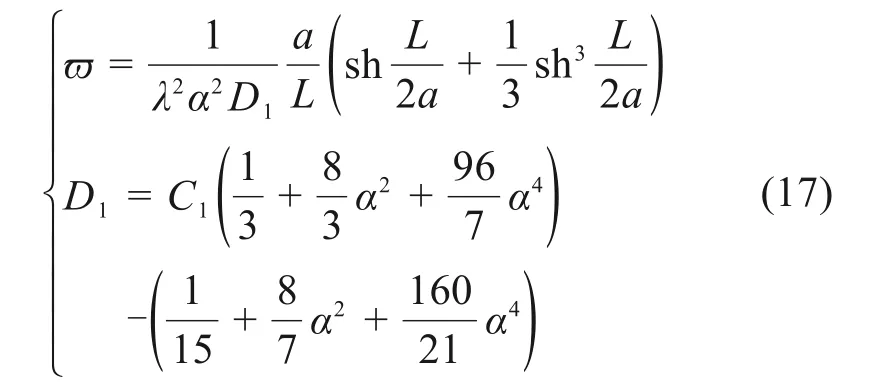
式中:sh(·)为双曲正弦函数;λ=L/ix,为抛物线拱的长细比;为主拱圈截面的回转半径。ϖ系数的具体数值,如表1 所示。为推导拱脚处水平反力的表达式,式(9)可以重写为

表1 抛物线无铰拱ϖ系数Table 1 Parameter ϖ of fixed parabolic arches
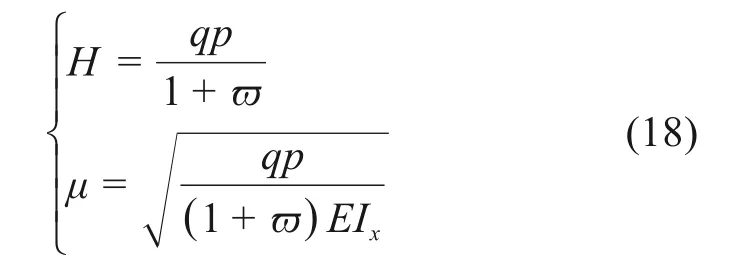
将式(17)及(18)代入式(12),可得抛物线无铰拱竖向位移的表达式为

从而,拱顶竖向位移vc可表示为
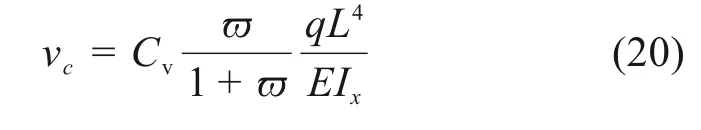
式中:Cv为抛物线无铰拱拱顶竖向位移系数,其表达式如式(21)所示,具体数值如表2所示。


表2 抛物线无铰拱位移系数Table 2 Deformation coefficients of fixed parabolic arches
1.2 水平位移高精度近似解析
对式(1)中压缩应变εm的等式两边同乘1+y′2,再对两边进行积分,可得抛物线拱水平位移为
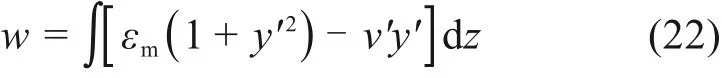
将式(9)及(6)代入式(22),可得

将式(11)、(18)及(19)代入式(23),可得
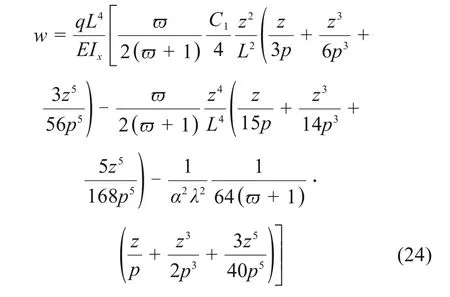
抛物线无铰拱的水平位移一般在跨径四分点附近达到最大,因此四分点处的水平位移有较大的工程参考价值。由式(24)可得

式中:Cwa和Cwb为抛物线无铰拱四分点水平位移系数,其表达如式(26)所示,具体数值如表2所示。
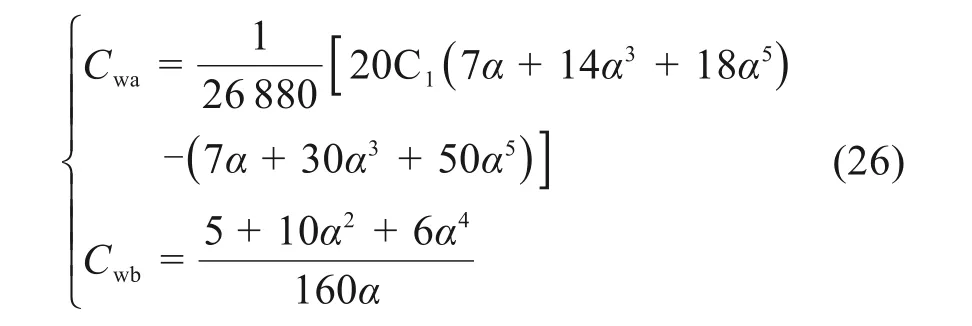
1.3 转角变形高精度近似解析
如图2 所示,抛物线拱上任意点A的切线与水平方向的夹角为φ,在外荷载作用下点A发生了转角θ。因此,变形后A′点的夹角变为φ+θ。由变形前后的几何关系,可得
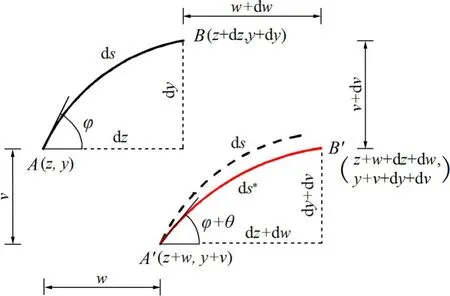
图2 弧微元变形示意图Fig.2 Deformation of infinitesimal curve arc differential element

根据三角函数和差公式,转角的正切值可表示为
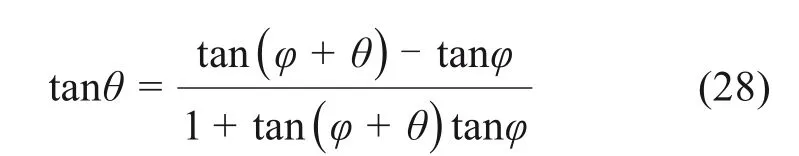
将式(27)代入式(28),可得
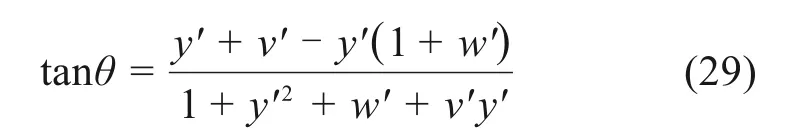
在线性小变形条件下,拱结构转角θ是一个无穷小量,θ≈tanθ成立;水平位移远小于微元水平方向长度,w′<< 1 成立;竖向位移远远小于拱轴坐标,y′v′<< 1+y′2成立。基于以上假定,式(29)可简化为

将式(19)代入式(30),可得到抛物线无铰拱转角变形的解析表达式为
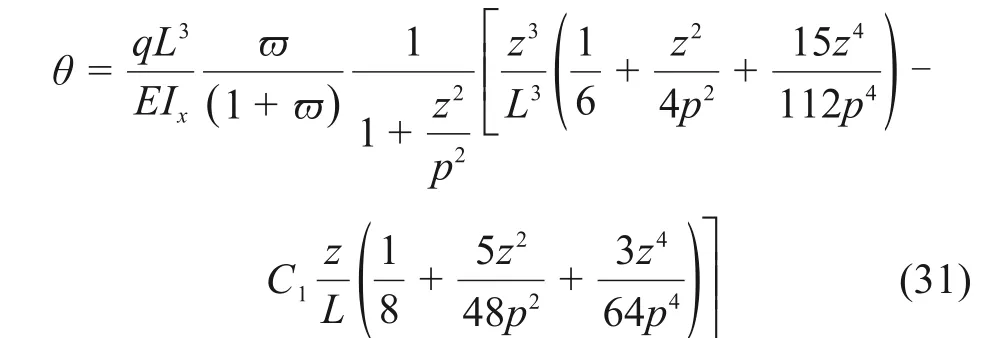
抛物线无铰拱转角变形的最大值一般在跨径四分点处附近。因而,四分点处转角有较大的工程参考价值。由式(31)可得

式中:Cθ为抛物线无铰拱四分点转角位移系数,其表达如式(33)所示,具体数值如表2所示。

2 算例验证
以一跨径为150 m 的抛物线无铰拱为算例,来验证本文提出的面内位移高精度近似解析。该无铰拱矢跨比f/L= 1/5,长细比λ= 120;主拱面积A= 0.866 m2,截面惯性矩Ix= 1.3532 m4;主拱圈材料的弹性模量E= 210 GPa,泊松比υ= 0.2。
拱上所受均布荷载q=200 kN/m,根据文献[15]的研究成果,在该荷载作用下抛物线无铰拱仍处于弹性阶段,不会出现面内非线性现象及屈曲问题。
采用有限元软件ANSYS 建立如图3 所示的有限元模型。该模型含有500 个BEAM4 梁单元,节点沿水平坐标均匀分布,在节点上施加相同的节点力用以模拟均布荷载;为防止拱发生面外变形,约束了所有节点的面外自由度;并在拱脚处约束所有自由度以模拟固结。分别提取有限元数值结果中的各节点面内竖向位移、水平位移及转角变形,并与本文解析结果进行对比,两者对比结果如图4及表3所示。
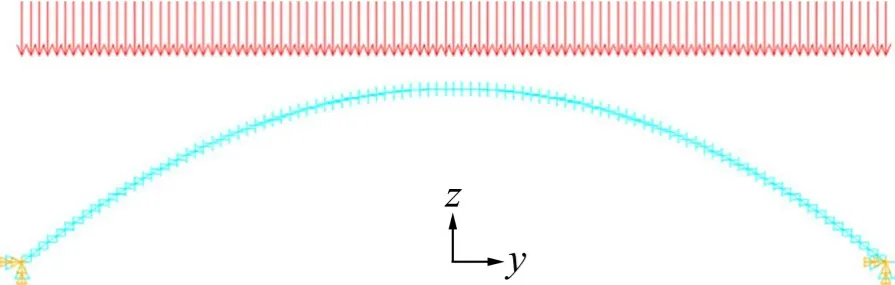
图3 有限元模型Fig.3 Details of finite element formulation
由图4 及表3 可以看出,本文提出的近似解析解均与有限元结果吻合较好。其中,竖向位移误差最小,拱顶处竖向位移相对误差为0.54%,具有较高的精度;转角变形次之,四分点处转角变形相对误差为4.70%,满足实际工程使用的要求;水平位移总体吻合较好,在极值处有一定的误差,四分点处水平位移相对误差为8.73%,考虑到水平位移的量级约为跨径的1/10 000,该近似解析已满足工程实际使用的精度要求。造成水平位移与转角变形产生误差的根本原因是,为得到具有解析表达的面内位移结果,采用了如式(1)所示的简化弯曲变形表达式,忽略了其中的水平位移项,进而造成了水平位移及转角变形的误差。
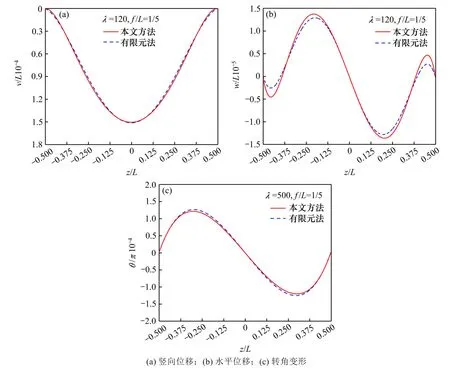
图4 近似解析精度验证Fig.4 Verification of proposed analytical solutions

表3 面内位移极值比较Table 3 Comparisons of maximum magnitudes of in-plane deformation
由面内位移的解析表达式可以看出,矢跨比与长细比是抛物线无铰拱面内位移的2个重要影响参数。为此,以上述算例为基础,调整其中的矢跨比与长细比(如表4 所示),用以在更大范围内校验本文近似解析的精度。基于这些参数,分别使用本文近似解析与有限元方法计算抛物线无铰拱的面内位移。2 种方法计算的拱顶竖向位移、四分点水平位移与转角变形结果对比,如图5 与图6所示。

表4 比选参数范围Table 4 Parameter ranges of verification
由图5与图6可以看出,在矢跨比1/3~1/10及长细比40~200的大范围内,本文近似解析得到的抛物线无铰拱面内位移均与有限元结果吻合较好,表明本文方法具有较好的精度。
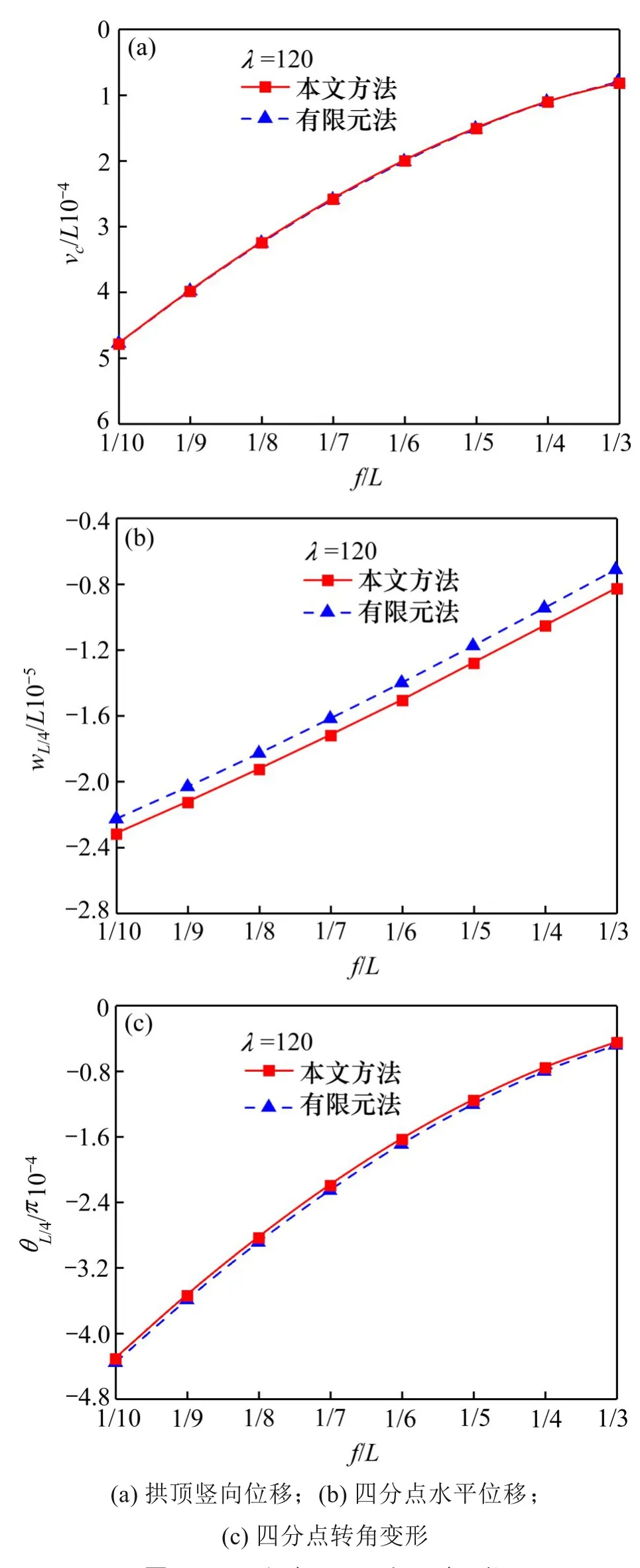
图5 不同矢跨比下面内位移比较Fig.5 Comparisons of different rise-to-span ratios

图6 不同长细比下面内位移比较Fig.6 Comparisons of different slenderness
3 结论
1) 本文提出的近似解析方法,可得到抛物线无铰拱面内位移的高精度近似解析。
2) 矢跨比与长细比,是抛物线无铰拱面内位移的重要影响参数。
3) 提出的抛物线无铰拱拱顶竖向位移、四分点水平位移及转角变形解析表达式,满足桥梁工程实际使用的精度要求。
