基于离散元法的列车运行速度对有砟道床工作性能影响的研究

2021-09-12陈宪麦陈楠王日吉张向民王卫东

铁道科学与工程学报 2021年8期

陈宪麦，陈楠，王日吉，张向民，王卫东

(1. 中南大学土木工程学院，湖南长沙410075；2. 重载铁路工程结构教育部重点实验室，湖南长沙410075)

有砟轨道作为轨道结构的一种常用类型[1]，为了保证列车在运行过程中的安全性与可靠性，近年来有许多学者在离散元的基础上对有砟结构进行模拟和分析。张徐等[2]将轨枕用长方体刚性颗粒簇进行模拟，对道床的动态行为进行了分析研究；曾志平等[3−4]将轨枕简化为长方体，并用墙体模拟轨枕，对有砟道床的阻力特性、振动荷载作用下道床的力学性能进行研究；王桐等[5−6]用离散元方法对有砟道床的动态行为及其沉降进行研究；崔旭浩等[7]用clump 单元模拟道砟颗粒和轨枕，用ball单元模拟钢轨和扣件，对轨道结构道床板结的动力性能进行二维模拟研究；SHI等[8]采用离散元-有限元相结合的方法，模拟和研究有砟轨道的刚度和力学行为；井国庆等[9]采用离散元法模拟高速铁路有砟道床，分析不同列车运行速度下道床横向阻力的变化情况；KHATIBI 等[10]用离散元法分析道床深度、砟肩宽度和高度、道砟材料内颗粒间摩擦力，以及道床孔隙率对道床横向阻力的影响。现有的轨道结构离散元模拟方法中，比较精确的是用激光扫描道砟颗粒形成三维网格，将其导入到PFC软件中并用软件自带的bubblepack算法形成clump道砟颗粒，轨枕的模拟大多采用形状较为规则的长方体或楔形体。本文在既有研究方法的基础上，考虑了轨枕的真实几何形状，用clump单元模拟轨枕的不规则形状；对道床进行了横向阻力与纵向阻力的试验，并用离散元法进行模拟，以验证模型的可靠性，在此基础上对轨道结构模型进行动力研究和分析，通过在承轨台处施加正弦荷载，模拟和分析道砟颗粒在不同列车速度下的位移、加速度随道床深度和横向不同位置的变化情况。

1 有砟道床的离散元模型

1.1 道砟颗粒

道砟颗粒的真实形状极不规则，很难用数学公式对其进行表达。为了能够相对精确地模拟颗粒形状，对道砟颗粒进行三维激光扫描，形成三角形网格，并将该网格导入到PFC 中形成道砟颗粒模板(见图1)，以此模板进行道砟颗粒模拟。所选取的4 个颗粒模板中，除了第2 个模板较为扁平接近针片状外，其余3个模板基本上都比较圆润或接近方形，均较具有代表性。

图1 道砟颗粒模板Fig.1 Ballast particle template

1.2 轨枕模型

目前大多数文献对轨枕模型采用的模拟方法大致分为2 类，一类是将轨枕近似为长方体[11−14]，并用wall 或clump 进行模拟；另一种是直接用wall单元模拟轨枕的实际外形[15]。而本文将上述2 种方法相结合，不仅用clump模拟轨枕，又考虑了其实际外形尺寸，使仿真模型与实际情况更加接近。

本文采用混凝土Ⅲ型轨枕(长2.6 m)[16]，将代表轨枕几何形态的STL 文件导入到PFC 中，并用clump刚体单元模拟轨枕，模拟结果如图2所示。

图2 轨枕的离散元模型Fig.2 Discrete element model of sleeper

1.3 道床模型

本文根据现行的规范[17]进行轨距和道床尺寸的选取。道床顶宽3 500 mm，道床厚度350 mm，砟肩坡度为1:1.75，砟肩堆高150 mm，轨枕中心顶面与道床顶面齐平，并选取一个轨距的纵向长度(600 mm)作为研究对象。最终的道床离散元模型如图3所示。

图3 有砟道床的离散元模型Fig.3 Discrete element model of ballast bed

1.4 模型参数选定

为使道床离散元模型与实际工况下的工作性能接近，参考既有的研究成果[2−3,7]，并结合试验数据进行验证，最终选定道床模型参数(见表1)，其中，约束墙体代表相邻道砟对研究区域的作用。

表1 离散元模型的细观力学参数Table 1 Micromechanical parameters of the discrete element model

模型中考虑到轨枕与道砟颗粒的材料及其属性，设置轨枕的刚度值比道砟的偏大；同时，为了避免在程序运行过程中道砟颗粒穿过约束墙体，使颗粒与墙体间的接触刚度略大于道砟颗粒本身的接触刚度。

2 模型验证

对有砟道床进行横纵向阻力现场测试试验，将试验数据与离散元仿真模拟结果进行对比，如图4所示。在正常轨道条件下，混凝土轨枕位移小于2 mm 时，道床横纵向阻力成近线性增长[18]，所以本文取轨枕位移为2 mm 时的阻力为道床的横纵向阻力。

从图4 可得，有砟道床横向阻力−位移图的试验拟合曲线与离散元模拟的拟合曲线吻合较好，尤其在2 mm 时几乎接近；而纵向阻力−位移图的试验和模拟拟合曲线几乎重合，所以可初步认为模型与实际相吻合。

为进一步验证模型的可靠性，本文通过最小二乘法对试验和模型数据进行拟合，拟合曲线见式(1)～(4)。

式中：x代表道床轨枕的横纵向位移；y代表与之对应的阻力。

式(1)和式(2)分别是横向阻力−位移图(图4(a))中的试验拟合曲线公式和模拟拟合曲线公式；式(3)和式(4)分别是纵向的试验与仿真拟合曲线公式。

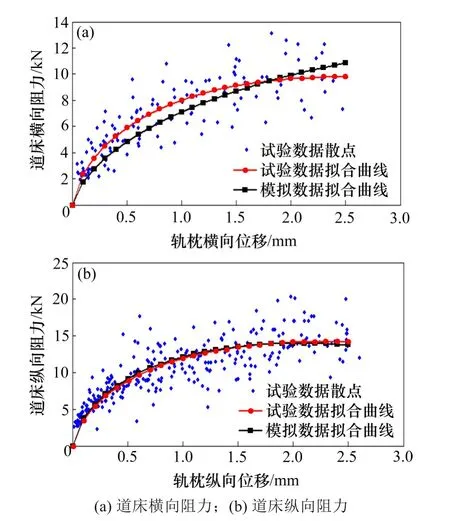
图4 有砟道床的纵横向阻力Fig.4 Discrete element model of ballast bed

根据上述表达式，在横向位移为2 mm 时，道床横向阻力的实测值与模拟值分别为9.633 kN 和9.918 kN，模拟与试验结果的误差为2.95%；纵向阻力的实测值与模拟值分别是14.114 kN 和13.984kN，结果误差为0.92%。模拟值与实测值的差值在误差允许范围内，所以认为该离散元模型是可靠的，可以在此模型的基础上进行后续研究。

3 行车速度对道床性能影响分析

3.1 选定枕上荷载

有砟道床在列车作用下会产生振动、道砟飞溅、道床沉降，导致其几何形态发生变化，甚至使道砟粉化，严重影响道床的使用性能。而道床在不同的列车速度下的响应是不同的，因此，研究列车运行速度对有砟道床的影响是有重要意义的。

本文分别考虑列车速度为60，80，100，120，160和200 km/h时的道床响应。

设计规范[19]规定，重载铁路的列车运行速度不超过100 km/h，因此，60，80 和100 km/h 的列车速度采用重载列车的轴重(27 t)进行加载；120，160 和200 km/h 的列车速度采用17 t 轴重加载，重力加速度g取9.81 m/s2。

参考强度检算相关规范[20]，在列车运行情况下，轨枕动压力Rd的计算公式如下：

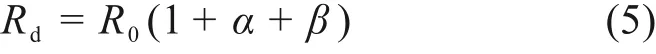
式中：R0为静态枕上压力；β为偏载系数，本文研究对象是直线区段单元，β取值为0.0；α代表速度系数，列车运行速度V≤160 km/h 时α= 0.6V/100，V> 160 km/h时α= 1.0。

对离散元模型进行动力仿真时，在轨枕承轨位置施加正弦荷载Ft，计算公式[21]如下：

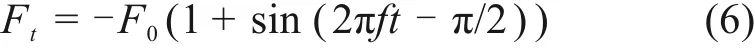
式中，F0为枕上压力半峰值；f为加载频率，为了减少计算机运行时间，此处取100 Hz；t为加载时间，在整个加载过程中，正弦荷载的方向始终竖直向下；不同列车运行速度工况下施加的正线荷载如图5所示。

图5 施加的正弦荷载Fig.5 Diagram of the sinusoidal load applied

通过在轨枕上施加正弦荷载，分析道床在不同车速下的动力响应，动荷载峰值根据规范计算得出；低车速下(60，80 和100 km/h)选择列车轴重为27 t，施加的正弦荷载半峰值分别为90，98 和105 kN；高速下(120，160 和200 km/h)选择轴重为17 t，荷载半峰值分别为72，82 和83 kN，整个加载周期内，正弦荷载均竖直向下。

为了保证列车运行的安全性和可靠性，列车运行速度越快，要求其车体轴重越小。120，160和200 km/h 的车速采用的轴重为17 t，导致列车运行所产生的枕上压力比27 t轴重产生的压力小；但是，在相同轴重下，列车运行速度越大，轨枕承轨位置所施加的正弦荷载峰值越大。

3.2 行车速度对道砟加速度的影响

本文采用离散元模拟方法，通过在轨枕上承轨位置施加正弦荷载，模拟和分析道床在不同列车速度下的动力性能响应。利用离散元软件中自带的history 功能，分别对有砟道床不同深度的道砟进行监测，并记录其在不同车速下的加速度。为使结果更精确，每层道床深度均取3个道砟颗粒进行记录，最终取三者监测的平均值作为本层道床深度的加速度。

列车速度为80 km/h 时，不同深度的道砟颗粒加速度随加载时间的变化趋势见图6。

图6 不同深度的道砟加速度随时间变化Fig.6 Diagrams of the acceleration of ballasts at different depths over time

图6 显示了道床深度为0.1，0.2 和0.3 m 时对应的道砟加速度，由图6可知：在车速相同的情况下，道床加速度随着深度的增加而减小，即由动荷载所产生的加速度在有砟道床中随道床深度逐渐衰减。

图6展示了道床竖向的道砟加速度随时间的变化，而图7则给出不同横向位置的道砟加速度变化情况。图7 是列车速度为80 km/h；道床深度为0.1 m的工况下，不同横向位置处道床的加速度。

由图7 可知，轨下位置处的道砟加速度最大，约为11g(g为重力加速度，取值9.81 m/s2)；道床中心和砟肩处的加速度相对较小。列车80 km/h 对应的加速度约为1g[2]，100 Hz 时的道砟加速度约为10 Hz时道砟加速度的10倍，可以看出，本文所建模型的模拟结果是可靠的。

图7 不同横向位置的道砟加速度变化Fig.7 Ballast acceleration change diagram at different lateral positions

图8 给出了不同车速下，0.1 m 道床深度处的道砟加速度随道床横向位置的变化情况。其中，道床横向位置3，4 和5 分别代表道床中心、右轨轨下位置、右道床砟肩。

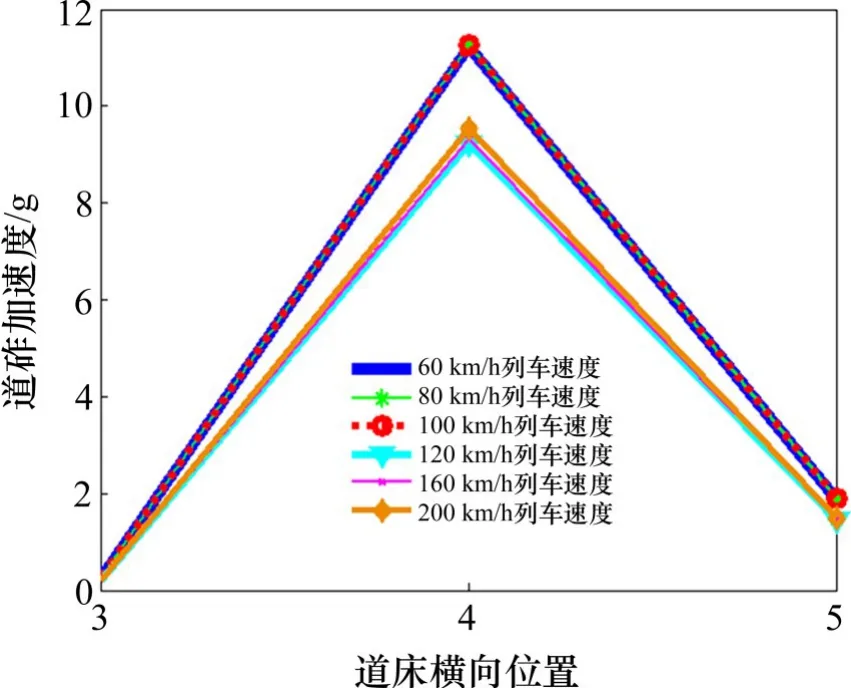
图8 不同车速下道砟加速度随道床横向位置变化Fig.8 Change of ballast acceleration with the lateral position of the ballast bed at different speeds

由图8可知：不同车速下，道砟加速度在道床横向位置的变化趋势相同，均是在轨下位置的道砟加速度最大，在道床砟肩处的道砟加速度次之，道床中心处的加速度最小。在车速相对较高的3种工况下(120，160 和200 km/h)，由于其轴重小，所施加的荷载小，所以在这3种工况下的道砟加速度均小于车速较低的3 种工况(60，80 和100 km/h)。对相同轴重而言，不同车速的道砟加速度响应不同，加速度随车速的增大而增大，但相差很小。

3.3 行车速度对道砟位移的影响

本文对轨枕施加竖向正弦荷载，并对不同工况下平衡状态的道砟位移进行记录。

图9展示了道床横纵截面的位移矢量图。由图可知：道床表面的道砟位移大于内部道砟的位移值；尤其是道床砟肩颗粒的位移，由于在该处道砟不受约束位移量较大，甚至出现了少量的飞砟现象。从道床纵截面位移图可知：在动荷载作用下，道砟颗粒均有向外的运动趋势；轨枕周围的道砟颗粒由于受到荷载的扰动而出现较大的位移量，而外层的道砟颗粒由于受到墙体的约束作用位移相对较小。

图9 有砟道床的位移矢量图Fig.9 Displacement vector diagram of ballast bed

60 km/h 列车速度下，道砟位移量随道床深度的变化趋势如图10 所示。图中道砟位移负值代表道砟颗粒向下运动，正值代表道砟颗粒向上运动。

图10 道砟位移随道床深度的变化Fig.10 Change of ballast displacement with the depth of the ballast bed

根据上述分析结论，由于道床中心和砟肩位置的道砟加速度相对较小，导致道床中心和砟肩处的道砟颗粒随道床深度的变化趋势较为稳定；而轨下位置的道砟加速度较大，使得该处的道砟颗粒位移随深度的变化趋势不明显，但位移扰动不大，相邻测量深度之间的最大位移差为3 mm。在轨枕周围的道砟扰动较大(由图9 可知)，导致右轨下道床深度为0.05 m 和0.1 m 时的道砟位移值较大；0.1～0.3 m 道床深度之间，钢轨处的外荷载随道床深度逐渐衰减，导致轨下道砟位移也随深度递减；轨下0.35 m 深度的道砟受到底部边界约束、周围颗粒、动荷载等多种作用，导致其扰动较大，位移也增大。

由图10 可知：在外荷载作用下，道床中心表面的道砟颗粒出现少量的臌胀现象(道砟位移矢量为正值)；随道床深度的增加，颗粒在动荷载和上部道砟作用下逐渐向下运动，但由于外荷载和颗粒加速度随着道床深度逐渐衰减，导致道砟的位移量也随着道床深度的增加而减小。

不同轴重下，0.2 m 道床深度处的道砟位移值随车速的变化趋势如图11所示。

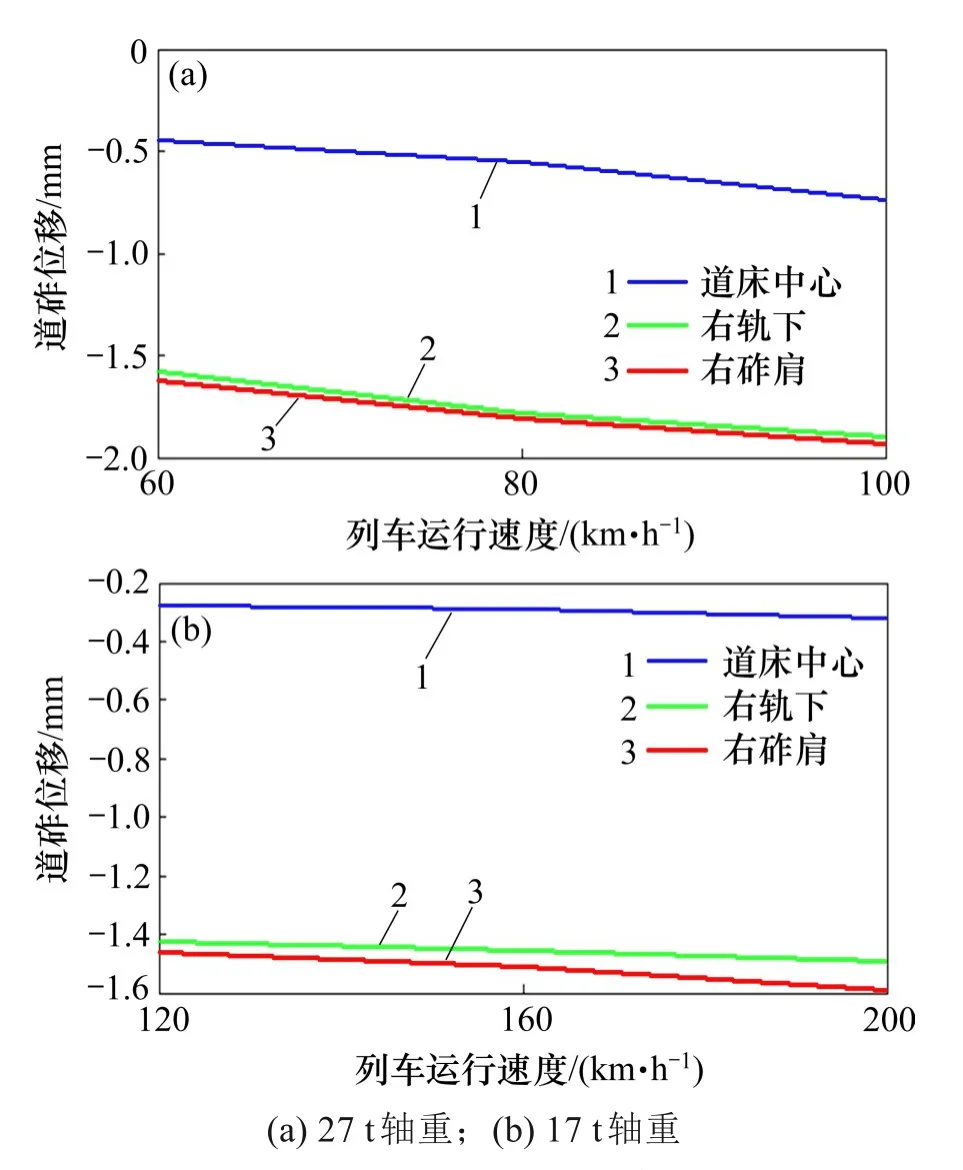
图11 不同轴重下道砟位移随列车速度的变化Fig.11 Variation diagram of ballast displacement with train speed under different axle loads

由图11 可知：列车轴重相同时，道床不同横向位置的道砟颗粒位移均随着车速的增加而增大，且变化趋势相同；在2种不同轴重工况下，由于道床砟肩的道砟颗粒所受的约束小，所以砟肩位置的道砟位移值大于道床中心和轨下位置的道砟位移值；道砟颗粒位移27 t轴重工况下，颗粒的最大位移约为2 mm，17 t 轴重工况下的颗粒最大位移值为1.6 mm。不同工况下的道砟颗粒位移均在允许范围之内。