基于多灰色模型对比的累计前景理论的铁路路线方案优选

刘舒逸，方玺

(武汉理工大学 理学院，湖北 武汉430070)

铁路路线方案的优选为典型的多目标决策问题[1−2]。以往为避免主观因素的影响，多采用确定型客观分析方法对铁路路线进行方案优选[3−4]。但实际上，决策者的非理性主观因素往往会对方案优选决策有很大影响。由于决策时间的变化，不同时间点下某些指标因素是动态变化的，因此以动态的思维分析指标因素的影响，将更加符合实际。多灰色模型对比的累计前景理论，对于局势随时间变化的多目标优选决策问题，有较高的建模及处理能力。将局势决策中的时变指标变为灰数，利用多种灰色预测模型进行精度对比优选以对灰色指标进行准确预测[5−6]，充分考虑了时间变化对方案优选决策的影响[7]。通过分析决策者无意识的决策行为，将概率转化为优选决策时的动态化的指标权重函数，从而获得决策的优势信息[8−10]。该方法通过考虑客观存在的人为非理性主观因素，以体现客观现实的实际情况，因而得到的方案优选结果也更加贴近客观实际[11−13]。多灰色模型对比的累计前景理论首创性的考虑了时间变化对决策局势的动态影响。方法创新性强，考虑更为全面，分析过程贴近实际，分析结果也更加科学可靠。

1 系统建模

1.1 指标系统构建

根据相关文献研究成果[14]，铁路路线优选决策为2 级指标层次结构，1 级指标包括经济、技术、环境及社会等方面的指标。每个1级指标又可以分为若干2 级指标。其一般性指标层次结构见图1[15]。

图1 指标层次结构Fig.1 Indicator hierarchy diagram

以上指标可在铁路方案优选决策时，根据具体情况进行增删补减灵活调整。决策分析时尽量采取量化指标。当部分指标难以直接采用数值进行度量时，可采用德尔菲评分法。

1.2 多灰色模型对比的累计前景理论多目标决策

1.2.1 灰色预测型决策矩阵构建

铁路路线方案优选决策问题一般由n个备选方案构成决策方案集S={S1，S2，…，Sn}，由m个影响指标构成指标集C={c1，c2，…，cm}，则方案Si的指标cj的指标值为xij，得到铁路路线方案优选的决策矩阵X如下：

决策矩阵中的部分指标数值随时间而变动，即为灰色指标，灰色决策矩阵X(⊗)如下：

式(2)中，⊗代表矩阵、数值为随时间而动态变化的数，即灰数。

1.2.2 灰色指标白化处理

灰色指标可采用GM(1,1)模型、微分verhulst模型及差分verhulst 模型进行预测。GM(1,1)模型如下：

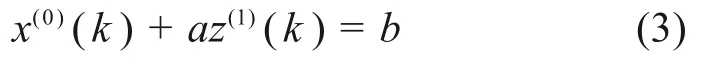
微分verhulst模型如下：

差分verhulst模型如下：

为了提高精度，本文选择GM(1,1)模型、微分verhulst 模型及差分verhulst 模型等3 种模型中的残差平方和最小的模型进行预测白化。

1.2.3 指标规范化处理

决策矩阵X中的指标值有3 种类型：效益型指标、成本型指标及区间型指标。效益型指标值越大，方案越优；成本型指标值越大，方案越劣；区间型指标为值落在某一区间，方案较优。采用[−1,1]的线性变换算子进行规范化处理。

首先，进行j指标均值算子rj计算：

对于效益型指标的规范化处理：

对于成本型指标的规范化处理：

对于区间为(xⅠ,xⅡ)的区间型指标(指标值落在特定区间为好的指标)的规范化处理：

得到规范化处理后决策属性矩阵U：

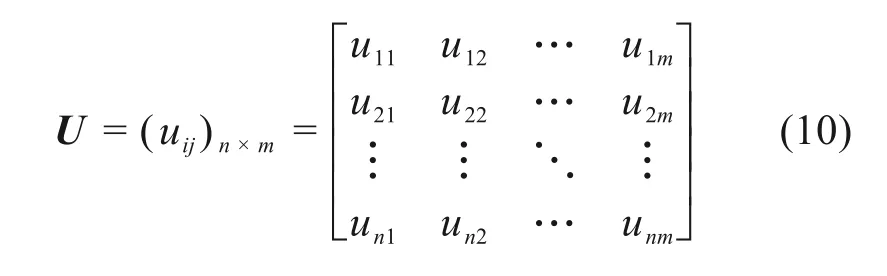
1.2.4 综合前景值计算

根据矩阵U，得到铁路路线方案优选决策局势的正理想方案向量负理想 方 案向 量其 中

计算方案Si的指标cj与正理想方案的关联度：

计算方案Si的指标cj与负理想方案的关联度：

方案Si的指标cj的正前景效用价值函数为：

负前景效用价值函数为：

则方案Si的综合前景值为正、负前景值之和Qi，即：

在式(15) 中， 指标权重向量为W=(w1,w2,…,wj…,wm)。

式(11)～(17)中，ε 取值范围0～1，α取值为0.88；β取值为0.88；θ取值为2.25，γ+取值为0.61，γ−取值为0.69。

1.2.5 最优方案解析优选分析

若权重向量W=(w1,w2,…,wj,…,wm)中各指标权重值为动态未知量。则可得到所有备选方案累加综合前景值Qt的最大化模型：

此模型为非线性规划模型，其约束条件为：

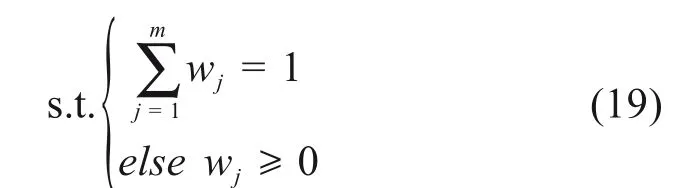
通过解算最大化模型，得到Qt最大化下的最优权重向量

将最优权重向量代入式(15)，得到各方案综合前景值。最优方案S*的综合前景值为Q*：

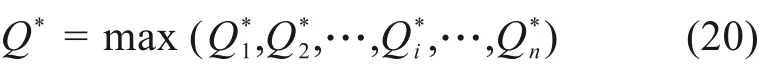
2 例证分析

2.1 项目背景

某拟建城际铁路穿越城市、郊区、乡村等多种类型地域，部分路段离生态敏感区较近。经过前期方案对比初选，初步拟定了1 号，2 号，3 号及4 号4 条铁路路线方案。由于地方政府财政资金压力，导致该项目上马时间不定。目前，认为该项目可能开建的时间为2023 年，2025 年和2030年。

本次铁路路线方案优选决策选取了经济、技术及环境3 个1 级指标，经济可行性选取了建设项目投资C1，经济效益C2；技术可行性选取了土石方工程量C3，桥梁及隧道长度C4，工程地质情况C5；环境可行性选取了生态环境破坏影响C6，拆迁征地面积C7，文物古迹影响C8等2 级指标。其中，C1，C2，C3，C4和C7为定量指标；C5，C6和C8为定性指标，采用专家评分进行间接量化表征(100分制，评分越高，方案越优)。又有C1，C2和C6为灰色指标，其余指标为确定型指标。统计得到各铁路路线方案指标数据，见表1。

从4 个方案指标值看，虽然方案1 和方案3 相对来说有明显不足，但是方案1 和方案3 的某些指标向好的发展趋势明显强于方案2 和方案4，从趋势上存在有逆转或逆袭的可能性，从未来与发展的眼光考虑，仍然将方案1 和方案3 作为备选方案。

2.2 决策矩阵白化及规范化

对灰色指标采用GM(1,1)、微分verhulst 及差分verhulst 模型进行精度对比。1 号方案的建设项目投资C1指标说明预测模型对比优选分析结果见表2。

由表2 可知，3 类模型的相对精度一致，但GM(1,1)模型的残差平方和最小，因此采用GM(1,1)对1号方案的建设项目投资进行预测。

表2 1号方案C1指标预测模型误差计算表Table 2 Error computation table of predication model

类似地，得到各方案各灰色指标的最优预测模型在各时间点的预测值见表3。

整理表1 及表3 中数据，得到不同时间点下的铁路路线优选决策的确定型决策矩阵。

表1 指标数据统计Table 1 Indicator data statistics table

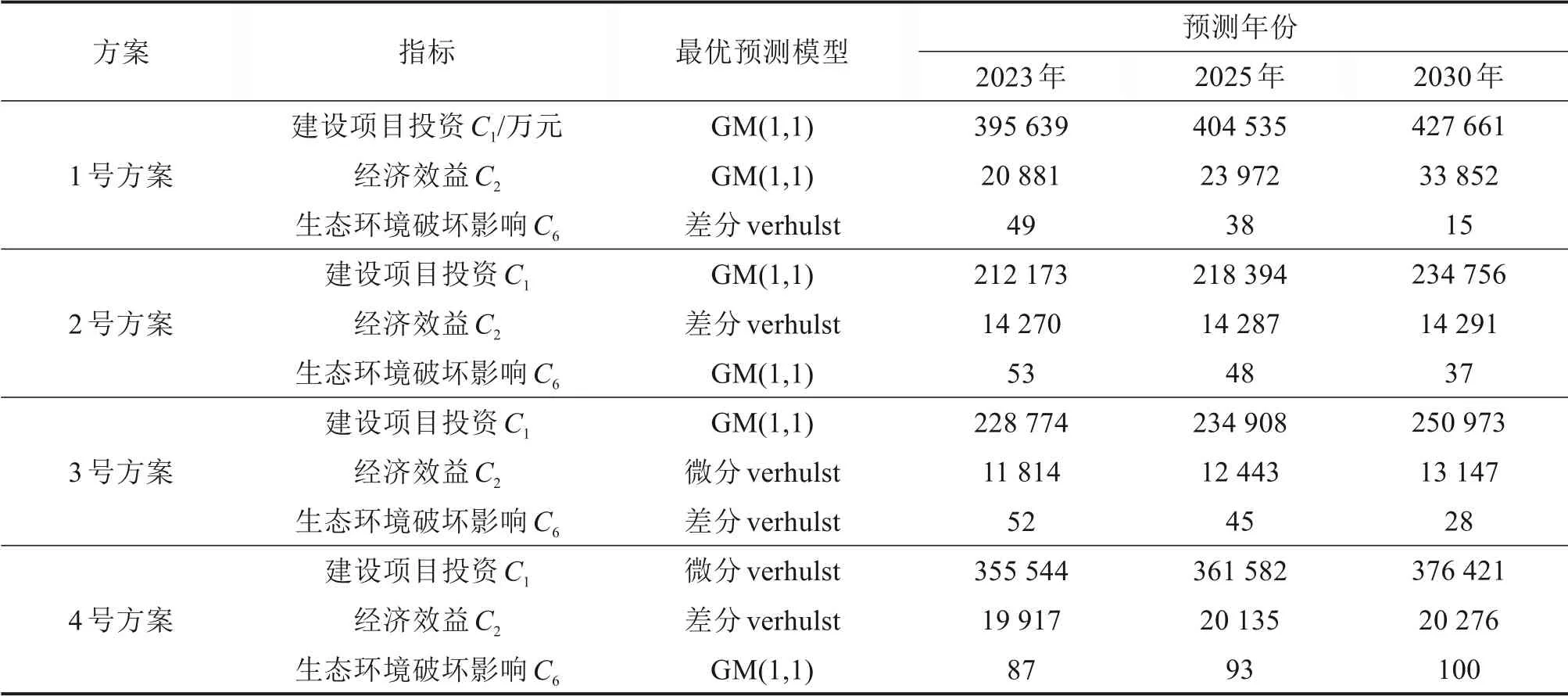
表3 各方案灰色指标白化预测值Table 3 Predicted value of gray index whitening for each scheme

2023年的决策矩阵：

2025年的决策矩阵：

2030年的决策矩阵：

根据式(6)～(9)对各指标进行规范化处理，得到2023 年，2025 年及2030 年铁路路线方案优选的决策属性矩阵U2023，U2025及U2030。

2.3 关联度值及效用前景值

根据矩阵U2023，U2025及U2030，铁路路线优选决策的正理想方案向量：

负理想方案向量：

根据式(11)及式(12)(分辨系数取0.5)，计算得到2023 年，2025 年及2030 年的正、负理想方案的关联度矩阵

利用式(13)～(14)得到不同时间点的正、负前景效用价值矩阵。

2023年正前景效用价值矩阵：

2023年负前景效用价值矩阵：

2025年正前景效用价值矩阵：

2025年负前景效用价值矩阵：

2030年正前景效用价值矩阵：

2030年负前景效用价值矩阵：

2.4 最优方案优选决策

综合前景值计算公式，各指标不定权重向量W=(w1,w2,…,wj,…,wm)，则 权 重处 理方式 如式(16)～(17)。为合理体现各指标的重要性，根据相关专家意见，单个指标权重的取值范围为0.05～0.3之间。各指标权重处理值为：

正前景效用权重处理值：

负前景效用权重处理值：

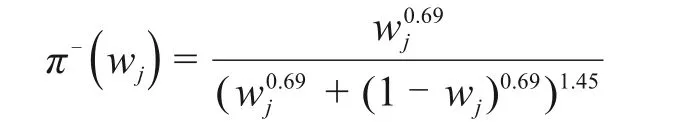
根据各方案综合前景值累加最大化原则，得到以不定权重为变量的约束非线性规划模型，目标函数为：

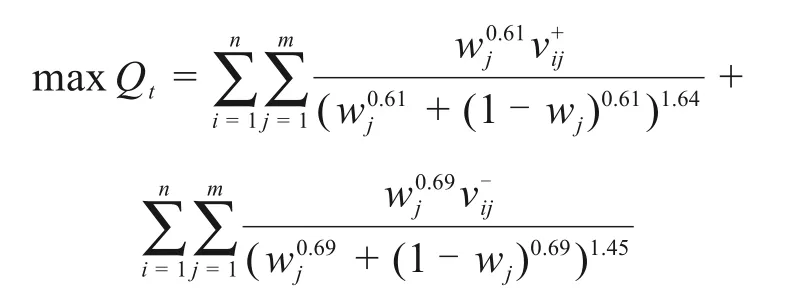
约束非线性规划模型的约束条件为：

计算得到各时间点累加综合前景值最大的权重向量：

2023 年：W2023= (0.05， 0.30， 0.05， 0.15，0.05，0.05，0.05，0.30)；

2025 年：W2025= (0.15， 0.30， 0.05， 0.05，0.05，0.05，0.05，0.30)；

2030 年：W2023= (0.05， 0.30， 0.05， 0.15，0.05，0.05，0.05，0.30)。

进而得到各方案综合前景值。

2023 年 时：Q1=-1.076 3，Q2=-0.110 9，Q3=-1.042 6，Q4=-0.033 6。

2025 年 时：Q1=-1.210 3，Q2=0.032 5，Q3=-1.080 9，Q4=0.004 4。

2030 年 时：Q1=-1.273 6，Q2=-0.103 2，Q3=-0.936 7，Q4=0.021 5。

2.5 结果分析

对不同时间点的不同方案综合前景值进行比较，2023年与2030年各方案优劣排序是一致的：4号方案＞2 号方案＞3 号方案＞1 号方案，但2025年各方案优劣排序为：2号方案＞4号方案＞3号方案＞1 号方案。说明在不同的时间点下，随着灰色指标数值的随时间的动态改变，方案之间的相对优势关系发生了很大变化，出现了最优方案的转移。其本质是因各备选方案随年份变化导致物价波动以及生态环境质量随人工改造在不同年份有所变化，而导致的决策局势的改变。此时，采用考虑时间变化因素的多灰色模型对比的累计前景理论进行建设时间不定情况下的铁路路线方案优选决策是必要的，其相对于如单一的累计前景理论分析等传统的确定型优选决策方法，确实更为适宜有效。

3 结论

1)构建了包括经济、技术等1级指标，建设项目投资，经济效益、正线长度等2级指标在内的铁路路线方案优选决策多级指标体系，并根据实际对指标进行了灵活调整。

2) 构建了考虑灰色指标影响的多灰色模型对比的累计前景理论模型。采用累计前景理论对铁路路线方案进行多目标优选决策，构建了以权重为变量，各方案累加综合前景值最大的约束非线性规划模型。模型充分考虑到方案建设时间点不确定时决策优选局势的动态变化，并考虑了决策者的非理性思维对优选决策的主观影响，模型构建科学，考虑问题全面合理。

3) 例证显示：在不同时间点下，各铁路路线方案之间的相对优势关系有很大变化，最终导致最优方案发生了转移。证明多灰色模型对比的累计前景理论对于此类随时间而发生局势变化的多目标优选决策问题具有较强的处理能力，相对确定型分析方法，分析过程更加贴近实际，分析结果也更为科学合理。