预应力混凝土梁工作机理及工程应用

刘世朋

摘 要：本文结合实际工程介绍预应力的基本概念及原理，预应力的等效荷载概念及线型设计，并通过截面应力法推导作用在混凝土梁上的预应力等效荷载，最后结合实际工程案例对上述原理加以应用。结果表明：预应力产生的截面弯矩与预应力中心线和混凝土截面形心线之间的距离成正比。当预应力中心线线型为抛物线时，弯矩呈抛物线分布;预应力中心线线型为直线时，弯矩呈直线分布。当预应力筋根数经过裂缝验算初步确定后，可以通过调整预应力筋的失高、预应力筋线型（即改变等效荷载）以及非预应力钢筋的面积来达到满足预应力梁施工阶段及使用阶段的验算。非预应力钢筋与预应力钢筋调整相结合，达到满足规范要求且安全经济的目的。

关键词：预应力梁，等效荷载，线型

Abstract： This paper introduces the basic concept and principle of prestressing， the concept of equivalent load of prestressing and linear design， and deduces the equivalent load of prestressing acting on the concrete beam through the section stress method. Finally， the above principle is applied combined with the actual engineering case. The results show that： （1） the section bending moment produced by prestress is directly proportional to the distance between the center line of prestress and the centroid of concrete section. When the center line of prestress is parabola， the bending moment is parabola; When the center line of prestress is a straight line， the bending moment is distributed in a straight line. （2） When the number of prestressed reinforcement is preliminarily determined by crack checking calculation， the checking calculation of prestressed beam in construction stage and service stage can be achieved by adjusting the height loss of prestressed reinforcement， the line type of prestressed reinforcement （i.e. changing the equivalent load） and the area of non prestressed reinforcement. The combination of non prestressed reinforcement and prestressed reinforcement can meet the requirements of the code and achieve the purpose of safety and economy.

Keywords： Prestressed beam; Equivalent load; Line type

一、預应力基本概念及原理

随着建筑水平的不断提高，人们对建筑的人性化和美观性要求也越来越高，要求混凝土不能出现裂缝，建筑层高也随着人们的审美要求而不断提高。对于大跨度结构，一般的混凝土梁已经很难满足上述要求，而预应力梁的出现解决了上述存在的问题，运用预应力技术，可以减轻结构自重，提高工程的安全性、稳定性与耐久性[1]。使建筑物具有更大的跨度和空间，满足多种建筑类型和建筑风格的需要。

普通混凝土的极限拉应变为0.1×10-3～0.15×10-3[2]，即每米只能拉长0.1 mm～0.15 mm，所以在使用荷载下，混凝土通常是带裂缝工作，对于不允许开裂的构件，受拉钢筋的应力只能到20～30 N/mm2，无法充分利用钢筋的强度。对于允许开裂的构件，通常当钢筋应力达到250 N/mm2，裂缝宽度已经达到0.2 mm～0.3 mm，此时构件耐久性降低，不宜用于高湿度或侵蚀性环境中。通常为满足变形和裂缝控制要求，可采用增大构件截面及配筋的方法或采用高强钢筋的方法。前者构件自重大，经济性较差;后者在使用荷载作用下，钢筋应力可达500～1000 N/mm2，但对应的裂缝宽度将非常大，因此普通混凝土中使用高强钢筋不能充分发挥其作用。

最理想的状态就是钢筋强度充分发挥（即钢筋拉应变较高），同时混凝土拉应变较低。对于普通混凝土结构，钢筋与混凝土一开始是变形协调的，无法达到这种理想状态，因此可采取的办法是在初始状态（即未施加使用荷载时）先给钢筋施加一个预拉力，使钢筋的初始应变就高于混凝土的初始应变，保证钢筋强度得到充分发挥，同时混凝土又能正常工作。

预应力就是在混凝土结构承受使用荷载之前的制作阶段预先对混凝土施加应力，此时钢筋产生拉应力与拉应变，混凝土产生压应力与压应变，即未施加使用荷载时，钢筋与混凝土已经产生了变形差（钢筋拉应变，混凝土压应变）。工程设计常需要用到的预应力相关知识及概念包括预应力混凝土强度等级、预应力强度比、等效荷载、预应力筋线型等。

（一）预应力混凝土强度等级

预应力混凝土结构设计规程规定，采用钢丝、钢绞线、热处理钢筋作为预应力钢筋时，混凝土强度等级不宜低于C40[3]。

（二）预应力强度比

预应力混凝土结构抗震设计规程3.2.8条规定了预应力强度比[4]：

λ=（f_py A_p h_p）/（f_py A_p h_p+f_y A_s h_s ）                       （1-1）

规程4.2.3条对预应力强度比规定：一级抗震等级时，λ≤0.60，二、三级抗震等级时，λ≤0.75。

（三）预应力等效荷载

张拉预应力筋对混凝土梁的作用，可用一组等效荷载来代替，等效荷载一般由两部分组成。

1. 预应力筋在锚固区对梁产生的压力Np。

2. 由曲线预应力筋曲率引起的、垂直于预应力筋束中心线的向上的分布力q[5]。

（四）预应力筋线型

预应力筋线型指预应力孔道（或无黏结预应力束）中心线的形状和位置，预应力筋线型一般由抛物线段和直线段组成，预应力筋线型与等效荷载形成的弯矩图形状一致。

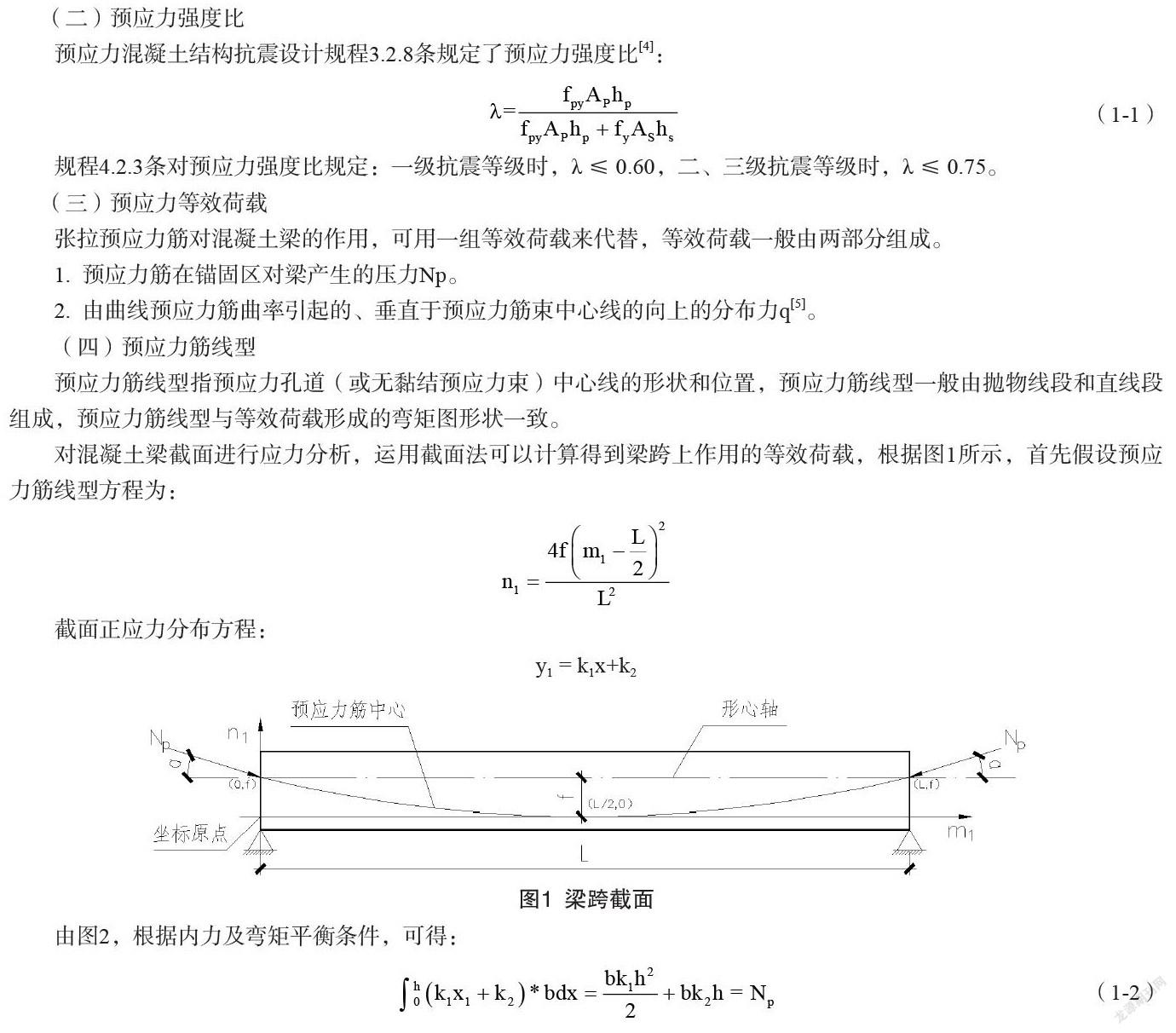
对混凝土梁截面进行应力分析，运用截面法可以计算得到梁跨上作用的等效荷载，根据图1所示，首先假设预应力筋线型方程为：

n_1=（4f（m_1-L/2）^2）/L^2

截面正应力分布方程：

y_1=k_1 x+k_2。

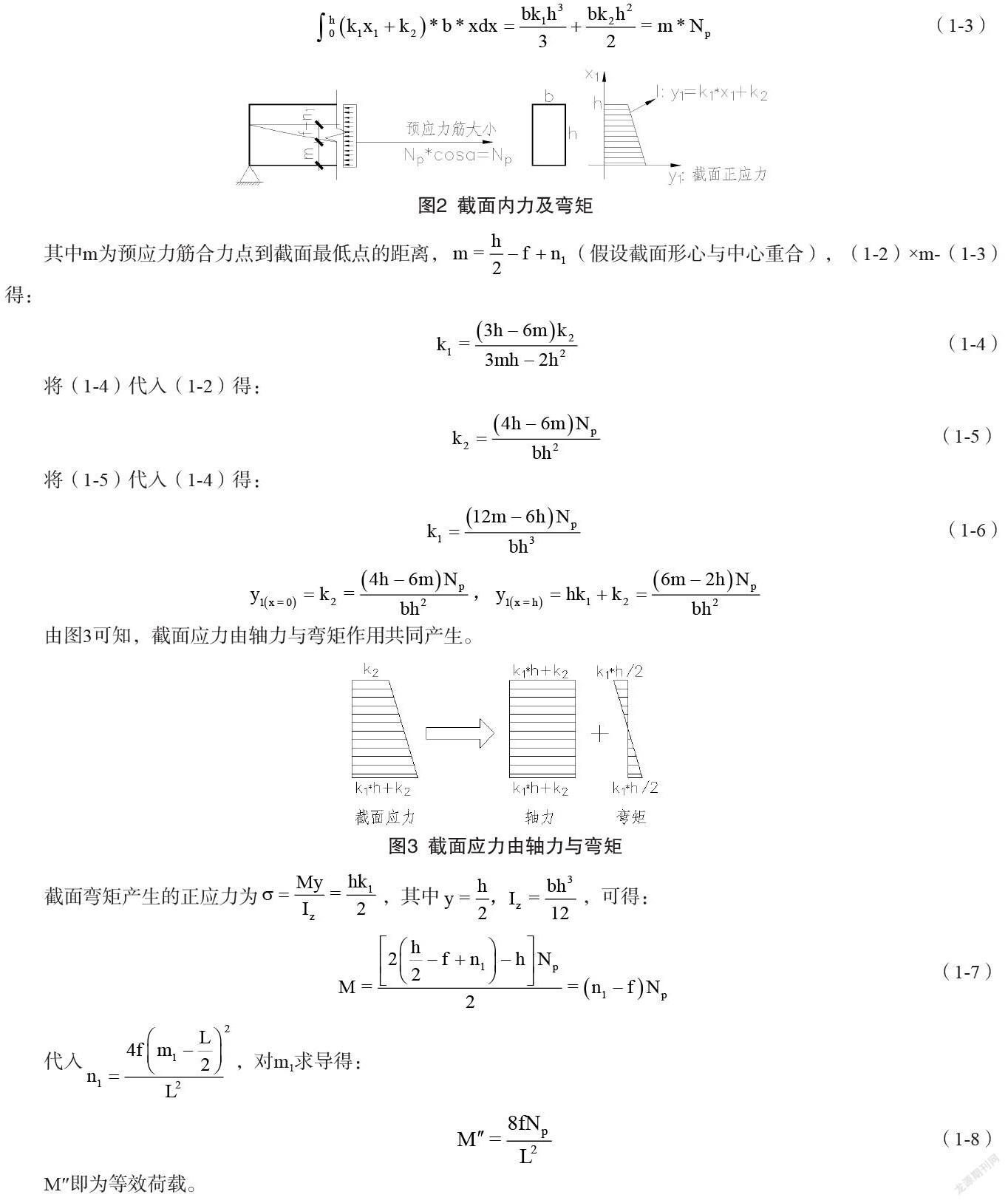
由图2，根据内力及弯矩平衡条件，可得：

∫_0^h▒〖（k_1 x_1 〗+k_2）*bdx=（bk_1 h^2）/2+bk_2 h=N_p                （1-2）

∫_0^h▒〖（k_1 x_1 〗+k_2）*b*xdx=（bk_1 h^3）/3+（bk_2 h^2）/2=m*N_p             （1-3）

其中m为预应力筋合力点到截面最低点的距离，m= h/2-f+n_1 （假设截面形心与中心重合），（1-2）×m-（1-3）得：

k_1=（（3h-6m） k_2）/（3mh-2h^2 ）                        （1-4）

将（1-4）代入（1-2）得：

k_2=（（4h-6m） N_p）/（bh^2 ）                         （1-5）

將（1-5）代入（1-4）得：

k_1=（（12m-6h） N_p）/（bh^3 ）                       （1-6）

y_（1（x=0））=k_2=（（4h-6m） N_p）/（bh^2 ）  ，y_（1（x=h））=hk_1 〖+k〗_2=（（6m-2h） N_p）/（bh^2 ）

由图3可知，截面应力由轴力与弯矩作用共同产生。

截面弯矩产生的正应力为σ=My/I_z =hk_1/2，其中y= h/2 〖，I〗_z=（bh^3）/12，可得：

M= （（2（h/2-f+n_1）-h） N_p）/2=（n_1-f） N_p              （1-7）

代入n_1=（4f（m_1-L/2）^2）/L^2 ，对m1求导得：

M^''=（8fN_p）/L^2                       （1-8）

M″即为等效荷载。

通过公式可以得出如下结论。

1. 预应力产生的截面弯矩与预应力中心线和混凝土截面形心线之间的距离成正比，当预应力筋线型为抛物线时，弯矩呈抛物线分布，预应力筋线型为直线时，弯矩呈直线分布。

2. 可以通过调整失高f来改变等效荷载值，或者改变预应力筋的数量来改变等效荷载值。

二、预应力计算内容

预应力计算内容分使用阶段和施工阶段两个阶段。

（一）使用阶段计算

使用阶段计算内容包括承载力计算和裂缝控制验算，其中承载力计算与普通混凝土梁计算一致，包括正截面与斜截面计算;裂缝控制验算，主要区分裂缝等级，一级要求不开裂，二级要求一般不裂;三级允许开裂，但要进行裂缝宽度验算以满足规范要求。

（二）施工阶段验算

使用阶段验算主要指构件运输、制作、吊装等施工阶段承载力、抗裂或裂缝宽度验算。

三、工程应用

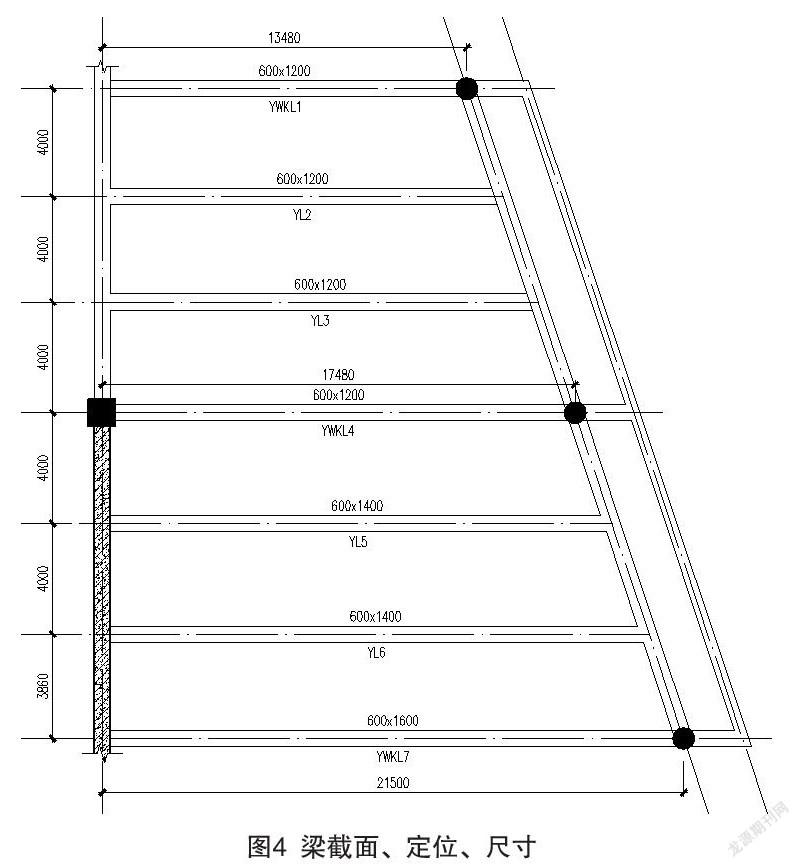
某工程大跨度屋面结构，屋面恒荷载为6 kN/m2，活荷载为3.5 kN/m2。最大跨度21.5 m，最小跨度13.48 m，采用单向混凝土梁布置方案，混凝土强度等级为C40，钢筋选用三级钢，单向大跨梁采用预应力梁以减小裂缝和梁高。梁截面、定位、尺寸如图4所示。

以图中YWKL4为例进行计算分析，梁计算跨度为17.480 m，按照梁跨度的1/15预估梁高，初步将梁截面选定为b×h = 600 mm×1200 mm。经计算，普通钢筋混凝土大跨度梁在结构荷载作用下，裂缝宽度已远远超出规范限值要求。需要在梁中添加预应力筋以满足裂缝限制要求。采用盈建科预应力计算模块，在框架梁中添加预应力筋进行模拟计算。

首先进行结构整体计算，得到预应力梁的非预应力钢筋面积，然后在预应力模块的选筋修改中更改非预应力筋为计算配筋;实配钢筋如图5所示。

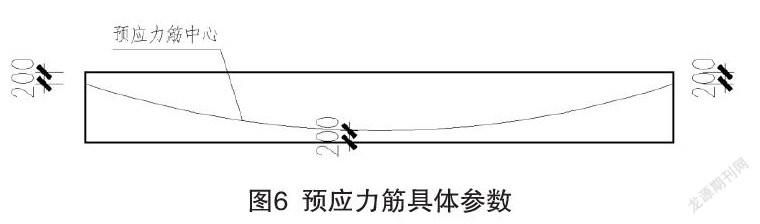
其次进行线型选择，由于作用在YWKL4上的荷载为均布线荷载，形成的弯矩由两端抛物线组成，因此线型选择由两端抛物线组成的短抛物线线型。然后进行预应力筋数量估算，根据无黏结预应力混凝土结构技术规程附录A，按照正截面裂缝控制验算要求，对预应力筋数量进行估算，首先计算有效预加力值，假定裂缝宽度限值为0.2 mm，根据表A.0.3-1求得混凝土名义拉应力限值为4.6 N/mm2。然后根据式A.0.2-1计算有效预加力值。再根据式A.0.1，估算预应力筋面积。最终确定预应力筋方案为2×7φ15.2，预应力筋线型两端及跨中位置与梁翼缘间的距离均假定为200 mm。具体参数如图6所示。

经计算，施工阶段梁右端梁底拉应力超限、Mcr/Mu大于1超限及跨中预应力强度比超过限值。

由于梁右端预应力筋失高（预应力筋重心与梁截面重心之间距离）较大，导致梁右端负弯矩较大，最终造成梁底拉应力超限，通过减小梁右端预应力筋失高以改变拉应力超限情况：将预应力筋中心线与梁上翼缘距离由200调整为300，然后再次进行计算分析，梁底拉应力已满足限值要求。

梁正截面弯矩承载力Mu与预应力大小无关，而预应力梁开裂弯矩Mcr与预加力大小有关，因此可通过减小预应力筋失高以减小开裂弯矩Mcr，从而使Mcr/Mu满足计算要求。将预应力筋中心线与梁下翼缘距离由200调整为300，然后再次進行计算分析，Mcr/Mu已满足计算要求。

由式1-1可知，预应力筋数量已经确定的前提下，通过适当增加跨中非预应力筋的数量可以满足预应力强度比的要求。

通过计算可知，预应力梁的设计包括两个方面，即预应力筋的设计和普通钢筋的设计，当预应力筋根数经过裂缝验算初步确定后，可以通过调整预应力筋的失高、预应力筋线型（即改变等效荷载）以及非预应力钢筋的面积来满足预应力梁施工阶段及使用阶段的验算。非预应力钢筋与预应力钢筋调整相结合，达到满足规范要求且安全经济的目的。

四、结论

预应力产生的截面弯矩与预应力中心线和混凝土截面形心线之间的距离成正比，当预应力中心线线型为抛物线时，弯矩呈抛物线分布;预应力中心线线型为直线时，弯矩呈直线分布。

当预应力筋根数经过裂缝验算初步确定后，可以通过调整预应力筋的失高、预应力筋线型（即改变等效荷载）以及非预应力钢筋的面积来达到满足预应力梁施工阶段及使用阶段的验算。非预应力钢筋与预应力钢筋调整相结合，达到满足规范要求且安全经济的目的。

参考文献：

[1]王菲.大跨度预应力梁优势分析探讨[J].价值工程， 2018，37（02）：102-103.

[2]GB50010-2010（2015年版），混凝土结构设计规范[S].北京：中国建筑工业出版社， 2015.

[3]JGJ92-2004，无黏结预应力混凝土结构技术规程[S].北京：中国建筑工业出版社， 2004.

[4]JGJ140-2004，预应力混凝土结构抗震设计规程[S].北京：中国建筑工业出版社， 2004.

[5]牛黎明.预应力等效荷载计算方法技术研究[J].交通科技， 2012，（05）：12-14.

雄安城市规划设计研究院有限公司，河北 071700