基于多功能网的最短路径查询算法

袁敏 孙更新 宾晟

摘要：在单一网络功能下节点间最短路径的研究基础上，提出基于多功能网的最短路径查询问题，给出一种基于贪心策略的查询算法来查询节点间在不同网络功能下的最短路径。利用多功能网对山东半岛城市群进行建模，分别查询城市群网络实现经济和信息两种不同功能时城市间的最短路径，并计算分析。研究结果表明，查询节点间在不同网络功能下的最短路径对于挖掘复杂系统不同功能间的潜在联系具有一定的现实意义。

关键词：多功能网;最短路径查询算法;中心性;山东半岛城市群

中图分类号：N95

文献标志码：A

收稿日期：2020-11-02

基金项目：

教育部人文社会科学研究青年项目（批准号：15YJC860001）资助;山东省自然基金面上项目（批准号：ZR2017MG011）资助;山东省社会科学规划项目（批准号：17CHLJ16）资助。

通信作者：

孙更新，男，博士，副教授，主要研究方向为大数据分析、数据挖掘、复杂网络。E-mail：sungengxin@qdu.edu.cn

挖掘复杂系统不同功能间的潜在联系，实现系统各种功能间的优势互补，对于优化系统结构，促进系统发展具有重要意义。复杂网络是研究复杂系统的重要工具之一，但以往的复杂网络模型如随机图[1]、二分图[2-3]、层次网络[4-5]和多子网复合复杂网络模型[6-7]等均将系统中的实体表示为节点，将实体间的相互作用表示为连边，拓扑结构相对固定，功能相对单一，而多功能网[8]可以充分利用并动态地选择节点的属性，依据映射规则来确定节点间的相互作用，实现不同的网络结构和功能。最短路径查询[9-11]是图论中的一个经典问题，旨在寻找图中两个节点间的最短路径，其在复杂网络领域有重要的应用，如网络直径、平均最短路径长度、紧密中心性和介数中心性等复杂网络分析中重要的特征度量，均可以在最短路径查询的基础上进一步计算获得。图论中回答最短路径查询的方法主要有两类，第一类方法不对原始数据图进行任何的预处理操作，此类方法的代表性算法有BFS算法、Dijstra算法[12-13]、Floyd算法[14-15]和A*算法[16]。第二类方法首先对原始数据图构建相应的索引，然后在相应的索引上进行最短路径查询操作，此类方法的代表性算法有IS_LABEL算法[17]和PLL算法[18]。但这些方法均无法查询节点间在不同网络功能下的最短路径。综上，本文提出基于多功能网的最短路径查询，给出MFCNSPQ算法来查询节点间在不同网络功能下的最短路径，并参考文献[19-21]，对山东半岛城市群进行建模、查询与分析。

1 多功能网

多功能网认为实体间的相互作用与实体的特征属性有关，利用节点来表示复杂系统中的实体，节点以特征属性向量的形式表示，通过动态地选择特征属性集，依据相应的特征属性集映射函数来确定节点间的关联，进而实现特定的网络功能。该模型使用三元组MFCN=V，P，F来表示：

（1）V=∪|V|i=1vi是多功能网的节点集合;

（2）P=∪|P|h=1Ph是多功能网的特征属性集合，domP=∪Ph∈Pdom（Ph）是特征属性集P的值域集合，节点vi在Ph下的取值为pih∈domPh，pi=（pi1，pi2，…，pih，…，piP）是节点vi的在特征属性集P下的向量表示形式;

（3）Fvi，vj=ξ（f1，f2，…，fh，…，ft）是多功能网基于所选择的特征属性集P*（P*P）的特征属性集映射函数，节点vi，vj间基于特征属性集P*建立的關联通过其实现，其中t≤P，fh是特征属性Ph对应的特征属性映射函数。

节点数量为V，具有P个特征属性的多功能网，可用V×P的矩阵描述：

2 基于多功能网的最短路径查询

2.1 基本概念

定义1 基于特征属性集映射函数F的路径。对多功能网MFCN=V，P，F，选择不同的特征属性集，其映射函数不同，节点间的相互作用不同，进而使得节点间的路径不同。给定起始节点vs和目标节点vt（vt≠vs），若有节点序列l=vs，…，vk，vk+1，…，vt，其中vk，vk+1∈l在特征属性集映射函数F下均存在关联，则称l为由节点vs到vt的基于特征属性集映射函数F的路径，简记为基于F的路径。

定义2 基于特征属性集映射函数F的物理路径长度。若l为由节点vs到vt的基于F的路径，那么节点vs到vt的基于特征属性集映射函数F的物理路径长度，简记为基于F的物理路径长度为

lFvs，vt=∑vk，vk+1∈lσ（Fvk，vk+1）（1）

其中，σ为函数，在特征属性集映射函数F下，当节点vi和vj存在关联时，有σFvi，vj=1，否则σFvi，vj=0。

定义3 基于特征属性集映射函数F的最短物理路径。设l为由节点vs到vt的基于F的路径，若多功能网中找不到一条由节点vs到vt的基于F的路径w使得wFvs，vt<lFvs，vt，那么称l为由节点vs到vt的基于特征属性集映射函数F的最短物理路径，简记为基于F的最短物理路径。

定义4 基于特征属性集映射函数F的物理距离。若l为由节点vs到vt的基于F的最短物理路径，那么lFvs，vt为节点vs到vt的基于特征属性集映射函数F的物理距离，简记为基于F的物理距离。

2.2 查询算法

基于多功能网的最短路径查询的形式定义为Q=（vs，vt），其中vs为起始节点，vt为目标节点，则多功能网上基于特征属性集映射函数最短路径查询问题（MFCNSPQ）定义如下：

输入：多功能网MFCN，最短路径查询Q;

输出：节点vs到vt的基于F的全部最短物理路径。

采用贪心的思想解决MFCNSPQ问题，算法具体步骤如下：

Step 1 利用特征属性集映射函数F对节点vs和vt进行运算，得到返回值Fvs，vt，判断Fvs，vt是否满足映射规则，若满足，则l=vs，vt为vs到vt的基于F的最短物理路径，算法结束，否则执行Step 2;

Step 2 利用特征属性集映射函数F对节点vs和多功能网中除节点vt外的其他节点逐一运算，返回值满足映射规则的节点组成集合S，更新集合S中节点的前置节点为vs，利用特征属性集映射函数F对集合S中节点和节点vt逐一运算，返回值满足映射规则的节点为节点vt的前置节点，若节点vt的前置节点信息不为空，则根据节点的前置节点信息得到节点vs到vt的基于F的全部最短物理路径，算法结束，否则执行Step 3;

Step 3 利用特征属性集映射函数F对集合S中节点和多功能网中除节点vs和vt外还未加入过集合S节点逐一运算，返回值满足映射规则的节点组成新的集合S，更新集合S中节点的前置节点信息，利用特征属性集映射函数F对集合S中节点和节点vt逐一运算，返回值满足映射规则的节点为节点vt的前置节点，若节点vt的前置节点信息不为空，则根据节点的前置节点信息得到节点vs到vt的基于F的最短物理路径，算法结束，否则重复执行Step 3，直到节点vt的前置节点信息不为空，找到节点vs到vt的基于F的全部最短物理路径。

由于MFCNSPQ算法总是先寻找距离起始节点vs为k的所有节点，再寻找距离vs为k+1的所有节点，并记录查询过程中节点的全部前置节点信息，因此通过MFCNSPQ算法一定能找到节点vs到vt的基于F的全部最短物理路径。通过多功能网一个实例对MFCNSPQ算法过程进行解释。实例节点集V=∑7i=1vi，特征属性集P=P1，P2，P3，P4，P5，P6，节点vi的特征属性向量形式pi=（pi1，pi2，pi3，pi4，pi5，pi6）。该实例被描述为一个7×6阶的矩阵：

P1P2P3P4P5P6

v1v2v3v4v5v6v7100000

110000

101100

011010

000101

000011

000000

查询节点v1到v6的基于F的最短物理路径，其中F为特征属性集P*=P对应的特征属性集映射函数，利用特征属性集映射函数F对节点vi和vj进行运算，Fvi，vj=pi·pj，返回值Fvi，vj1时，满足映射规则，节点vi和vj在特征属性集映射函数F下存在关联。具体步骤如下：

Step 1 利用特征属性集映射函数F对节点v1和v6进行运算，得到返回值Fv1，v6=0，不满足映射规则，执行Step 2;

Step 2 利用特征属性集映射函数用F对节点v1和节点v2，v3，v4，v5，v7逐一运算，有Fv1，v2和Fv1，v3满足映射规则，于是集合S={v2，v3}，更新节点v2和v3的前置节点信息为v1，利用特征属性集映射函数F对节点v2、v3和节点v6逐一运算，Fv2，v6和Fv3，v6均不满足映射规则，执行Step 3;

Step 3 利用特征属性集映射函数用F对节点v2、v3和节点v4、v5、v7逐一运算，有Fv2，v4、Fv3，v4和Fv3，v5满足映射规则，于是S={v4，v5}，更新节点v4的前置节点信息为v2和v3，节点v5的前置节点信息为v3，利用特征属性集映射函数F对节点v4、v5和节点v6逐一运算，Fv4，v6和Fv5，v6均满足映射规则，更新节点v6的前置節点信息为v4和v5，此时v6的前置节点信息不为空，根据所记录的前置节点信息，得到节点v1到v6的基于F的最短物理路径为l1=v1，v2，v4，v6，l2=v1，v3，v4，v6和l3=v1，v3，v5，v6。

3 实验

3.1 建模

在《山东半岛城市群发展规划（2016—2030年）》中提出以17个地级市：济南、青岛、淄博、枣庄、东营、烟台、潍坊、济宁、泰安、威海、日照、莱芜（2019年1月正式撤销）、临沂、德州、聊城、滨州、菏泽共同组成山东半岛城市群。考虑本文从经济和信息角度出发讨论的山东半岛城市群网络所需数据信息以及数据的时效性和完整性，收集并处理了山东半岛城市群中各城市的2018年的年末人口数、地区生产总值、里程和信息关注度的信息，数据来源于《山东统计年鉴2019》、百度指数20180101—20181231和百度地图。

以城市为节点，基于多功能网的山东半岛城市群网络可用17×4阶的矩阵描述：

P1 P2 P3P4

v1v2v17

655.97856.6（0，352，…，243）（0，691，…，452）

817.812 001.5（325，0，…，529）（547，0，…，303）

1 025.43078.8（243，529，…，0）（235，210，…，0）

其中，节点集V=∑17i=1vi，特征属性集P={P1，P2，P3，P4}，P1为城市年末人口数，P2为城市生产总值，P3为城市群中某城市与其他城市间的最短公路里程，P4为基于百度指数整体日均值的城市群中某城市对其他城市的搜索指数。城市节点vi的特征属性向量形式pi=（pi1，pi2，pi3，pi4），pi1为城市vi的年末人口数，pi2为城市vi的生产总值，pi3=（li1，li2，…，lij，…，li17），lij为城市vi的与城市vj间的最短公路里程，j=i时，lij=0，pi4=（qi1，qi2，…，qij，…，qi17），qij为基于百度指数整体日均值的城市vi对城市vj的搜索指数，在此不考虑城市对自身的搜索指数，即j=i时，qij=0。

通常认为城市间的联系密切程度与城市间的相互吸引力有关，根据引力模型及其改进模型，城市间的引力强度与其质量水平呈正相关，与其距离呈负相关。利用城市年末人口数和生产总值表示城市经济质量水平，城市间的最短公路里程表示城市间的距离，选择特征属性集P*=P1，P2，P3，相应的特征属性集映射函数为

FEcovi，vj=kij× pi1pi2×pj1pj2D2ij（2）

通过FEco（vi，vj）可建立城市vi和vj间的经济联系，其中，kij=pi2/（pi2+pj2）为城市vi在城市vi与vj经济发展联系中的贡献率，Dij=ej·pi3，ej为第j个分量值为1的1×17阶的单位向量。

由于基于百度指数获取的关注度数据覆盖面广泛，可以作为一种较为可信的数据用以表征城市间的信息流特征，选择特征属性集P*={P4}，相应的特征属性集映射函数为

FInforvi，vj=ej·pi4（3）

通过FInforvi，vj可建立城市vi和vj间的信息联系，其中，ej同上。

3.2 分析

从算法的适用场景对基于多功能网的最短路经查询算法与其他最短路径查询算法进行对比分析，如表1，其中静态网络指网络结构固定，动态网络指根据用户的不同功能需求，网络结构不同。MFCNSPQ算法通过改变特征属性集映射函数来改变网络结构，进而实现动态网络上的最短路经查询，相较于其他算法适用场景更广。

紧密中心性和介数中心性是复杂网络分析中与节点间最短路径相关的两个重要的中心性度量指标。多功能网中节点基于特征属性集映射函数F的物理紧密中心性（简记为基于F的物理紧密中心性）

CCFvi=minvk∈V∑vj∈VlFvk，vj/∑vj∈VlFvi，vj（4）

其中，minvk∈V∑vj∈VlFvk，vj为多功能网中所有节点与其他节点间基于F的物理距离之和中的最小值，∑vj∈VlFvi，vj为节点vi与其他节点间基于F的物理距离之和。当任意一对节点间不存在基于F的最短物理路径时，节点间基于F的物理距离记为SymboleB@，若分子或分母为SymboleB@，令CCFvi=0，则0≤CCFvi≤ 1。节点vi与其他节点间基于F的物理距离越近，CCFvi越接近1，节点vi基于F的物理紧密中心性越高。节点vi与vj间基于F的最短物理路径存在方向时，可以分为基于F的出物理紧密中心性和基于F的入物理紧密中心性。

多功能网中节点基于特征属性集映射函数F的物理介数中心性（简记为基于F的物理介数中心性）定义为

BCFvi=∑vs≠vi≠vt∈VδFvs，vt（vi）/δFvs，vt（5）

其中，δFvs，vt为节点vs与vt间基于F的最短物理路径的条数，δFvs，vt（vi）为节点vs与vt间基于F的最短物理路径经过节点vi的条数。节点间基于F的最短物理路径中经过节点vi的条数越多，BCFvi越大，节点vi基于F的物理介数中心性越高。

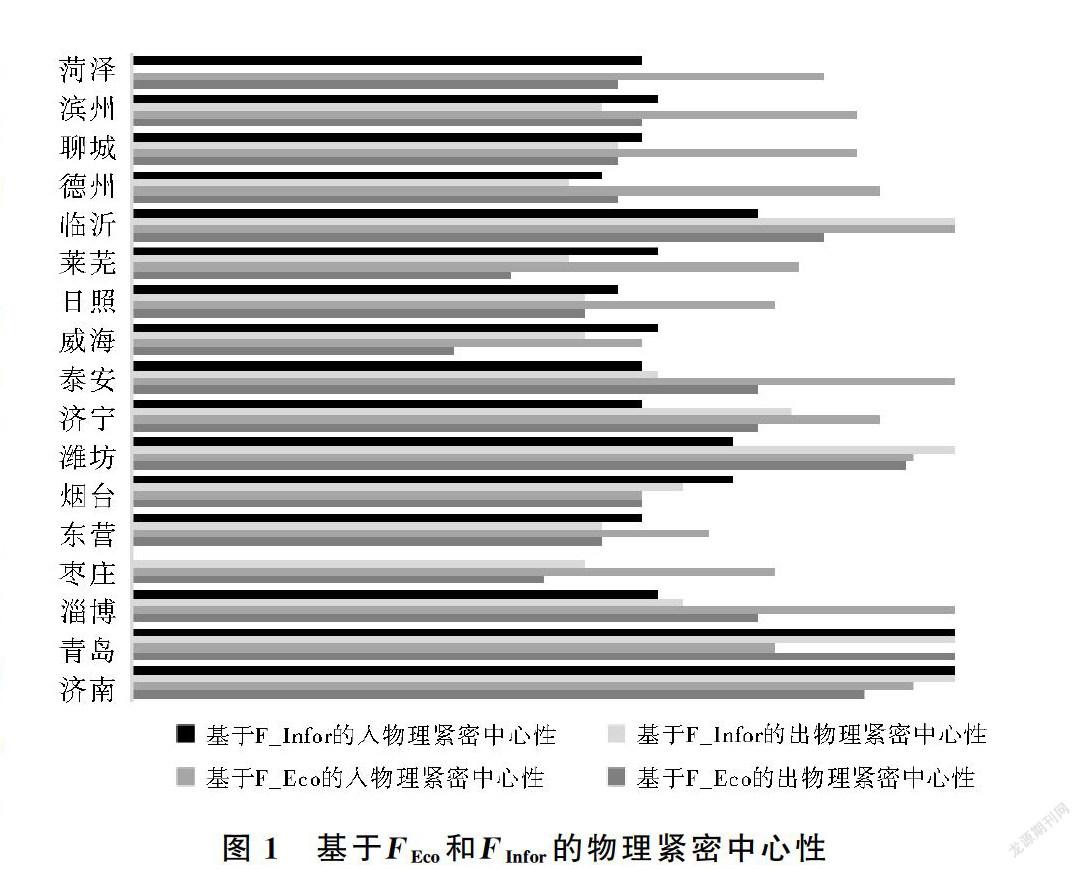
利用MFCNSPQ算法查询山东半岛城市群网络中所有城市节点间基于FEco和FInfor的最短物理路径，根据式（4）对各城市节点基于FEco和FInfor的出物理紧密中心性进行计算，结果如图1。从出物理紧密中心性来看，济南、青岛、潍坊和临沂基于FEco和FInfor的物理紧密中心性均明显高于其他城市，能与其他城市更快的主动产生经济和信息联系，具有很强经济和信息辐射能力。从入物理紧密中心性来看，淄博、泰安和临沂基于FEco的入物理紧密中心性较高，其次为济南、潍坊、济宁和德州，这些城市更容易受到其他城市的影响，具有较强的经济资源整合能力;济南和青岛基于FInfor的入物理紧密中心性远高于其他城市，是城市群中信息集聚的中心。

根据式（5）对各城市节点基于FEco和FInfor的物理介数中心性进行计算，结果如图2。山东半岛城市群网络中城市节点基于FEco和FInfor的物理介数中心性两极分化明显。基于FEco的物理介数中心性均值为911，高于这一均值的城市有潍坊、泰安、济南、临沂、青岛、烟台、淄博和济宁，其中，潍坊位于城市群中部作为重要的交通枢纽，其基于FEco的物理介数中心性远高于其他城市，是城市群城市间经济联系中的重要纽带;基于FInfor的物理介数中心性均值为789，高于这一均值的城市有济南、青岛、潍坊和临沂，其中，济南和青岛基于FInfor的物理介数中心性远高于其他城市，对城市群城市间信息流动具有很强控制能力。

综上，山东半岛城市群的经济和信息空间基本呈现一致性且均表现为多中心格局，济南、青岛、潍坊和临沂是带动城市群经济和信息发展的重要力量，淄博、烟台、济宁和泰安在中心城市的辐射带动下也表现出了一定的发展潜力，而枣庄和日照等城市在经济和信息空间中则处于边缘地位。建议未来充分利用经济和信息建設的相互促进作用，在继续发展和扩大中心城市辐射能力的基础上，重点培育潜力城市，对边缘城市产生新的带动作用，从而实现山东半岛城市群的协调发展。

4 结论

本文研究了基于多功能网的最短路径查询问题。利用节点在不同特征属性集下的相互作用，查询节点间基于不同特征属性集映射函数的全部最短物理路径。提出了MFCNSPQ算法并分析了其有效性，相较于其他最短路径查询算法，MFCNSPQ算法具有更广的适用场景。结合社会科学领域知识，从经济和信息角度对山东半岛城市群网络进行了查询与中心性分析，结合分析结果为区域规划和政策部署提供了建议。由于本文在进行查询时，并未考虑节点间的关联权值，这可能会导致部分网络信息的损失，因此在以后的研究中基于多功能网的考虑节点间关联权值的最短路径查询问题是重要的方向。

参考文献

[1]LEIFELD P，CRANMER S J. A theoretical and empirical comparison of the temporal exponential random graph model and the stochastic actor-oriented model[J]. Radiochimica Acta， 2015，94（2）：679-682.

[2]吴亚晶，张鹏，狄增如，等. 二分网络研究[J]. 复杂系统与复杂性科学，2010，7（1）：1-12.

[3]MATTHIEU L，CLEMENCE M，NATHALIE D V. Basic notions for the analysis of large two-mode networks[J]. Social Networks， 2008，30（1）：31-48.

[4]KURANT M，THIRAN P. Layered complex networks[J]. Physical Review Letters，2006，96（13）：138701.

[5]KURANT M， THIRAN P， HAGMANN P. Error and attack tolerance of layered complex networks[J]. Physical Review E， 2007，76（2）：026103.

[6]邵峰晶，孫仁诚，李淑静，等. 多子网复合复杂网络及其运算研究[J]. 复杂系统与复杂性科学，2012， 9（4）：20-25.

[7]隋毅，邵峰晶，孙仁诚，等. 基于向量空间的多子网复合复杂网络模型动态组网运算的形式描述[J]. 软件学报， 2015， 26（8）：2007-2019.

[8]钟丽君，宾晟，袁敏，等. 多功能复杂网络模型及其应用[J]. 复杂系统与复杂性科学， 2019，16（2）：31-40.

[9]XIAO Y， WU W， PEI J， et al. Efficiently indexing shortest paths by exploiting symmetry in graphs[C]// International Conference on Extending Database Technology. New York，2009：439-504.

[10] TREYTAKOV K， ARMAS-CERVANTES A， VILO J， et al. Fast fully dynamic landmark-based estimation of shortest path distances in very large graphs[C]// Acm Conference on Information & Knowledge Management. New York， 2011：1785-1794.

[11] 李忠飞，杨雅君，王鑫.基于规则的最短路径查询算法[J].软件学报，2019，30（3）：515-536.

[12] PHILANI B， RANDHIR R. Development of an optimal state transition graph for trajectory optimisation of dynamic systems by application of Dijkstra's algorithm[J]. Computers & Chemical Engineering， 2019， 125：569-586.

[13] 王树西，李安渝.Dijkstra算法中的多邻接点与多条最短路径问题[J].计算机科学，2014，41（6）：217-224.

[14] 左秀峰，沈万杰.基于Floyd算法的多重最短路问题的改进算法[J].计算机科学，2017，44（5）：232-234+267.

[15] 卢立果，刘立越，鲁铁定，等.一种改进的Floyd算法[J].东华理工大学学报（自然科学版），2019，42（1）：78-81.

[16] KANG N K， SON H J， LEE S H. Modified A-star algorithm for modular plant land transportation[J]. Journal of Mechanical Science and Technology， 2018， 32（12）：5563-5571.

[17] FU W C， WU H， CHENG J， et al. IS-LABEL： An independent-set based labeling scheme for point-to-point distance querying on large graphs[J]. Proceedings of the Vldb Endowment， 2012， 6（6）. doi：10.14778/2536336.2536346

[18] TAKUYA A，YOICHI I，YUICHI Y. Fast exact shortest-path distance queries on large networks by pruned landmark labeling[C].//Proceedings of the 2013 ACM SIGMOD International Conference on Management of Data，NewYork，2013：349-360.

[19] 马学广，唐承辉. 基于功能性联系的山东半岛城市群空间范围划定实证研究[J]. 经济地理， 2020， 40（5）：106-117.

[20] 刘晓明，孙毅，秦梦. 山东经济增长中的结构调整效应分解与路径分析—基于新旧动能转换的视角[J]. 青岛大学学报（自然科学版）， 2020， 33（1）：91-98.

[21] 王振波，杨励雅，梁龙武，等.山东半岛城市群交通网络载流能力评估与优化研究[J]. 地球信息科学学报， 2017， 19（6）：808-817.

Shortest Path Query Algorithm Based on Multi-functional Network Model

YUAN Min， SUN Geng-xin， BIN Sheng

（School of Data Science and Software Engineering， Qingdao University， Qingdao 266071， China）

Abstract：

The shortest path between nodes under single network function has been widely concerned in the existing research. On this basis， the shortest path query problem based on multi-functional network model is proposed， and a query algorithm based on greedy strategy is proposed to query the shortest path between nodes under different network functions. In the experiment， the multi-functional network model is used to model the urban agglomeration of Shandong Peninsula， and the shortest paths between cities when the urban agglomeration network realizes two different functions of economy and information are queried and calculated and analyzed. The result shows that querying the shortest paths between nodes under different network functions has certain practical significance for mining the potential connections between different functions of complex systems.

Keywords：

multi-functional complex network model; shortest path query algorithm; centrality; Shandong Peninsula urban agglomeration