基于IAFS算法的毫米波大规模MIMO混合预编码方法

陈浩椅，李光球，李辉

（杭州电子科技大学通信工程学院，浙江 杭州 310016）

1 引言

毫米波大规模多输入多输出（multiple input multiple output，MIMO）混合预编码器包括基带数字预编码器和射频模拟预编码器两个组成部分，因具有较好的性能与实现复杂度折中，是5G移动通信系统中的一项关键技术[1]，其中采用移相器结构射频模拟编码的全连接或部分连接混合预编码设计为目前的研究热点[2-3]。全连接混合预编码的设计方法有正交匹配追踪 （orthogonal matching pursuit，OMP）算法[4]、采用低分辨率量化移相器的深度学习法[5]、字典约束法[6]以及采用最小均方误差准则的混合预编码方法[7]等。

由于全连接结构混合预编码器的每个射频链路均与所有的移相器相连，所以实现复杂。为降低实现复杂度，提出了硬件成本低、能量效率高、具有较好性能与实现复杂度折中的部分连接结构混合预编码器[8-11]。参考文献[8]提出一种基于串行干扰消除（successive inter+erence cancellation，SIC）的混合预编码方法，将混合预编码矩阵设计问题转化为子天线阵列的优化问题，其特点是将其中的数字预编码矩阵设计为对角阵，适用于输入的数据流数与发送的射频链路数相等的应用场景，并具有较好的能量效率。参考文献[9]针对高信噪比（signal-to-noise ratio，SNR）与低SNR条件分别提出了两种混合预编码矩阵设计方法, 均能获得不错的频谱效率性能。参考文献[10-11]假定给定了模拟预编码矩阵，将模拟预编码矩阵与信道矩阵的乘积定义为等效矩阵，数字预编码矩阵在等效矩阵的基础上进行设计。参考文献[10]提出了一种基于频谱效率最大化准则和鸟群算法的混合预编码方法，该方法将混合预编码的设计转为优化问题，用鸟群算法进行寻优，获取了较好的频谱效率与误码率性能。参考文献[11]直接利用信道矩阵的相位信息设计模拟预编码矩阵，通过对等效矩阵进行奇异值分解设计数字预编码矩阵，避免了复杂的迭代或者搜索，具有实现复杂度低的特点。

综上，全连接或部分连接混合预编码的设计大多表现为基于频谱效率或能量效率准则的寻优问题。人工鱼群（arti+icial +ish swarm，AFS）算法的全局性寻优能力较强，对算法的各个参量的取值不敏感，对目标函数的搜索空间与初值无特殊的限制[12-13]。但是传统的AFS算法存在算法收敛速度较慢的缺点[13]，为此提出了改进的人工鱼群（improve2 arti+icial +ish swarm，IAFS）算法，与传统 AFS算法的区别在于算法初期采用大步长、后期采用小步长，能够加快算法的收敛速度和提升算法性能。

本文借鉴参考文献[10-11]的设计思想，尝试将IAFS算法应用于毫米波大规模MIMO系统，提出一种基于 IAFS算法的部分连接结构混合预编码方法。本文使用的符号说明如下：( ·)T与 (· )H分别代表矩阵的转置与共轭转置，Am,n表示矩阵A的第(m,n)个元素，||·||是 L2 范数,E(·)代表求期望。

2 系统模型

考虑平坦衰落信道上采用部分连接混合预编码方法的毫米波大规模MIMO系统，如图1所示。假定如下内容。

· 发射端配备有Nt根发射天线、个射频链路及与其相连接的基带数字预编码器与射频模拟预编码器，基带与射频预编码矩阵分别为Nt×维的FRF与×Ns维的FBB。

· 接收端配备有Nr根接收天线、个射频链路及与其相连接的数字与模拟合并器，数字合并矩阵与模拟合并矩阵分别为×Ns维的WBB与Nr×维的WRF。

·Ns个输入数据流先进行编码矩阵为FBB的数字预编码，再进行编码矩阵为FRF的模拟预编码，之后由Nt根发射天线发射至信道。Nr根接收天线上的信号依次经模拟、数字合并处理后得到Ns个输出数据流。

·Ns≤≤Nt，Ns≤≤Nr，发射端移相器数NPS=Nt。

· 信道矩阵为Nr×Nt维的H。

本文采用拓展的Saleh-Valenzuela毫米波信道模型[14]：

其中，Ncl与Nray分别代表群簇数目和每个群簇的路径数，δi,l表示第i个群簇的第l条散射波束路径的增益，服从高斯分布。φi,l∈ [ 0,2π]、θi,l∈[0,2π]分别表示第i个群簇的第l条路径的到达角和离开角，αMS(φi,l)和αBS(θi,l)分别表示用户天线阵列响应矢量和基站天线阵列响应矢量。假定收/发天线阵列采用均匀线性阵列，αMS(φi,l)和αBS(θi,l)可表示为：

其中，k表示电磁波波长，d表示天线之间的距离，假定d=k2。

假定发射端具有理想的信道状态信息（channel state in+ormation，CSI），则经合并矩阵为WRF、WBB的模拟与数字合并后的接收信号为[4]：

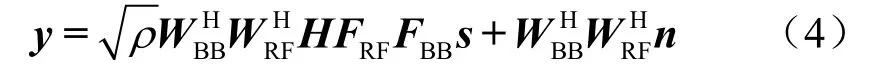
其中，ρ为平均接收功率，n∈CNr×1为加性高斯白噪声矢量，服从复高斯分布，即n∈CN(0,σ2INr)，σ2为噪声方差，INr是Nr×Nr维的单位阵。

采用与参考文献[4]相同的假定，如下。

· 信道矩阵H满足

·FRF与FBB满足功率限制

·FRF的元素满足恒模约束，即其 中 ， 1 ≤m≤Nt，

· 发送信号s∈CNs×1满足其中，INs是Ns×Ns维的单位阵。

部分连接结构的模拟预编码矩阵FRF可具有下面特殊的块对角矩阵形式[8]：

图1所示系统的频谱效率R可表示为[4]：

图1 采用部分连接混合预编码的毫米波大规模MIMO系统

采用参考文献[8]的能耗模型，图1所示系统的能量效率η可表示为：

其中，Pt为总发射功率，PPS为单个移相器功率，PRF为单个射频链路功率。

3 基于IAFS的混合预编码方法

3.1 问题描述

采用频谱效率最大化准则设计图1所示系统的混合预编码矩阵，为了简化问题，只考虑发送端的数字与模拟预编码矩阵的设计，此时系统的频谱效率可以表示为[14]：

设计FBB与FRF，使式（8）的频谱效率最大化是本文的目标，要直接求解将非常棘手。此外，FBB要满足功率限制，FRF要满足恒模限制与式（5）的块对角化形式。式（8）的优化问题是一个多元素非凸优化问题，目前尚无通用的解决方案[4]，下面尝试用IAFS算法进行求解。

3.2 求解方案

将 IAFS算法应用于混合预编码设计的具体思路如下。

（1）假定模拟预编码FRF已知，令信道矩阵H与FRF的乘积作为一个等效信道矩阵Heq。

（2）为了降低实现复杂度，可以将FBB设计为等效矩阵的最大比传输预编码矩阵[15]：

（3）通过前两个步骤可知，整个混合预编码设计只需设计一个未知变量FRF，可将式（8）进行转化，建立下面基于频谱效率的目标函数Y：

（4）利用IAFS算法优化目标函数Y完成混合预编码设计。

式（9）中的F为FRF的候选解集合。通过步骤（1）与（2）可将多元素的优化问题转化为单一元素的优化问题；由上述设计步骤可知 IAFS方法所设计的FBB无参考文献[8]的对角阵的限制，所以对于不等于Ns的系统，IAFS方法也同样适用。

而式（9）的求解需寻找到一个最优的模拟预编码矩阵FRF以最大化目标函数Y；考虑到FRF的特殊限制，这是一个非线性优化问题，直接优化自变量为矩阵的FRF将极为复杂；为了简化过程，对矩阵FRF做一个处理，将对矩阵的寻优转换为对矢量的寻优：考虑到FRF的式（5）矩阵形式，Nt×维的矩阵FRF可以转化成一个满足恒模限制的 1 ×Nt维矢量，定义这个 1 ×Nt维矢量为个体鱼的状态X，每一个状态X对应一个FRF。下面给出目标函数Y与个体鱼状态X的对应关系。

输入个体鱼的状态X。

步骤 1从候选解集合F中抽取 1 ×Nt维矢量作为个体鱼的状态X。

步骤 2把X的Nt个恒模元素按从左到右的顺序分为组，每组M个元素，第一组构成，第二组构成,…，第组构成。

步骤 3使步骤二的组矢量构成式（5）的块对角矩阵FRF，再恒模处理。

步骤4将步骤3的FRF代入式（8）计算得到的频谱效率作为目标函数Y。

输出 目标函数Y。

借鉴参考文献[12]的算法设计思想，提出本文基于AFS的混合预编码设计方法，具体步骤如下。

步骤1给定总迭代次数z、初始步长Step、拥挤因子δ、尝试次数Trynumber、鱼群数目num、视野范围Vision，初始化当前迭代次数m=1。

步骤 2初始化人工鱼群，随机从候选解集合F中选取num个 1 ×Nt维矢量（num条鱼）。

步骤 3计算每条人工鱼的目标函数值Y并将最大值Ymax记录在计分板。

步骤 4对人工鱼分别执行觅食、聚群、追尾算子。

对人工鱼执行觅食算子：人工鱼Xi利用式（10）在其视野范围Vision内随机选择一个状态为Xj的人工鱼，并分别计算它们的目标函数值；如果Yi＜Yj，则按式（11）所示，向Xj方向移动一步Step；若不满足前进条件，利用式（10）再次计算，重新选择状态Xj，并再次判断是否满足前进条件；重复尝试Trynumber次后，如果仍不满足前进条件，则按式（12）执行随机行为，其中 r an2(1,Nt)代表生成元素满足随机分布的1×Nt维矢量。

·对人工鱼执行聚群算子：人工鱼Xi探索周围的伙伴数目n+与中心位置Xc。如果满足Ycn+＞δYi，则表明伙伴附近食物浓度高、拥挤度低，此时人工鱼Xi向伙伴的中心位置Xc方向前进一步，形成新的状态Xnext，如式（13）所示；如不满足，回到步骤4。

针对风险较高的变电站，利用沙袋、玻璃胶、水泥等完成有效封堵和加固。11月14日，金沙江堰塞湖洪峰过境香格里拉市上江乡段，洪峰水位超变电站围墙1.6米，35千伏上江变电站正是因为提前预防，采取一系列封堵措施，提前填埋了三百多袋沙袋和水泥，严密封堵，避免了损失。

对人工鱼执行追尾算子：人工鱼Xi探索周围的目标函数最大的伙伴Xmax及人工鱼数目nmax，如果存在Ymaxnmax＞δYi，则表明伙伴Xmax的状态较优，具有较高的食物浓度并且周围不拥挤，此时按式（14）向Xmax方向前进一步并计算目标函数记录在计分板上；如果不存在，回到步骤4。若达到迭代次数仍然没有找到更优值，则取现有的最优值记录在计分板上。

步骤5m=m+1。

步骤6判断m＜z，若成立，回到步骤4。

步骤 7选取计分板中最大的状态值作为最后结果，算法结束。

对AFS算法应用变步长改进方法的具体步骤为将第m次迭代的步长Stepm变为初始步长乘迭代次数的反比例函数：

其中，kl为合适的反比例系数。通过在步骤5之后加入一个更新步长的步骤，这样处理可以使得迭代的步长随着迭代次数增加而变小，实现变步长的目的。改进后基于IAFS方法的混合预编码设计流程如图2所示，虚框部分为改进步骤。

图2 IAFS方法流程

4 仿真分析

本节利用MATLAB软件对OMP混合预编码方法、SIC方法、AFS方法、IAFS方法在理想CSI条件下进行计算机仿真，性能评价指标为频谱效率R与能量效率η。假设信道簇角度在[π6,5π6]上服从均匀分布，角度拓展设为10°。所有仿真结果均通过蒙特卡罗法对信道实现1 000次取平均得到的，信道与IAFS算法以及相关功率仿真参数见表1。

表1 仿真参数

图3给出Nt=1 28、Nr=16、=Ns=16时，不同大规模MIMO混合预编码方法所获得的频谱效率随着SNR的变化情况。由图3可知，随着SNR的增加，各混合预编码方法的频谱效率性能均有一定的提高。在低SNR（SNR＜-15 2B）时，IAFS方法与AFS方法频谱效率性能表现良好，与OMP方法十分接近。大约SNR为2 2B时，IAFS方法与SIC方法的曲线相交，因为IAFS方法数字端采用最大比传输准则设计，可以最大限度地增加用户的信号增益[15]，抗噪声能力强，所以在低SNR下有优势，但随着SNR增加其性能表现不如SIC方法。IAFS方法的频谱效率性能优于AFS方法，在SNR为10 2B与-10 2B时，大约分别有2.5bit(s·Hz)、1.1bit(s·Hz)的频谱效率增益，这是因为加入了变步长的改进，IAFS算法的性能更优越。

图3 =Ns条件下不同混合预编码方法的频谱效率

图4给出Nt=1 28、Nr=16、=Ns=1 6、SNR=02B时，IAFS与AFS方法所获得的频谱效率随着迭代次数z的变化情况。由图4可知，IAFS算法的收敛速度比AFS算法要快，大约在迭代次数为10次时，IAFS算法基本收敛，这是因为加入了变步长的改进，验证了IAFS方法的有效性。当迭代次数为50次时， IAFS方法接近收敛，两种混合预编码方法性能大致相等，体现了IAFS方法的优越性。

图4 IAFS/ AFS方法的Z与频谱效率的关系

图5给出Nt=1 28、Nr=6、Ns=6，SNR=02B时不同大规模MIMO混合预编码方法所获得的能量效率随着的变化情况，取=[ 8,16,32,64]。由图5可知：混合预编码方法的频谱效率性能随着在一定范围的增加会有所提升；对于 IAFS方法而言，从=8到=3 2，频谱效率提高了2.9bit(s·Hz)左右。大约当=1 6时，OMP方法的频谱效率性能不会再随着的增加而提升，而AFS方法与IAFS方法的频谱效率性能则不同，当从16增加到64时，ASF方法与IAFS方法的频谱效率性能大约分别提升了3.1bit(s·Hz)与3bit(s·Hz)。AFS与 IAFS方法在固定Ns=6时，可取不同的值，所以对于与Ns相等或者不等的大规模MIMO系统均适用。

图5 相同N不同条件下不同混合预编码方法的频谱效率s

图6给出Nt=2 56、SNR=-52B、=Ns=Nr时不同大规模 MIMO混合预编码方法所获得的能量效率随着的变化情况。由图6可知：随着增加，3种混合预编码方法对应的能量效率都呈现下降趋势，当由16变为32时，IAFS方法、SIC方法、OMP方法的能量效率分别大约下降了0.07bit(J·Hz)、0.26bit(J·Hz)、0.46bit(J·Hz)，OMP 方法能量效率下降的最为明显，这是因为该方法这个阶段由增加导致了相当多的能量损耗，而提升的频谱效率较为有限。基于部分连接结构的IAFS方法与SIC方法要比基于全连接结构的OMP方法对应的能量效率性能优秀，这是部分连接结构的优势所在，与理论分析相吻合。而同为部分连接结构的IAFS方法比SIC方法的能量效率性能表现更令人满意。

图6 不同条件下不同混合预编码方法的能量效率

5 结束语

针对部分连接结构毫米波大规模 MIMO系统，提出了一种基于 IAFS算法的混合预编码方法，通过将混合预编码设计转化为寻优问题，利用IAFS算法进行优化求解，从而完成混合预编码设计。与参考文献[8]相比，本文的方法对于输入数据流数与射频链路数不相等的毫米波大规模MIMO系统同样适用，且低SNR条件下，在频谱效率、能量效率性能方面有一定的优势，有望在异构通信等多种场景得到应用[16]。此外，IAFS算法中的变步长等相关参数能通过神经网络等工具予以优化，可作为下一步的研究工作