基于神经网络与马尔可夫组合模型的视频流行度预测算法

马学森，陈树友，许向东，储昭坤

（1.合肥工业大学计算机与信息学院，安徽 合肥 230601；2.中国电信股份有限公司研究院，广东 广州 510630）

1 引言

根据思科2020年的统计[1]，视频流量占据了整个网络流量的 80%。在传统网络架构中，用户的访问请求需要经过基站的接入、核心网的访问以及冗长的链路回传才能完成，频繁的用户请求容易造成核心网络的拥塞[2]。将热点视频在边缘侧进行缓存，一方面可以减少纵向流量，另一方面还能降低时延，提升用户体验[3]。

其中，各类视频门户网站的电视剧播放量又占据了绝大部分的视频流量，并且电视剧通常周期性地更新剧集。为了减少中心节点与边缘节点内容的反复迁移，将未来一个星期内流行度较高的视频放入缓存更有价值，因此对视频流行度进行准确的中长期预测成为急需解决的问题[4]。

传统的视频流行度预测模型大致分为两类：一类是以线性回归与自回归模型为代表的时间序列预测模型，参考文献[5-7]基于历史流行度构建回归预测模型，此类模型虽然训练简单，但非线性映射能力差，很难捕捉流行度的动态变化，并且无法保留时间序列上的信息依赖，随着时间步长的增加会逐渐失去对数据的学习能力，在中长期预测中表现不佳。另一类是基于特征提取与用户聚类的有监督学习方法来加强预测效果[8-9]，此类方法在一定程度上提高了模型的预测精度，但由于引入过多的外部变量，导致模型复杂度较高，极大地增加了模型的训练难度，不适用于实际应用场景。随着深度学习理论的不断发展，具有较强学习能力的循环神经网络（recurrent neural network，RNN）和长短期记忆（long short-term memory，LSTM）网络主要应用于模式识别、语音处理等方面[10]，近年国内外学者也将其应用在船舶航迹、小区的负荷指标等预测领域[11-12]，实验表明预测精度优于传统方法，但是在视频流行度预测领域的应用有待进一步研究。

基于以上分析，本文提出基于神经网络与马尔可夫组合模型的视频流行度预测算法，利用LSTM 结合双向 RNN构建双向长短期记忆（bi-2irectional long short-term memory，BiLSTM）网络模型，可以保留时间序列上两个方向的特征依赖；并且考虑马尔可夫具有根据系统当前状态对系统未来状态进行预测的性质[13]，利用BiLSTM 网络训练时产生的误差信息建立马尔可夫修正模型，在避免引入过多变量导致模型复杂度增加的情况下进一步提高了网络模型的预测精度。

2 基于神经网络与马尔可夫的预测模型

2.1 BiLSTM网络模型的构建

回归模型本质上是对数据的线性拟合，不容易捕捉非线性的波动趋势；传统的BP神经网络虽然可以有效地解决非线性映射问题，但在长时间序列训练过程中会出现梯度爆炸和梯度消失等问题。LSTM 通过引入控制门机制，可以在一定程度上避免此类问题，但LSTM的单向学习机制只能在一个方向上学习时间序列的数据特征。在视频流行度的预测中，某个时间点视频流行度的预测值，除了可由过去的数据进行推导计算，未来时刻的数据也对当前时刻流行度的计算有影响，因此本文在LSTM的基础之上融入双向RNN隐藏层构建BiLSTM网络模型。

BiLSTM网络模型如图1所示，BiLSTM通过神经元之间的双向隐藏层来保存两个输入方向的信息，可以有效学习流行度序列上两个方向的关系依赖，增强了模型的学习能力；同时通过多层神经网络的叠加结构实现了流行度序列深层次的特征挖掘，有效提高了模型的预测效果。

图1 BiLSTM网络模型

2.2 BiLSTM的马尔可夫修正

为了进一步提高模型的预测精度，如果通过继续引入特征变量的方式，新的变量会作为输入层的参数重新训练，过多的变量会导致模型训练困难。基于上述考虑，本文在不引入新的外部变量的情况下，通过对网络模型的预测误差建立马尔可夫修正模型来进一步提高模型的预测精度，如图2所示。

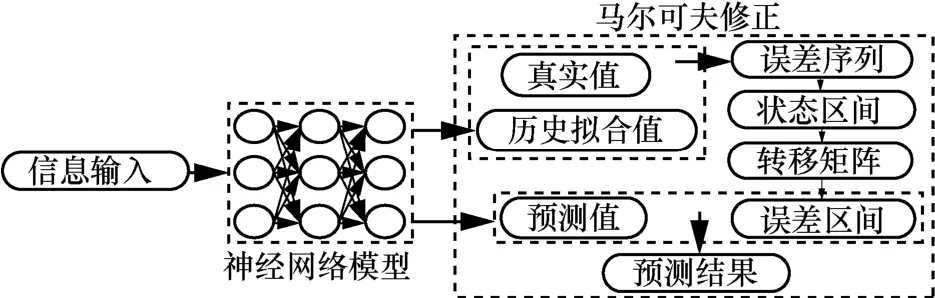
图2 马尔可夫修正模型

其中，Pt+1为t+1时刻error状态空间的概率分布，基于等距原则，进而求得误差修正值，如式（2）所示：

因此，本文视频流行度的预测模型可以定义为式（3），其中pre2icti为网络模型的预测值，mi22lei为求得的修正值，最终视频流行度的求解可以转化为Finali的求解：

3 Mar-BiLSTM算法设计与求解

3.1 视频流行度的预测问题描述

电视剧周期性地更新剧集，其中内容热度可以体现当前剧集的受欢迎程度，用序列Popularity={popularity1,popularity2,… ,popularityn}描述电视剧当前时刻的流行度。其中内容热度Popularity由平台综合播放量以及互动因子等指标计算，更加能够反映视频的流行度。研究指出，电视剧的微博搜索指数和百度搜索指数与电视剧流行度具有很强的线性关系[14]，因此分别构造微博指数序列 In 2ex1={in2ex11,in2ex12,…,in2ex1n}和百度搜索指数序列 I n2ex2={in2ex21, in2ex22,…,in2ex2n}；另外在新剧集更新当天的电视剧播放量会比平常有一个明显的增加，因此利用One-hot编码构造序列 F lag={+ l ag1, +lag2,… , + lagn}标记该变化，其中+lag1代表星期一，+lag7代表星期日；最后利用预测模型φ预测下一个时间单位的电视剧流行度，如式（4）所示。

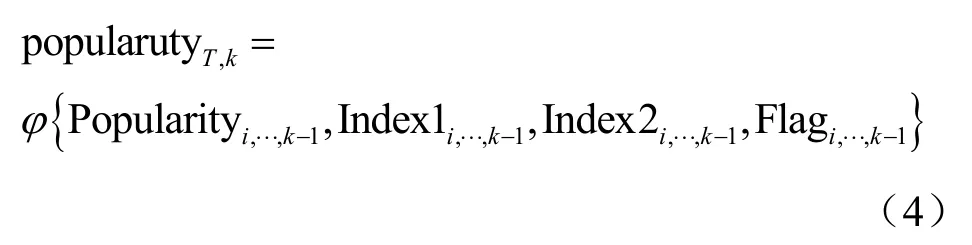
问题定义：在线电视剧T，已经上线i天，流行度记为Popularity，特征序列为Feature，预测目标为未来几天流行度的记录{popularityi+1,popularityi+2,… ,popularityi+n}。

3.2 Mar-BiLSTM流行度预测算法

基于第2.2节构建的马尔可夫修正的BiLSTM网络模型，本文设计了Mar-BiLSTM算法来求解视频流行度预测问题，算法框架如图3所示。

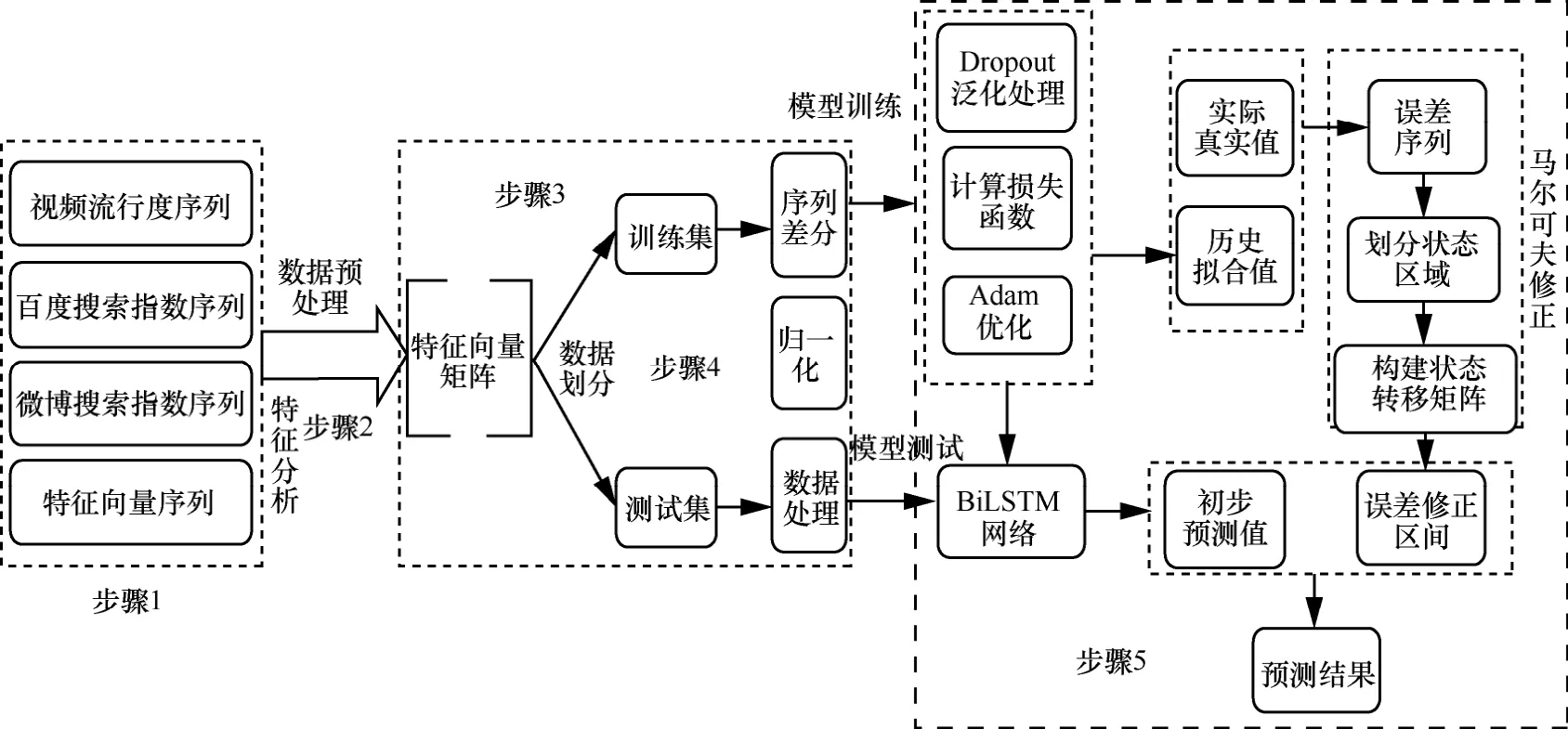
图3 Mar-BiLSTM算法框架

Mar-BiLSTM算法大致可以分为5个步骤，算法的详细流程如下。

步骤1基于Scrapy技术对电视剧的流行度进行特征分析，得到In2ex1、 I n 2ex2、 F lag 等特征序列。

步骤 2获取电视剧从上线开始后 3个星期的内容热度值popularityi，微博搜索指数值in2ex1i，百度搜索指数in2ex2i；+lagi表示当天是否为剧集更新日，当+lagi=1时表示当天有剧集更新，+lagi=0 时表示当天没有剧集更新；进而根据特征向量序列构建特征向量矩阵。

步骤 3利用特征向量Feature进行模型训练，取序列Popularity前两个星期的数据作为模型的训练数据，最后一个星期的数据用于模型的检验；同时将序列处理为适合监督学习的数据。

步骤 4对序列进行差分处理，以此减小数据波动对模型训练的影响；同时采用min-max策略对原始数据进行归一化处理来消除量纲的差异，其转换如式（5）所示：

步骤 5采用自适应估计方法计算每个参数的学习率；同时为避免过拟合现象采用 2ropout机制来提高模型的泛化能力；最后利用网络模型的预测误差建立马尔可夫修正模型，根据式（3）得到修正后的流行度预测值Finali。

Mar-BiLSTM算法实现的伪代码如算法1所示。

算法1Mar-BiLSTM算法

输入训练集 Train_set，测试集 Test_set，属性（特征序列）

输出视频流行度预测值

步骤1进行特征分析，得到特征序列：

Popularity={popularity1,popularity2,…,popularityk},

k=1,2,…,21

In2ex1={in2ex11,in2ex12,…,in2ex1n},n=1,2,…,14

In2ex2={in2ex21,in2ex22,…,in2ex2m},1,2,…,14

Flag={+lag1, +lag2,…,+lags},s=1,2,… ，14

步骤2将各个时间序列进行整合得到输入时间序列：

concatSequence (i,i+ 1,…,t)

步骤3将时间序列数据转化为有监督数据：

I+I＞n_in an2I＜ 0

input sequence (t -n, …,t-1)

Else i+I＞ 0 an2I＜n_out

+orecast sequence (t,t+ 1, …,t+n)

步骤4max-min特征变换：

Return (Train_set)

Return (Test_set)

步骤5Train_set Train BiLSTM-Markov

Test_set Test BiLSTM-Markov

Return（均方根误差、平均绝对误差）

Return（流行度预测值）

en2

Mar-BiLSTM算法时间复杂度可分为5个部分。

步骤1时间复杂度可以记为O(|m|)；

步骤2序列整合的时间复杂度为O(|m|)；

步骤 3序列转化为有监督数据的时间复杂度为O(|n||m|)；

步骤 4max-min特征变换的时间复杂度为O(|n||m|)；

步骤 5计算均方根误差及平均绝对误差的时间复杂度为O(|n||m||i|)；因此，Mar-BiLSTM算法的时间复杂度为O(|n||m|)。

4 实验设计与分析

4.1 实验环境

实验环境为联想 Thinkpa2 E440笔记本计算机，CPU为Intel® CoreTM i5-4210 CPU @ 2.60 GHz，内存为8 GB，操作系统为Bin2ows10教育版，使用基于Python3.5语言的PyCharm社区版集成开发工具构建神经网络模型，利用MATLAB R2018b开发工具进行对比试验设计。

4.2 评价指标

实验采用预测模型常用的均方根误差（root mean square2 error，RMSE）及平均绝对误差（mean absolute error，MAE）作为预测性能的评价标准[15]。RMSE可以评价数据的变化情况，RMSE值越小，表示模型有更好的预测精确度，MAE可以更好地反映预测值与真实值偏离程度的实际情况，如式（6）、式（7）所示。

4.3 网络模型参数选择

隐藏层的层数以及神经单元个数的选择对网络模型的性能影响很大，因此需要选择训练误差最小的网络参数。不同W值下的RMSE值如图4所示，在隐藏层数W=2、隐藏层单元个数L=6时的RMSE值最小，过多的隐藏层或者单元数都会使得网络过于复杂而丧失网络优势。因此，选择W=2、L=6作为网络模型的训练参数。

图4 不同W值下的RMSE值

4.4 实验设计及结果分析

实验爬取电视剧《爱情公寓5》自2020年1月12日上线到同年2月1日的全网数据（其中包括播放量、评论数、点赞数、收藏数、百度搜索指数与微博搜索指数等），使用前两个星期的数据训练模型、后一个星期的数据用来验证本文算法的优越性：首先选取回归模型中常用于时间序列预测的灰色预测（grey mo2el，GM）与指数平滑（exponential smoothing，ES）验证算法的有效性，进而选取神经网络中常用于时间序列预测的传统BP神经网络和 LSTM 神经网络验证算法的优越性；最后通过爬取2021年1月至2021年3月期间的10部首播电视剧的数据对其排名进行预测，以此验证算法的普适性。

4.4.1 LSTM与回归模型对比

本节设计LSTM与GM、ES之间的对比实验，以此来验证 LSTM 的预测精度优于传统回归模型。

GM、ES及LSTM模型的预测值对比如图5所示，由于流行度数据不符合幂指数规律，因此基于指数规律建模的GM没有很好地预测数据的波动规律；ES利用序列差分机制，可以预测很小的波动，但并不吻合真实数据的波动规律；LSTM基于 RNN与门控单元机制可以学习长时间序列上的信息依赖，对未来数据的波动给出了大致的

图5 GM、ES及LSTM模型的预测值对比

预测，验证了 LSTM 的预测效果优于传统回归模型。

4.4.2 BiLSTM与BP、LSTM模型对比

本节设计了LSTM网络与BP神经网络之间的对比试验，就其预测精度及其收敛性进行分析；在此基础之上，引入BiLSTM进行对比实验，以此验证BiLSTM的优越性，为Mar-DBiLSTM组合预测理论模型提供实验数据支撑。

BP、LSTM 模型训练误差如图6所示。BiLSTM、BP、及 LSTM 模型预测值对比如图7所示。从图6可以看出，LSTM较BP神经网络的收敛速度要快，在迭代次数为200次左右时，网络已经趋于收敛，此时BP神经网络的训练误差还处于较高水平；同时从图7可以看出，BP神经网络虽然能够预测数据大致的波动趋势，但 LSTM的预测曲线更加贴合于真实值，因此LSTM不仅学习性能强于传统的神经网络，而且其预测效果也优于普通的BP神经网络；基于LSTM改进的BiLSTM 可以学习时间序列上两个时间方向的信息依赖，因而能够更好地对数据的波动趋势进行学习，从图7也可以看出，BiLSTM较LSTM、BP均具有更高的预测精度，验证了本文BiLSTM模型预测效果的优越性。

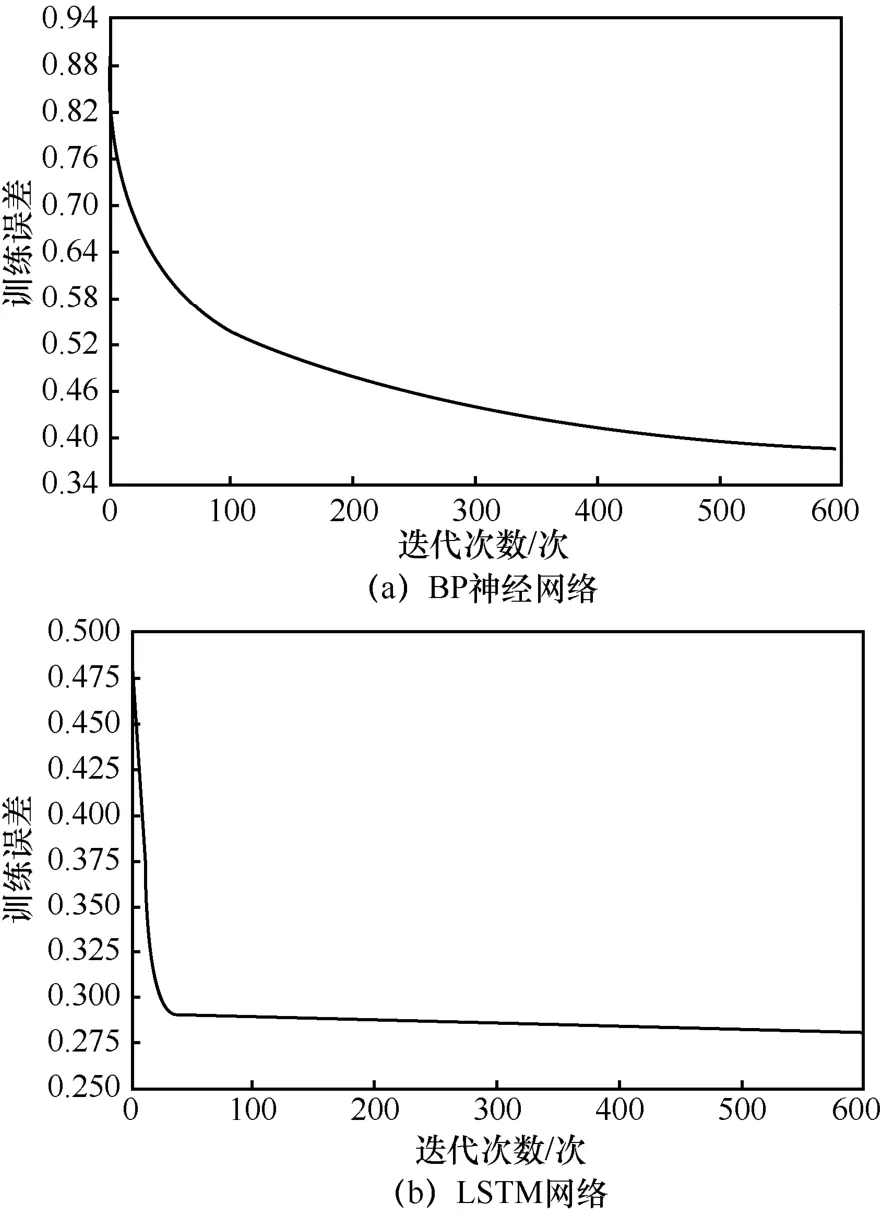
图6 BP、LSTM模型训练误差

图7 BiLSTM、BP及LSTM模型预测值对比

4.4.3 Mar-BiLSTM与BiLSTM模型对比

在前两轮实验的基础之上，为了验证Mar-BiLSTM 算法的有效性，设计该对比实验。通过第2.2节的描述，对BiLSTM的预测误差构建马尔可夫修正模型，最终可以求得未来几天预测误差可能的状态区间，见表1。

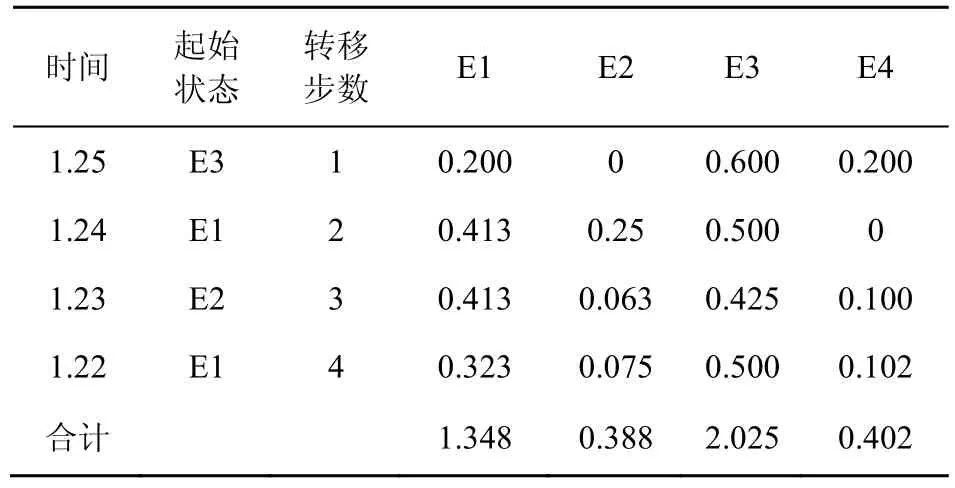
表1 模型预测误差状态区间

由表1可知，26号最有可能的误差状态区间为 E3，由式（2）计算得到误差修正值为 22，BiLSTM模型的预测值为9 096，根据式（3）得到修正后的预测值为9 091。在对27号误差状态进行预测时，将26号误差预测值作为已知值，并将最原始的信息剔除，按照上述方法重复，可以计算出接下来6天的误差修正值。

由图8可知，经马尔可夫修正过的BiLSTM预测值要更加贴近真实值，预测效果更好，证明了本文算法的优越性。

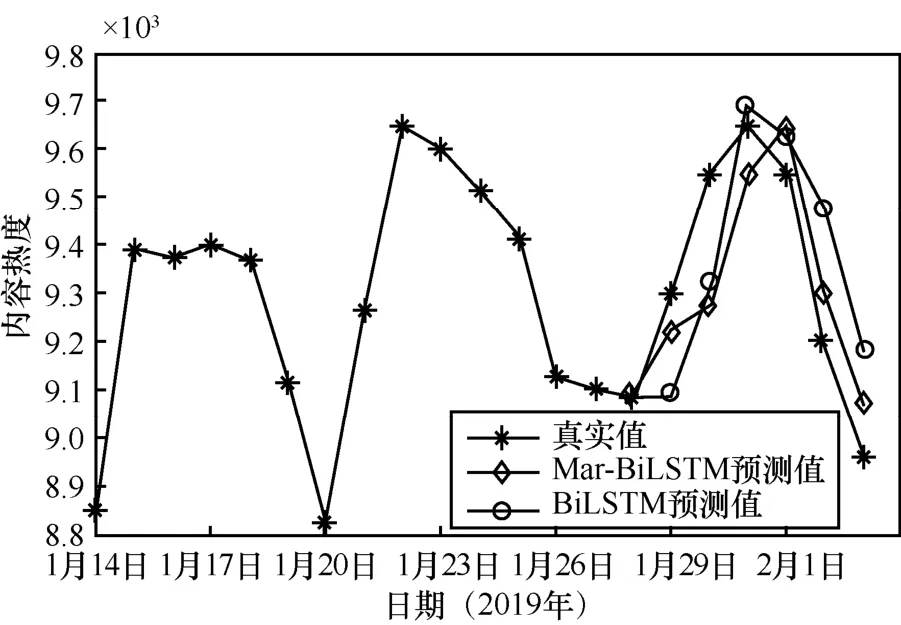
图8 Mar-BiLSTM、BiLSTM模型预测值对比

综上，根据第4.2节提出的性能指标，给出对比预测模型的性能分析，见表2。

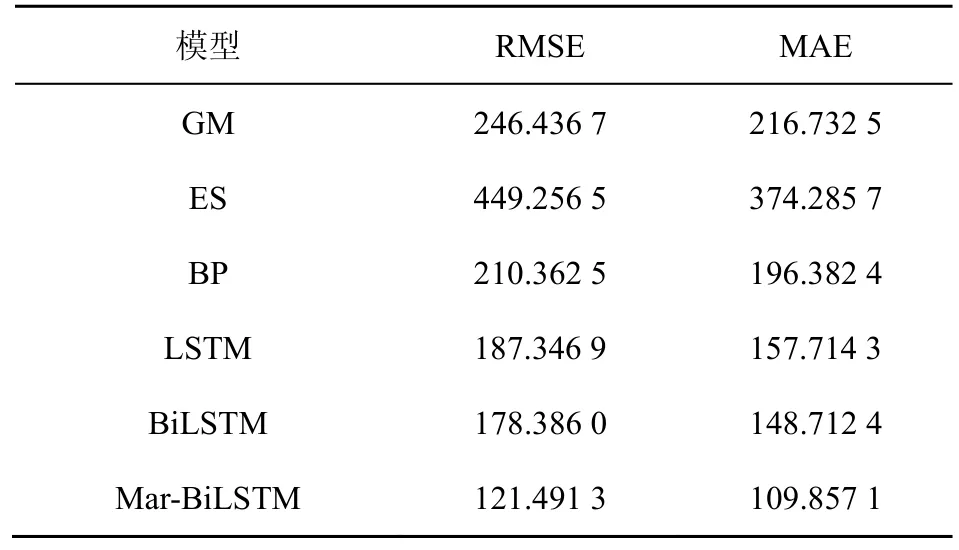
表2 性能对比

4.4.4 电视剧排名预测

为了进一步验证算法的普适性，从全网爬取2021年1月至3月期间首播的10部不同种类的电视剧数据，并对其排名进行预测。由于电视剧并非在同一时间上线，其上线时间越长，累积播放量会越高；并且由于剧集数的不同，累计播放量也会有相应的影响。因此，为了更加准确地体现电视剧的真实排名，选择均集播放量和均天播放量的加权值作为衡量电视剧真实排名的依据，排名预测结果见表3。

从表3可以看出，排名靠前的《斗罗大陆》《锦心似玉》《爱的理想生活》等热播电视剧得到了准确的预测，排名靠后的《你好，安怡》和《这个世界不看脸》等冷门电视剧也有较好的预测。因此，本文算法对不同类型电视剧的流行度均给出了不错的预测效果，证明了算法的普适性较高。

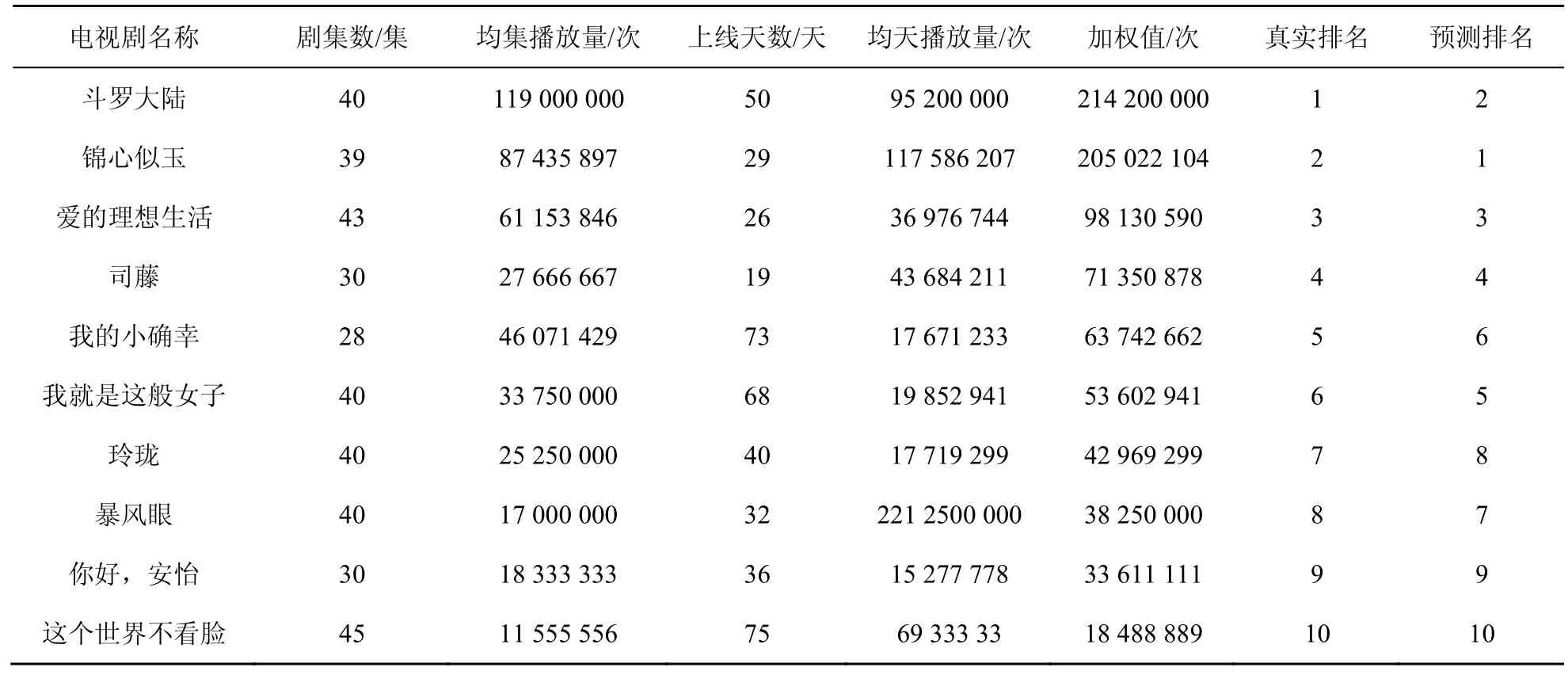
表3 电视剧排名预测结果

5 结束语

本文针对传统视频流行度预测算法非线性映射能力差，在中长期预测中存在精度低、自适应性弱等缺点，提出基于神经网络与马尔可夫组合模型的视频流行度预测算法。该算法在预测过程中兼具时间相关性和非线性的特征，充分保留了时间序列上前向、后向两个方向的长期依赖信息；并利用BiLSTM网络训练时产生的预测误差建立马尔可夫修正模型，在避免引入过多变量导致模型复杂度增加的情况下进一步提高了模型的预测精度。下一步工作拟将 Mar-BiLSTM 算法引入边缘侧的缓存调度策略中，尝试建立根据视频流行度预测的缓存替换策略，提高用户的服务体验质量。