底水油藏特高含水期认识剩余油潜力的新方法

孙恩慧，张 东，郭敬民，刘博伟，张小龙

(中海石油(中国)有限公司 天津分公司，天津 300452)

底水油藏进入特高含水期时，波及体积趋于定值，提高采收率主要方式为提高驱油效率，而过水倍数是影响波及区域内最终驱油效率的决定性因素。室内实验表明[1-3]，在特高含水期增加岩心的过水倍数可进一步提高驱油效率。目前关于注水驱油田的驱油效率研究较多[4-6]，但是，针对天然底水油藏的驱油效率理论研究较少。本文从过水倍数和驱油效率的定义出发，利用达西定律和物质平衡理论，推导出底水油藏不同过水倍数与驱油效率的关系式。该方法可定量计算老井特高含水阶段的剩余潜力，有效指导生产井后续的措施挖潜方向。

1 底水油藏过水倍数与驱油效率理论关系的推导

在特高含水阶段，传统的Kro/Krw与Sw之间的直线关系式，不再适用于特高含水期。文献[7]中提出特高含水阶段下Kro/Krw与Sw关系新的表达式，很好地拟合特高含水期的非线性规律，具有广泛的适应性。

(1)

式中：Kro为油相相对渗透率，无因次；Krw为水相相对渗透率，无因次；Sw为含水饱和度，%；a、b、c为拟合系数(函数拟合时，相关系数最大值对应的拟合系数)，可用最小二乘法求解。

单井在某一时刻的产油量可以表示为：

(2)

式中：Qo为某一时刻的产油量，m3/d；t为生产时间，d；Np为累产油，104m3；Vh为单井水脊体积，104m3；Swi为束缚水饱和度，%。

根据达西定律，考虑在一维条件下，忽略毛细管力和重力的作用，地面水油比可表示为：

(3)

式中：Qw为某一时刻的产水量，m3/d；ρw为水的密度，g/cm3；ρo为原油的密度，g/cm3；μo为地层原油黏度，mPa·s；μw为水黏度，mPa·s；Bo为地层原油的体积系数，无因次；Bw为水的体积系数，无因次。

某时刻水平井的累产水量表示为：

(4)

式中：Wp累产水量，104m3。

将(1)、(2)、(3)式代入(4)式，可得：

(5)

根据油藏物质平衡理论，可得：

We-Wp=(Sw-Swi)Ahφρw/Bw

(6)

式中：We为水侵量，104m3；A为含油面积，km2；h为油层厚度，m；φ为孔隙度，%。

根据定义，过水倍数可表示为：

(7)

式中：PV为过水倍数，无因次。

在实验室中，一般可以用下式计算岩心的驱油效率：

(8)

式中：ED为驱油效率，%。

将(5)、(6)、(7)代入(8)式中，驱油效率则可表示为：

(9)

式(9)为底水油藏特高含水期下的不同过水倍数PV与驱油效率ED的关系式。

2 底水油藏过水倍数与驱油效率关系的求解方法

从(9)式中看出，如果想求解不同过水倍数与驱油效率关系，需要知道不同过水倍数下的a、b、c的值，含水饱和度Sw的值和Vh的值。

2.1 a、b、c值的求解

相渗曲线(见图1)一般采用指数表达形式进行表述[9]:

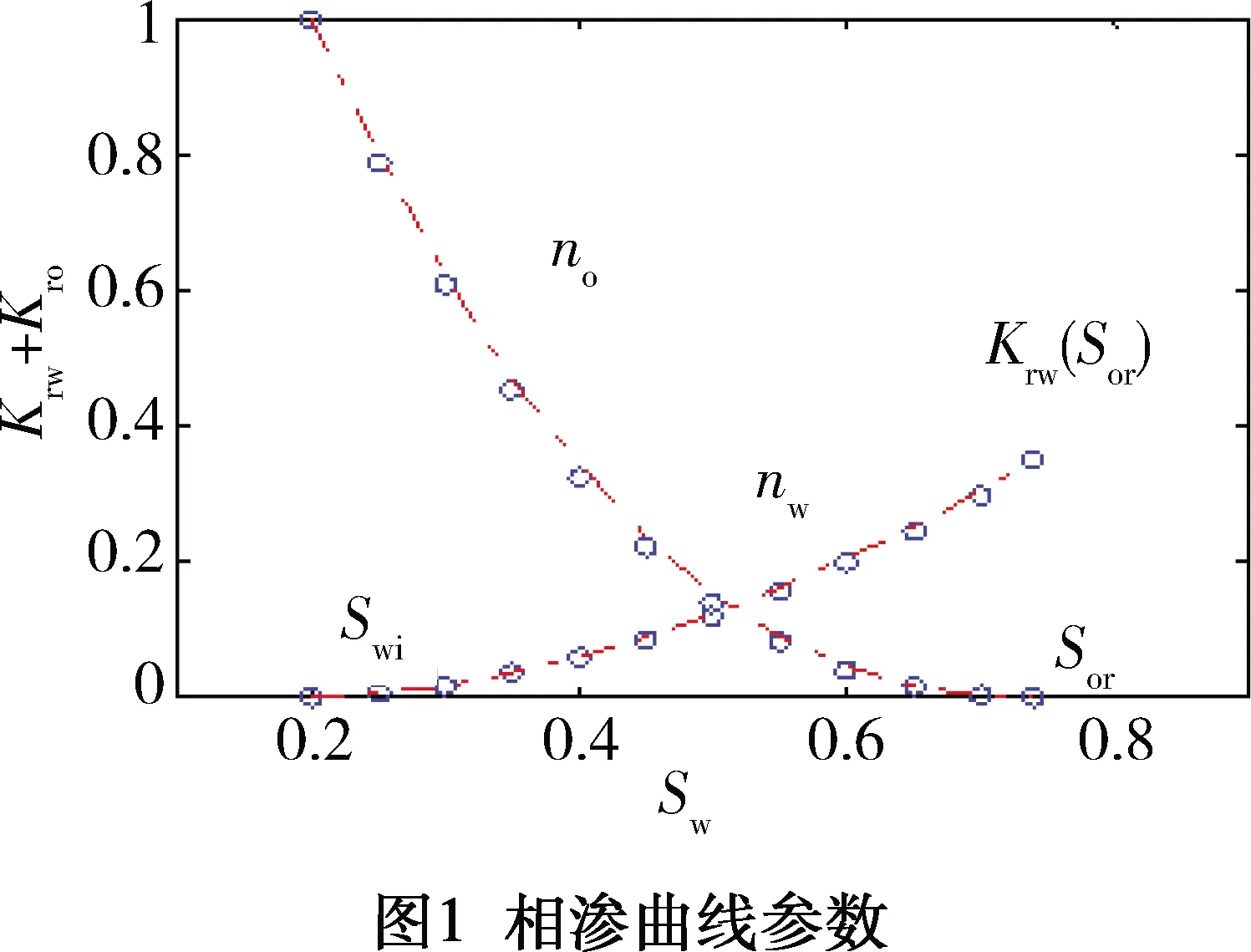
(10)

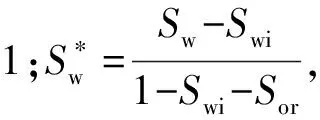
式(10)中，Swi可利用测井等方法测取，Sor、Cw和Co可利用拟合油藏生产动态资料确定。

遗传算法是一种通过模拟自然进化过程搜索最优解的方法。如图2所示，首先通过公式(10)，利用已知相渗关系式的特征参数作为初始值，然后产生不同特征参数条件下的相渗曲线作为初始种群，计算不同参数时对应的含水率与采出程度曲线，将得到的曲线与实际曲线作对比，如果不满足终止条件，循环迭代直至满足终止条件。

通过遗传算法，得到不同过水倍数下的相渗曲线的Sor、Cw和Co参数，利用非线性回归方法得到不同过水倍数下的a、b、c的值。

2.2 含水饱和度Sw值的求解

在一维条件下，忽略毛细管力和重力的作用，根据达西定律可以得到水相分流量曲线表达式：

(11)

式中：fw为含水率，%。

把式(1)带入式(11)中，得到：

(12)

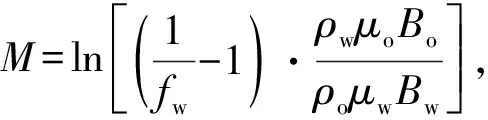
在式(12)中，a、b、c的值通过上述方法已经获得，就得到不同含水率fw与含水饱和度Sw的关系，知道了水平井的含水率fw，便可求出含水饱和度Sw。

2.3 水脊体积Vh值的求解

图3为底水油藏水平井水脊剖面示意图。

在描述底水油藏水平井水脊动态规律研究方面，目前常用式(13)拟合水脊形态：

f(r)=a1+a2e-a3r2

(13)

式中：a1、a2、a3为常数，与油层有效厚度、避水高度、地层原油黏度、储层各向异性、生产情况等因素有关，可以利用数值模拟的方法进行多因素回归分析，以确定水脊形态的描述公式。

考虑井距、渗透率比值、产液速度、避水高度、油水黏度比等因素，通过运用正交试验设计，得到水平表(见表1)。

表1 各参数水平表

在选定因素水平的试验数值之后，依照L27(38)正交表排出了正交试验设计的27种方案。通过底水油藏机理模型利用数模方法，预测了不同参数条件下的最终水脊体积。以某砂体一口水平生产井为例，通过非线性回归确定出式(13)中各参数表达式为：

(14)

水平井的水脊体积：

(15)

式中：W为井控长度，m，L为水平井长度，m。

已知水平井的基本参数，带入式(14)中，可以得到a1、a2、a3的值，把它们带入式(15)中，就可以得到不同过水倍数下的水脊体积Vh的值。

3 实际应用

C17H为某一强底水油藏投产的一口水平井，基本参数如下：渗透率3 000 mD，地下原油黏度350 mPa·s，水平井长度250 m，油层厚度15 m，避水高度10 m，井距200 m，目前产液量1 000 m3/d，含水率95%，Kv/Kh=0.1。

利用遗传算法，通过拟合实际动态(见图4)，得到不同过水倍数下的相渗曲线(见图5)，利用非线性回归方法得到:a=10，b=2.3，c=3.6。

将a、b、c的值带入式(15)中，得到

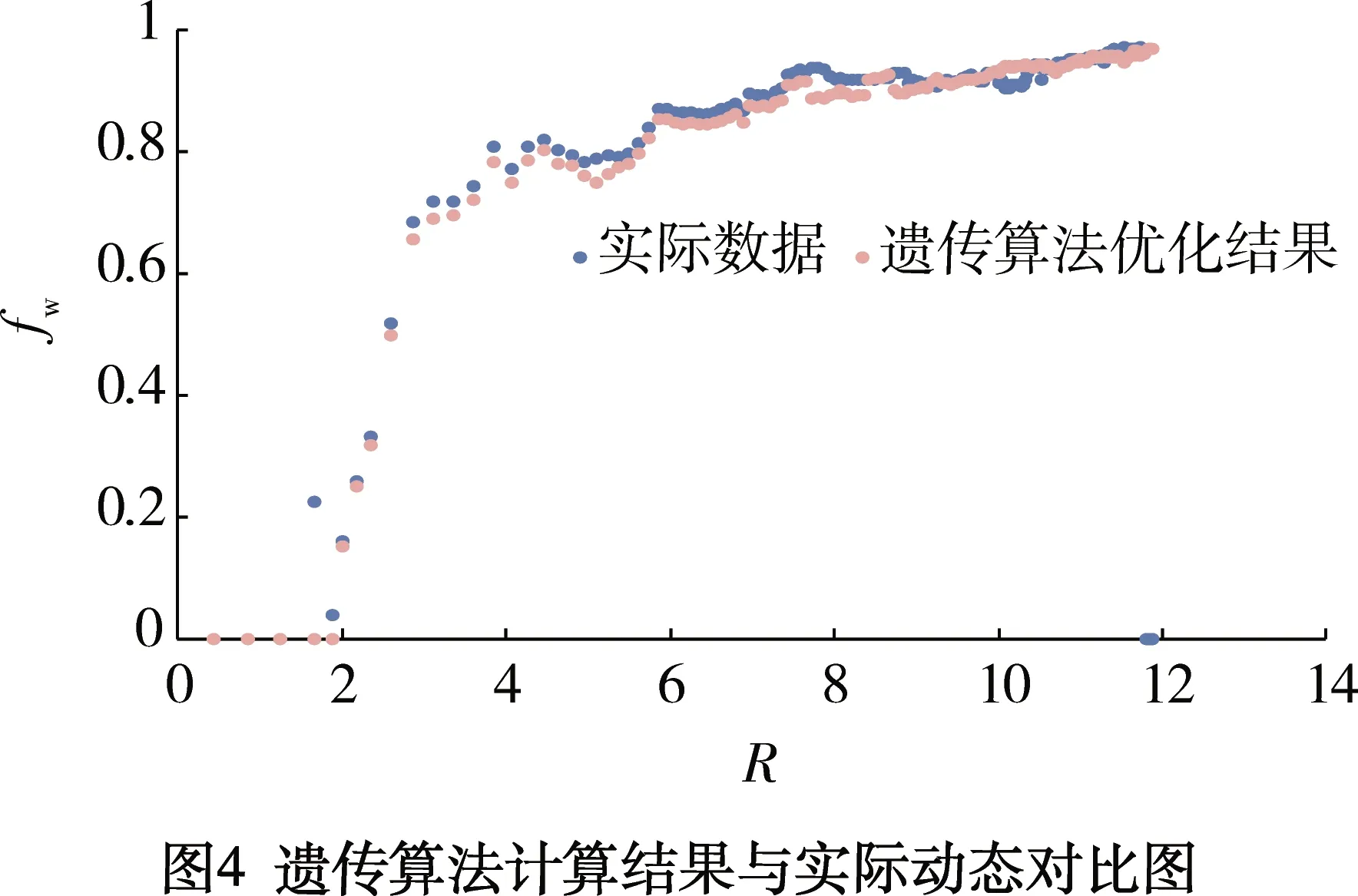
把不同过水倍数下的a、b、c的值，不同含水率fw与含水饱和度Sw的关系式以及不同含水率下的水脊体积Vh的值分别带入公式(9)中，得到底水油藏特高含水期下的不同过水倍数PV与驱油效率ED的关系(见图7), 预测C17H井的剩余可采储量计算结果见表2。

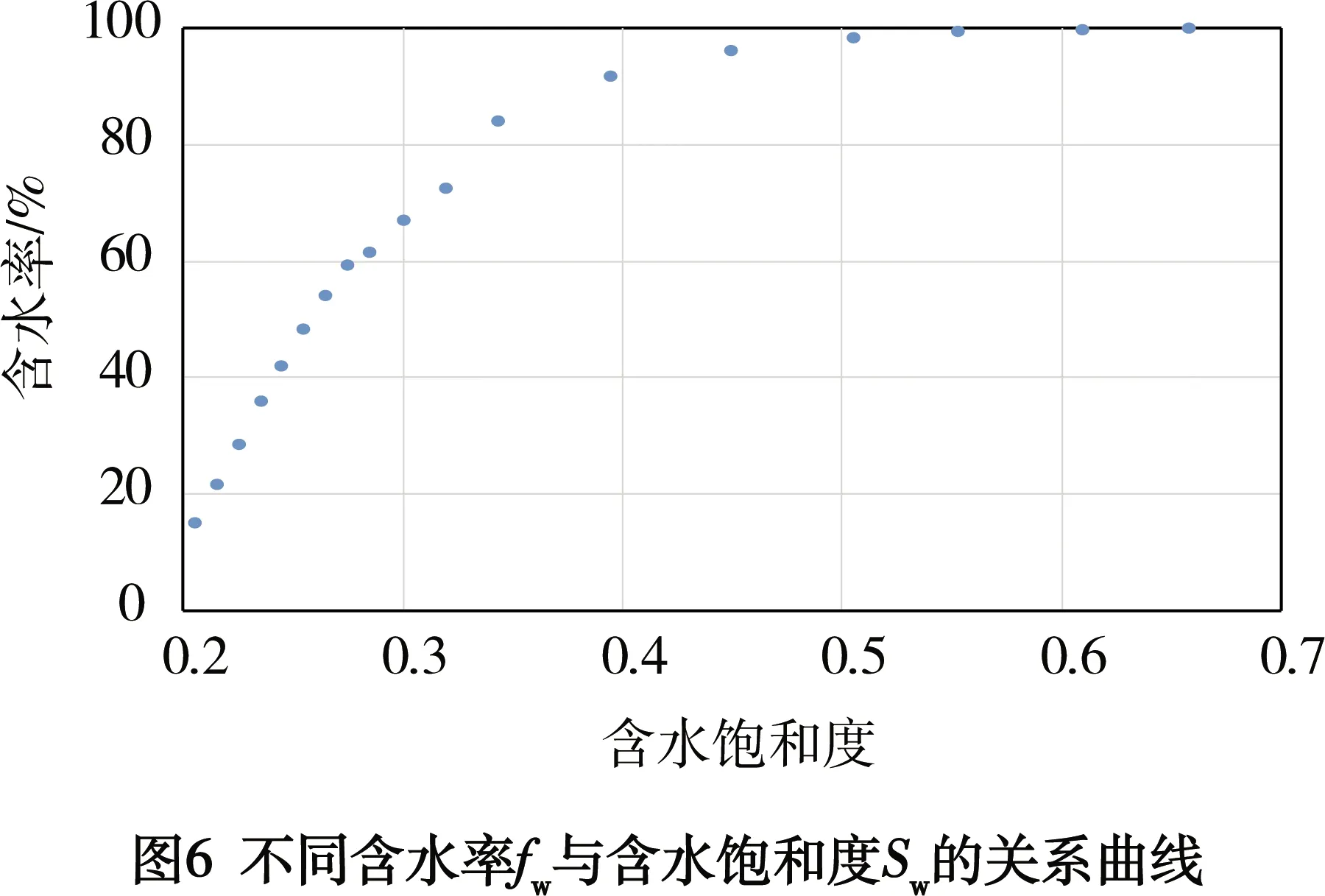
表2 预测C17H井的剩余可采储量计算结果

由表2中可以预测,C17H井含水率为98%时，剩余可采储量为6.6×104m3，剩余潜力较大。2020年5月初，C17H井提液日产液由700 m3增加到1 100 m3，日产油由44 m3增加到56 m3，因此，通过该方法可定量计算底水油藏特高含水期老井的剩余潜力，为单井后期的剩余油挖潜方案提供理论依据。

4 结论

1)推导出了底水油藏特高含水期下的不同过水倍数PV与驱油效率ED的关系式。

2)通过实例表明，运用本文方法可以预测油藏进入特高含水期时的剩余油潜力分布，为油田特高含水期的剩余油挖潜提供指导。