基于机器学习的ET0跨站适应性研究

董建华，刘小刚，吴立峰，黄国敏，杨启良

(1 昆明理工大学 农业与食品学院，云南 昆明 650500；2 南昌工程学院 水利与生态工程学院，江西 南昌 330099)

参考作物蒸散量(reference crop evapotranspiration,ET0)是作物灌溉等领域的重要参数之一，准确计算ET0是气候变化分析和区域水资源管理的关键环节[1-2]。ET0是由多种气象因子组成的函数，而气象因子通常与地理位置和气候类型有关[3]。联合国粮农组织(FAO)将Penman-Monteith方程确定为计算ET0的标准方程(FAO-56 PM)，常被用于衡量其他方程的准确性[4]。但FAO-56 PM对气象数据的完整性要求较高，导致FAO-56 PM在气象资料缺失地区的应用受到一定限制。因此，在有限的气象资料下，开发更高效的ET0估算方法具有重要的实际意义。

目前已有一些在有限气象资料下估算ET0的经验模型[5-7]，但因受地域环境影响较大而难以推广使用[8]。近年来，机器学习模型因具有更高的估算精度等而倍受关注，现已用于有限气象数据下ET0的估算[9]。吴立峰等[8]评估了多元自适应回归样条(multivariate adaptive regression splines,MARS)模型和支持向量机(support vector machine,SVM)模型在江西鄱阳湖地区有限气象数据下估算ET0的潜力,表明温度参数影响力最大。但此类研究的前提是研究区存在有限气象数据(如温度和辐射数据等)，而实际研究中存在部分站点完全缺失或仅有不完整气象数据，气象数据序列的缺失使ET0的估算受到明显影响。

由于部分地区缺失气温等气象数据会使ET0的估算受到影响，故学者们尝试借助研究区周边站点(邻站)气象信息通过插值估算目标站点ET0。目前，关于借助邻站气象信息的有关研究总体可分为4类：1)当本地历史气象信息完全缺乏时，可借助邻站气象信息和邻站建立的ET0模型来估算本地ET0。如张学梅等[10]在内陆干旱地区直接采用邻站气象数据结合人工神经网络(artificial neural network, ANN)模型，成功估算了目标站点的ET0月值。Karimi等[11]在韩国潮湿地区的7个辅助站和8个目标站中，直接使用辅助站点气象数据依次估算目标站点ET0值，构成56种建模情景，推荐使用基因表达式编程(gene expression programming, GEP)作为通用模型。Sanikhani等[12]也指出，机器学习模型的估算精度优于经验模型，且本地缺失数据时跨站输入具有可行性。2)本地有历史观测信息，但由于迁站等原因缺乏现阶段气象信息时，可以使用本站历史信息建立的ET0模型和邻站气温等数据来估算本地ET0。Shiri[13]评估了一种混合小波随机森林算法在伊朗南部5个气象站估算ET0的潜力，其先用本站历史数据对模型进行训练，再用邻站数据对模型进行测试，表明混合模型性能优于经验模型。Shiri等[14]还在伊朗西北部地区使用了本地历史数据所训练的GEP模型，表明结合邻站数据所得模型的性能优于完全邻站数据输入模式下模型的性能。3)当本地部分数据缺失时，可建立本地与邻站融合的新数据集来估算本地ET0。Feng等[15]将两站点间的温度和辐射数据进行重组，输入随机森林(random forests,RF)模型和广义回归神经网络(generalized regression neural networks,GRNN)模型中，并使用K折交叉验证法估算ET0值，均能准确估算中国四川省跨站模式下的ET0。Kisi[16]在土耳其不同区域站点中，使用邻站气象数据对缺乏部分本地数据的目标站点的ET0进行校正及插值估算，推荐使用M5模型树(M5 Tree)作为估算模型。Wu等[17]研究了当鄱阳湖地区的本地站点只有辐射数据时，可将其与对应邻站温度数据进行结合组成新数据集来建模，在该模式下MARS和SVM模型估算性能更佳。4)使用周边ET0和地理信息直接估算本地ET0。Shiri等[14]直接使用1个邻站ET0数据估算目标站点ET0，所得估算精度略逊于含本地数据输入模式下的估算性能。还有学者指出，在缺乏本地气象数据时，可以直接使用对应邻站的地理数据(如经纬度和海拔高度等)作为输入直接估算本地ET0值[18]。

从以上研究可以看出，前人多通过借助邻站气温、辐射、相对湿度和风速等基础气象数据来实现数据资料不足地区的ET0估算。在鄱阳湖地区，已有学者利用邻站的气温和辐射数据来估算目标站点的ET0值[8,17]，表明该地区跨站输入具有可行性。然而，由于鄱阳湖地区辐射、相对湿度和风速空间变异较大，仅借助气温信息难以保证ET0的估算精度。为此，本研究尝试将邻站ET0数据和本地部分数据相融合，用2种流行的机器学习方法(支持向量机(SVM)模型和极限梯度提升法(extreme gradient boosting,XGBoost)模型)进行ET0估算，并评估其适用性，以期为江西鄱阳湖地区灌溉制度的确定和水分的高效利用提供依据。

1 材料与方法

1.1 研究区域概况

江西省位于长江中下游，面积约16.69万km2。赣北为鄱阳湖平原，其他三面环山。气候属于中亚热带温暖湿润季风气候，由于降雨量较多，常导致涝灾。多年年均气温为16.3～19.5 ℃，且由南向北、自东向西逐渐递减[19]。当地最主要农作物为水稻。

1.2 数据来源

所选站点资料及其在江西省的地理位置如图1和表1所示。本研究选取江西省吉安和鄱阳2个站1966-2015年逐月气象资料，包括最高温度(Tmax)、最低温度(Tmin)、相对湿度(RH)、地表总辐射量(Rs)、地外总辐射量(Ra)、2 m高风速(U2)及对应邻站ET0、Tmax、Tmin、Rs(分别对应用ET0-ex、Tmax-ex、Tmin-ex和Rs-ex表示)数据。其中吉安站点对应邻站为宜春、夏坪、赣县和广昌站点，鄱阳站点对应邻站为景德镇、庐山、南昌和贵溪站点。此外，相对于经纬度信息，加入站点海拔信息对模型性能无明显提升，所以将邻站的经纬度信息也作为输入因子与气象因子共同输入到模型中。

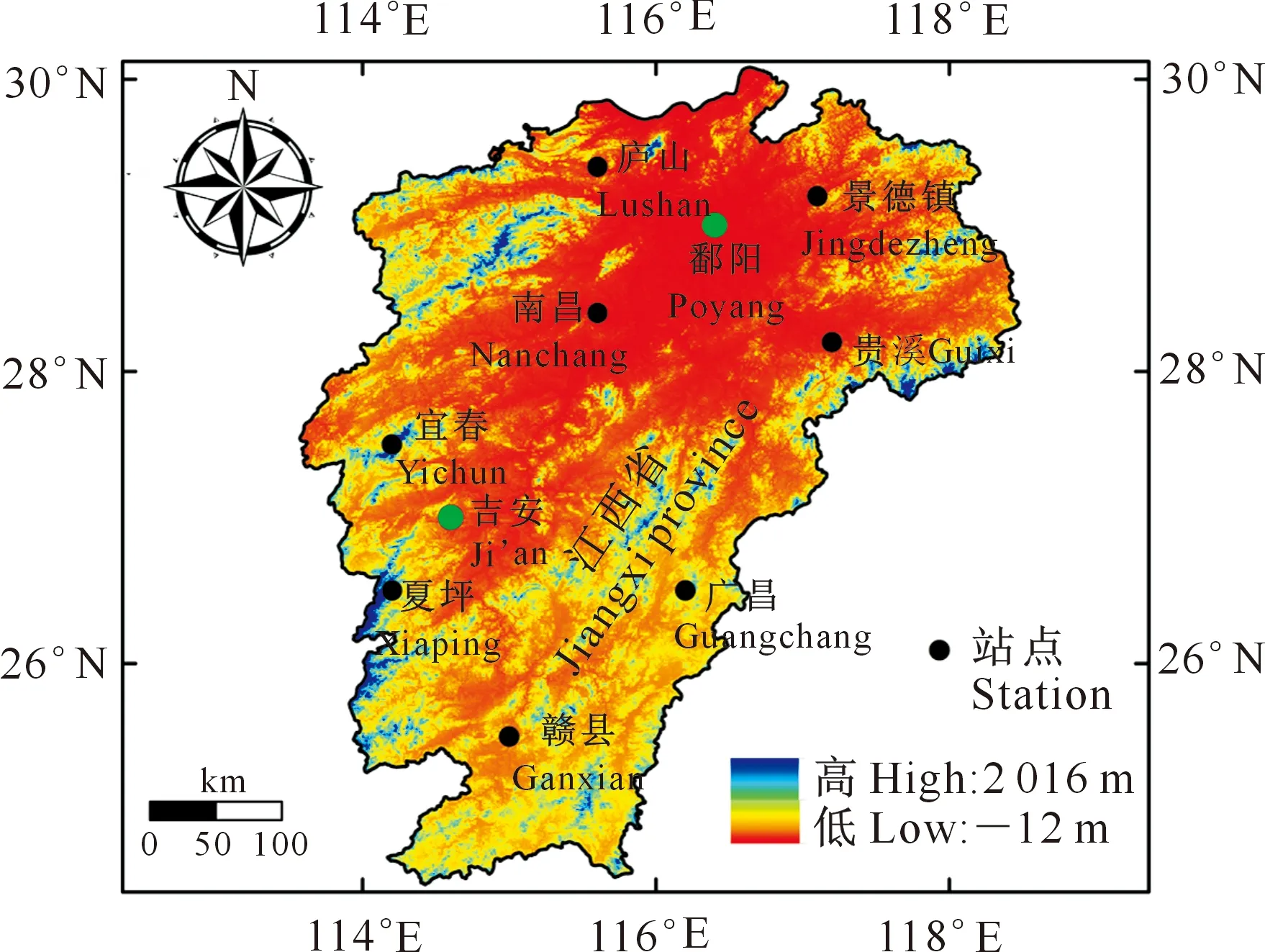
图1 研究区域位置及所涉及气象站点的空间分布Fig.1 Location of the study area and spatial distribution of related meteorological stations

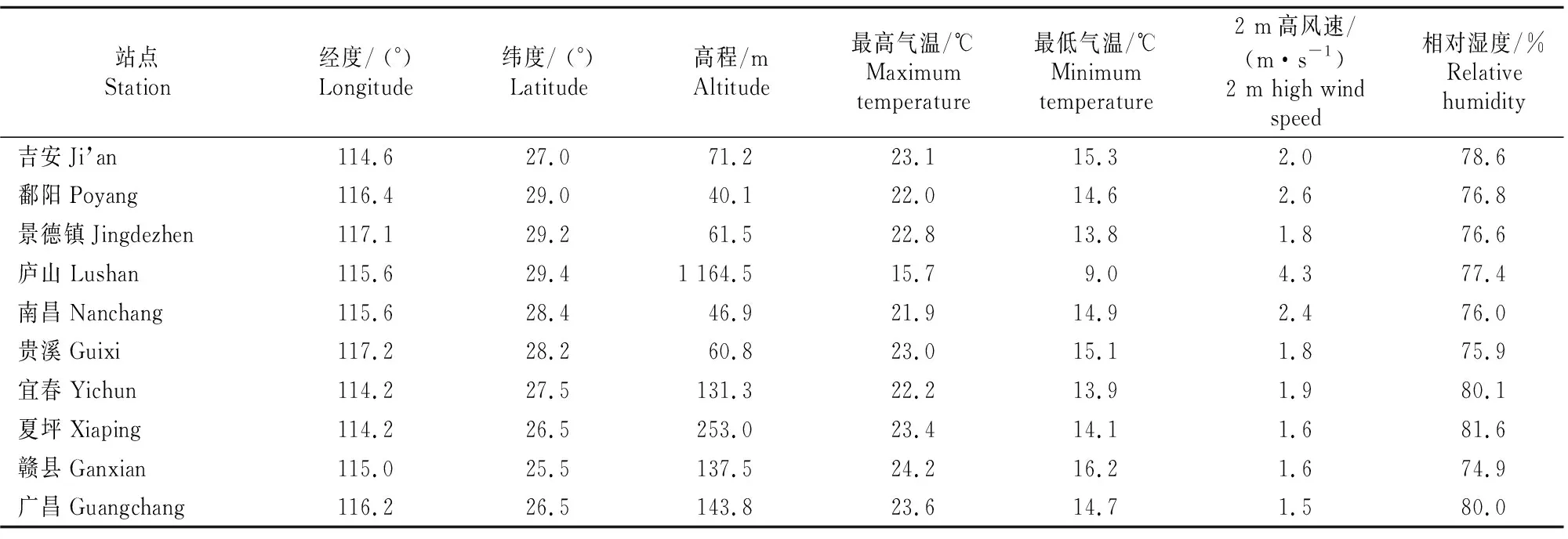
表1 研究所涉及气象站点的基本信息Table 1 Basic information of related weather stations

所使用气象资料均由中国气象数据共享服务网提供，数据经严格把控，质量较好。本研究使用K折交叉验证法进行测试，将观测数据的数据集均分成4等份，取其中3份训练模型，剩下1份用于模型测试。该过程重复4次，每次使用的测试数据应有区别。

1.3 研究方法

1.3.1 支持向量机(SVM)模型 SVM是近年国际上开始流行的一种新型处理非线性分类和回归的有效方法，其以Vapnik等[20]提出的统计学习理论为基础，借助核函数将样本空间映射到一个更高维特征空间。在特征空间中将寻求最优回归超平面问题归结为一个约束条件下的凸二次规划问题，从而求得最优解。与常用神经网络模型相比，SVM由于最优化问题是凸函数，因此可以得到一个全局最优解[21]。

首先假设存在某个线性问题，其数据集H可表示为：

(1)

式中：xi为输入变量，di为目标值，i=[1,2,…,n]，n为数据量。

则存在以下关系：

f(x)=ωφ(x)+b。

(2)

式中：ω为权重，φ(x)为高维超平面函数，b为偏差。ω和b可由结构风险最小化来确定。

可见，该问题转换为凸二次规划问题，当存在唯一最小值时，引入拉格朗日乘子，则式(2)还可表示为：

(3)

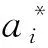
1.3.2 极限梯度提升法(XGBoost)模型 XGBoost是梯度提升机(GBMs)的一种新模式[22]，其通过对决策树算法的优化，改进了对数据库的处理，通过正则化和内置交叉验证来解决过拟合问题，从而提高了计算精度并可以保持最佳计算速度。此外，在训练期，XGBoost模型中的函数将自动运行并进行计算，因而在特征提取[23]、分类[24]和估算[25]等方面被广泛应用。XGBoost模型是源于“提升”的概念，其结合了一组所有弱学习者的预测，通过特殊训练培养强学习者[26]。其表达方式如下：

(4)

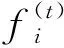
为了在不影响模型计算速度的情况下防止过拟合问题，XGBoost模型可推导出以下公式：

(5)

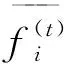
(6)

式中：β和λ为正则化系数，T为叶子节点个数。

1.4 FAO-56 PM模型

采用FAO-56 PM模型[27]计算吉安站和鄱阳站的ET0值，计算公式如下：

(7)

式中：Rn为地表净辐射(MJ/(m2·d))，G为土壤热通量密度(MJ/(m2·d))，γ为温度计常数(kPa/℃)，Tmean为2 m高处的平均气温(℃)，es和ea分别为饱和水汽压与实际水汽压(kPa)，Δ为蒸汽压曲线的斜率(kPa/℃)。

1.5 统计指标

选择决定系数(R2)、均方根误差(RMSE)、平均偏置误差(MBE)和归一化均方根误差(NRMSE)4个常用统计指标，分析和比较不同模型估算ET0月值的精度和稳定性。其数学方程式分别为：

(8)

(9)

(10)

(11)

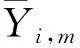
衡量标准为：R2值越高(即越靠近1)，表明模型性能越好，回归曲线与数据拟合越好。相反地，RMSE、NRMSE值和MBE值的绝对值越低，说明模型性能越好。

2 结果与分析

2.1 本地输入气象组合下模型估算性能的比较

为评估SVM和XGBoost模型在本地数据输入模式下估算ET0的适用性，表2，3分别列出了吉安站和鄱阳站在8种输入参数组合下(依次对应记为模型SVM1～SVM8和XGBoost1～XGBoost8)，训练期和测试期估算ET0的各统计指标的计算结果，其中最佳值以粗体标出。

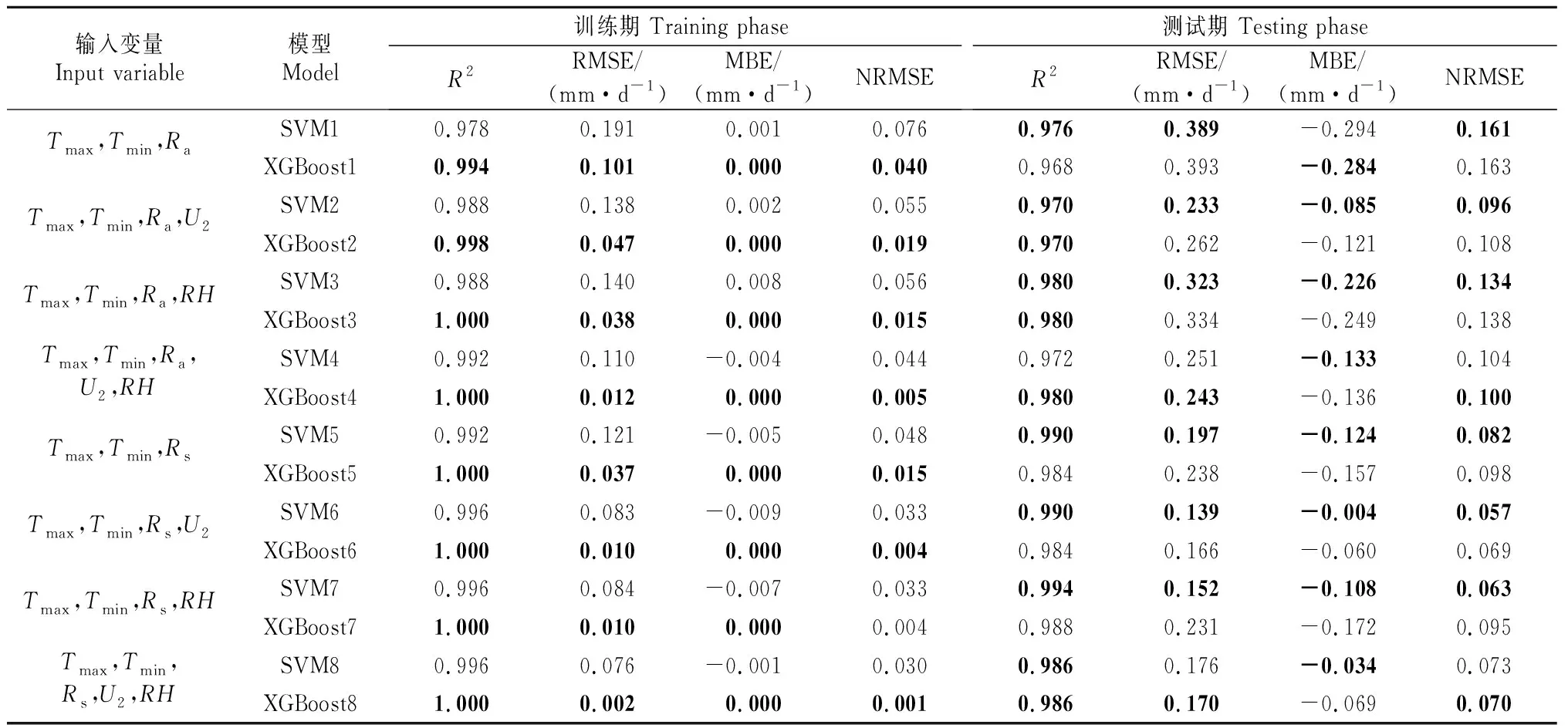
表2 吉安站两时期8种输入参数组合下各模型不同统计指标的比较(本站输入数据)Table 2 Comparison of different statistical indicators of each model under eight combinations of input parameters in two phases of Ji’an station (local input data)

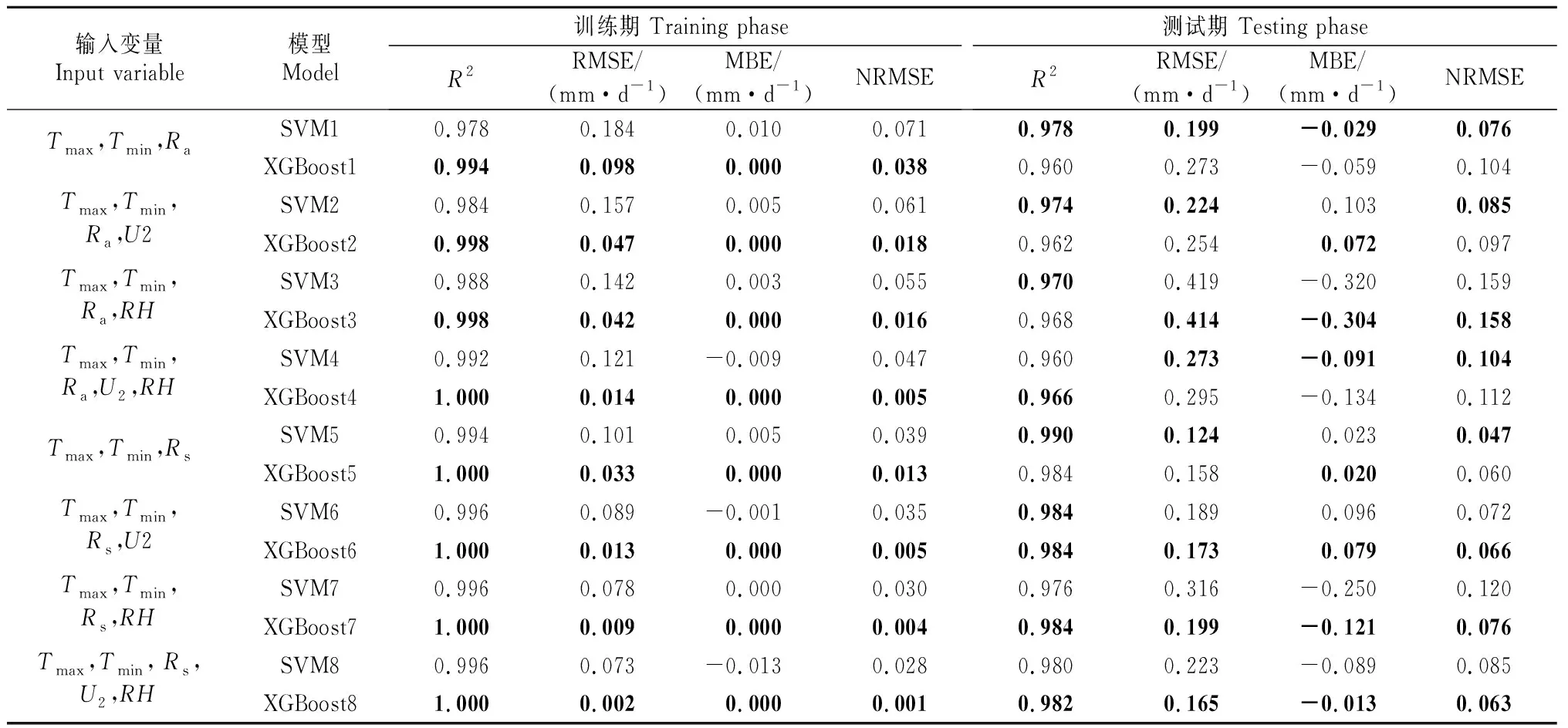
表3 鄱阳站两时期8种输入参数组合下各模型不同统计指标的比较(本站输入数据)Table 3 Comparison of different statistical indicators of each model under eight combinations of input parameters in two phases of Poyang station (local input data)

表2，3显示，在吉安站的测试期，SVM7性能最佳，XGBoost1表现较差，但其参数种类及资料少，且易获取。从MBE值来看，SVM1和XGBoost1被严重低估。在鄱阳站的测试期中，SVM3和XGBoost3也被严重低估，说明输入参数不足使得模型估算精度较低且稳定性较差。由表2和表3还可知，在吉安站的测试期中，XGBoost5的估算性能优于XGBoost1，其中R2值增加1.7%，RMSE值下降了39.4%，说明输入气象因子Rs较Ra更能提高模型的估算性能，此规律在鄱阳站也存在。XGBoost6的性能优于XGBoost5，可知增加输入参数U2能提高模型的估算性能，这可能是因为风速对ET0的平流效应所致。表3显示，SVM6的估算性能整体优于SVM8，说明增加输入参数RH反而降低了模型的估算性能，可能是由于RH因子的影响因素过多，使得其变化差异较大所致。

以吉安站点为例，图2为本地输入条件下SVM和XGBoost模型的散点图。图2显示，SVM2和XGBoost1的R2值较低，且散点分布偏离拟合线；SVM7和XGBoost7中各散点的分布均紧贴拟合线，且优于SVM8和XGBoost8的精度，说明参数增多会导致影响因素增加，反而影响模型的估算性能。SVM5和XGBoost5的估算精度较高，性价比最高。综上所述，当输入本地数据时，各模型在估算ET0时均有较好表现，此时最实用的输入组合是Tmax、Tmin、Rs，而且结合两个时期可知，XGBoost的性能整体上略优于SVM模型。

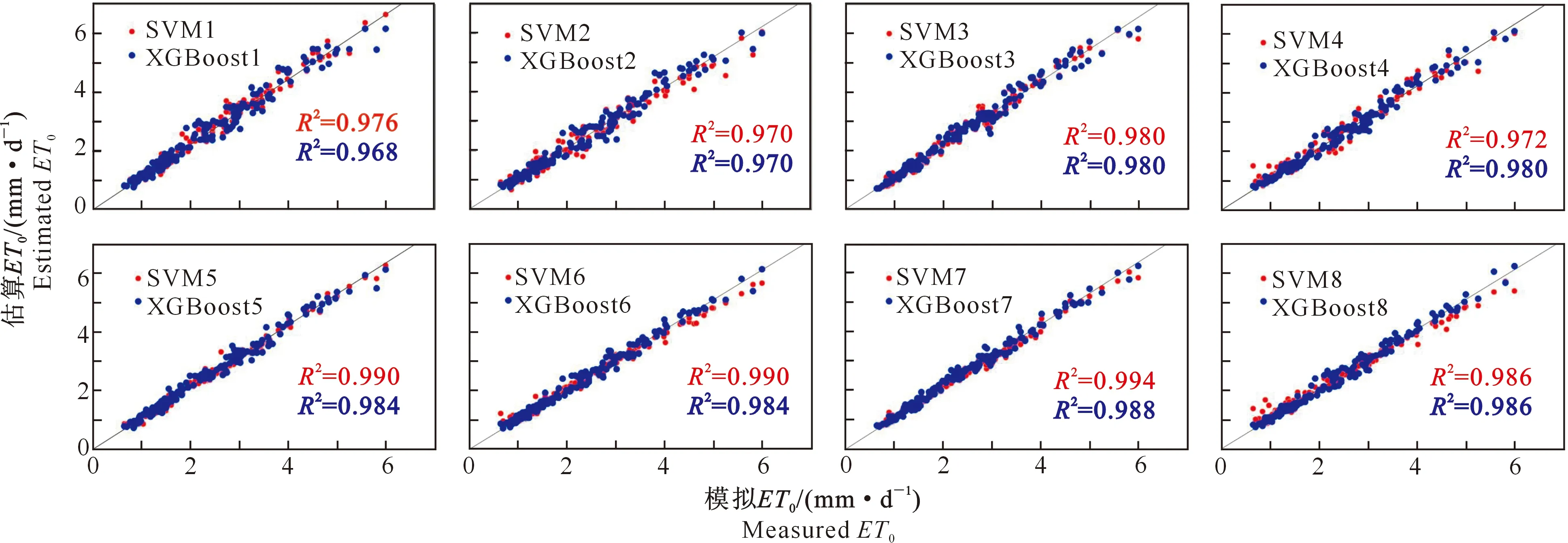
图2 测试期吉安站ET0模拟值与估算值的散点图(本地输入)Fig.2 Scatter plot of measured and estimated values of ET0 at Ji’an station during testing phase (local input data)

2.2 邻站与本地数据结合情况下模型估算性能的比较

在本地融合邻站气象数据的9种输入参数组合模式下(依次对应记为模型SVM9～SVM17和XGBoost9～XGBoost17)，分别对各输入模型估算ET0的适用性进行评估，得到吉安站和鄱阳站各模型估算ET0的各统计指标的计算结果见表4和表5。

表4 吉安站两时期9种输入参数组合下各模型不同统计指标的比较(本站结合邻站数据)Table 4 Comparison of different statistical indicators of each model under nine combinations of input parameters in two phases of Ji’an station (local and cross-station data)

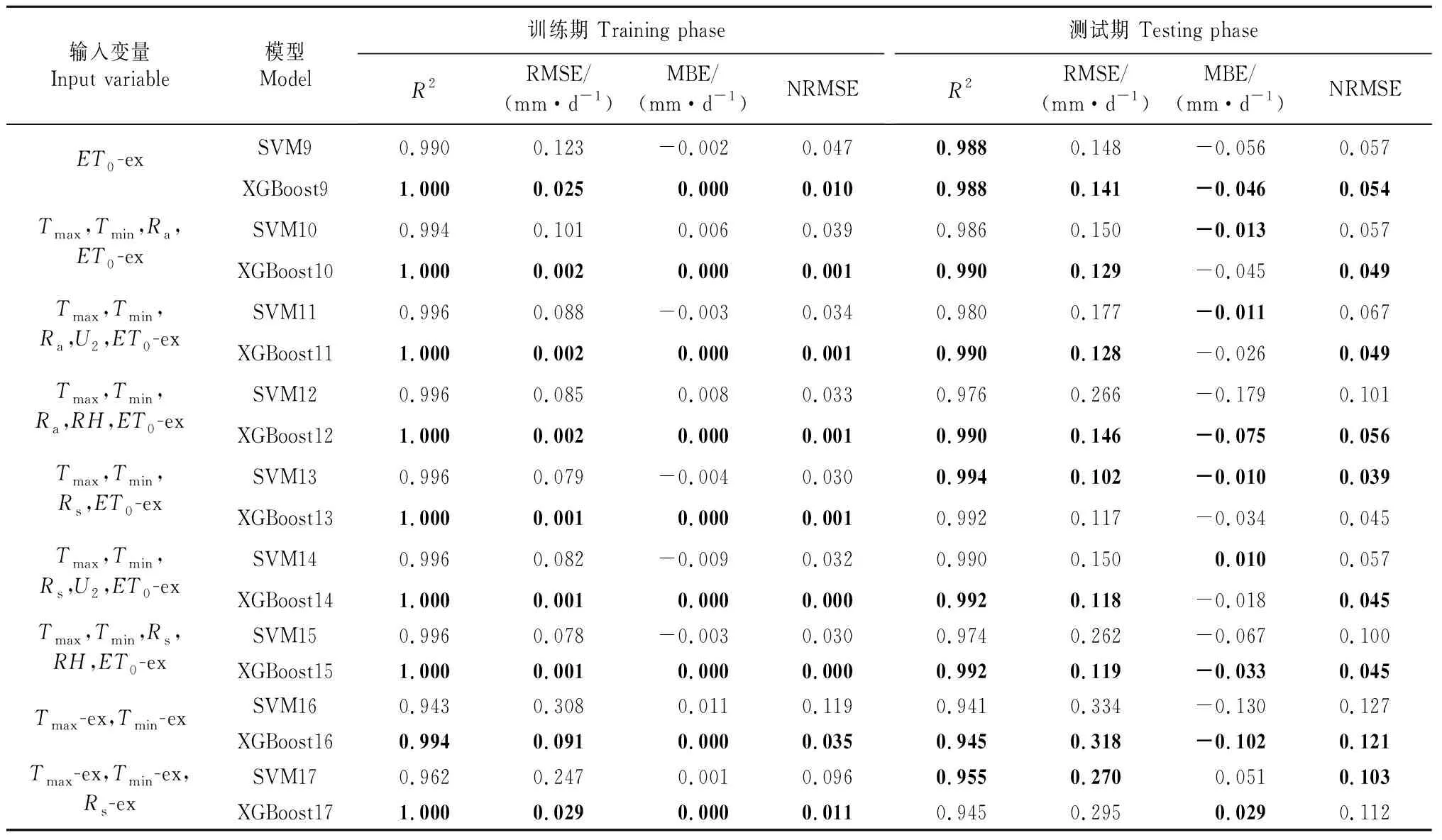
表5 鄱阳站两时期9种输入参数组合下各模型不同统计指标的比较(本站结合邻站数据)Table 5 Comparison of different statistical indicators of each model under nine combirations of input parameters in two phases of Poyang station (local and cross-station data)

表4显示，在吉安站的测试期中，除XGBoost16和XGBoost17外，XGBoost9～XGBoost15的估算性能差异较小，其R2为0.982～0.990。大部分情况下，输入同种参数组合时，XGBoost的估算性能优于相对应的SVM模型。从表5可以看出，在鄱阳站的测试期中，XGBoost9～XGBoost15的R2为0.988～0.992，而XGBoost17的R2为0.945。该结果说明，只输入邻站的Tmax、Tmin和Rs数据来估算目标站点的ET0，虽具有可行性，但无法获得较好的估算性能，可能是因为多个相邻站点之间的参数数据差异较大导致模型估算精度较低。在吉安站的测试期中，只采用ET0-ex作为输入参数的SVM和XGBoost模型依然表现出较好的性能，其平均R2为0.978，RMSE接近或等于0.250 mm/d，此时所需气象资料最少且易获取。

以吉安站为例，图3绘制了数据融合模式下2种模型的散点图。从SVM9和XGBoost9的散点分布情况可知，该模型拟合程度良好，且XGBoost9的估算性能优于XGBoost16和XGBoost17。而SVM14和XGBoost14的散点分布紧贴拟合线，拟合程度最好。另外，XGBoost11的散点分布较XGBoost10更靠近拟合线，分布更均匀,所以准确选取合适的参数组合对ET0的估算至关重要。综上可知，当输入本地融合邻站气象数据时，各模型可成功估算目标站点的ET0，且具有较好表现。但只采用气象因子ET0-ex作为输入参数时性价比最高，而且XGBoost9的性能优于SVM9。

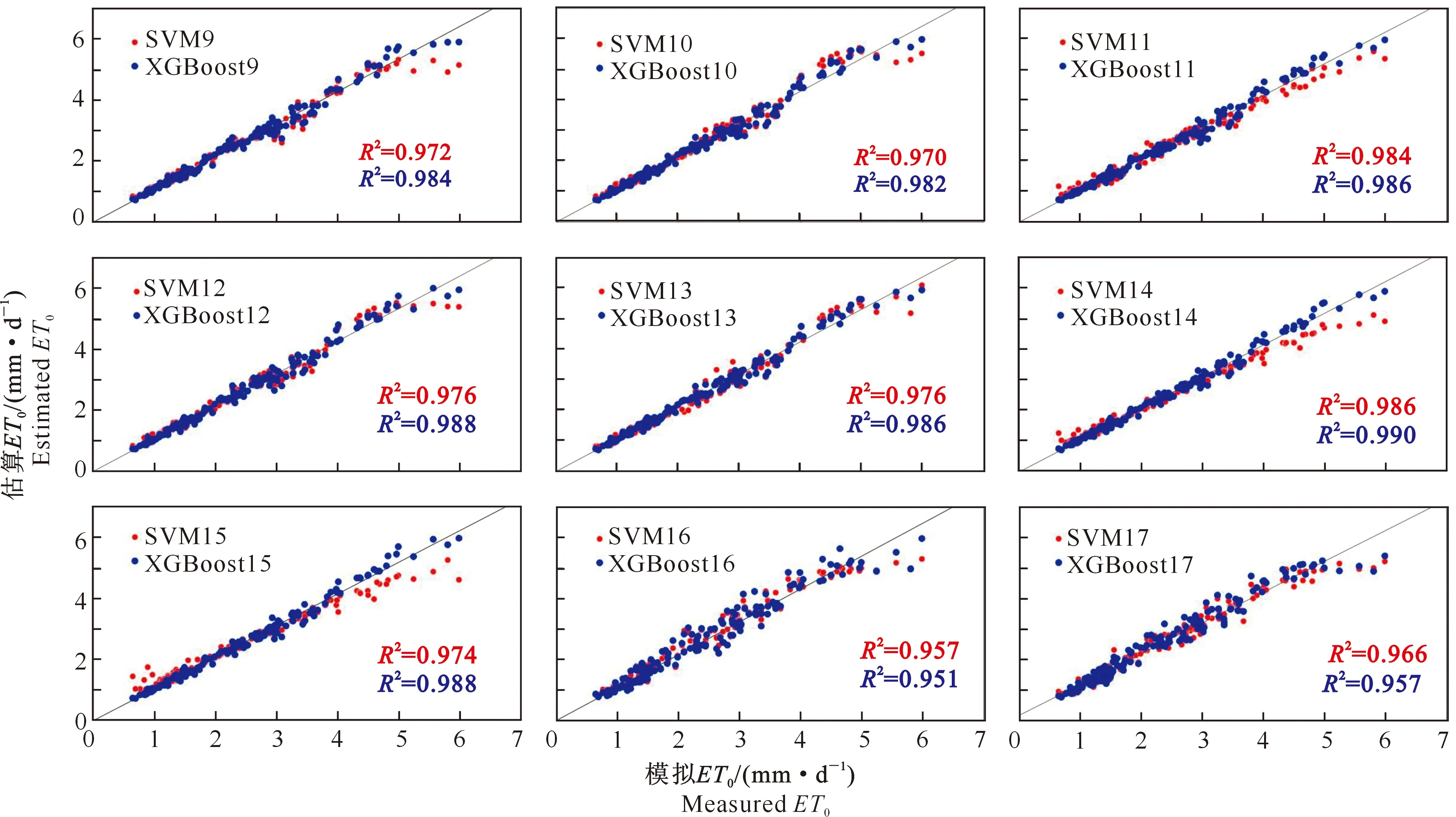
图3 测试期吉安站ET0模拟值与估算值的散点图(本地与邻站数据结合)Fig.3 Scatter plot of measured and estimated values of ET0 at Ji’an station during testing phase (local and cross-station)

2.3 2种机器学习模型综合性能的比较

以吉安站为例，对2种机器学习模型(SVM1～17和XGBoost1～17)在不同输入参数条件下的估算性能进行综合分析，并绘制由FAO-56 PM模型计算的ET0及SVM和XGBoost模型测试期所估算ET0差值的箱线图，结果见图4。从图4可以看出，以ET0差值的中位值来看，各模型表现存在偏差，其中SVM1、SVM3、SVM10、SVM16、SVM17、XGBoost1和XGBoost3对ET0的估算偏差较大，SVM6、SVM8、SVM14、XGBoost6和XGBoost8的表现较为稳定。从四分位线来看，除SVM1、SVM3、XGBoost1、XGBoost3、XGBoost16和XGBoost17外，其他模型之间差异较小。在极值方面，SVM1所模拟极小值效果不佳，SVM7表现最优；而XGBoost模型均能模拟出标准极值，其中以XGBoost6整体表现最为稳定，各种误差值均较稳定地接近于0。本地融合邻站气象数据作为输入时，各模型性能较本地输入时略显稳定，但前者所需数据集更多。

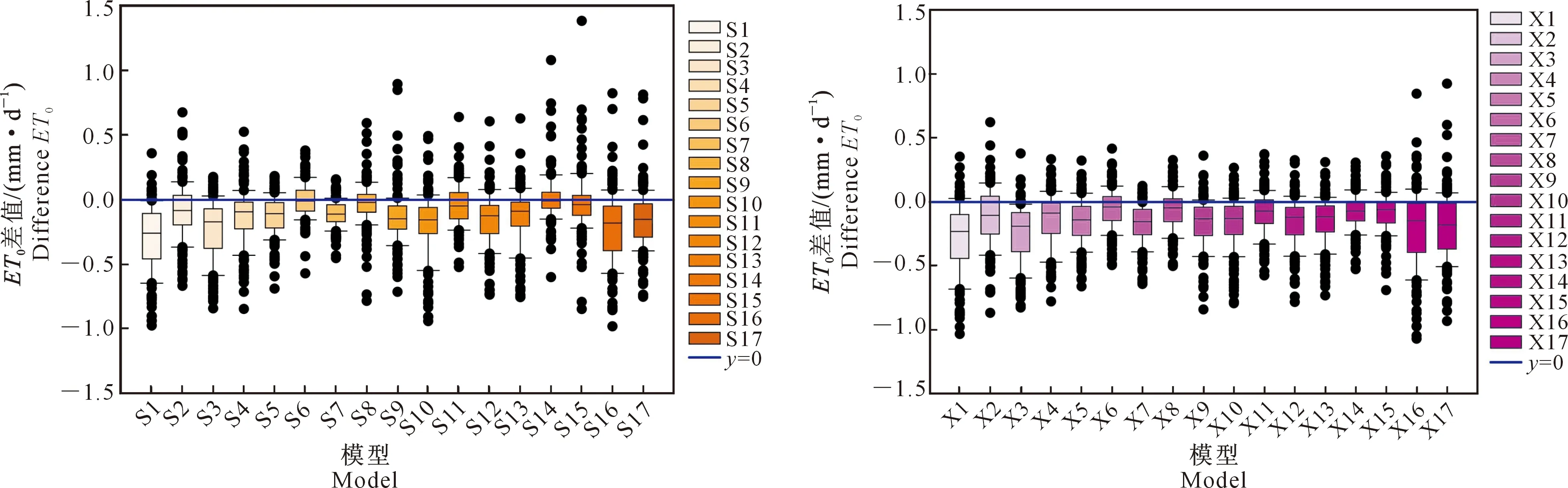
S1～S17分别表示模型SVM1～SVM17，X1～X17分别表示模型XGBoost1～XGBoost17。图5同S1-S17 represent SVM1-SVM17 models,X1-X17 represent XGBoost1-XGBoost17 models.The same for Fig.5

图5绘制了吉安站各模型RMSE值的变化情况。图5表明，在训练期，XGBoost模型在对应组合下的稳定性均优于SVM模型，且XGBoost10～XGBoost15的稳定性较XGBoost16和XGBoost17更优，RMSE更接近于0。但在测试期，各模型的RMSE值均显著增加，存在过度拟合问题。SVM模型中，SVM6和XGBoost6的稳定性最佳，且两者稳定性相差不大。采用Tmax、Tmin、Rs作为输入参数时RMSE值较低。另外，XGBoost模型的数据处理速度优于SVM模型，计算时间较SVM模型少。根据散点图、箱线图和柱状图所表现出来的结果，综合评估XGBoost和SVM模型在2种输入模式下估算ET0的精度和稳定性等，表明使用本地结合邻站气象资料估算目标站点ET0月值具有可行性，且推荐使用XGBoost模型，且2种输入模式下最实用输入组合分别为组合Tmax、Tmin、Rs和ET0-ex。

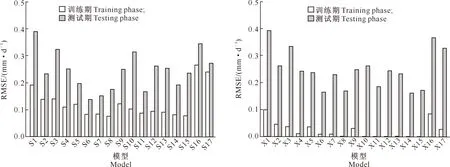
图5 2种机器学习模型测试期和训练期RMSE值的比较(吉安站)Fig.5 Comparison of RMSE values of two machine learning models during testing and training phases (Ji’an station)

3 讨 论

Fan等[28]针对中国不同气候区，评估了SVM和XGBoost等模型估算ET0的潜力，发现XGBoost模型的估算性能优于SVM模型。本研究针对江西鄱阳湖地区，使用同一气候区内本地气象资料及本地和多个邻站ET0等气象资料结合的两种模式，用SVM和XGBoost 2种模型估算ET0，结果表明，在大多数参数组合输入条件下，XGBoost模型的精度和稳定性优于SVM模型，与前人的研究结论[29]相一致。已有学者使用邻站数据来估算目标站点ET0的报道，如Kisi[16]评估了MARS和M5 Tree等模型在土耳其使用邻站数据估算ET0的潜力，发现在缺乏本地输入和输出情况下，以MARS模型性能较好。Fan等[30]在江西地区使用其他15个站点数据估算井冈山站ET0时发现，M5 Tree模型的测试期估算精度较训练期提升了1%，与低海拔站点估算结果差异较小。Wu等[17]在江西地区使用庐山站与鄱阳湖流域站点进行换站研究，得出MARS模型估算性能具有较高的稳定性，说明在同一气候区，不同海拔站点在换站估算ET0研究中对模型的估算性能影响较小。另外，针对本研究站点间距离因素而言，Lu等[31]在鄱阳湖流域估算ET0时的研究表明，RF和M5 Tree模型的RMSE值随着换站站点间距离增加而增大，但所得估算精度较好，说明本研究选取的各站点的换站距离具有合理性。

Citakoglu等[32]和Mehdizadeh等[33]进行了不同模型在不同区域估算ET0的研究，表明增加气象因子U2能提升模型的估算性能，与本研究所得结论一致。输入单一风速参数时模型估算精度不高，但与温度、辐射等结合，可提高模型估算精度。此外，地表总辐射Rs是估算江西鄱阳湖地区ET0的最关键气象因子，这与Fan等[28]在中国武汉站和广州站及Feng等[15]在四川地区的研究结果相似。然而，Mattar[34]在埃及进行的ET0估算研究发现，U2是最重要的气象因子，将其添加到基于温度的估算模型中，所得RMSE值可从10.20 mm/d降到0.58 mm/d。但本研究表明，添加Rs数据仅可略微提高ET0估算精度，出现该差异的原因，可能与估算ET0的主要气象变量及其对ET0的影响在不同区域间存在差异有关[35]。

常规经验模型仅需少量气象数据就可获得较高的ET0估算精度，但仍存在估算性能被高估或低估的现象[36-37]。本研究表明，SVM和XGBoost模型在江西省吉安站和鄱阳站ET0估算运用中，存在一定程度上的低估现象。这可能是由于测试期的平均温度较训练期有所提高，使得ET0增大，导致模型存在低估现象。ET0受气候影响较大，冯禹等[38]使用不同模型对四川中部不同区域的ET0进行了估算，结果表明地理、人类活动等因素会对ET0的估算产生差异性影响，但在同一气候区仍可以进行换站研究。

4 结 论

1)在江西鄱阳湖地区，使用本地气象资料来估算ET0时，综合测试期和训练期2个时期来看，XGBoost模型的性能略优于SVM模型。采用Tmax、Tmin、Rs作为输入参数时，其估算性能的性价比最高，测试期R2值均大于0.98。因此在使用本地气象资料估算ET0时，在江西地区推荐使用XGBoost模型。

2)将本地与邻站数据相结合，可成功估算目标站点的ET0值，此时推荐使用XGBoost模型，且只采用气象因子ET0-ex作为输入参数时性价比最高，即数据量最少且估算性能高，R2值均大于0.97。因此，在本研究中的同一区域或其他相类似条件的气候区中，当部分站点缺少正常气象资料时，可将本地与邻站数据相结合，使用XGBoost模型来估算ET0。

3)选择合理的气象因子组合对ET0的准确估算十分重要。Tmax和Tmin是估算ET0研究的最基本因子，增加U2因子会略微提高研究模型的估算性能，因子Rs的重要性高于RH，但增加输入多余低效因子会使模型运算量加大从而降低模型的估算性能。因此，本研究推荐使用XGBoost模型来估算ET0，且2种输入模式下推荐输入组合分别为Tmax、Tmin、Rs和ET0-ex。

在本研究中，仅使用几种常规气象因子作为输入，且运用了邻站ET0等气象资料，之后的研究可进一步引用其他气象因子，如日照时数、降雨量等，分析其对模型估算ET0的影响。另外，还需要研究站点间距离、所属省份和气候对模型适用性的影响。此外，还可以开发一些新混合机器学习模型，比如使用粒子群算法(particle swarm optimization，PSO)来优化SVM，或将2种模型进行耦合，以获得更高的ET0估算精度。