希帕索斯悖论与无理数
2021-09-10林革
林革

说到希帕索斯悖论,首先要提到的是毕达哥拉斯学派和毕达哥拉斯定理.
毕达哥拉斯是一位与孔子、释迦牟尼几乎同时代的古希腊著名数学家和哲学家. 他创办了一个著名的学派——毕达哥拉斯学派,其宗旨是“万物皆数”.
毕达哥拉斯学派认为:世界上的万事万物都可以用数来表示,一切事物都由数构成. 无论什么事物,大到天体,小到尘埃,都有一定的长短、高低、大小、轻重等数量,没有数量的事物是不存在的. 总之,一切事物都必须而且只能通过数得到解释,宇宙的本质和规律就是数的和谐,也就是说,宇宙间的一切现象都能归结为整数或整数之比. 显然“万物皆数”中的数就是有理数.
毕达哥拉斯定理就是著名的勾股定理,即直角三角形斜边的平方等于两直角边平方之和. 据说毕达哥拉斯发现这个定理有一段有趣的渊源.
有一次,毕达哥拉斯被邀请到朋友家做客,客人们高谈阔论,他却一言不发,静静地坐在那里. 他本来就是一个沉默寡言、不爱凑热闹的人,平时除了思考数学问题和别人沟通交谈外,没有任何别的事情能让他多费口舌. 毕达哥拉斯一直低头看地上铺的花砖(花砖形状如图1),屋里没人感到奇怪.
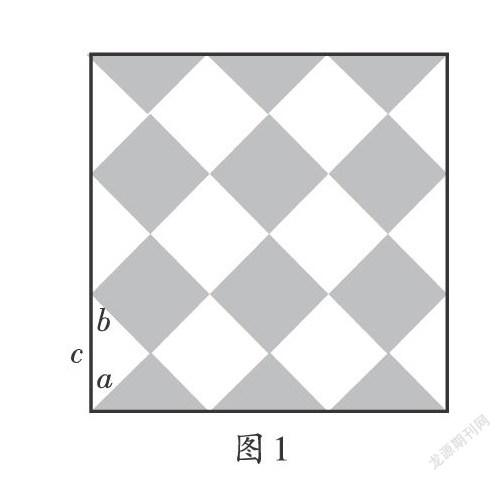
花砖上的图形有正方形和三角形,黑白相间且有规律地排列着,这好像没什么特别的,可毕达哥拉斯竟被这个司空见惯的图案吸引住了. 他几乎忘记了自己是来做客的,竟弯下腰去,在靠边的花砖上算了起来.
毕达哥拉斯在直角三角形的一条直角边上写上a,另一条直角边上写上b,在斜边上写上c(如图1). 以a为边的正方形面积a2恰好等于两个灰色三角形面积的和,以b为边的正方形面积b2恰好等于两个白色三角形面积的和,以c为边的正方形面积c2恰好等于两个灰色三角形与两个白色三角形面积的和,即c2 = a2 + b2. 由此,毕达哥拉斯得出結论:以c为边的大正方形面积等于以a或b为边的两个小正方形面积的和.
毕达哥拉斯和他的门徒在给出这条定理的证明后欣喜若狂,宰了100头牛,举办了盛大的“百牛宴”以示庆贺. 因此,勾股定理也被称为“百牛定理”.
不过,具有讽刺意味的是,毕达哥拉斯定理的发现和证明导致毕达哥拉斯学派的宗旨被动摇了.
毕达哥拉斯学派中的一个青年弟子希帕索斯,在研究正方形的对角线时发现,这条对角线既不能用整数表示,也不能用整数之比(分数)表示. 因为,如果能用整数或整数之比表示,则必然带来不可克服的矛盾. 具体推导如下:
假设正方形的边长为1,如图2,
则根据勾股定理可知斜边w2 = 12 + 12 = 2,这个w一定不是整数,
因为12 = 1,22 = 4,
而12 < w2 < 22,
又因为1和2是两个连续的自然数,
所以w只能是夹在1和2之间的分数.
假设这个分数为[mn],
必须说明该分数是既约分数(m,n已经约去了所有的公因数),
可得结论:m,n之中至少有一个奇数(若两者都是偶数,则存在公因数2,这与前提假设矛盾).
∵[m2n2] = 2, ∴m2 = 2n2.
又∵2n2为偶数,∴ m2为偶数,
如果m为奇数,那么m可以表示成2p + 1,
则m2 = (2p + 1)2=4(p2 + p) + 1也是奇数,这与上面得到的m2为偶数矛盾.
∴m必为偶数.
又∵m,n二者中至少有一个奇数,m必为偶数,
∴n必为奇数.
m为偶数,可设 m=2p,即m2=4p2=2n2,得n2=2p2,
也就是说n2为偶数,则n必为偶数. 这又与上面得到的n必为奇数矛盾.
不难看出,同一个数n既是奇数又是偶数.
但是我们都知道,一个数要么是奇数,要么是偶数,不能既是奇数又是偶数.
因此,以上循环必然产生矛盾,人们把这种循环称为希帕索斯悖论.
推导过程之所以出现矛盾的结论,无外乎以下两种原因:一种是前提错误,一种是推导过程错误. 以上的推导过程中使用了两个前提:一个是毕达哥拉斯学派“一切现象可归结为整数或整数之比”的信念,另一个就是毕达哥拉斯定理. 然而,由二者都推出了矛盾.
显然,上述推导过程毫无差错,那么问题只能出在前提上. 毕达哥拉斯定理是已证明为正确的定律,这样只能说明毕达哥拉斯学派的信念不成立. 希帕索斯悖论的发现如同一声晴天霹雳,动摇了毕达哥拉斯学派整个信念大厦的基础,引起了学派极大的恐慌,以至于希帕索斯最终为了真理付出了生命的代价.
然而“青山遮不住,毕竟东流去”,人们又发现了其他不能用整数或整数之比表示的数,如[3],[5],[7],[π]等,如今这些无理数已经被大众普遍接受.
虽然希帕索斯被抛到大海里淹死,但希帕索斯悖论是淹不死的. 这些事实像潮水一样猛烈地冲击着传统观念,促使人们重新审视“一切数都是整数或整数比”的有理数理论,这就是历史上的第一次数学危机. 当然,从本质上严格来说,这种危机并不是数学本身的危机,而是毕达哥拉斯学派“万物皆数”(整数或整数之比)信念的危机.
(作者单位:扬州职业大学)
