STEM理念下中职建筑类专业数学课程内容重构的实践研究

张明琦 颜伟

[摘           要]  随着时代的不断发展，社会对技术型人才的需求也在逐年增多，中职学校作为技术型人才的主要培养阵地，其在教育中的地位得到了有效提高。STEM理念在中职数学教学中的应用，打破了学科之间的独立性，将日常教学与学生的专业有机结合起来，促进了技术型人才的培养。立足于STEM理念，结合中职数学教学案例，简要分析了建筑类专业数学课程内容的重构策略，以供大家参考。

[关    键   词]  STEM理念;中职数学;建筑

[中图分类号]  G712                 [文献标志码]  A            [文章编号]  2096-0603（2021）25-0132-02

一、关于STEM教育理念

与传统的教学方式相比，STEM教育理念在学科教学中的应用打破了学科之间的壁垒，将各个领域的知识进行了综合整理，为学生提供了更加丰富的学习体验，也在一定程度上推动了教学改革的步伐，主要体现在以下几个方面：（1）课堂学习氛围、教学模式等，都由封闭走向了开放，学生掌握知识的灵活性有了明显提高。（2）由单独的一门学科走向了融会贯通，有力地提高了学生的知识迁移能力。（3）由单打独斗走向了合作学习。在STEM教育理念下，学生的合作意识、团队意识有了显著提升，学生的课堂学习效率也有了质的飞跃。（4）由被动学习走向了主动学习。在该教育理念的影响下，教师所营造的课堂氛围更具趣味与活力，学生会主动去探究、思考问题，有效地促进了学生综合学习能力的提高。（5）由重知识讲解走向了重问题解决。在以往的教学模式中，学生大多存在“高分低能”的学习状况，而STEM教育理念更侧重于培养学生的知识应用能力，为学生的长远发展打下坚实的基础。由此可以看出，STEM教育理念在中职数学教学中的应用，不仅能够提高学生的学习能力，还能够提高学生的综合素养。

二、STEM理念下中职建筑类专业数学课程内容重构的策略

（一）借助多媒体技术，发挥STEM理念在数学教学中的设计性

多媒体技术与教学的融合应用，似乎已成为教师在教学中常用的方式之一。而这种教学模式在STEM教育理念的干预下，增添了更多富有设计性的元素，对促进学生知识迁移能力的提升有极大的帮助[1]。对于中职建筑专业的学生来说，数学学科中的很多知识都与自身的专业相关，在解决建筑专业的相关问题时，会运用到很多所学的数学知识。

例如，在学习直角三角形的应用一部分内容时，教师可以在教学前，对建筑专业学生的学习进度做一些小调查，结合学生的专业学习情况，有针对性地设计数学教学内容。根据了解，数学教师能够发现，学生已经学习了建筑力学的基础内容。本节三角形相关知识内容的讲解，实则是在帮助学生巩固已学三角形知识的同时，颠覆学生认为“数学无用”的观点，使学生切实感受到数学知识与建筑专业之间的紧密联系。在上课之初，教师可以借助多媒体将楼梯的图片呈现给学生，并向学生明确本节内容的学习任务：利用相似三角形计算楼梯楼板各条支座负筋的长度。紧接着，教师可以借助多媒体的动画效果，将该楼梯的剖面简要图展示出来，鼓励学生计算底筋斜长的长度。通过对图片的观察，学生能够发现：楼梯剖面图是直角三角形，结合已知的数据，并运用勾股定理，就能够计算出底筋斜长的数据。教师借助多媒体技术，构建具有设计性的数学课堂，帮助学生解决了建筑课上的问题，有效地提高了学生的课堂学习质量。

（二）基于小组合作，发挥STEM理念在数学教学中的协作性

中职数学教师在实际的教学活动中，若是想充分发挥STEM教育理念的价值，就需要强调群体协同中相互帮助、相互启发的作用，鼓励学生进行合作学习，培养学生的团队意识与合作能力[2]。也就是说，数学教师在开展课堂教学时，应设计一些與建筑专业相关的实际问题，鼓励学生通过共同配合、探讨去解决这些问题。在这一过程中，学生不仅能够掌握数学学习内容，还能够对建筑专业知识有更为全面的了解。在具体的教学安排中，中职教师需要先对学生的学习情况进行了解，再按照一定的原则对学生进行分组，保证各个小组之间的整体学习水平是相同的，且组内的各个成员能够取长补短，达到提升学生数学学习水平的效果。

例如，在学习余弦定理的应用一部分内容时，中职教师既要考虑到数学课程其本质的特点，又要考虑到其与建筑专业知识间的联系。据调查数据显示，在部分数学教材中，并未将“余弦定理”作为单独的教学部分，但在建筑测量中却用到了余弦定理。针对这种情况，数学教师应重视余弦定理教学的重要价值，鼓励学生通过小组合作来学习这部分内容。在讲述完理论部分的内容后，教师可以向学生提出实际问题，要求学生通过合作互助来解决以下问题。

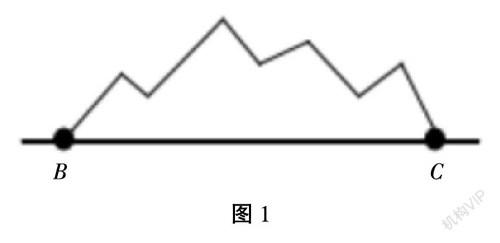
某建筑企业承包了高铁建设项目，在进行高铁路线的规划工作时遇到了问题。铁路会经过一座小山丘，如图1，这就需要挖隧洞。但是施工队伍无法直接测量两山脚之间的距离，如果要知道山脚B、C之间的距离，需要通过什么样的办法来解决？

在学生针对问题开始讨论时，教师可以为学生提供一些提示：此问题可以转化为知道三角形的两边与夹角，借助余弦定理求第三边的问题。通过教师的指导、学生之间的合作探讨，小组能够得出计算方式：工作人员可以在平地上任意选出一点A，绘制出一个三角形ABC，借助工具分别测量出AB、AC的长度，并量出两条边的夹角度数，最后结合余弦定理计算出BC的长度。在课前对学生的学习能力进行调查了解，在课上教学时结合建筑专业知识，为学生布置合作学习的任务，引导、鼓励学生运用余弦定理解决问题。在这一过程中，学生能够真正学会借助数学知识解决问题，使学生体会到学好数学对学好专业课的重要作用，让他们重新认识到数学知识的价值。