压缩干粮硬度测试条件的建立与优化

耿战辉，陈蕊君，李志强，马秀玲

（军事科学院系统工程研究院军需工程技术研究所 北京 100010）

物性测试仪主要用于食品、药品、化工产品等的质地与流变性质分析测试[1-3]，通过统一设定的方法，将产品的物性特点通过量化的数据表述[4]，是较为客观、准确的品质测量仪器[5-7]。其测定食品硬度的基本原理是通过模拟人口腔咀嚼运动，利用力学方法模拟食物的质地属性[8]。测试探头以稳定速率下压、穿透或拉伸样品，感受阻力的变化，通过计算得到样品质构特性数值[9-11]。

压缩干粮因体积小、能量密度高、运携便利、使用安全等突出特点[12-13]，而一直是军用食品体系中的骨干产品[14]。然而，由于压制后结构致密、质地硬实，因此干硬是影响压缩干粮食用接受性的主要因素，硬度也始终是评价压缩干粮品质的关键指标[15]。现有文献中，对压缩干粮硬度的研究主要集中在贮存期预测试验和配方优化等方面[16-17]，没有专门针对测定方法建立和优化测试条件方面的研究。普遍缺乏对硬度测试条件的精确设定依据，不同研究中因测试方式和条件参数不同，而导致结果离散度大，稳定性和准确性差[18-21]，对产品品质改进缺乏参考性。

针对上述问题，本文利用物性测定仪三点弯折探头对压缩干粮的硬度进行系统试验，分析各相关参数对硬度测定结果离散度的影响。采用响应面法筛选出最优条件，建立一套离散度小、稳定性高、重现性好的测试条件参数，为压缩干粮品质改进及相关研究提供科学依据。

1 材料与方法

1.1 材料与仪器

13 压缩干粮，秦皇岛福寿食品有限公司提供，产品尺寸：41 mm×82 mm×17 mm（±2 mm）。

物性测定仪 （TA.XT.PLUS、HDP/3PB 探头），英国Stable Micro Systems 公司。

1.2 试验方法

1.2.1 基本操作流程 设定仪器测试条件，将样品支撑架固定于探头正下方，待测样品置于支撑架中心处，使HDP/3PB 探头正对样品。记录并绘制测试过程中的作用力变化曲线，纵坐标为力，横坐标为时间或位移；记录完整曲线中的最大力值，即为样品最大弯折力。最大弯折力与支撑架间距的乘积为折断力矩，体现样品折断时受到的临界扭矩。以折断力矩表征样品的断裂强度或硬度。

1.2.2 支撑架最优间距筛选试验 前期研究工作表明，支撑架间距对硬度测试结果影响明显，为此本文首先对该参数进行了优化筛选试验。设置仪器基本测试条件（模式：下压；操作：返回开始；测试前速度：1.0 mm/s；测试速度：1.0 mm/s；测试后速度：10.0 mm/s；测试距离：5.0 mm；触发力：50 g；数据获取率：200 pps），支撑架间距选择5 个水平（40，45，50，55，60 mm），每个水平各进行10 组平行试验，获得折断力矩均数及标准差，以变异系数（CV）来表征折断力矩的离散程度。

1.2.3 其它测试参数筛选试验 采用前述优化确定的支撑架间距，进行其它影响因素的筛选试验。

1.2.3.1 测试前速度筛选试验 设定测试速度1.00 mm/s，触发力50 g，测试距离5 mm；测试前速度分别取 0.25，0.50，0.75，1.00，1.25，1.50，1.75 mm/s。

1.2.3.2 测试速度筛选试验 设定测试前速度1.00 mm/s；触发力50 g，测试距离5 mm；测试速度分 别 取0.25，0.50，0.75，1.00，1.25，1.50，1.75 mm/s。

1.2.3.3 触发力筛选试验 设定测试前速度1.00 mm/s，测试速度1.00 mm/s，测试距离5 mm；触发力分别取10，30，50，70，90，110，130 g。

1.2.3.4 测试距离筛选试验 设定测试前速度1.00 mm/s，测试速度1.00 mm/s，触发力50 g；测试距离分别取1，2，3，4，5，6，7 mm。

1.2.4 响应面法优化测试条件 根据单因素实验结果，以测试前速度、测试速度、触发力3 个因素为自变量，最大弯折力的标准差表示离散度，并作为响应值进行三因素三水平响应面试验，通过Design Expert 10.0.4 软件对试验数据进行回归分析，得到最佳测试条件组合。

2 结果与分析

2.1 样品支撑架间距对折断力矩的影响

调整支撑架间距，测试在不同间距下压缩干粮折断力矩结果的变化情况，结果见表1。

由表1可见，样品支撑架间距对压缩干粮折断力矩的影响显著，数据变化或变化趋势未呈现明显规律性，且变异系数大。支撑架间距为40，45，55，60 mm 时，变异系数分别为23.8%，25.2%，33.7%和17.4%，测定结果的离散程度均较大；只在支撑架间距为50 mm 时，变异系数小于10%，测定结果的离散程度较小，提示在支撑架间距为50 mm 的条件下，压缩干粮硬度测试的稳定性和重现性较好。据此，在其它单因素筛选优化实验中，将支撑架间距设定为50 mm，在此条件下，以最大弯折力作为不同样品断裂强度或硬度比较的表征指标。

表1 支撑架间距对折断力矩测定结果的影响Table 1 Effects of the supporting frame distance on breaking torque

2.2 其它测试参数单因素实验结果

2.2.1 测试前速度实验结果 测试前速度是探头与样品之间的作用力达到设定触发力之前的过程速度。由图1可见，测试前速度对最大弯折力的影响较明显，随着测试前速度的增加，最大弯折力呈先降、趋稳、后升的态势，在0.75～1.25 mm/s 之间相对平稳。提示在此区间，探头施加在样品上的力波动较小，测定数据离散程度较小，结果较为稳定。因此选定测试前速度条件0.75，1.00，1.25 mm/s 进行响应面试验。

图1 测试前速度对最大弯折力的影响Fig.1 Effects of pre-test speed on the maximum bending force

2.2.2 测试速度实验结果 测试速度是当探头接触样品后达到设定触发力时的速度。由图2可见，测试速度对最大弯折力影响显著，数据变化或变化趋势未呈现明显规律性。在前段 （0.25～0.75 mm/s）和后段（＞1.50 mm/s），数据变化幅度大，仅在1.00～1.50 mm/s 范围时，测定数据离散程度较小，结果较为稳定。选定测试速度1.00，1.25，1.50 mm/s 进行响应面试验。

图2 测试速度对最大弯折力的影响Fig.2 Effects of test speed on the maximum bending force

2.2.3 触发力实验结果 触发力是设定的开始进行样品测试和数据记录时的受力值。由图3可见，触发力对最大弯折力影响显著，整体呈现前段（10～50 g）波动幅度大，中后段（＞50 g）趋于稳定的态势，而在中间段（50～90 g）范围时，测定数据离散程度较小，结果较为稳定。选定触发力为50，70，90 g 进行响应面试验。

图3 触发力对最大弯折力的影响Fig.3 Effects of trigger force on the maximum bending force

2.2.4 测试距离实验结果 测试距离是设定的探头感应到触发力后以测试速度向下运行的距离。由图4可见，随测试距离的增加，数据呈现平缓变化，未见大幅波动，表明测试距离对最大弯折力无显著影响。因此不列入响应面试验。

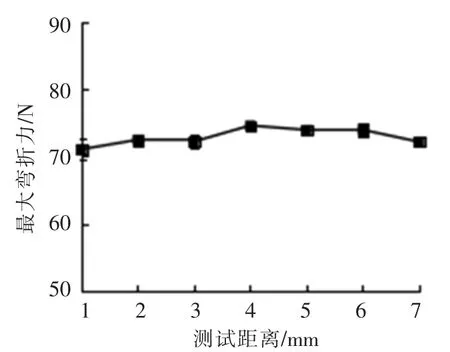
图4 测试距离对最大弯折力的影响Fig.4 Effects of distance on the maximum bending force

2.3 响应面法优化试验结果

2.3.1 响应面试验设计及结果 根据前述单因素实验结果，采用响应面分析法对测试条件进行整体优化。分别以A、B、C 表示测试前速度、测试速度、触发力，并以1，0，-1 分别代表自变量的高、中、低水平，以最大弯折力测试结果的离散度作为响应值，进行响应面分析。各因素测试水平见表2，响应面法所得结果见表3。

表2 响应面试验因素水平表Table 2 Experimental design of RSM

表3 响应面设计方案与试验结果Table 3 Design program and experimental results of RSM

（续表3）

2.3.2 模型建立及显著性方差分析 根据表3中的试验结果，利用Design Expert 10.0.4 软件得到离散度预测值对编码自变量的回归方程：Y=4.15-0.53A-0.78B-0.081C+1.18AB-1.05AC+1.12BC+2.32A2+3.90B2+1.46C2。以测试前速度、测试速度、触发力为自变量，离散度为响应值的响应面，对回归方程进行方差分析，结果见表4。

表4 响应面方差分析Table 4 Analysis of variance of RSM

由表4可以看出，整体模型极为显著 （F=28.94，P=0.0001＜0.01），失拟项不显著（F=2.28，P=0.2209＞0.05），同时方程模拟的复相关系数R2=0.9738，调整相关系数R2adj=0.9402，说明建立的模型能解释94.02%响应值的变化[22-23]，表明该模型与实际试验之间有较好的拟合度，模型成立，方法优化可靠。因素二次项A2、B2、C2对结果的影响高度极显著（P＜0.01），交互项AB、AC、BC 对结果具有显著影响，A、B、C 3 个因素对结果影响大小顺序为：测试速度（B）＞测试前速度（A）＞触发力（C）。

2.3.3 响应面曲面试验结果分析 为了直观地看出各参数之间的相互作用和最佳水平，绘制响应值对各因素所构成的曲面图和等高线图[24]。由图5～7 可见，响应面开口向上，随着各因素水平的增大，响应值先逐渐减小，至极值后又逐渐增大。最小值即是该模型的稳定点。等高线图对应响应面的增加形成一个凹点，也就是最小离散值。

由图5可见，在测试前速度（A）和测试速度（B）对响应值离散度的交互作用中，当测试速度一定时，随着测试前速度的增加，离散度先减小后增大，变化幅度较平缓。当测试前速度一定时，随着测试速度的增加，离散度呈现显著的先减小后增大趋势。因此可知，当固定触发力时，离散度随测试前速度和测试速度变化明显，两因素对离散度存在较强的交互作用。

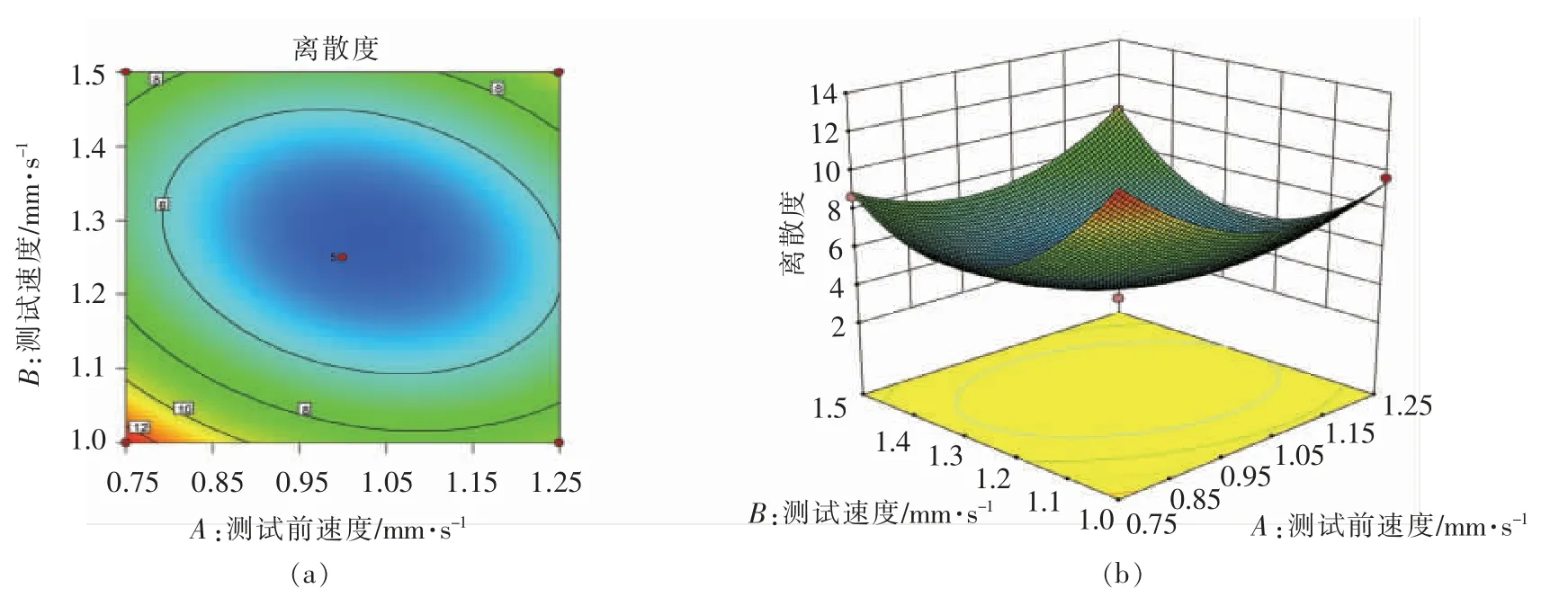
图5 测试前速度和测试速度对离散度的响应面图和等高线图Fig.5 Contour line and curved of response of pre-test speed and test speed to dispersion

由图6可见，在测试速度（B）和触发力（C）交互作用中，离散度随两因素的变化相对较平缓。当触发力一定时，随着测试速度的增加，离散度先减小后增加，变化趋势显著。当测试速度一定时，随着触发力的增大，离散度呈现较弱的先减小后增加趋势。故当固定测试前速度时，测试速度和触发力对离散度存在显著的交互作用。

图6 测试速度、触发力对离散度的响应面图和等高线图Fig.6 Contour line and curved of response of test speed and trigger force to dispersion

由图7可见，在测试前速度（A）和触发力（C）交互作用中，离散度随两因素的变化平缓。当触发力一定时，随测试前速度的增大，离散度先减小后增加。当测试前速度一定时，随着触发力的增大，离散度呈现缓慢减小，再缓慢增加的趋势。因此当固定测试速度时，测试前速度和触发力对离散度的交互作用较显著。

图7 测试前速度、触发力对离散度的响应面图和等高线图Fig.7 Contour line and curved of response of pre-test speed and trigger force to dispersion

2.3.4 最优水平验证试验 以离散度为响应值，利用Design Expert 10.0.4 软件对回归模型进行分析和验证，结果见表5。结合回归方程的三维响应面图和等高线，获得最佳测试条件：测试前速度1.026 mm/s、测试速度1.270 mm/s、触发力70.706 g。考虑到实际操作的可行性，将其修正为：测试前速度1.03 mm/s、测试速度1.27 mm/s、触发力70.7 g。在修正的测试条件下，进行10 次的平行验证试验。实测结果的离散度平均值为3.949，响应面分析的离散度理论预测值为4.090，两者之间的相对误差为3.5%。说明通过响应面法优化的测试条件参数可靠，模型准确地预测了试验结果，具有良好的应用价值。

表5 模拟的最佳条件及试验验证结果Table 5 Optimal conditions for simulation and experimental verification results

3 结论

本文对压缩干粮硬度测试的方法和条件进行了系统试验，分析了样品支撑架间距、测试前速度、测试速度、触发力、测试距离对结果离散度的影响。试验表明，当样品支撑架间距为50 mm 时，表征压缩干粮硬度的指标——折断力矩测定结果离散度最小。在此基础上，对测试前速度、测试速度、触发力、测试距离进行了单因素实验，筛选出了显著影响测定结果离散度的3 个因素及水平区间：测试前速度（0.75～1.25 mm/s）、测试速度（1.00～1.50 mm/s）、触发力（50～90 g）。利用响应面法进行了三因素三水平模拟分析，获得以上3 个因素对结果离散度影响的大小顺序为：测试速度（B）＞测试前速度（A）＞触发力（C），最佳测试条件为：测试前速度1.03 mm/s、测试速度1.27 mm/s、触发力70.7 g。在此条件下通过验证试验得到的离散度为3.949，与理论预测值相对误差为3.5%。本文建立的测试方法与条件明显提升了压缩干粮硬度测试结果的准确性和重现性。