基于改进物元可拓模型的地下水水质评价

孟洋，姜先桥，张玉辉，张立烨，范成博

1. 河北地质大学水资源与环境学院，河北石家庄050031；2. 河北省地质环境监测院，河北石家庄050021；3. 河北科技大学艺术学院，河北石家庄050018

0 引言

近些年经济社会建设与发展，地下水质量受到了不同程度影响。工业和生活用水的排放，生态环境修复能力的退化，地下水资源利用的不合理化，致使水资源污染情况日趋严峻，亟待建立科学、合理的地下水水质评价方法[1]。

目前应用于地下水水质评价的方法主要包括：综合评分法[2]、主成分分析法[3]、模糊综合评价法[4]、人工神经网络法[5]等。主成分分析法对某项单一污染源的分析更为准确，但不能全面反应水质整体状况。模糊综合评价法、人工神经网络法可对区域等大量数据进行综合评价，但其评价结果易出现均质化、分辨性差、原理和计算过程复杂等缺点。因此在水质评价中应针对于具体数据和区域水质选择相应的评价方法。相较于其他地下水水质评价方法，改进物元可拓评价模型具备处理多项指标综合评价的特点，通过系统物元变换和结构变换等方式，将不同系统的问题转化为系统问题，且能够定量表示评价结果，因此采用物元可拓模型来处理地下水水质评价问题[6]。

目前地下水水质评价中指标权重的确定方法主要有三类：主观赋权法、客观赋权法和主客观结合赋权法[7]。在综合评价过程中，权重的确定直接影响着结果的准确性、客观性、合理性。主观赋权法是根据专家的主观经验和重视程度对各项评价指标的权重进行赋值，常用的有Delphi法[8]、环比评分法[9]、层次分析法[10]等，在实际应用评价中因其过度依赖主观判断，同指标会因为专家对其主观判断的不同导致权重赋值的不同，进而影响其结果的客观性和真实性。客观赋值法是利用各项评价指标所反映的客观信息计算各指标权重，主要有主成分分析法[11]、变异系数法[12]、熵权法[13]等。指标值具有绝对的客观性，但缺少主观因素的参与可能会出现权重分配与实际重要程度相悖的情况。由于权重完全由样本数据所决定，只有当实测数据具有普遍性和典型性时，才能确保得到权重的合理性。主客观结合赋权法是主观赋权法和客观赋权法相结合的一种方法，既保留了主观赋权法的主观判断，也反映了实际数据的客观分析。本文采用层次分析法和主成分分析法相结合的赋权方法。

本文利用三个维度构建评价体系：感官指标、一般化学指标和毒理学指标。改进物元可拓评价模型应用的关键是评价指标权重的确定，本文采用层次分析法和主成分分析法综合确定权重，以期得到更为科学、准确、合理的评价结果。将所构建基于改进物元可拓的模型对河北省冀东某县及周边区域地下水水质进行评价，并与综合评分法、单因子评价法、模糊综合评价法进行对比，验证所提出水质模型的准确性、科学性。

1 确定地下水水质评价指标

本文从感官、一般化学指标和毒理学三个维度构建的水质评价体系中，感官指标包括2个二级指标，一般化学包括7个二级指标，毒理学指标包括6个二级指标，即由3个一级指标、15个二级指标共同构成地下水水质综合评价体系。评价体系结构示意图如图1所示。

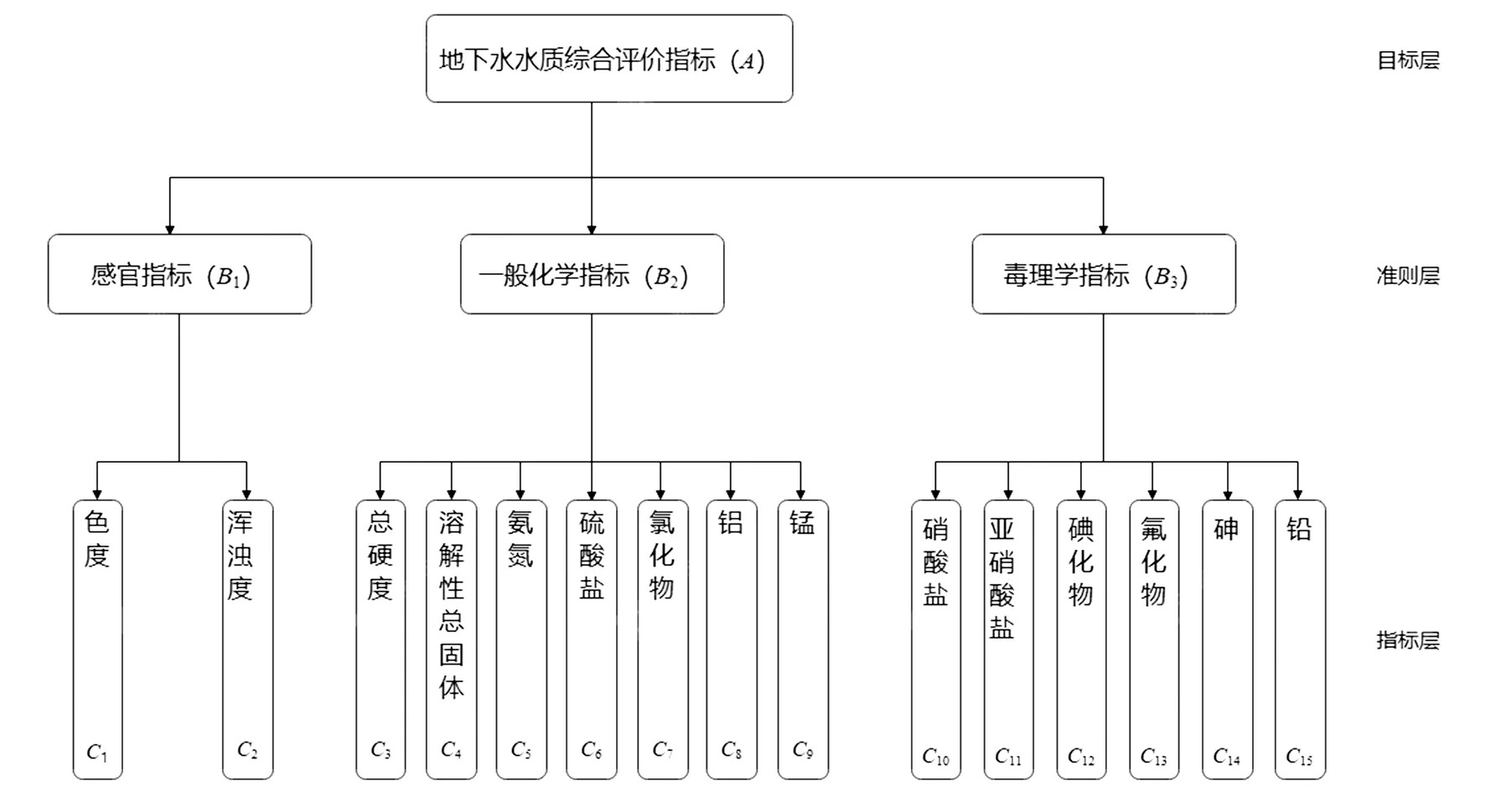
图1 地下水水质综合评价结构图Fig.1 Structure chart of groundwater quality comprehensive evaluation

地下水评价标准执行《地下水质量标准》（ GB /T 14848-2017）[14]，将水分为五类，常规层各项指标Ⅰ—Ⅴ分类标准如表1所示。

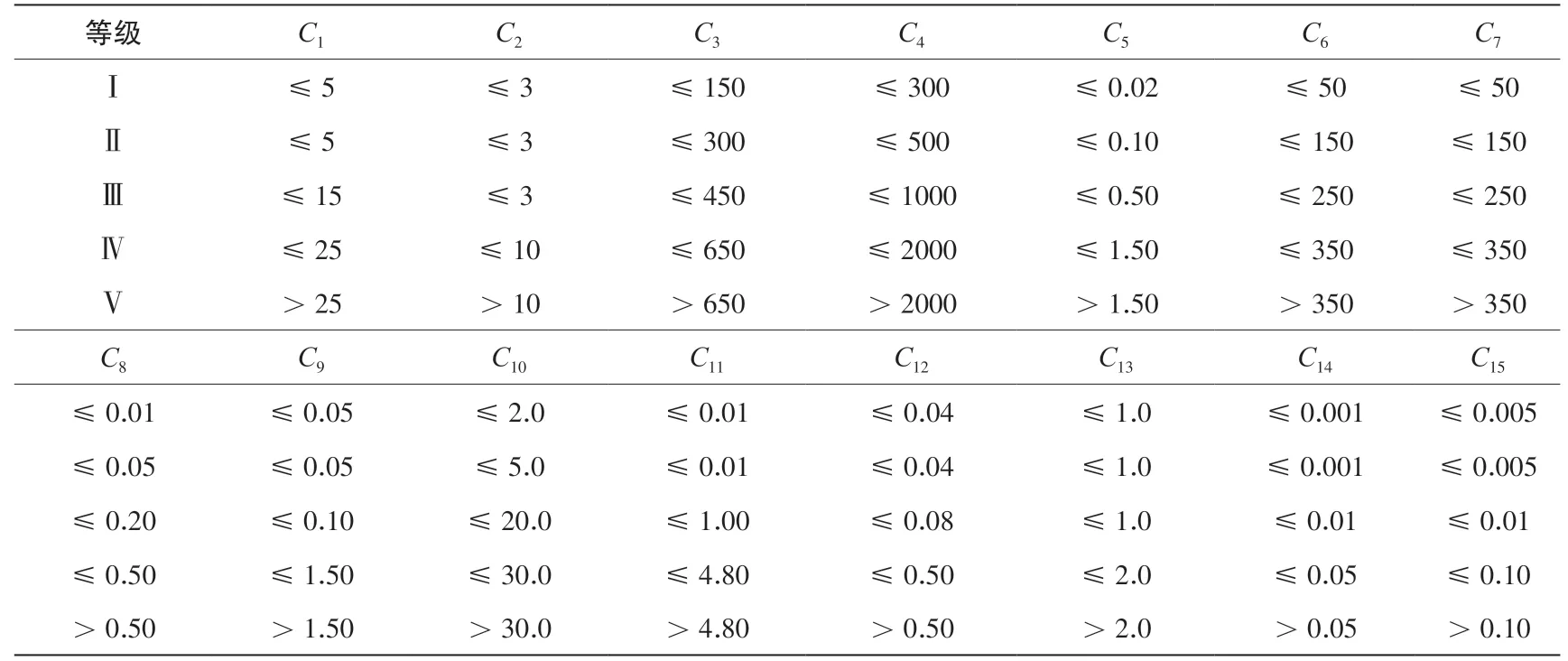
表1 地下水水质评价标准Table.1 Evaluation standard of groundwater quality

2 计算指标权重

在多指标综合评价过程中，各指标权重的确定十分关键，评价结果的准确与否能充分验证权重的合理性、客观性。指标权重的确定方法有许多，但每种方法都存在不同的利弊，若采用单一的理论方法来确定权重必然会影响评价结果的准确性，因此本文采用两种方法相结合求得综合权重，综合两种方法的优势，确保评价结果科学性和准确性。

2.1 层次分析法

层次分析法（Analytic Hierarchy Process，AHP）是一种将定量和定性相结合，具有层次化和系统化的分析方法[15]。以研究者的研究经验和主观判断为主，根据构建的层次结构模型，采用专家咨询法通过对评价指标中各因素重要程度两两定量比较，得到层次间模糊判断矩阵，即目标层与准则层模糊判断矩阵。计算特征值λmax和对应的特征向量W，在经归一化处理代表的是某一层的全部因素关于上一层的某一因素的权值分配。由于研究者主观认识的随机性，且易受专家主观判断的影响，需要进行一致性检验，以保证构造的判断矩阵的科学性。只有当一致性比例IR< 0.1 时，表明判断矩阵一致性较好，此时不需要对其进行调整。一致性指标和随机一致性指标分别通过公式（1）和（2）计算：

式中：IC为判断矩阵一致性指标；IA为判断矩阵平均随机一致性指标；IR为判断矩阵随机一致性指标；n为判断矩阵阶数。

当矩阵阶数不同时，其一致性指标取值如表3所示。

表3 矩阵阶数n对应的平均随机一致性指标IA的取值Table.3 The value of average random consistency index IA corresponding to matrix order n

虽然准则层对于指标层都通过一致性检验，但3个准则层经叠加后的一致性还未能明确，所以需要通过公式（3）进行叠加后的一致性检验，若也能满足IR<0.1，说明各指标整体具有较好的一致性。

式中：bi为第i个准则层权重；IC为第i个准则层一致性指标；（IA）i为第i个准则层平均随机一致性指标。

表2 指标重要程度Table.2 Importance of indicators

2.2 主成分分析法

主成分分析法是通过统计分析将多个变量组合筛选，以少数变量表达同等信息量的方法[16]，这较少的几个综合指标要尽可能多地包含原变量所表达的信息，且这少数几个综合指标包含的信息不重叠即互不相关，而这些综合指标就是主成分。主成分分析法确定权重的具体步骤如下：

（1）根据收集到的n个水质样本和m个评价指标，构建原始数据矩阵

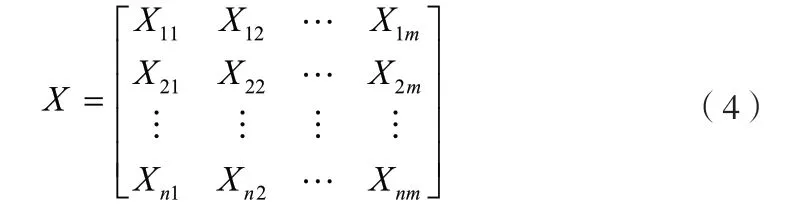
（2）实际问题中，为避免各指标间量纲不同，常利用下式将上述数据进行归一化处理

式中：βi为第i个主成份（k=1，2，…，p）的贡献率。

求前k个的累积贡献率，实际中通常要求累积贡献率达到85%以上，即ηk≥85% 。

式中：ηk为前p个主成分的累积贡献率。

（5）各指标对总体方差的贡献矩阵F，通过主成分总体方差贡献矩阵A与各指标主成分贡献矩阵C相乘，求得贡献矩阵F，矩阵中fi（i=1，2，…，p）各元素为对应指标权重值。

2.3 综合权重

计算最终权重，本文应用公式（13）分别将层次分析法与主成分分析法计算得到的权重进行耦合计算，得到综合权重。

式中：ωi为层次分析法计算得到的指标权重；hi为主成分分析法计算得到的指标权重。

3 改进的物元可拓模型

物元理论是介于系统科学、思维科学、数学交叉的边缘学科，物元分析是研究物元及其变化并用以解决矛盾问题的规律和方法[17]。物元可拓模型能够将评价体系中多指标问题整合转化为单指标问题，且模型评价结果能定量化体现。在应用物元可拓评价模型时，可消除地下水水质界限的模糊性和水质变化的随机性[18]。构建改进物元可拓模型，一般需要6步：构建待评物元，确定经典域、节域；对经典域、节域和待评物元进行规格化处理；计算待评物元关于经典域物元量值的距离；构造关联函数；计算确定关联度；确定评价等级。本文对物元可拓评价模型进行改进，避免出现评价指标实际值超过节域范围，确保构造的关联函数能满足计算要求。改进思路是对构建的物元可拓评价模型经典域和待评物元矩阵进行规格化处理，物元可拓评价模型改进步骤如下：

（1）规格化处理经典域和待评物元矩阵。将经典域物元矩阵RN中的各指标的量值两端和待评物元矩阵R0中的量值都除以节域中各指标取值范围的最大值。

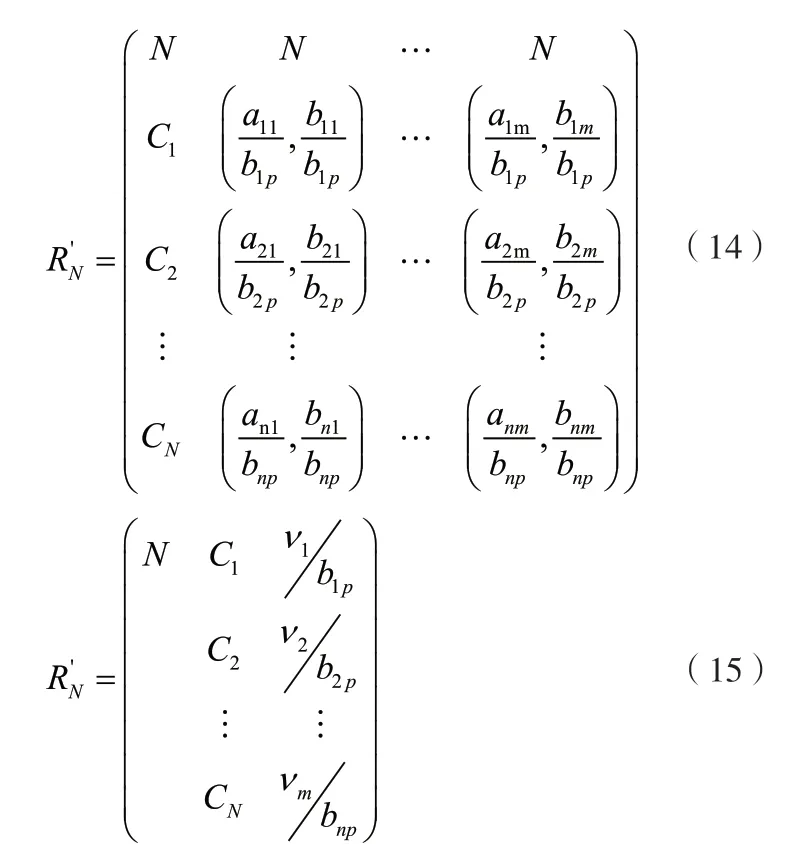
式中：N为待评对象；Ci（i=1，2，…，n）为待评对象N的第i个指标，Nj（j=1，2，…，m）表示评价对象所划分的第j个评价等级; （aij，bij）为第i个指标关于评价等级j的数值范围（i=1，2，…，n，j=1，2，…，m）；bip（i=1，2，…，n）为第i个指标取值范围的最大值；ni（i=1，2，…，n）为待评对象第i个指标的值。

（2）计算规格化后的待评物R'0元关于新的经典域R'N物元量值范围的距离Dij。

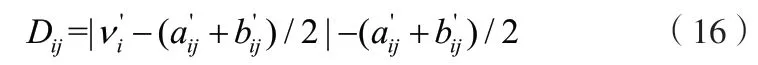
式中：v'i、a'ij、b'ij分别为规格化处理后的vi、aij、bij。

（3）将距离计算Dij引入综合关联度函数中，计算确定评价等级。

式中：gi为第i项指标的最终综合权重，结果Kj中最大值Kjmax所属的等级即为最终评价等级。

4 案例分析

将物元可拓评价模型应用到河北省冀东某县及周边区域地下水水质评价中，采用多角度、多方法对研究区地下水水质进行综合全面的分析评价。以河北省冀东某县及周边区域13眼监测井为研究对象，地下水水样的采集、保存、检测均严格按照《地下水环境监测技术规范》（ HJ/T164-2004）执行。研究区域水样采集，取样点控制面积达1 482.6 km2。地下水水质监测井密度为7.6眼，满足《SL183-2005地下水监测规范》地下水水质监测井密度 1.0～1.6 眼/103km2的要求。选取15项指标作为参评指标，指标分类与等级划分标准主要依据《地下水质量标准》（ GB /T 14848-2017）[14]进行确定。研究区各监测井地下水水质各项评价指标实测值如表4所示。

表4 研究区各监测井地下水水质各项评价指标实测值Table.4 The measured value of groundwater quality evaluation indexes of each monitoring well in the research area

4.1 综合权重的确定

计算研究区地下水各项指标综合权重，从层次上分三步，先用层次分析法确定权重，再用熵权法确定权重，最终计算求得综合权重。

（1）应用层次分析法的基本原理，在结合专家、研究者和相关文献的基础上，构造目标层A对应的准则层B的判断矩阵P。

由计算可得矩阵P一致性指标IC=0.004 5，平均一致性指标IR=0.58，经一致性检验公式计算可知一致性比例RC=0.008＜0.1。故矩阵满足一致性要求，即所求的最大特征值λmax及所对应的特征向量Wp为准则层指标B1、B2、B3对目标层A的权重系数，Wp=[0.297，0.164，0.539]。同理可得指标层C各指标对准则层B的权重系数：W1=[0.667 0.333 ]；W2=[0.1230.141 0.064 0.031 0.049 0.244 0.348 ]；W3=[0.064 0.042 0.101 0.160 0.381 0.252 ]。

（2）应用主成分分析法求权重，通过spss软件进行归一化处理、求出指标数据的相关系数矩阵、求得与之对应的特征值和特征向量，前5个成分的累积贡献率高达91.62%＞85%，因此主成分（硫酸根、总硬度、锰、溶解性总固体、浑浊度）基本可以反应全部指标的信息。经软件计算得出指标层C指标对准则层B的权重系数：W1=[0.067 0.068]；W2=[0.068 0.0740.053 0.067 0.068 0.059 0.071]；W3=[0.074 0.064 0.077 0.058 0.057 0.075]。

（3）计算综合权重，依据公式对层次分析法和主成分分析法求出的权重进行耦合计算，计算各层指标相对应的权重如表6所示。

表5 相关矩阵的特征值及其累积贡献率Table.5 Eigenvalues and cumulative contribution rate of correlation matrix

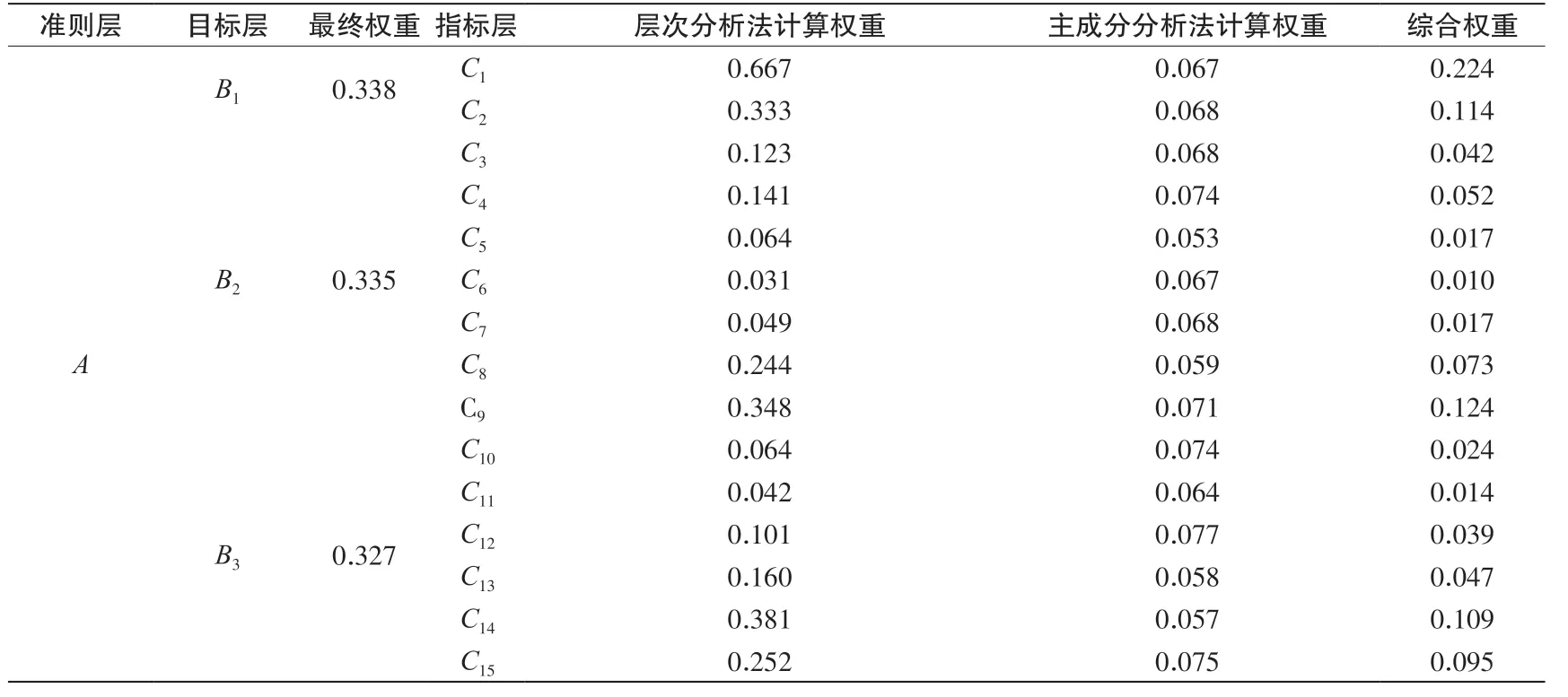
表6 各指标、目标层综合权重Table.6 Comprehensive weight of each index and target layer

对以上数据进行分析可知，感官指标、一般化学指标和毒理学指标重要程度相差不大，通过分析主成分分析法得出的权重可以看出，从客观数据出发求得的权重更为平均，说明研究区内某项指标的水质未出现极值现象。就整个评价体系中15项评价指标的权重可以分析得出，评价指标中色度、锰、浑浊度、砷、铅的权重之和为0.665，这几项指标和其他指标相比重要程度较大。

4.2 构造经典域、节域和待评物元矩阵

由于《地下水质量标准》（ GB/T 14848-2017）[14]中Ⅴ类水上限值没有明确，且参评监测点水质样本中未发现严重超标因子，故本文评价模型中采用Ⅰ-Ⅳ类水评价标准，这既简化了计算过程，又能达到评价要求。通过指标赋值构建待评物元RO。

地下水水质等级N，地下水水质评价指标C。根据表1中数据构造Ⅰ、Ⅱ、Ⅲ、Ⅳ级分级标准的经典域矩阵，并按公式规格化处理经典域矩阵R0，得到新的经典域矩阵。

按照公式规格化后新待评物元R'0。

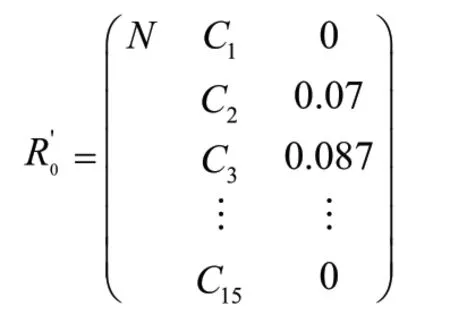
根据公式计算出测点1中15个地下水水质评价指标关于Ⅰ、Ⅱ、Ⅲ、Ⅳ级评价等级的距离，结果为：

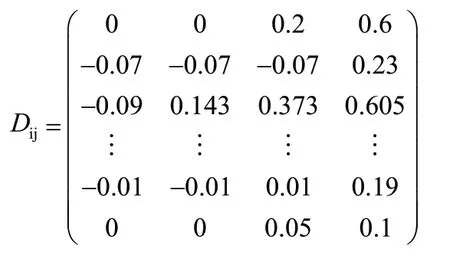
根据公式计算综合关联度Kj，得到K1=0.8455，K2=0.828 6，K3=0.747 3，K4=0.553 0。经计算可得 （max）Kj=0.845 5，可知测点Y1的地下水水质等级为Ⅰ级。

其他点位数据，同理按照Y1点地下水水质评价过程计算求得，通过对计算求得的关联度，并按照模型评价方法确定其13个点的水质等级。为了对比验证，综合权重和改进物元可拓评价模型对地下水水质评价结果的合理性和准确性，运用《地下水质量标准》（ GB /T 14848-2017）[14]中采用的综合评分法和单因子评价法，以及综合模糊评价法（此评价方法权重取值同样采用本文权重计算值）对13个监测点的地下水水质等级进行综合评价，评价结果如表7所示，并将4个不同方法评价出的结果进行对比，如图2所示。

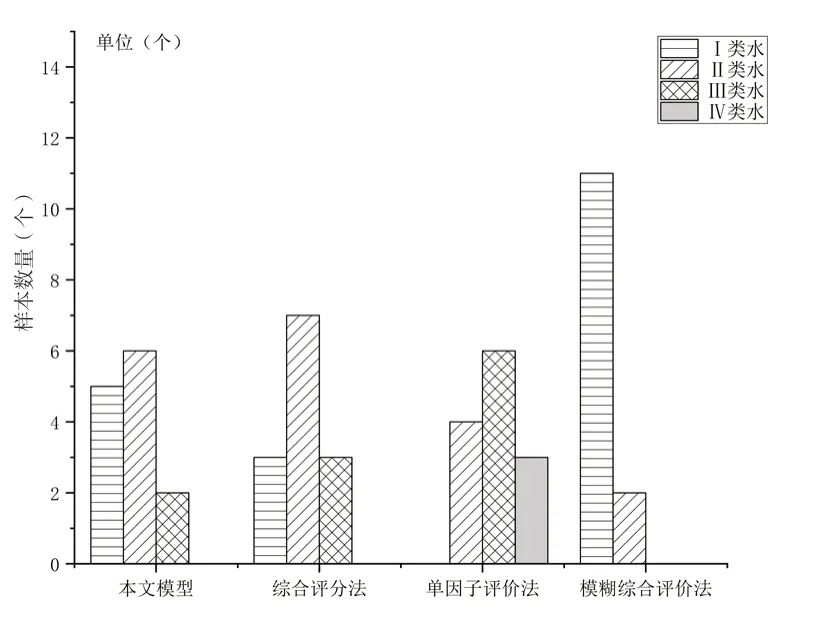
图2 各评价方法结果对比图Fig.2 Comparison of results of each evaluation method

表7 各监测点关联度计算结果及水质评价结果对比Table.7 Comparison of correlation calculation results and water quality evaluation results of each monitoring point

4.3 评价结果分析

由表7所示对13个监测点，运用4种评价方法所得的评价结果进行分析。从本文模型评价结果来看，此地区地下水水质较好，多为Ⅰ、Ⅱ类地下水，占比依次是38.5%、46.1%，累计占比84.6%，仅点Y10、Y11点为Ⅲ类水。比较分析综合评分法和单因子评价法，运用这两种方法普遍得出的评价结果偏差，其中单因子评价法尤为严重，普遍比综合评分法低一个等级。模糊综合评价法得出的水质等级偏高，一类水占比高达84.6%。本文评价模型介于综合评分法、单因子评价法和综合模糊评价法之间。

对比本文评价模型和综合评价法水质评价结果，评价结果相同和结果相差一个等级占比为61.5%和23.1%，累计占比达84.6%，监测点Y4评价结果差异较大。分析评价结果相差较大的原因：本文评价模型的权重是综合考虑各项指标在评价体系中所占的重要程度，后给予不同指标不同权重，而综合评分法在评价过程中各项指标的权重值是相同的。因此在评价结果上存在较大差异。

对本文模型与单因子评价法水质评价结果进行对比分析可知，整体来看单因子评价法得到的结果相对较差。单因子评价结果按单项指标最差的来确定最终水质等级，这一方法评出的水质难免与实际水质存在差别。以某项指标的最差等级来表征整体水质情况，可以直观地反映出主要污染因子。这一方法更为直接，且评价结果更加严格。反观本文评价模型，更能从多指标体系化层面反映水质等级。

分析模糊综合评价法得出的水质评价结果，发现其结果要明显优于其他评价方法。模糊综合评价法一类水占比明显高于本文模型。分析造成此评价结果的原因，是由于相对隶属度权系数往往偏小，评价结果易出现均质化、分辨性差。因此若利用模糊综合评价法去评价地下水水质等级时，可能出现评价水质等级要比实际水质等级高的情况。

综合以上分析，基于综合权重和改进物元可拓评价模型，在地下水水质评价中的应用，不仅可以充分考虑到各项评价指标的权重的差异性，且能避免水质等级的模糊性和不确定性，合理准确地评价出水质等级。其评价结果要优于综合评分法、单因子评价法和模糊综合评价法，评价结果更加合理，表明本模型适用于此研究区，能够较为科学地评价此地区地下水水质等级。

5 结论

（1）从感官指标、一般化学指标和毒理学指标三方面构建地下水水质评价体系，并运用层次分析法和主成分分析法分别计算各指标权重，最终得出综合权重，结果表明色度、锰、浑浊度、砷、铅权重值相对较高，在地下水水质评价过程中更能影响评价结果，应着重关注。

（2）从样本数据分析可知，监测点Y4评价结果差异性较大，点Y4铅含量达到Ⅳ类水标准，含量0.010 6 mg/L，另外此点有3项指标达到Ⅲ类水标准，其余11项指标均满足Ⅱ类水及以上标准。虽然未达到《生活饮用水卫生标准》（GB5749-2006）[19]规定的饮用水水中铅的界限值0.01 mg/L，但仍可适用于农业和部分工业用水。

（3）模型中将层次分析法和主成分分析法所求权重进行耦合计算，有效地将两种方法的优势结合，提高了权重的合理性。改进物元可拓模型，消除了各评价指标间不相容的问题，还考虑了水质等级的不确定性、模糊性。其评价结果与综合评分法、单因子评价法和模糊综合评价法对比，表明本文模型是可行的，能更科学、合理、准确地评价本研究区的地下水水质。

（4）依据《地下水质量标准》（ GB /T 14848-2017）[14]，运用本文模型对河北省冀东某县及周边区域13个监测点的地下水水质进行综合评价。其结果表明，该地区地下水水质等级多为Ⅰ类水和Ⅱ类水，水质较好，可指导该区域水资源利用规划，为水资源合理利用提供依据。对于水质较差的地下水，应进一步查明水质超标指标、超标原因，采取相应的防治措施，防止污染进一步恶化，为地下水水质改善提供基础条件，保证地下水系统的健康良好发展。