基于十字形扫描雷达的3D料面建模方法
2021-09-09刘怀广陈先中
李 佳, 张 亮, 刘怀广*, 陈先中
(1.武汉科技大学冶金装备及其控制教育部重点实验室, 武汉 430081; 2.北京科技大学自动化学院, 北京 100083)
高炉料面形状描述模型有利于研究高炉内部料面变化情况,是实现炼铁过程精细化和自动化的基础。实际生产中,料面形状描述模型的精确性和适配性是保证冶炼过程正常运行的关键因素。因此,关于提高料面描述模型精度的研究对高炉炼铁具有重要意义[1]。
近年来,中外学者对高炉料面形状模型进行诸多研究,根据雷达检测方式可分为2D料线描述模型和3D料面描述模型[2]。2D料线描述模型数据来源于稀疏离散位置高度值[3],对数据进行插值或拟合获得描述料面径向料线形状的曲线。关心等[4]祝乔等[5]基于六点雷达数据,采用三次多项式曲线获得2D径向料形描述模型。魏纪东等[6]、关心[7]设计机械摆动扫描雷达对高炉料面径向高度进行检测,通过三次样条函数插值形式进行料线形状描述。上述研究可以获取径向2D料线拟合模型,但在在非对称料面状态下,单条拟合料线并不能代表整个料面,料线拟合模型误差较大。
张海刚[8]基于相控阵雷达对各个位置料面高度的检测,结合算法[9]合成3D料面描述模型。3D料面描述模型可以直观获取料面三维信息,但过度依赖全料面数据点的检测[10]。关于离散雷达数据点的3D料面描述模型研究较少。
基于上述料面建模研究可知,雷达数据检测方案和料面描述方式的改进尤为重要。现从如下几个方面实现高炉料面建模:基于雷达数据点提取原则提出十字形数据点检测方案;利用分段特征料线拟合方法得到4条料线方程;基于环形料面近似相同特征提出任意位置高度值计算方法;采用MATLAB二维插值法进行高炉3D料面插值拟合;最后通过数值仿真对研究方法进行验证。
1 雷达数据点的提取原则
为了更加清晰地表达清楚高炉内部的实际炉况,雷达监测数据点提取至关重要。本节将结合高炉料面特征和料线描述模型关键点提出满足插值要求的数据提取原则。
1.1 高炉料面特征
高炉料面是由矿石及焦炭颗粒堆积成的面状体,料面形状是由布料方式决定。多环布料在实际生产中应用最多,对多环布料工艺[11]进行分析,得出料面形状有如下特点:
(1)圆周对称性。为保证炉料充分反应,工艺上要求料面形状标准圆周对称。
(2)料面形状组成[12]:漏斗形区域、平台区域及边缘区域。曲线和直线组成的漏斗区域;曲线组成的平台区域;直线组成的边缘区域。
(3)局部偏心性。高炉冶炼过程会出现偏料、管道和局部风口不活跃等不良炉况,造成料面在同一圆周上不均匀地下降,因此料面具有一定局部偏心性。
1.2 料面关键点定义
利用检测点信息重构料面整体形状,常用的建模思路是依据雷达获取有限个数据测量点,采用插值拟合获得料面径向料线。此种方法有较高的计算效率但插值效果与实际情况偏差较大。在高炉径向方向上进行分段插值拟合计算,料面实际情况如图1所示。结合实际料面情况特征建模。如图2所示,A点表示V形的深度,B点和C点之间的距离为平台的宽度,A、B、C点是描述料面方程的主要参数,为作为料面关键点,同时获取的离散检测数据点越多,料线插值精度越高。

图2 分段拟合料线形状图
1.3 雷达数据点提取原则
现结合高炉料面特征和高炉料面特征描述模型要求,提出改善高料面建模精度的数据点提取原则。
(1)等差分布原则:数据点距离炉心的距离呈等差分布,且距离最小的数据点接近炉心位置,距离最大的数据点接近炉墙位置。
(2)圆周等布均匀原则:根据雷达传感器布设评价函数[13],数据点应该是圆周均匀分布。
(3)关键点覆盖原则:根据料面形状特征,需要检测点覆盖料面关键点。如漏斗型料面的炉心点A及曲线与直线连接点;平台区域的转接点BC的宽度。
(4)数据点多重覆盖原则:料面可能出现一定的非旋转对称性,相同半径数据点采集多重覆盖将提高料面建模精度。
2 检测数据提取及处理方式
2.1 十字形雷达数据提取方案
为了提高料面建模精度,本文结合高炉内部环境和雷达数据点提取原则提出十字形数据点检测方案,如图3、图4所示。其中α为溜槽倾斜角,雷达数据点的分布是以炉心为中心对称的十字形,十字形数据点有4条径向料线组成,每条径向数据点呈等差分布符合原则(1)和(3);4条径向料线整体圆周分布满足原则(2)和(4)。料面扫描单元以通过机械式扫描雷达进行特殊轨迹扫描获取呈中心对称的十字形分布雷达检测点。

图3 十字形数据测量方案示意图

图4 十字形数据点分布图
2.2 十字形雷达数据处理方式
在进行2D料线描述和3D料面特征描述时,传统方法假设料面呈完全中心对称,与实际料面情况相差较大。为提高非对称料面建模的精度,对十字形雷达数据点进行处理,匹配上述两种不同料面描述模型。
2.2.1 2D料线建模时十字形数据的处理
2D料线作为指导布料操作重要指标,以一条径向料线代表整个料面。为使2D料线更逼近真实料面特征,对十字形数据检测点进行加权平均计算,采用空间平均和区域平均对每组数据进行处理。如图5所示,Hx+n、Hy+n、Hy-n、Hy-n表示在半径r=n时对应的十字形雷达数据检测点高度信息,则处理后的数据点Hnr计算公式为

图5 十字形数据点处理示意图

(1)
Hnr更加能反映半径r=n时料面高度信息,因此作为2D料线拟合的数据点,更加符合料面特征。此种方法将减少特异点对料线重构的影响,适用于非对称料面的2D料线重构。
2.2.2 3D料面建模时十字形数据的处理
基于MATLAB二维插值实现离散数据可视化,完成料线到料面的融合,也是指导高炉生产的重要指标。十字形数据点测量点法只能得到径向料线的各个点的高度信息,不能全面反映整个料面各处的高度信息。结合十字形数据和高炉料面特征,提出高炉某点高度计算方法。
通过料面空间插值计算方法来计算整个料面某点的高度信息。如图4所示建立空间坐标系,计算空间中某点高度信息的工作平面中进行计算,由于高炉布料采用环形周期布料,通常与原点距离相等点的高度信息相对比较接近,所以本文采用如下算法根据十字形数据点的测量值确定料面中每个点的高度信息,以图4中m处的高度zm为例计算说明。

将两坐标轴的距离作为权重,求取zm,如式(2)所示:
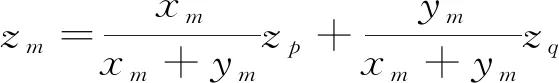
(2)
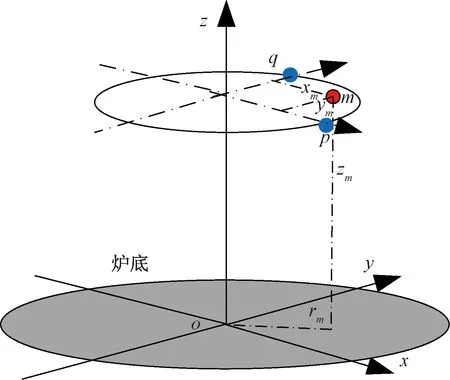
图6 高炉空间某点示意图
依据上述方法对十字形数据进行处理,计算出整个十字数据平面中每个点的高度信息,结合MATLAB插值数据要求,得到高炉料面进行二维插值的数据。
3 十字形数据单条2D料线描述模型
高炉2D料线的特征参数反映真实生产状况,因此描述模型需更加符合料面实际情况。传统的料线特征刻画模型过于简单, 难以应用于复杂的真实生产现场。为了更真实地反映高炉生产情况,本节基于料面特征和十字形数据点的提出新的2D料线描述模型。
3.1 2D料线定义方式
结合现场专家经验,根据典型料面的径向料线特征,最终确定了单条径向料线的4个区域的特征参数,如图7所示。图中半径料线分为4个区域:漏斗区、直线区1、平台区及直线区2,其中a、b、c、d分别为几个区域的分界线。以圆弧描述漏斗区的料线特征,提取圆弧半径、圆心角炉心处的料面高度特征;以一段倾斜直线描述直线区1的料线特征,提取直线倾角及漏斗深度特征;以圆弧描述平台区料线特征,提取平台区圆弧半径、圆心角及水平宽度特征;以直线描述直线区2的料线特征。图7中具体的料线参数定义:炉心处料面高度h1,漏斗的深度h2,漏斗圆弧半径为r1和r2,圆弧角α1和α2,直线区1线倾斜角β1,平台区宽度l1,直线区2的倾斜角β2。

图7 2D料线特征定义示意图
3.2 2D料线拟合方程
为了能够准确有效地提取料线特征参数, 采用两段曲线和两段直线的描述方法进行料线的重构。几何图形的都有科学的描述,圆心角和半径是确定圆弧轮廓的关键因素。倾斜角是确定直线的关键性因素。将雷达检测点数据设定为(xi,yi)(i=1,2,3,…,a,b,c,d,e,f)。基于雷达数据点离散点定义对本研究的料线特征进行确定,特征参数的具体计算过程如下。
炉心料面的高度h1为
h1=ya
(3)
漏斗的深度h2、半径r1及圆心角α为
h2=yc-ya
(4)

(5)

(6)
直线区的直线倾角β1及β2为

(7)

(8)
平台区的宽度l1及半径r2为
l1=|xd-xc|
(9)

(10)
根据径向料线定义坐标系,曲线拟合方程为

(11)
十字形扫描雷达获得四条沿径向分布的离散数据点,通过上述料拟合方法可以获得4条不同的2D料线,为3D料面重建做准备。
4 十字形数据3D料面描述模型
为了更加精准的实现高炉雷达监测数据的可视化,拟在2D料面的基础上采用2D料线拟合方程和高炉料面空间高度计算方法实现线面融合,重构高炉3D料面。MATLAB二维插值法可以实现数据可视化,本文结合高炉料面特征和插值原理对所测量的料面进行网格划分,插值矩形的分布如图8所示。利用interp2函数实现二维插值,具体插值原理如下。

图8 高炉料面插值栅格数据点示意图
由4条径向料线获得m×n个雷达数据节点:
(xi,yi,zij),i=1,2,…,m;j=1,2,…,n。
其中xi、yi互不相同,其区间范围[Lx,Ux],[Ly,Ux]。不妨设:

(12)
构造一个二元函数z=f(x,y)通过全部的已知节点,即
f(xi,yi)=zij,i=1,2,…,m;j=1,2,…,n
(13)
5 模型的实验验证
为了验证所提出的方法的有效性,基于某高炉实测数据利用本文研究中的计算方法进行数值拟合仿真:料面呈非完全对称状态下的2D料线拟合效果;离散数据点3D料面拟合效果。
5.1 高炉2D料线数值仿真
通过现场提取的某高炉实测数据,利用本文计算方法进行料面数值仿真,与六点阵列雷达和沿高炉料面径向扫描雷达的2D料线拟方法进行对比,对比效果如图9所示。
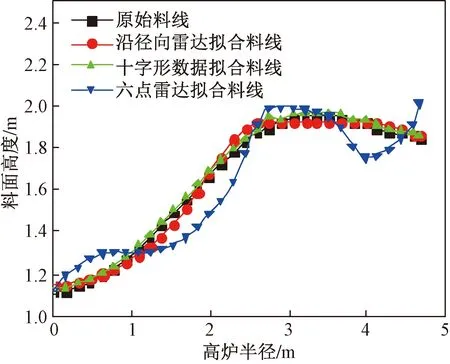
图9 2D料线拟合对比效果图
为比较三种料线拟合方式的精度,计算均方误差公式如(14)所示:

(14)

表1 MSE计算结果
由表1可以看出:十字形数据和沿径向数据料线拟合方法可以获得2D料线;十字形数据拟合料线的拟合均方误差0.051 5,更加符合料面实际堆积特征,相较于其他两种方法精度更高。
5.2 高炉3D料面仿真
结合3D建模方法对某高炉进行3D料面重构:对本次测量料面的数据而言,a和c是-4.5 m,b和d是4.5 m。为构建高炉料面插值函数,对所测区域进行网格划分,获取十字形数据点构造4条料线,结合空间高度信息计算方法得到满足条件的插值数据点,根据雷达覆盖炉内料面的有效面积,计算出所需雷达数据点在半径方向上是6个,因此本节中仿真插值数据为11×11矩阵,即插值数据点为121。利用interp2函数进行插值,二维插值函数的调用格式为
z=interp2(xi,yi,zi,x,y,’spline′)
(15)
式(15)中:x、y、z为二维插值函数使反映高炉高度的数据点;’spline′为三次样条函数插值。
料面拟合结果如图10所示,本文中提出的基于MATLAB二维插值方法可以实现离散数据点高炉料面重构,并且从料面高度分布图11可以看出,料面模型符合实际生产的环形对称。

图10 十字形数据料面拟合模型
6 结论
现提出一种结合十字形数据和MATLAB二维插值进行料面重构描述模型的方法,用于离散数据点的3D料面重构。得到以下结论。
(1)利用数据点进行料线2D拟合时,十字形数据点减少料面特异点对料线拟合的影响,提高了2D料线拟合精度。
(2)基于十字形数据点和MATLAB二维插值方法进行高炉料面,实现了高炉雷达离散数据点的3D可视化,为提取高炉料面分布信息,获取料面变化趋势提供了一种更加直观全新的方案。
(3)基于十字形数据点的高炉料面空间高度计算方法符合料面堆积特征,为高炉任意位置空间信息的计算提供一种思路。
