基于置信语言直觉模糊GMSM的决策

王红娟

(内江师范学院，四川 内江 641100)

1 背景

决策方法近年来受到越来越多学者的关注[1,2]，它是通过专家对方案的信息用模糊数进行评价进而从有限方案里选出最优方案。Atanassov[3]介绍了直觉模糊数，用隶属度和非隶属度分别表示专家的满意和不满意。Deschrijver等[4]给出了直觉模糊数的概念。直觉模糊数的隶属度和非隶属度都是精确值，有一些复杂的情形，专家不能够通过精确值给出隶属度和非隶属度。为了解决上述问题，Zadeh[5～7]提出了语言变量的概念。Chen等[8]提出了语言直觉模糊数根据语言变量和直觉模糊数，语言直觉模糊数的隶属度和非隶属度都是语言变量。可以得到语言直觉模糊数要更容易表示模糊信息比直觉模糊数，因为隶属度和非隶属度都是语言变量不是精确值。语言直觉模糊数在决策方法里得到很多应用[9,10]。

在决策方法里，第二个步骤是如何将方案的不同属性评价信息聚合，选出最优方案。有两种方法，其一是传统评价方法 ，其二是信息聚合算子。传统方法只能得到方案的排序，信息聚合算子不仅能够给出排序还能得到各个方案的综合评价，因此信息聚合算子要比传统的方法更能解决决策问题。因此聚合算子特别有用和重要。在决策问题中，属性之间存在相互关联性在聚合信息时需要考虑属性之间的关联性，例如在购买产品时，质量和价格息息相关。下面介绍一些聚合算子，Bonferroni[11]介绍了Bonferroni mean (BM)算子，这个算子考虑任意两个属性之间的相互关联。Maclaurin[12]提出了Maclaurin symmetric mean (MSM)算子，这个算子考虑属性之间的相互关联，由于它的该种性质，MSM算子在许多决策问题中使用[13～16]。MSM算子要比BM算子更实用在决策问题中，因为BM只考虑任意两个属性之间的关联，MSM可以考虑任意多个属性之间的相互关联性。Wang等[17]提出了GeneralizedMSM (GMSM)算子，GMSM是MSM、BM等的推广，给GMSM的参数设置不同的值，GMSM算子转化为其他算子[17]，因此，GMSM要比其它算子更一般化。

在决策问题中，专家不一定对方案的属性信息完全熟悉(置信水平)。通过结合专家的置信水平和专家的评价信息在q阶orthopair模糊数环境中，Bhagawati等[18]给出了一些置信q阶orthopair模糊聚合算子，置信q阶orthopair模糊加权平均 (CFWAq)、置信q阶orthopair模糊有序加权平均 (CFOWAq)、置信q阶orthopair模糊加权几何 (CFWGq)、和置信q阶orthopair模糊有序加权几何 (CFOWGq)。在已有的语言直觉模糊环境中并没有考虑专家对方案的属性信息的熟悉程度，即置信水平。因此，本文结合置信水平和语言直觉模糊数，给出置信语言直觉模糊GMSM (CLIFGMSM)和置信语言直觉模糊加权GMSM (CLIFWGMSM)。GMSM算子要比MSM算子更一般化，在决策问题中更加切实可行。

本文其他几部分：第二部分介绍语言直觉模糊数和GMSM算子概念，语言直觉模糊数比较大小的方法；第三部分提出置信语言直觉模糊GMSM和置信语言直觉模糊加权GMSM及算子的性质；第四部分介绍了一种新的决策方法通过实例和Liu等[19]介绍的方法比较说明所介绍方法的切实可行；第五部分是结语。

2 基础知识

语言直觉模糊数和GMSM算子。

定义1[8]假设S={Sp|p∈[0,r]}是连续语言集。对于Sp,Sq∈S，如果p+q≤r，则称s=(Sp,Sq)为语言直觉模糊数。用Y[0,r]表示所有语言直觉模糊数的集合。

设si=(Spi,Sqi)(i=1,2)，则:

(1)

(2)

(3)

(4)

语言直觉模糊数之间的比较：

定义2[20]设si=(Spi,Sqi)(i=1,2)，则s1与s2的广义语言直觉模糊距离为:

d(s1,s2)=

(5)

式(5)中,πi=r-pi-qi(i=1,2),γ≥1。

定义3[20]设s=(Sp,Sq)，s′=(Sr,S0)是正理想点，则s的排序指标为：

(6)

从式(6)可以得到，从s到s′的距离越小，方案越接近于理想点。因此，R(s)的值越小，选择s越好。

定义4[17]算子GMSM定义为：

GMSM(t,κ1,…,κt)(a1,…,al)=

(7)

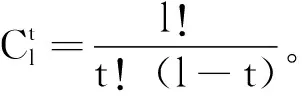
3 置信语言直接模糊GMSM和置信语言直接模糊加权GMSM

根据专家对方案的信息熟悉程度，给出置信水平。下面将介绍CLIFGMSM和CLIFWGMSM。

定义5 设si=(Spi,Sqi)(i=1,…,l)，Ii(0≤Ii≤1)为si的置信水平，如果

CLIFGMSM(t,κ1,…,κt)(〈s1,I1〉,…,〈sl,Il〉)=

(8)

则称CLIFGMSM为置信语言直觉模糊GMSM算子。

例1设〈s1,I1〉=〈(S5,S3),0.90〉，〈s2,I2〉=〈(S4,S2),0.88〉，〈s3,I3〉=〈(S6,S1),0.92〉，令t=1,κ1=1,κ2=2，则

(9)

CLIFGMSM的性质：

幂等性：如果〈si,Ii〉=〈s,I〉(i=1,…,l)，即si=s,Ii=I，则

GLIFGMSM(t,κ1，…,κt)(〈s1,I1〉,…,〈sl,Il〉)=Is

(10)

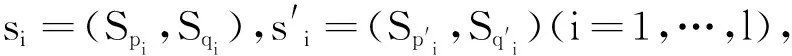
CLIFGMSM(t,κ1,…,κt)(〈s1,I1〉,…,〈sl,Il〉)≤

CLIFGMSM(t,κ1,…,κt)(〈s1′,I1〉,…,〈sl′,Il〉)

交换性：设{〈s1,I1〉,…,〈sl,Il〉}是1个语言直觉模糊数和它们的置信水平的集合，{〈t1,τ1〉,…,〈tl,τl〉}是{〈s1,I1〉,…,〈sl,Il〉}的任何一个排列，则

CLIFGMSM(t,κ1,…,κt)(〈s1,I1〉,…,〈sl,Il〉)=CLIFGMSM(t,κ1,…,κt)(〈t1,τ1〉,…,〈tl,τl〉)

(11)

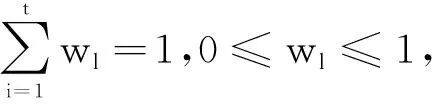
CLIFGMSM(t,κ1,…,κt)(〈s1,I1〉,…,〈sl,Il〉)=

(12)

则称CLIFWGMSM为置信语言直觉模糊加权GMSM算子。

例2设〈s1,I1〉=〈(S5,S3),0.90〉，〈s2,I2〉=〈(S4,S2),0.88〉,〈s3,I3〉=〈(S6,S1),0.92〉,w=(0.4,0.3,0.3)T为s1,s2,s3的权重向量，令t=2,κ1=1,κ2=2，则

(13)

CLIFWGMSM的性质：

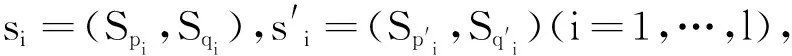
CLIFGMSM(t,κ1,…,κt)(〈s1,I1〉,…,〈sl,Il〉)≤

CLIFGMSM(t,κ1,…,κt)(〈s1′,I1〉,…,〈sl′,Il〉)

交换性：设{〈s1,I1〉,…,〈sl,Il〉}是1个语言直觉模糊数和它们的置信水平的集合，{〈t1,τ1〉,…,〈tl,τl〉}是{〈s1,I1〉,…,〈sl,Il〉}的任何排列，则

CLIFGMSM(t,κ1,…,κt)(〈s1,I1〉,…,〈sl,Il〉)≤

CLIFGMSM(t,κ1,…,κt)(〈t1,τ1〉,…,〈tl,τl〉)

(14)

4 决策方法

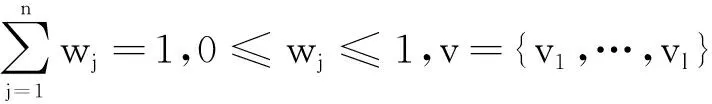
步骤2：用CLIFWGMSM对步骤1里的决策信息和置信水平进行聚合，得到矩阵a=(ski)m×l。

步骤3：用CLIFWGMSM对a=(ski)m×l里的行各自进行聚合。

步骤4：计算R(sk)(k=1,…,m)，得到最优方案。

实例：为了改善环境，某企业打算迁工厂需要选一个地方重新修建工厂，经过专家的前期考查有四个地方可选，这四个地方为{ε1,…,ε4}，三位专家{u1,u2,u3}，v1,v2,v3分别表示这四个地方的成本、距离和环境，专家用s=(Sp,Sq)对四个地方的成本、距离和环境进行评估，Sp,Sq∈Y[0,8]，同时给出置信水平，w={0.3,35,0.35}T为专家的权重向量，m={0.4,0.3,0.3}T为成本、距离和环境的权重向量，如表1。

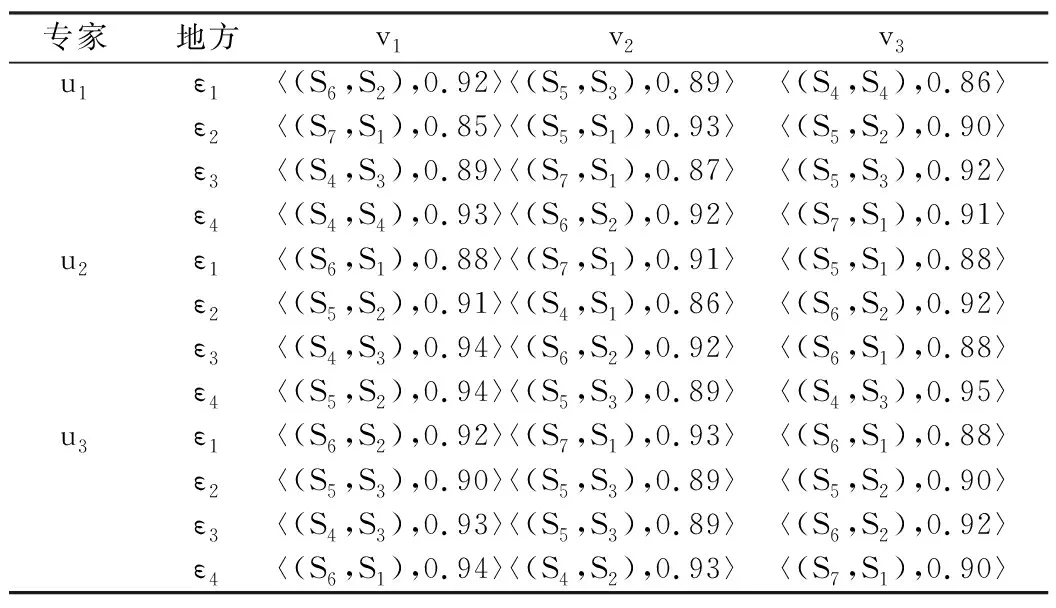
表1 矩阵

步骤1： 用CLIFWGMSM对表1里的决策信息和置信水平进行聚合，得到表2。

表2 矩阵Λ(ULIVIFCA)

步骤2：用CLIFWGMSM对表2里的行各自进行聚合，得到：

s1=(S1.022,S6.786),s2=(S0.775,S6.961),s1=(S0.845,S7.039),s1=(S0.928,S6.851)

步骤3：计算R(sk)(k=1,…,4),得到：

R(s1)=1.246,R(s2)=1.296,R(s3)=1.273,R(s4)=1.265

可以得到R(s1)=1.246最小，因此方案1为最优方案。

通过Liu等[19]介绍的基于WLIFMSM算子的方法计算得到四个方案的排序为s1>s4>s2>s3，得到排序和介绍的方法的排序略有不同，但方案1都是最优方案。本文介绍的方法考虑了因为一些限制专家对各个方案不一定完全熟悉，也就是给出了置信水平。GMSM算子是MSM算子的扩展，因此GMSM算子要更一般化，介绍的方法要比Liu等介绍的方法更切实可行。

5 结语

由于一些限制，专家不一定对方案的信息完全熟悉，因此考虑了置信水平，即专家对方案信息的熟悉程度,GMSM算子给出了方案属性之间的相互关联。因此给出了CLIFGMSM和CLIFWGMSM算子，同时给出了算子的性质。最后给出基于CLIFWGMSM算子的决策方法运用到实例中，选出最优方案，且和Liu等[19]介绍的方法进行比较，GMSM算子是MSM算子的扩展，介绍的方法考虑了因为一些限制专家对各个方案的信息不一定完全熟悉，因此本文介绍的方法要更切实可行。