基于连续管物模试验的高压气井压裂泵压预测*
2021-09-08刘辉熊勇富刘洋王荣屈剑峰龚杨
刘辉 熊勇富 刘洋 王荣 屈剑峰 龚杨
(1. 塔里木油田分公司油气工程研究院 2.川庆钻探工程有限公司井下作业公司)
0 引 言
储层改造是库车山前超深超高压高温气藏单井建产和提产的主要措施。但是在库车山前储层改造施工时,普遍存在泵压高、施工难度大的问题,改造液体在管柱中的摩阻性能是影响压裂设计和施工的关键参数,目前针对库车山前储层改造液体体系尚未开展系统的摩阻性能测试及分析。
国内外很多学者都对液体摩阻性能进行了理论和试验研究。国外学者P.S.SRINIVASAN等[1]早在1970年就通过大量试验数据回归了摩擦因数表达式,并推导出临界雷诺数计算公式;C.M.WHITE[2]在螺旋段的摩阻压降计算中引入迪恩数,发现螺旋管的临界雷诺数远高于直管临界雷诺数;C.C.OGUGBUE等[3]研究了不同液体在螺旋管中的摩阻性能,推导出压降计算公式。国内学者方清华[4]以CW公式为基础,提出了近似的显式方程。本文在前人研究的基础上,研制了大型连续管液体摩阻测试系统,将试验结果与流体力学原理相结合进行理论推导,建立了试验连续管-现场压裂管柱液体摩阻压降转换数学模型,以期为库车山前储层改造设计及施工提供指导。
1 技术分析
1.1 连续管液体摩阻测试系统
连续管液体摩阻测试系统的基本原理是:采用700型压裂车向试验用连续管中以不同排量注入改造液体,通过测量不同排量下连续管进、出口端压力,评价不同改造液体的摩阻性能。该系统主要包括泵注系统、配液及储液系统和试验管路(连续管)。泵注系统为700型压裂车,配液及储液系统为12 m3双搅拌器储液罐以及低压管汇,试验管路为ø31.8 mm×375 m、ø31.8 mm×1 050 m、ø31.8 mm×1 425 m等三套连续管盘管,可以自由切换管路长度。主要性能参数:ø31.8 mm连续管壁厚2 mm,油管钢级QT900、抗内压强度70 MPa。试验流程及所需设备如图1所示。

图1 连续管液体摩阻测试系统Fig.1 Coiled tubing friction test system
1.2 试验流程
(1)启动700型压裂车,连接配液罐,按试验要求的工作液配方进行配液。
(2)配液完成后检查管线、旋塞、传感器和流量计连接是否正确,根据试验项目开启相应的阀门、旋塞。(启用长度375 m连续管开启1、3、4号旋塞,关闭2、5、6号旋塞;启用长度1 050 m连续管开启2、5、6号旋塞,关闭1、3、4号旋塞;启用长度1 425 m连续管开启1、4、5、6号旋塞,关闭2、3号旋塞)。
(3)打开远程控制柜,开启摩阻测试程序,采集试验数据。
(4)打开安全阀并设置限压50 MPa。
(5)启动700型压裂车,按照试验方案开始试验,待每个排量台阶稳定后再提排量。
(6)试验完毕后用清水吹扫管路内的试验液体。
2 液体摩阻计算模型建立
试验用连续管的管径很小,且在试验中,当压裂液在缠绕于滚筒上的连续管中流动时,弯曲管产生的离心力会导致二次流现象[5],如图2所示。在二次流的作用下,弯曲管中液体的压耗损失总是大于直管[6],因此用连续管液体摩阻测试系统测得的液体摩阻与现场压裂施工中的摩阻压降误差较大,不能直接使用。为了将连续管内测得的液体摩阻压降转换为现场施工摩阻压降,需要结合流体力学原理进行理论推导,建立试验连续管-现场压裂管柱液体摩阻压降转换数学模型。本文在建模中假设试验液体为不可压缩流体,且液体的特征参数在管路流动过程中的变化忽略不计。

图2 弯曲管二次流现象Fig.2 “Secondary flow” phenomenon in bent pipe
2.1 流态判别
在研究液体摩阻性能之前,首先要判断液体类型以及液体在流动过程中的流态特征。根据流体力学原理,需要计算雷诺数来进行判断。通常改造液体为幂律流体,雷诺数可由下式[7]求出。
(1)
式中:ρ为液体密度,kg/m3;v为流速,m/s;d为管路内径,m;n为流体的流性指数;k为稠度系数,Pa·sn。
对于直井现场压裂管柱,可以通过式(2)计算临界雷诺数来判断压裂工作液的流态。
Ret=3 470-1 340n
(2)
对于本试验用连续管,可以通过式(3)计算临界雷诺数来判断液体流态。
(3)
其中:
α=47.9-153.8n+166.2n2-60.1n3
(4)
β=0.9n-0.5
(5)
式中:D为试验用连续管滚筒直径,m;d为试验用连续管直径,m。
当Re>Ret或Rec时,流态为紊流;当Re 若要研究不同液体在管柱内的流动压降,则需要得到管柱内壁对不同液体的摩擦因子。对于直井现场压裂管柱,管柱内摩擦因子可以由式(6)[8-13]计算,不受流体类型的限制。 (6) 式中:f为管柱内摩擦因子;a和b的值根据液体流态确定,当液体为层流时,a取16,b取1;当液体为紊流时,a、b值由式(7)和式(8)确定。 (7) (8) 对于试验用连续管,根据国内外学者建立的液体摩阻压降模型进行计算,但计算结果与试验结果误差较大,无法使用。因此,在流体力学公式基础上,假设试验和连续管内摩擦因子与a、b、Re、d和D均有关,结合压裂液连续管摩阻压降试验数据(见表1),回归推导出幂律流体和牛顿流体在试验用连续管中紊流流动时管柱内摩擦因子公式,分别如式(9)和式(10)所示。 表1 压裂液连续管摩阻压降试验数据Table 1 Coiled tubing friction pressure drawdown test data of fracturing fluid (9) (10) 当液体为层流时,可以采用式(11)[1]计算管柱内摩擦因子,不受流体类型限制。 (11) 液体在管路中的摩阻压降可以根据流体力学中圆形管液体压降计算公式进行计算,如式(12)所示。 (12) 联立式(6)、式(9)~式(12),可以推导出试验用连续管-现场压裂管柱液体摩阻转换系数。 当压裂液在试验用连续管中为层流时,转换系数Cc的计算式为: (13) 当压裂液在试验用连续管中为紊流时,转换系数Cw的计算式为: (14) 式中:at、bt、ac、bc分别为现场压裂管柱和试验用连续管的a、b值;Lt为现场压裂管柱长度,m;dt为现场压裂管柱内径,m。 确定了转换系数,就可以根据式(15)计算现场摩阻压降。 Δpx=ΔpsC (15) 式中:Δpx为现场摩阻压降,Δps为试验摩阻压降,C为转换系数。 选取库车山前一口压裂施工井(K2井)对转换模型的准确性进行验证。试验-现场摩阻压降转换结果如表2所示。 表2 试验-现场摩阻压降转换结果(排量2.0 m3/min)Table 2 Test-field friction conversion results (at displacement of 2.0 m3/min) 压裂施工管柱结构为:ø114.30 mm×9.65 mm油管+ø114.30 mm×8.56 mm油管+ø88.90 mm×9.52 mm油管+ø88.90 mm×7.34 mm油管+ø88.90 mm×6.45 mm油管+ø88.90 mm伸缩管+ø88.90 mm×9.52 mm油管+RD安全循环阀+RD循环阀+液压循环阀+E型阀+ø139.70 mm封隔器+ø73.02 mm×7.82 mm油管+筛管+接球器+电子压力计托筒组+ø73.02 mm×7.82 mm油管+电子压力计托筒组+管鞋。井底压力由井下压力计获得,据此可计算得到准确的液体管柱摩阻压降。 试验液体为K2井压裂施工时使用的质量分数0.4%的胍胶压裂液,流性系数n为0.16,稠度系数k为1.05 Pa·sn,试验排量为2 m3/min。井下压力计测得的压裂液管柱总摩阻压降为11.38 MPa,数学转换模型计算的总摩阻压降为11.56 MPa,两者误差在5%以内,说明数学转换模型可靠。 (1)研制的大型连续管液体摩阻测试系统配备三套不同长度连续管的试验管路,抗内压强度高,可以测定不同注入排量下改造液体在管内的摩阻压降。 (2)由于试验用连续管内径小、曲率大,所以液体在试验用连续管中流动摩阻压降与现场压裂施工摩阻压降存在差异。 (3)根据试验结果并结合流体力学原理,针对本套测试系统建立了试验用连续管现场压裂管柱液体摩阻转换数学模型,用该模型可以实现现场施工液体摩阻压降的准确预测。 (4)本文建立的转换模型适用于幂律流体,下一步将对牛顿流体建立相应的转换模型。2.2 管柱内摩擦因子
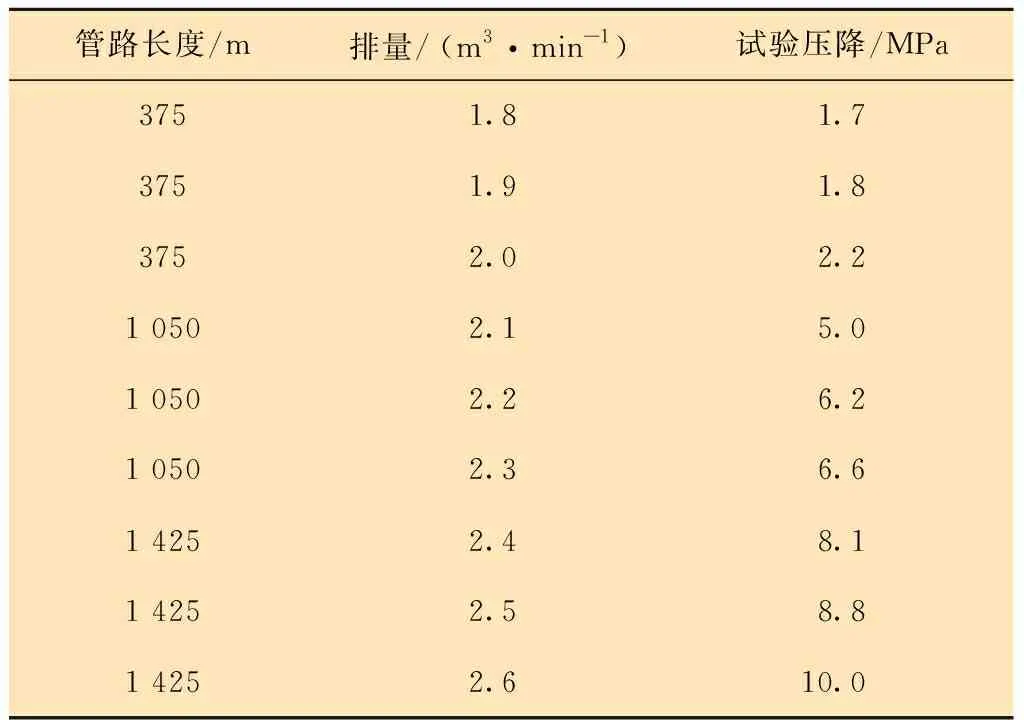
2.3 液体摩阻压降计算
3 实例验证
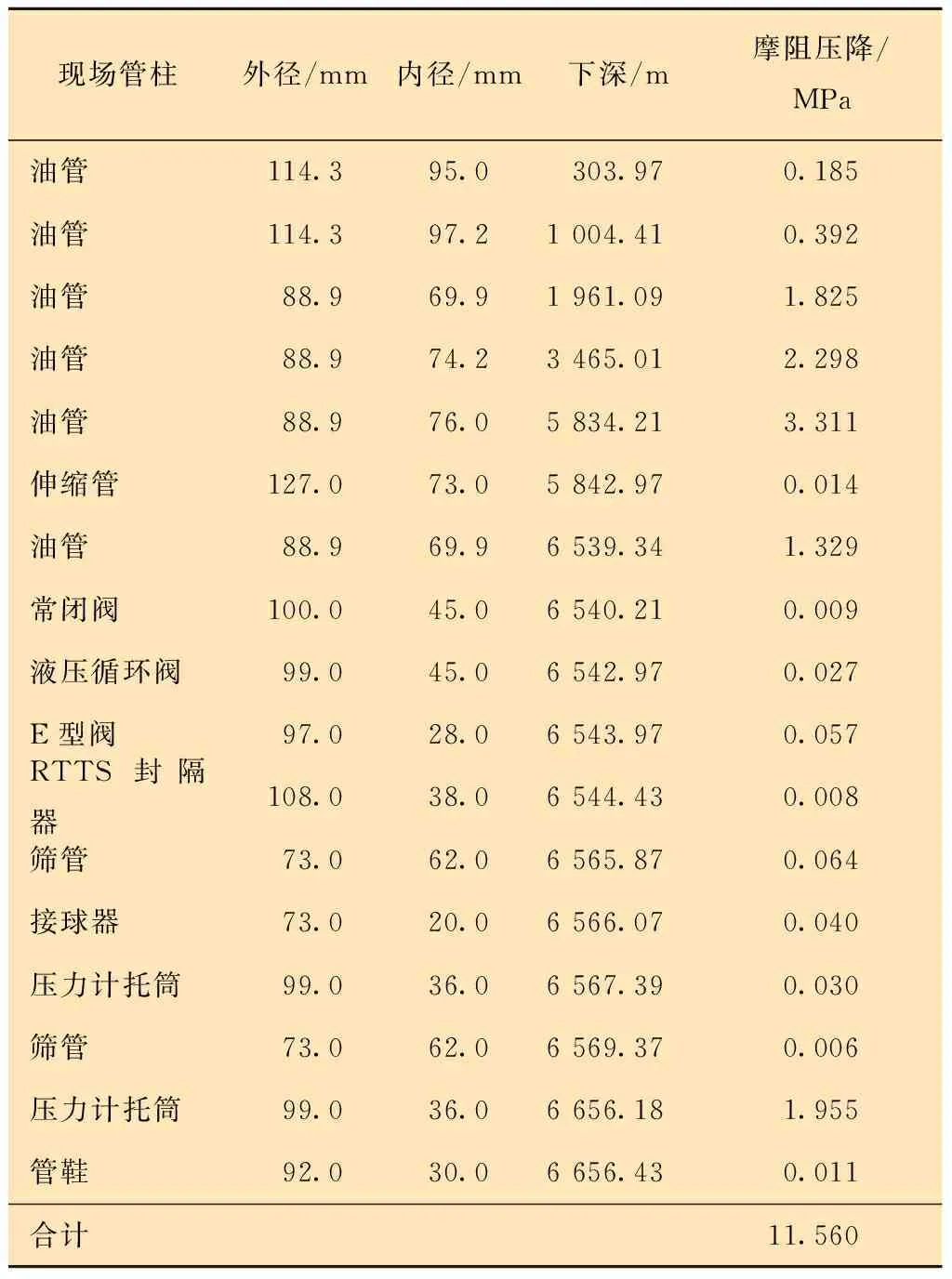
4 结 论
