一种改进的全卷积神经网络多聚焦图像融合研究

魏辉琪，刘增力

（昆明理工大学 信息工程与自动化学院，云南 昆明 650500）

0 引 言

日常生活中，人们在拍摄照片时不但要选择拍摄清晰的摄像机，而且希望所拍景物里所有物体都具有清晰的质量。但由于摄像机会受到景深的限制，无法将拍摄的所有目标都聚焦，造成一张照片会有聚焦和非聚焦的部分[1-3]。如何将两幅聚焦位置不同的图像融合到一起，并且使融合后的图像质量优良、细节信息丰富[4]，一直是多聚焦图像融合研究的热点。

2007年，Nencini F等人将曲率变换应用于图像融合，以期达到优异的视觉效果，实际融合效果优于使用Contourlet变换的融合算法。一些学者提出一种使用NSCT的多焦点图像融合算法以及一种将NSCT和空间频率激励脉冲与支架一起使用的图像融合算法。随着深度学习和迁移学习领域的发展，越来越多的学者将深度学习广泛运用到多聚焦图像融合中。由于卷积神经网络以生物神经元结构思想为起点，具备网络结构方便快捷和特征提取良好性的能力，很多学者将卷积神经网络（Convolutional Neural Networks，CNN）应用到图像融合任务中。有学者提出自动设置融合规则的方法，成功摆脱了手动设置融合规则的限制[5]。文献[6]和文献[7]采用了整体学习策略基于投票的方法进行图像融合。也有学者对卷积神经网络模型进行了相应改进[8]，提高了网络利用率，但仍然存在融合后图像边缘细节信息模糊这一缺陷。

为解决以上问题，本文提出一种改进的基于全卷积神经网络的多聚焦图像融合算法。采用鲁棒性主成分分析法（Robust Principal Component Analysis，RPCA）对原数据集进行特征提取；在网络特征提取部分采用更小的网络结构，达到提取更多特征信息的目的的同时减少了网络层级；将全连接层换为全卷积层，通过softmax层对图像进行分类，最后通过设置分类器防止样本偏移；通过设计的网络结构对数据进行训练，最终得到决策图，有效避免了细节信息丢失以及运算速率这一缺陷。

1 鲁棒性主成分分析法

鲁棒性主成分分析法是Karl Pearson等人提出的一种统计方法。它最主要的功能是帮助人们优化数据和筛选数据，目前在数学建模和机器学习等领域被广泛使用[9-11]。鲁棒主成分分析法可以良好地分离多聚焦图像中的聚焦信息和非聚焦信息，达到保留图像细节信息的目的。将多聚焦源图像经RPCA处理后的结果表示为：

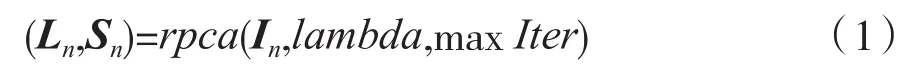
式中：Ln表示低秩分量；Sn表示稀疏分量；源图像A和源图像B表示为n=A,B；rpca(In,lambda,maxIter)表示图像的RPCA分解；lambda表示代价函数中稀疏误差项的权重。本文将lambda设为为输入矩阵In的行数，tol设为10-7，maxIter设为1 000。

RPCA将输入数据矩阵分解为低阶主成分矩阵和稀疏矩阵。分解时间受输入数据矩阵的矢量格式影响。本文首先在RPCA分解模型下对多聚焦图像I∈Rm×n进行向量格式转换，分解后得到D∈Rmn×1表示输入矩阵。为了获得低秩矩阵A∈Rmn×1和稀疏矩阵E∈Rmn×1，需要对输入矩阵D∈Rmn×1进行RPCA分解，因RPCA分解模型分解后的低秩矩阵和稀疏矩阵图像大小需保持和源图像一致，因此还需对低秩矩阵A∈Rmn×1和稀疏矩阵E∈Rmn×1进行向量转换，最终得到格式为A∈Rm×n、E∈Rm×n的低秩矩阵和稀疏矩阵。

本文对“时钟”图像进行RPCA图像分解，分解结果如图1所示。由图1可以看出，两幅源图像中，稀疏矩阵的显著信息位置和源图像的聚焦区域位置几乎对应。然而，在多聚焦图像融合中，融合图像是将两幅源图像的聚焦区域信息最大化提取之后进行合并，因此，多聚焦图像融合问题可以转化为RPCA分解模型中稀疏矩阵显著信息位置的选择和提取最大化的问题。因RPCA分解模型分解后的稀疏矩阵具有良好的鲁棒性，符合多聚焦图像融合中聚焦和细节信息保留最大化的要求，有利于融合图像质量的提高[12]。

图1 多聚焦图像“时钟”的RPCA分解效果图

2 本文方法

2.1 数据集预处理

本文对数据集预处理的方法采用了指定区域采样法的思路。该方法是将原清晰度图像数据集通过滤波器模糊后，在指定位置进行块提取和分割，得到以该图像块为中心的模拟多聚焦图像。方法原理如图2所示。

图2 指定区域采样法原理图

PASCAL VOC是一种公认的图像数据集基准，总共包含20类数据类型，类别包括动物、桌椅板凳及交通工具等。本文挑选了数据集中的4 000余张图片用于制作图像数据集，尺寸都标注为256*256。首先对每张图片做高斯模糊处理，模糊处理半径选为3，其次随机截取模糊处理前的图像的某一区域的图片，最后将截取的部分区域与未进行模糊处理的相同区域进行替换，模拟出交叉模糊的方式，使得数据集更接近于真实的多聚焦图像，使算法可以验证多组且聚焦区域不同的多聚焦图像。

2.2 网络结构

本文提出的网络模型，在经典的全卷积神经网络模型上进行了改进，整个网络结构如图3所示。

图3 网络结构图

模型在特征提取部分采用3个卷积层和1个池化层。因多聚焦图像在融合时只用提取到聚焦以及非聚焦重要信息，因此3个卷积层和1个池化层足以获得所需的特征信息，如图4所示。

图4 特征提取部分网络示意图

图像经过最大池化层压缩后进入全卷积层，如图5（b）所示。普通卷积神经网络在对图像识别时得到的是聚焦信息与非聚焦信息的概率分布；而全卷积神经网络识别的结果是聚焦图像和非聚焦图像，图像到图像的传输可以使得整个网络在训练时的运算时间有所降低。

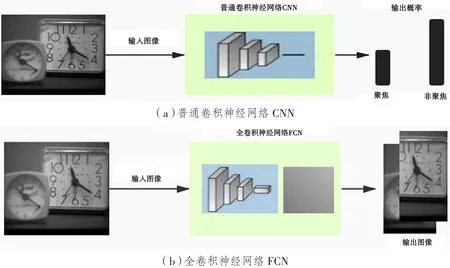
图5 不同网络中聚焦非聚焦识别过程

最终通过转置卷积恢复图像大小，通过softmax层以及权重设置进行像素分类。像素分类器可以确定聚焦、非聚焦像素的类别，达到防止样本偏移的目的。

全卷积神经网络结构参数如图6所示。可以看出，本算法所训练的网络结构相较于以往的全卷积神经网络结构而言层级更少。另外，本文网络所用的卷积核大小为3×3，步长为1；池化层核的大小为2×2，步长为2。实验表明，卷积核的选择不宜太多或者太少，分别会造成分类结果较差和像素点提取过少，达不到特征信息提取的目的。池化的本质是数据压缩，一方面抑制响应较低的信号，降低噪声；另一方面减少需要学习的参数，降低网络规模，在空间上实现感受野的增大，有利于使用较小的卷积核实现更大尺度上的特征学习。

图6 全卷积神经网络结构参数

2.3 网络训练

将预处理好的数据集输入到网络结构中，开始训练。本文训练的基础学习率为0.001，每训练一次共4轮，每轮迭代393次，共1 572次。训练导出的训练曲线如图7所示。从图7可以看出，当训练达到700次左右，损失降到最低并且在一定范围内浮动，准确度达到最高并且在一定范围内浮动。

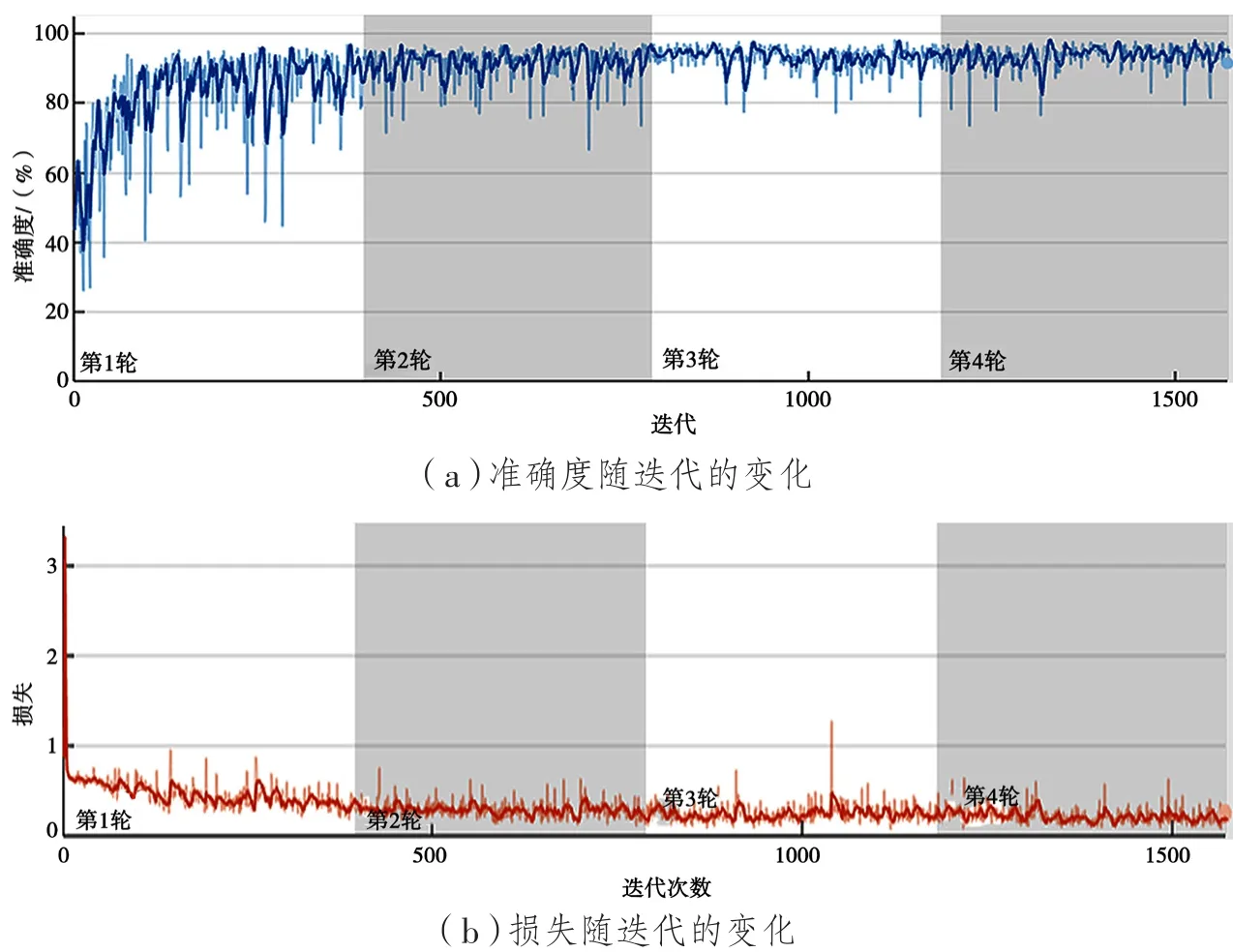
图7 全卷积神经网络网络训练图

2.4 本文融合过程

通过RPCA对图像进行特征提取，之后利用全卷积神经网络模型进一步获得特征以及决策图，以决策图为依据对图像进行最终的融合。整个融合过程如图8所示。

图8 基于RPCA的卷积神经网络图像融合过程

融合过程主要分为3个步骤。

（1）网络训练。选择合适的网络参数；确定卷积层、池化层以及全卷积层的输入与输出，根据网络特性选择损失函数和激活函数；确定网络训练所需的学习率和总迭代次数等。

（2）用全连接层替换卷积层后，输入图像的大小就可以不受限制。可以一次性输入网络，根据图片所有位置的检测目标概率得到功能图。

（3）生成决策图。在本文算法中，网络首先对图像像素进行分类，输出焦点图。得到焦点图后，通过二值化得到二值图，进一步得到初始决策图。对初始决策图进行细节信息处理后得到最终决策图。

3 实验结果与分析

为验证算法的有效性，将本文提出的融合算法与其他4种算法进行比较。其他算法分别是基于离散小波变换（DWT）[17]、非下采样剪切波变换（NSST）[18]、非下采样轮廓变换（NSCT）[19]以及卷积神经网络（CNN）[16]。

作为验证融合图像质量的两种重要方式，主观评价和客观评价缺一不可。本文采用主观肉眼以及客观指标评价两种评价方式进行评价。客观评价指标有信息熵（H）、互信息（MI）[13]、结构相似度（SSIM）[14]以及边缘保持度融合质量指标QAB/F[15]。通过以上指标对本文的算法进行验证。

信息熵的定义为：

式中：N为灰度级；Pi为概率。

互信息量MI定义为：

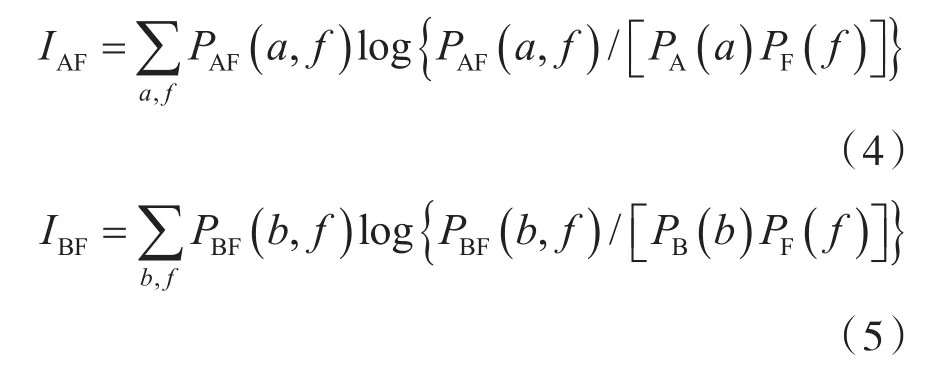
式中：a、b、f为源图像A、B和融合图像F的像素灰度值；PA(a)、PB(b)、PF(f)为概率密度函数；PAF(a, f)、PBF(b, f)为联合概率密度函数。

结构相似度定义为：

式中：F为融合图像；A为源图像；μa、μf为A和F间的均值；σa、σf为A和F间的标准差；covaf为A和F间的协方差；α，β，γ分别表示亮度、对比度及结构三部分的比例参数；c1，c2，c3表示三个常数。

边缘保持度融合质量指标QAB/F的定义为：

式中：M和N是图像尺寸；QAF(n,m)、QBF(n,m)分别是融合图像相对于原始图像A和B的边缘保持值；ωA(n,m)、ωB(n,m)是边缘强度的函数；QAB/F∈[0,1]表示融合图像相对于原始图像A和B的总体数据保留，其值越大，融合图像质量越高。

3.1 主观评价

本文选取了4种融合方法测试图像来进行算法验证。图像“时钟”的融合结果如图9所示。其中，图9（a）和图9（b）分别为聚焦源图像A和聚焦源图像B；图9（c）、（d）、（e）、（f）、（g）分别为算法DWT、CNN、NSST、NSCT以及本文算法的融合结果。

图9 “时钟”融合结果图

从“时钟”实验融合结果可以看出，基于DWT、NSST以及NSCT算法融合后的图像都出现了不同程度的“伪影”现象，融合效果不理想。而CNN算法的结果则可以看到融合后的边缘细节部分出现了丢失。

为更方便、清晰地观察本文网络结构算法与卷积神经网络算法融合图像后的效果差异，使用对比软件对实验结果“时钟”图分别在基于卷积神经网络（CNN）算法与本文全卷积神经网络（FCN）算法产生的融合结果进行差异对比，可以清楚地看出结果的差异，如图10中红色区域所示。

图10 “时钟”融合图CNN与FCN对比差异

3.2 客观评价

表1列出了使用上述4个客观评价指标以及运算速度针对5种不同融合方法的评价结果。从实验结果可以看出，本文提出的算法的互信息、结构相似度等指标都高于其余4种方法，即使在图像清晰度以及互信息方面与目前运用较广泛的CNN算法相差不多，但是在运算速率上大大提升，说明了本文算法的优越性和有效性，更具有应用价值。

表1 针对“时钟”融合图像的评价指标结果

4 结 语

本文提出了一种改进的全卷积神经网络多聚焦图像融合算法，与传统算法RPCA相结合，在图像特征信息过程提取到了更多有用信息。网络结构轻便、快捷，使得算法在整个融合过程既保证了融合质量的提升又节省了运行时间。实验结果表明，该算法在保持边缘信息、整体融合图像的质量以及运算速度上有一定提升，具有一定的研究价值。