圆柱与扭转柱杆件受电弓气动与噪声研究
2021-09-08李启良李卓明
李启良,李卓明,魏 峥
(1.同济大学上海地面交通工具风洞中心,上海 201804;2.中国空气动力研究与发展中心气动噪声控制重点实验室,四川绵阳 621000;3.泛亚汽车技术中心有限公司上海 201201)
受电弓是高速列车从接触网上获取电能的关键装置,其良好的气动性能有利于弓网系统的稳定和高受流质量[1]。当前的受电弓杆件存在众多圆柱形结构。当高速气流通过时,其两侧产生周期性交替的涡脱落,导致杆件表面产生剧烈脉动压力,进而向车内外辐射强烈噪声。有效控制受电弓杆件流动,就能提升其气动和噪声性能。
近年来,研究人员基于准二维的圆柱外形强加三维几何扰动的控制思想来改善传统圆柱气动性能。Jung等[2]设计出扭转柱外形以达到控制流场的目的。扭转柱是由椭圆形的横截面沿轴向旋转而成。研究表明,与圆柱相比,这种空间三维曲面在平均阻力和脉动升力分别降低13%和96%。Kim等[3]发现,无论扭转柱处于层流还是湍流状态,与圆柱相比,其气动力均有降低。通过改变截面纵横比和轴向波长,得到气动阻力最小的最优参数组合。Wei等[4]探究了沿扭转柱轴向不同截面上产生的局部气动力,进而发现其三维涡结构产生的气动阻力功率谱密度具有谐波特性。作者[5]采用基于聚类降阶方法分析扭转柱尾流特征,梳理出主要涡流结构。
为了研究柱体之间相互干扰,以明确受电弓系统气动与噪声性能。研究人员开展了受电弓系统预测方法、流场与噪声性能分析与优化工作。为提高计算效率,Tan等[6-7]建立了受电弓系统子域模型,探究了5种湍流模型,发现大涡模拟具有最高的计算精度。在此基础上,探究受电弓流场的漩涡结构以及主要部件的气动噪声发现,受电弓的涡流结构随时间变化并具有一定的周期性,而声源强度主要分布在底部框架、绝缘体、平衡杆、上臂杆和下臂杆。Wang[8]通过大涡模拟进行翼缘仿生优化,即在传统受电弓滑板下表面均匀设置半径3.2 mm的小半圆形凹槽。研究结果表明,优化后的受电弓能够有效降低受电弓尾涡脱落,从而降低气动噪声。
本文结合时速400 km·h-1高速列车受电弓开发需求,探索扭转柱杆件受电弓系统气动与噪声性能,并与圆柱杆件进行对比,评估两者差异。在此基础上,采用基于聚类降阶方法深入分析不同类型杆件尾迹流场,探究其内部转换机制,梳理其与噪声关系,为相关研究提供方法指导、产品开发提供借鉴。
1 仿真方法
1.1 几何模型与网格划分
计算采用1:8缩比受电弓系统模型,其由滑板、支架、上臂杆、推杆和下臂杆组成,如图1a所示。对原受电弓系统模型进行改型设计,将主要杆件设计成扭转柱,见图1b。图中,P1~P5为空间测点。
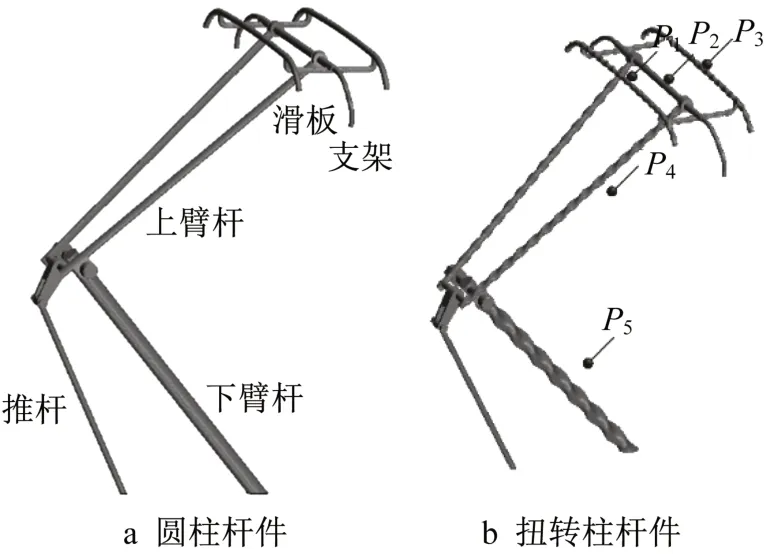
图1 受电弓几何模型Fig.1 Geometry of pantograph
首先将受电弓系统安装在1:8缩比三车编组模型高速列车上。高速列车长10.57 m、宽0.42 m和高0.51 m。将高速列车放置在半无限大虚拟风洞中,其长(L)、宽(W)和高(H)分别为18.5、5.5和2.5 m,如图2a所示。采用切割体和边界层网格策略划分全域,并在受电弓和车身附近进行网格加密,远离车身网格较为稀疏,靠近车身网格较密,两者之间逐层过渡,如图3a所示。最小面网格集中在受电弓,其大小为1 mm;车身和转向架面网格尺寸约为3 mm。体网格最小尺寸为1.5 mm,最大尺寸为48 mm。在车身和地面上以1.2为增长率生成5层边界层,总厚度1 mm。全域体网格总数约为4 650万个。
为了提高计算效率,采用子域方法进行受电弓系统气动与噪声预测。该方法为众多研究人员所采纳,有一定准确性和合理性[6-9]。子域模型以列车顶部为底面,在受电弓系统上、下游、两侧和顶部创建长1.2 m,宽0.35 m,高0.5 m的子域,如图2b所示。按照与全域相同的体网格划分策略,获得如图3b所示关键截面体网格。面网格尺寸为1 mm,体网格最大尺寸为6 mm。在受电弓系统和车顶以1.2的增长率,生成25层边界层网格,网格总厚为1 mm。子域体网格总数约为300万个。

图2 计算域(单位:m)Fig.2 Computational domain(unit:m)
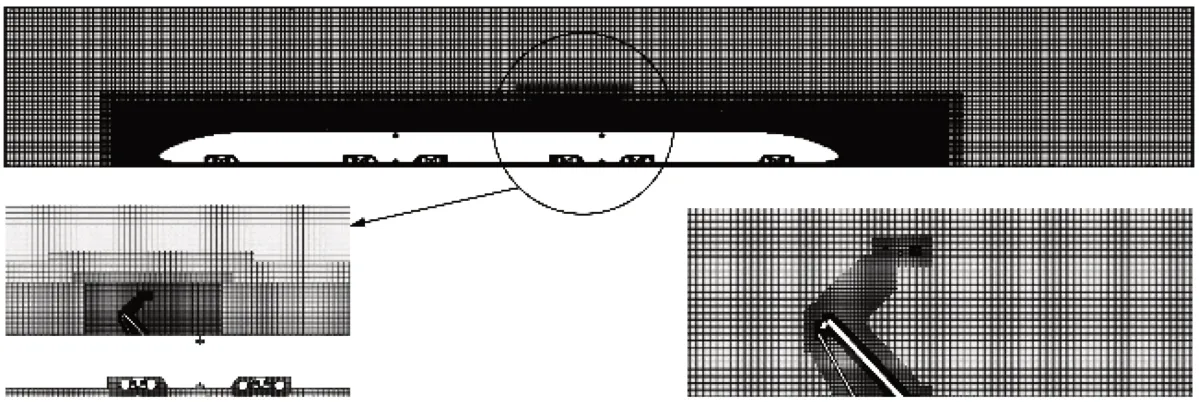
图3 关键截面体网格Fig.3 Volume grids of key plane
1.2 气动仿真方法
在全域计算时,计算域入口为速度入口,给定均匀来流速度U∞=400 km·h-1。出口设置为压力出口,给定压力0。顶面、侧面为对称,地面、车身表面为无滑移壁面。使用SSTk-ω湍流模型[10]求解高速列车定常流场。计算收敛后,输出子域四周截面的速度分量和压力,并将其作为子域计算的边界条件。子域底面和受电弓设置为无滑移壁面,入口、侧面和顶面均为速度入口,出口为压力出口。所需速度和压力均来自全域计算结果。首先使用SSTk-ω湍流模型得到非定常流场的初始准定常解,然后使用大涡模拟[11]计算非定常流场,时间步长为1×10-5s,每个时间步迭代10次。10 000个时间步后流场进入稳定,继续迭代10 000步,并同时采集关键截面和受电弓气动数据。
1.3 聚类降阶分析方法
Kaiser等[12]提出了一种基于聚类分析的降阶模型(cluster-based reduced-order modelling,CROM)方法。聚类算法通过识别相对均匀的快照集合,对状态空间进行低维描述。首先将快照依据快照之间的相似性分成几簇,其次决定簇间的转换可能性,最后各个簇依据此进行排序和区分。
在具体分析时,快照被划分为给定数量的子集,被称为簇Ck。本文取K=10,既能够求解主要的簇间转换过程,又满足所需的数值精度。属于某一簇的所有快照的平均决定此簇的代表性中心,被称为质心ck。提取所有质心就能够描述流场的动态变化。聚类可能性分布直接由快照数据获得,其关键是确定簇转换矩阵(cluster transition matrix,CTM)和簇距离矩阵(cluster distance matrix,CDM)。CTM为一个时间步长的转换概率矩阵,CDM则衡量了簇间转换轨迹的长度。通过深入分析CTM,并由此建立识别状态间的转换过程Markov链,从而能够提取潜在的物理机制。
1.4 远场噪声仿真方法
直接法和混合法是目前气动声学的计算方法。由于直接法需要巨额计算资源,因此在目前的计算条件下,大多数气动声学的计算均采用混合法。基于FW-H方程[13]的声类比法是目前应用最广泛的气动噪声计算方法,可以得到远场测点处的声压级频谱和总声压级。
2 气动分析
由于尚未开展圆柱和扭转柱杆件受电弓气动和噪声试验,故无法对此进行直接对比。为此开展了雷诺数为20 000的圆柱气动计算,平均阻力系数、脉动升力系数和斯托拉哈尔数的仿真值与试验值较小的差异表明当前仿真方法的可靠,详见文献[5]。
2.1 气动力
图4为受电弓所受阻力和升力的瞬时变化曲线。气动力在某一时均值附近振荡,圆柱杆件的受电弓所受阻力小于扭转柱杆件的受电弓,他们平均阻力分别为41.32和43.67 N。由图4b可知,扭转柱杆件大大削弱了受电弓所受的平均升力和脉动升力。平均升力由1.68 N降低至0.84 N(方向向下),脉动升力由2.11 N降低至0.58 N。可见,从气动力角度来看,扭转柱杆件对改善受电弓运行稳定性和受流质量有积极作用。但从弓网耦合动力学角度,仍需要从刚度和振动方面进行深入分析,从而全面评估扭转柱杆件对受电弓运行稳定性和受流质量的效果。
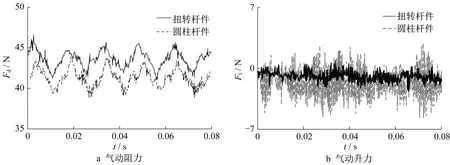
图4 瞬时力Fig.4 Instantaneous forces
2.2 降阶分析
基于大涡模拟计算采样得到的x=1.2 m平面(图2)的流场数据,利用CROM分析并识别不同杆件受电弓尾迹主要流动结构,试图揭示其复杂的非定常流动转换机理。
对采集到10 000个时间步的速度数据进行本征正交分解,然后对前20阶模态系数进行CROM分析。经k-means算法分簇后,得到簇间的动态转换过程的CTM和CDM,如图5所示。据此可获得圆柱杆件的受电弓尾迹流场的三条闭环转换路径:①C1→C2→C3→C4→C1,②C3→C4→C5→C6→C7→C8→C3,③C7→C8→C9→C10→C7;扭转柱杆件的受电弓尾迹流场的三条闭环转换路径:①C1→C2→C3→C4→C1,②C3→C4→C5→C6→C3,③C6→C7→C8→C9→C10→C6。这些转换路径,常被称为Markov链(图6)。

图5 CTM和CDM(上:圆柱;下:扭转柱)Fig.5 CTM and CDM(Top:circular cylinder;bottom:twisted cylinder)

图6 Markov链Fig.6 Markov chain
对于第一条转换路径,圆柱杆件与扭转柱杆件都是相同的。第二条转换路径并不相同,圆柱杆件从C6向C3转换时需先后经过C7和C8,而扭转柱杆件则直接从C6转向C3。圆柱杆件的第三条转换路径起止于C6,而扭转柱杆件则起止于C7。
进一步分析圆柱杆件和扭转柱杆件的转换路径中各单元的速度分布,如图7所示。对于圆柱杆件的第一条转换路径,截面侧向速度呈现显著变化对应的位置是下臂杆。从云图的变化可以看出,虽然圆柱以一定角度倾斜,但仍呈现出典型圆柱扰流的卡门涡街的流动结构。然而,在扭转柱下臂杆尾部典型单一的卡门涡脱落消失,取而代之的是更为复杂的涡脱落行为:上鞍面、下鞍面和节点面均出现涡脱落,存在涡脱落强度、相位和涡间相互作用。正是这样涡结构的变化,可使远场噪声尖峰被削减,但可能增加宽带噪声。对于圆柱形的上臂杆,该转换路径对应的侧向速度变化不大,但仍能初步判断在高度方向存在单一方向的涡流。然而,扭转柱的上臂杆在高度方向存在明显的正负交替涡流。对于圆柱滑板,在左右两侧呈现正负交替的涡流;但扭转柱滑板,却是上下才出现正负交替的涡流。

图7 簇质心速度云图Fig.7 Centroid velocity contour of cluster
对于第二条转换路径,圆柱杆件的涡流转化路径更长,但有明显差异的也仅是圆柱形下臂杆,其在高度方向存在单一的上下正负交替的涡流。扭转柱杆件的涡流转化路径稍短,差异最大的是其下臂杆存在多个上下正负交替的涡流。圆柱杆件的第三条转换路径比扭转柱杆件稍短,其流动结构的典型变化也在下臂杆。
3 噪声分析
为研究受电弓在空间中产生的声压级(SPL)大小,在距离模型中心线7.5 m、地面上方1.2 m处,坐标分别为r1(1 m,-7.5 m,1.2 m)、r2(1.2 m,-7.5 m,1.2 m)、r3(1.4 m,-7.5 m,1.2 m)分别布置远场测点,如图8所示。

图8 远场测点位置(单位:m)Fig.8 Positions of receivers(unit:m)
因r3和r1与r2频谱图极其相似,为此图9仅比较了不同受电弓的r2测点声压级频谱。从图中可以看到,1 000~3 000 Hz频段的噪声能量较高,两种受电弓在1 200~2 000 Hz左右分别出现峰值。扭转柱杆件的受电弓削弱了第一个峰值,由80 dB(计权,全文同)降至72 dB,但第二个峰值变化不大,均约为72 dB左右。另外,圆柱杆件的受电弓在3 200 Hz左右出现一个明显的尖峰,其峰值声压级约为70 dB。该峰值在扭转柱杆件的受电弓中消失。计算其总声压级发现,扭转柱杆件的受电弓总声压级为88.5 dB,比圆柱杆件的受电弓低1.5 dB,有明显降噪效果。
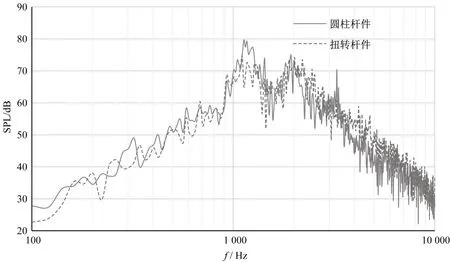
图9 r 2声压级频谱图Fig.9 Sound pressure spectra of r 2
为了明确1 200 Hz和3 200 Hz的降噪机理,分别在受电弓滑板、上臂杆和下臂杆布置监测点(图1b)。从图10所示的主流方向速度的功率谱密度(PSD)分析发现,位于圆柱滑板的测点P2在3 200 Hz存在明显尖峰,更换成扭转柱形状后,该测点的尖峰消除。位于圆柱形上臂杆的测点P4在1 200 Hz附近有驼峰,更换成扭转柱形状后,该测点的驼峰消除。可见,这些峰值的消失归根于圆柱更改为扭转柱后周期性卡门涡街被消除。
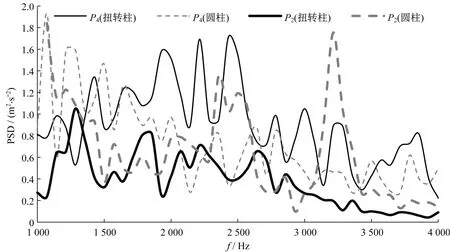
图10 P 2和P 4速度功率谱密度Fig.10 Power spectral densities of velocities for P 2 and P 4
4 结论
本文对圆柱、扭转柱杆件的受电弓进行气动与噪声数值仿真并对比二者性能,结论如下:
扭转柱杆件的受电弓与圆柱杆件的受电弓相比,虽然平均阻力稍有增加,但所受平均升力由1.68 N降低至0.84 N(方向向下),脉动升力由2.11 N降低至0.58 N。从气动力角度来看,对改善受电弓运行稳定性和受流质量有积极作用。
通过CROM分析可得两种受电弓的尾流场均存在三条闭环转换路径。圆柱杆件的第一条转换路径与圆柱杆件相同,但第二条稍短,而第三条稍长。当下臂杆由圆柱变为扭转柱时,其尾部由单一涡流向多个正负交替涡流转变。
圆柱杆件的受电弓在3 200 Hz左右出现一个明显的峰值,其峰值声压级约为70 dB,该峰值在扭转柱杆件的受电弓中消失。扭转柱杆件的受电弓总声压级比圆柱杆件的受电弓低1.5 dB,有较好降噪效果。
作者贡献说明:
李启良:理论和仿真指导,文章初稿修改和终稿审阅。
李卓明:文章修改。
魏峥:建模和仿真计算,数据处理,初稿撰写。
