小波包和Apriori算法燃气调压器故障诊断与预警

孙明远， 郝学军

(北京建筑大学 环境与能源工程学院， 北京 100044)

1 概述

国内外学者对燃气调压器故障诊断的方法有了阶段性进展[1-2]，但在燃气调压器故障预警方面的研究仍相对匮乏。高-中压燃气调压器运行参数类型众多，多变量之间的相关系数与典型故障之间存在一定的关联度，准确找出其关联对实现高-中压燃气调压器故障诊断与安全预警至关重要。因此，本研究采用小波包算法与Apriori算法相结合的方法实现高-中压燃气调压器的故障诊断预警。

2 研究概况

本文的研究对象是高-中压燃气调压器，型号为FL-BP的间接作用式轴流式调压器。

调压站调压工艺流程见图1。为了方便开展对调压器故障诊断预警的研究，除去调压站内已有可获取的监测数据类型外，通过外加传感器自行对监测数据类型扩展到了8种，监测的变量类型见表1。表1中调压支路运行调压器进口压力p1、调压支路运行调压器出口压力p2和调压支路工况流速v这3个量的传感器监测点分别见图1中点1、点2和点3。

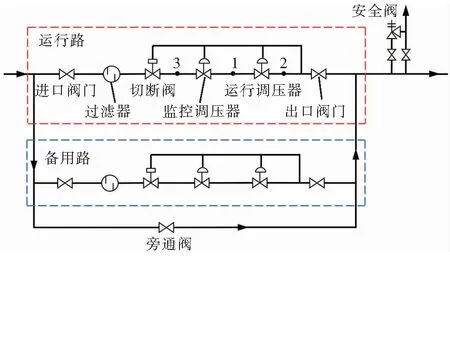
图1 调压工艺流程

表1 监测的变量类型

运行调压器有4种压力：运行调压器的进口压力p1；运行调压器的出口压力p2；由进口压力p1经过指挥器过滤、稳压后得到的指挥器稳定压力ps；负载压力p3，又称为中间压力，指由指挥器稳定压力ps和出口压力p2经调压弹簧相互作用调定的一个压力。

通过外加传感器可以测得调压支路工况流速v和运行调压器阀位相对开度K2。

通过大量前期调研与数据分析可知，调压器往往在冬供期间(11月15日至次年3月15日)因用气量大容易在运行过程中出现异常，而非冬供期间天然气用量小，故障概率随之减小甚至为0。因此，本文选取某市4个进口压力为高压B级、出口压力为中压A级的调压站，在2017—2018年和2018—2019年两个冬供期间部分日期的历史运行数据作为原始数据，共挑选了147 d，挑选的数据包括调压器正常运行的数据和出现各类故障的数据。燃气调压器典型故障分为4类：用气低谷出口压力偏高、用气高峰出口压力偏低、主阀喘振和指挥器喘振。根据不同种类故障的严重程度，分为预警和报警两种级别。预警表示调压器暂时没有发生故障，但未来大概率会发生故障，应当予以提示检修；报警表示调压器已发生故障，应立即对其进行检修。

本研究以1 d的数据为1组，1组中有出口压力p2、负载压力p3、工况流速v和运行调压器阀位相对开度K2这4种变量，每1种变量以1 d 中00: 00—23: 59为周期，每1 min记录1个数据。每组共有5 760个数据，总共147组。数据统计见表2。

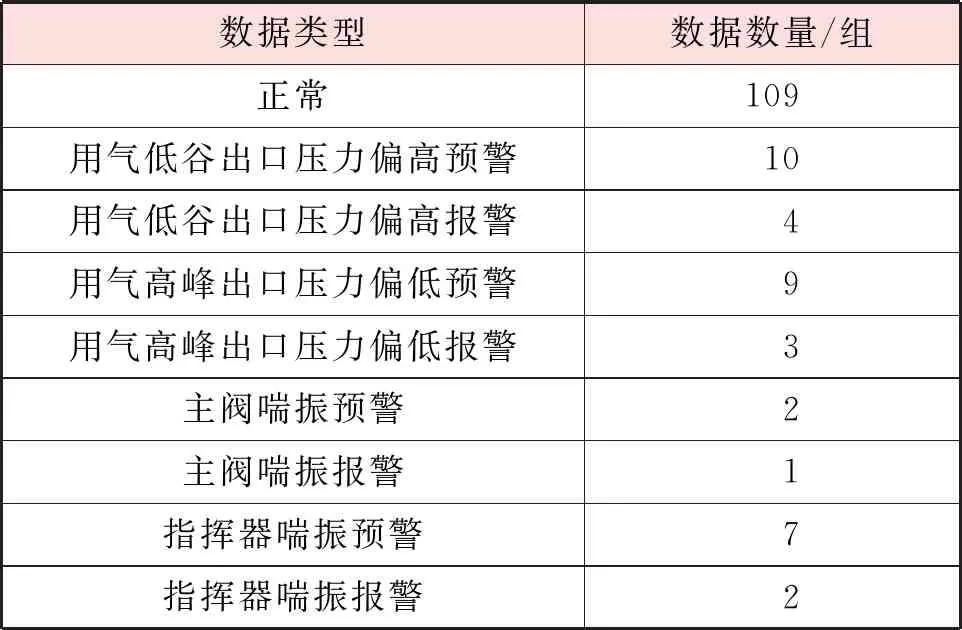
表2 数据统计

3 小波包频带能量值

3.1 小波包算法理论

在信号处理过程中，小波包算法会对信号进行频带分解，将信号中的低频谐波部分连续分解为高频信号和低频信号，同时还把上层高频谐波部分再一次分解为高频信号和低频信号，从而把频段分解得更加精细。以3层分解为例，小波包分解结构见图2。图2中，S是原始信号序列，L是低频信号序列，H是高频信号序列，最末尾数字是信号分解层数。

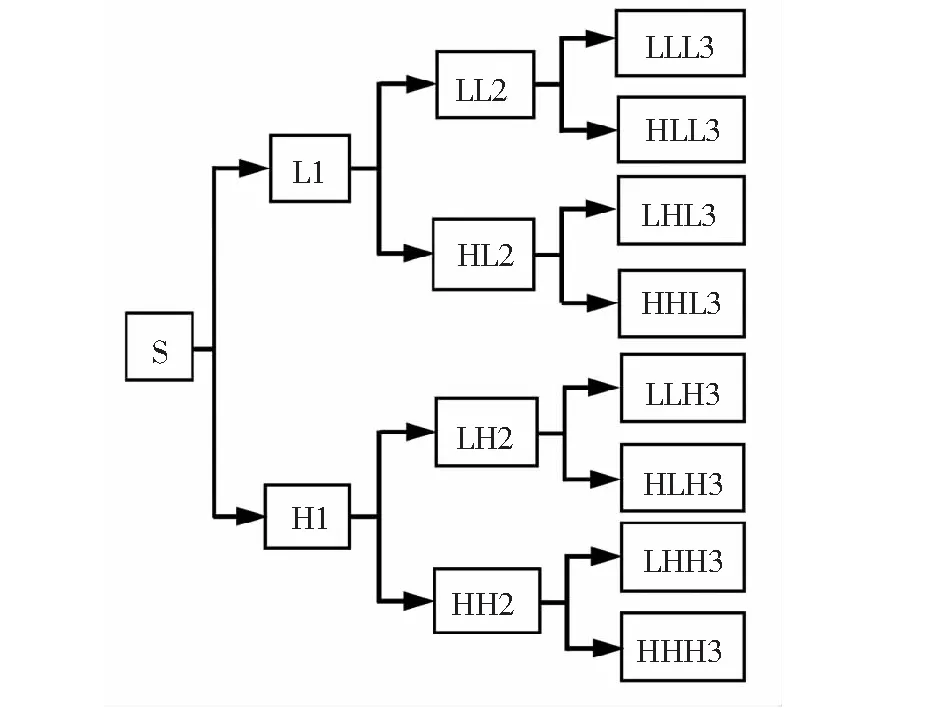
图2 小波包分解结构

小波包具有能量守恒的物理特点[3]，因此，当机械故障发生时，某些频带的能量信号必然会发生变化，通过分析这些频带能量值的变化可以对调压器的不同故障类型进行有效识别。在调压器实际运行工况下，由于压力信号是不断波动变化的，因此，对采集到的调压器出口压力p2以及负载压力p3这2种时域信号(随时间变化的动态信号)，应用小波包算法分解为频带能量值这种频域信号(随频率变化的动态信号)，从而实现故障诊断预警。

根据图1可以看出，每个压力信号经3层分解后最终将得到8个频带特征能量值，记为Ei(i=1～8)。分解出的E1是低频能量值，其代表系统的低频波动强度，波动幅度越大信号就越不稳定。因此，E1越大，调压器低频故障(调压器出口压力偏高或者偏低)就越严重。剩余的7个能量值则是高频能量值，其代表系统的高频波动强度，频率越高信号波动就越剧烈。因此，E2～E8越大，调压器高频故障(调压器喘振)就越严重。

3.2 频带能量值求解

每次在MATLAB中应用小波包算法，只调用1组原始数据中的1 440个出口压力数据所组成的序列和1 440个负载压力数据所组成的序列，147组原始数据共调用147次，选择db6小波函数[4]对其进行分解，求出压力信号的小波包频带能量值的分布情况，结果如下。

① 用气低谷出口压力偏高故障

预警的条件：p2的E1在(1.62,1.85]区间内；

报警的条件：p2的E1在(1.85, +∞)区间内。

② 用气高峰出口压力偏低故障

预警的条件：p2的E1在(1.62,1.8]区间内；

报警的条件：p2的E1在(1.8, +∞)区间内。

③ 主阀喘振故障

预警的条件：p2的E2～E8同时都在(0.52,0.86]区间内，且p3的E2～E8同时都在(0.4,0.95]区间内；

报警的条件：p2的E2～E8同时都在(0.86,+∞)区间内，且p3的E2～E8同时都在(0.4,0.95]区间内。

④ 指挥器喘振故障

预警的条件：p3的E2～E8同时都在(1.47,1.93]区间内；

报警的条件和预警的条件完全相同。

由上述结果可以看出，用气低谷出口压力偏高故障和用气高峰出口压力偏低故障的频带能量值分布基本相同，很难精准判断；指挥器喘振故障的预警与报警判断中频带能量值分布更是完全相同。单靠小波包算法无法实现研究目标，因此，需要引入多变量强关联规则完善模型。

4 高-中压燃气调压器多变量关联分析

4.1 Apriori算法理论

关联规则是一种用于探索数据趋势规律性的方法，Apriori算法[5]是用于寻找关联规则的算法之一。要归纳关联规则，首先需要建立数据实例项目集，定义项目集如式(1)。

G= {g1,g2, …,gm, …,gn}

(1)

式中G——项目集

gm——项目集G的第m个项目，m=1,2,…,n

n——项目集G中的项目总数量

G中某些项目所构成的集合为事务，定义事务如式(2)。

D= {g1,g2, …,gu, …,gw},w≤n,D⊆G

(2)

式中D——事务

gu——事务D的第u个项目，u=1,2,…,w

w——事务D中的项目总数量

项集是包含0个或多个项的集合，表示为Wn，即项集Wn为包含了n个项的集合；在事务集合中对于某个指定的项集被包含的事务数量为支持度计数；项集X和Y中所含的项在事务集中的频繁程度(百分比)表示为支持度，项集Y在包含关联规则项集X的事务中出现的频繁程度(百分比)表示为置信度，其中X和Y为项目集G中的某2个项集，且X∩Y=∅。 分别记min_sup和min_conf为最小支持度与最小置信度，即用户所能接受关联结果的程度；支持度不小于最小支持度阈值的所有项集表示为频繁项集[6]。

支持度表示规则的有用性，而置信度表示规则的确定性。关联规则挖掘旨在发现所有高于用户指定的最小支持度min_sup和最小置信度min_conf的强关联规则。Apriori算法的主要思想是逐层迭代，通过连接步与剪枝步产生频繁项集进而产生关联规则[7]。

4.2 关联规则求解

由表1变量类型可以看出，在这8种变量中，有3种变量是开关量，剩下的5种变量为模拟量，由于开关量用0和1表示关和开，不满足关联分析的条件，因此，关联规则研究采用出口压力p2、负载压力p3、支路流速v和阀位相对开度K2这4个模拟量作为研究对象，应用Apriori算法来计算多变量间相关系数与典型故障的强关联规则。

4.2.1相关系数求解

在求解关联规则前首先求出原始数据的相关系数。有学者研究表明[8]：出口压力p2与工况流速v、工况流速v与阀位相对开度K2、出口压力p2与负载压力p3这3组变量存在一定相关性，因此，可采用皮尔逊(Pearson)相关系数法分别计算出这3组变量的相关系数。为方便表达，x和y均代表p2、p3、v和K2这4个变量中的某1个变量，计算公式见式(3)。表2中9种数据类型的147组原始数据经过计算得到441个相关系数。

(3)

式中ρ(x,y)——变量x和y的相关系数

Cov(x,y)——变量x和y的协方差

σ(x)——变量x的标准差

σ(y)——变量y的标准差

4.2.2事务数据转换

为了便于Apriori算法程序后续进行读取和处理，对相关系数和数据类型进行符号化处理，进而转换为事务数据：任意变量x和y的相关系数ρ(x,y)绝对值的取值范围为[0,1]，用|ρ(x,y)|来表示，|ρ(x,y)|越大，相关程度越高，反之，则相关程度越低。将相关系数绝对值以0.05为单位长度划分成20个单位区间，并对单位区间进行符号化处理，相关系数符号见表3。例如，数据中|ρ(p2,v)|为0.03，则该数值所对应表3中的符号为A1。再把数据类型进行符号化处理，见表4。

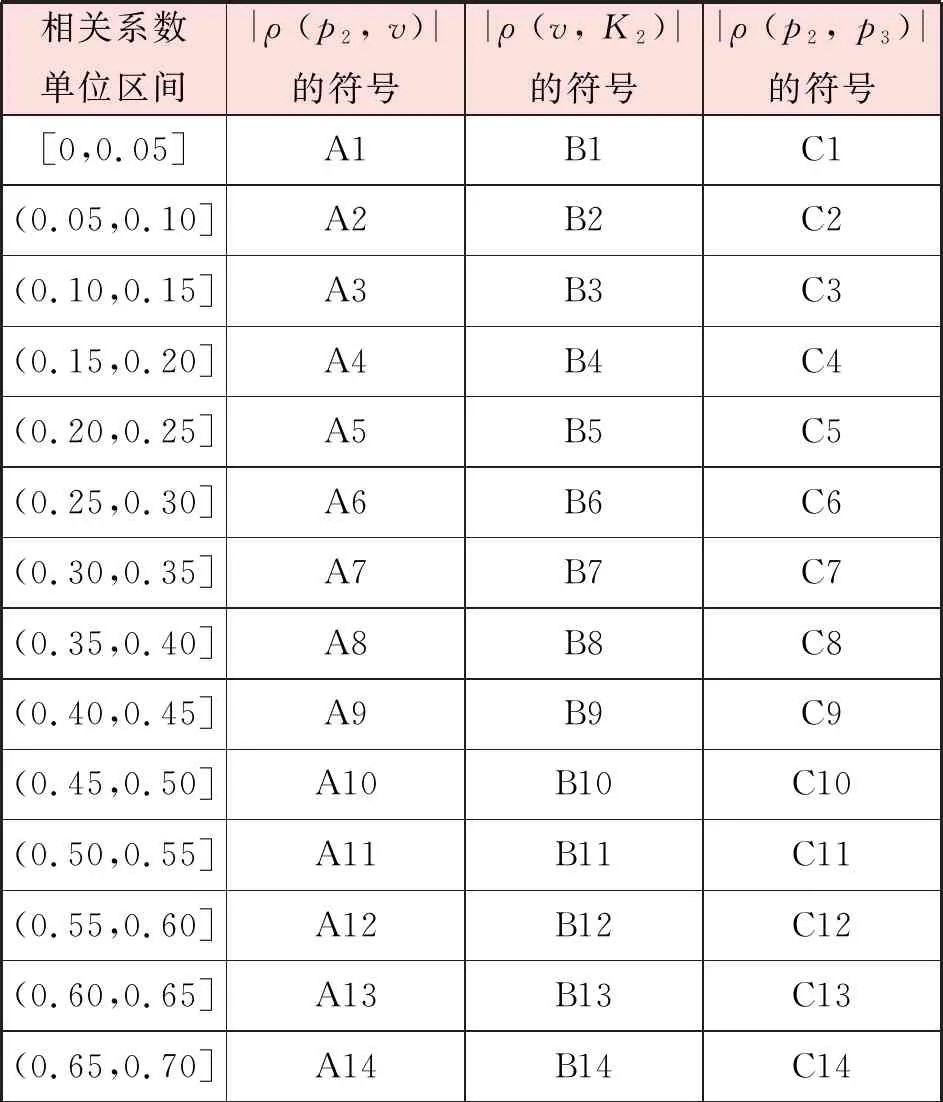
表3 相关系数符号

续表3

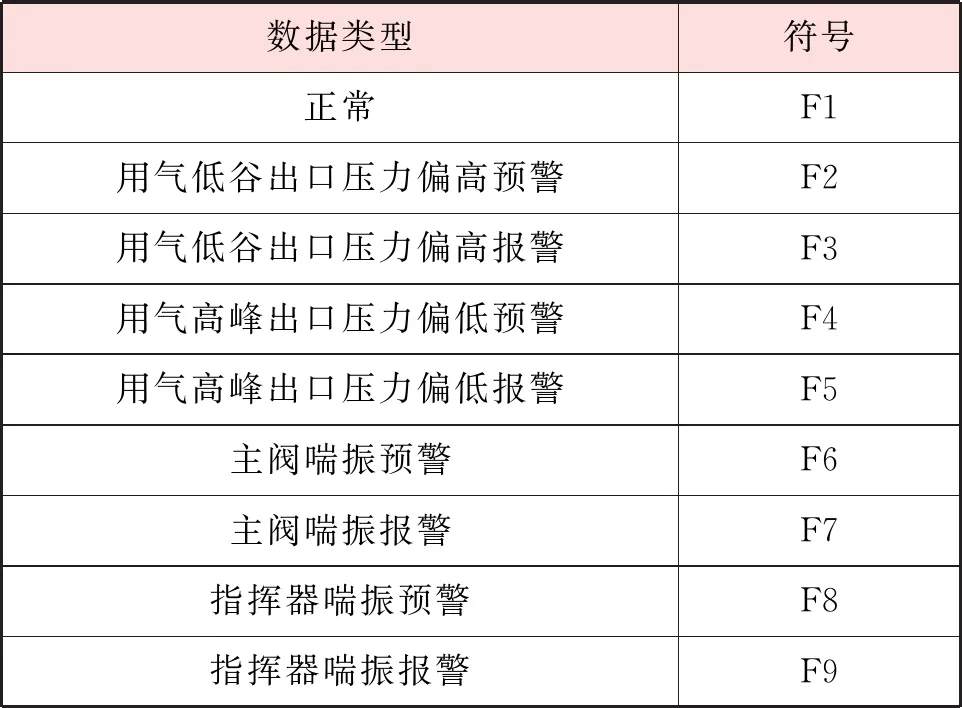
表4 数据类型符号

至此，441个相关系数及其对应的数据类型都能依据表3和表4用符号表示，从而全部转换成441个事务数据。基于147组数据，可以得到147条事务数据记录，挑选部分事务数据记录见表5。以序号2为例进行说明：当|ρ(p2,v)|=0.14，|ρ(v,K2)|=0.65，|ρ(p2,p3)|=0.43时，调压器用气低谷出口压力偏高故障级别为预警，转换成事务数据记录为：A3，B13，C9，F2。

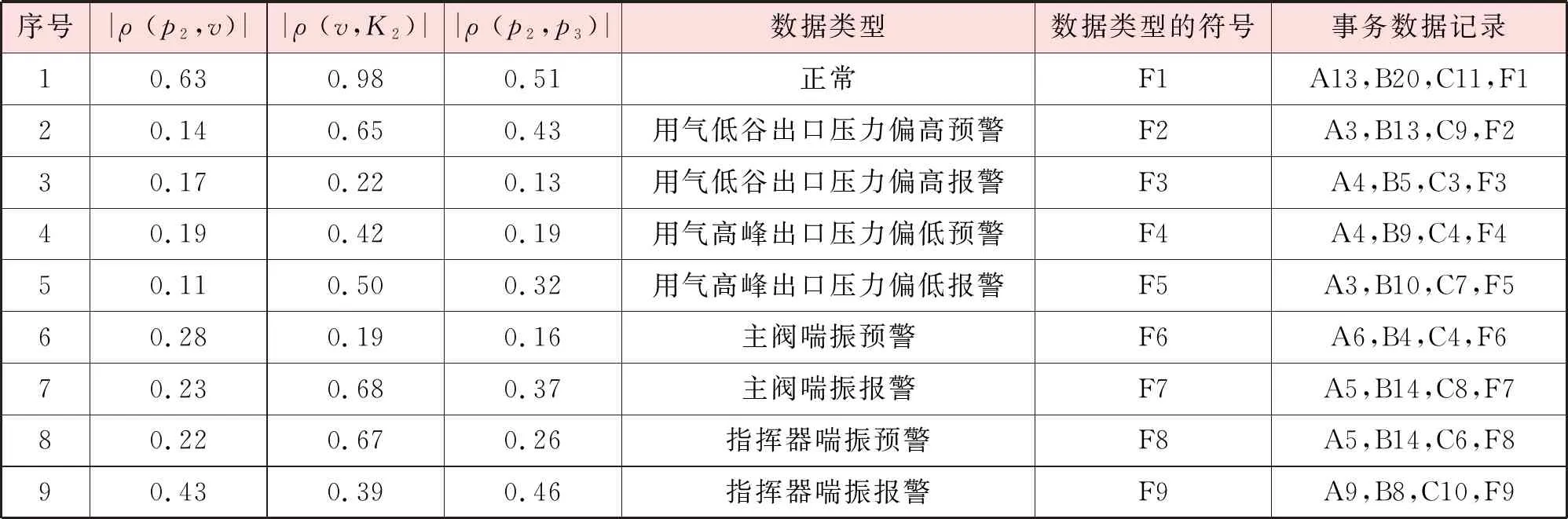
表5 部分事务数据记录

4.2.3应用Apriori算法求得强关联规则

将147条事务数据记录输入到用MATLAB语言编写的Apriori算法程序中，得到294条调压器多变量在不同故障类型下的关联规则。最小支持度和最小置信度直接影响关联规则的生成，经过反复实验对比后，本研究设定最小支持度为30%，最小置信度为50%。根据计算结果，本研究所需的具有实际意义的强关联规则为满足最小支持度与最小置信度的关联规则，经筛选后得到的高-中压调压器多变量强关联规则见表6。

表6 高-中压调压器多变量强关联规则

对表6中的强关联规则进行说明：强关联规则前件表示事件发生的条件，强关联规则后件表示事件发生的结果。以表6中第①条强关联规则为例，强关联规则前件“A1，A2，A3，A4，A5，A6，A7，A8，A9，A10，A11，A12”对照表3，其表达的物理意义为：|ρ(p2,v)|在[0,0.6]范围内；强关联规则后件“F2”对照表4，表达的物理意义为：用气低谷出口压力偏高预警。因此，第①条强关联规则为：当|ρ(p2,v)|在[0,0.6]范围内时，调压器用气低谷出口压力偏高故障级别为预警，故障级别为预警表示调压器极有可能发生故障。其他强关联规则表示的含义以此类推。

5 燃气调压器故障诊断与预警模型

以采用小波包算法对调压器出口压力及负载压力进行分解得到的频带能量值作为基础判据，以Apriori算法求解出的强关联规则作为关键判据，建立高-中压燃气调压器故障诊断与预警模型。

5.1 用气低谷出口压力偏高故障模型

用气低谷出口压力偏高故障模型见式(4)～(7)。

p2:E1∈(1.62,1.85]

(4)

|ρ(p2,v)|∈[0,0.6]

(5)

p2:E1∈(1.85, +∞)

(6)

|ρ(p2,v)|∈[0,0.5]

(7)

预警的条件：同时满足式(4)和式(5)；

报警的条件：同时满足式(6)和式(7)。

5.2 用气高峰出口压力偏低故障模型

用气高峰出口压力偏低故障模型见式(5)、(8)～(10)。

p2:E1∈(1.62,1.8]

(8)

p2:E1∈(1.8, +∞)

(9)

|ρ(p2,v)|∈[0,0.45]

(10)

预警的条件：同时满足式(5)和式(8)；

报警的条件：同时满足式(9)和式(10)。

5.3 主阀喘振故障模型

主阀喘振故障模型见式(11) ～ (15)。

p2:Ei (i=2～8)∈(0.52, 0.86]

(11)

p3:Ei (i=2～8)∈(0.4,0.95]

(12)

|ρ(v,K2)|∈[0.56,1]

(13)

p2:Ei (i=2～8)∈(0.86, +∞)

(14)

|ρ(v,K2)|∈[0.66,1]

(15)

预警的条件：同时满足式(11) ～ (13)；

报警的条件：同时满足式(12)、(14)、(15)。

5.4 指挥器喘振故障模型

指挥器喘振故障模型见式(16) ～ (18)。

p3:Ei (i=2～8)∈(1.47,1.93]

(16)

|ρ(p2,p3)|∈[0.51,1]

(17)

|ρ(p2,p3)|∈[0.56,1]

(18)

预警的条件：同时满足式(16)和式(17)；

报警的条件：同时满足式(16)和式(18)。

从上述数学模型中可以看出，在小波包频带能量值判据的基础上，加入多变量相关系数与典型故障的强关联规则后便能有效区分各类故障以及预警与报警，弥补了单靠小波包算法无法精确区分部分类型故障以及无法有效判断预警与报警的缺陷，提升了模型的精准度。

6 模型验证

首先选取某燃气公司检修中心整理的2020年调压器检修记录中专家技师判定的7组故障历史数据和14组异常历史数据，共21组数据。之后把这21组数据经小波包与Apriori算法分析后代入到高-中压燃气调压器故障诊断与预警模型中，该模型对7组故障数据进行了报警判断，报警所判断的故障与专家技师给出的判定完全吻合。14组异常数据模型判断为预警，然后经检修中心技师确认，该14组异常数据所对应的14个调压器经检修均发现不同程度零部件老化破损，如不及时更换零部件，调压器将会发生故障。

因此，此次验证证明了该模型具备对高-中压燃气调压器进行故障诊断及预警的能力。

7 结论

① 采用小波包算法对调压器出口压力及负载压力进行分解得到的频带能量值可作为基础判据。

② Apriori算法得出的多变量相关系数与故障类型之间的强关联规则可以作为关键判据，提升高-中压燃气调压器故障诊断与预警模型的精准度。

③ 应用小波包算法和Apriori算法相结合的方法建立的高-中压燃气调压器故障诊断与预警模型经实例验证可行。