机载SAR 天线高精度指向稳定平台设计

周 鲁, 张 乐, 赵桂军, 曹培培, 陈 琦

(上海无线电设备研究所,上海 201109)

0 引言

合成孔径雷达(SAR)具备全天候、全天时和远距离成像的特点,在资源勘察、灾害预警、环境监测以及军事侦察等领域内得到了广泛的应用。机载合成孔径雷达的天线稳定平台作为隔离机体扰动、稳定天线波束指向的运动补偿执行机构,其稳定精度直接影响SAR 成像的质量与分辨率。在早期,运动补偿直接采用飞机主惯导的导航数据。但是由于飞机的主惯导是按照飞机导航的要求设计的,而且距离天线的相位中心较远,所以主惯导的导航数据无法完全真实地反映天线的运动状态。后来高分辨率机载SAR 系统中又增添了专门用于测量天线相位中心运动误差的惯性测量单元(inertial measurement unit,IMU)。但是惯性测量单元的长期累积误差会随着时间而发散,这将严重影响SAR 的分辨率,甚至导致无法成像。为了解决以上问题,目前一般采用的是基于卫星定位和惯性测量单元的组合导航解算运动补偿方案[1-3]。本文基于组合导航的运动补偿方式,设计稳定平台控制系统。

1 SAR 天线稳定平台

1.1 稳定平台组成

采用滚转外框架、俯仰内框架式的万向支架结构稳定平台作为天线的机构载体,在飞行过程中确保SAR 天线隔离载机扰动,维持指向稳定,并设置天线的相关位置摆动幅度,以满足不同载机空间需求。稳定平台组成框图如图1所示。

图1 SAR 天线稳定平台的组成框图

稳定平台主要由组合导航系统、角位置传感器、伺服机构(包括框架机械机构和直流力矩电机等)、数字控制器和脉冲宽度调制(pulse width modulation,PWM)驱动器构成。天线的方位角φy和俯仰角φz由角位置传感器测量,载体扰动角速度(ωx,ωy,ωz)和姿态角(θx,θy,θz)由组合导航系统测量。上述信号经过信号变换、滤波后,送入数字控制器,最后给出天线方位与俯仰控制指令信号u y和u z来驱动伺服机构,控制天线转动,从而实现隔离载体扰动的功能,保证天线空间指向的稳定。

1.2 稳定平台控制模型

从稳定平台组成可以看出,为了实现天线的高精度稳定指向控制,控制模型必须要精确。以稳定平台控制系统的方位通道为例,伺服机构由直流力矩电机和相关负载组成,控制对象模型的结构框图如图2 所示。其中,u y为电机控制电压,L为电机电感,Ra为电机电枢电阻,Ia为电枢电流,Km为力矩系数,MR为电机或外在因素的扰动力矩,Ma为电机力矩,J为负载等效到电机轴的转动惯量,Ke为反电势系数,θ·y为机构方位通道角速度,θy为机构方位通道角度。

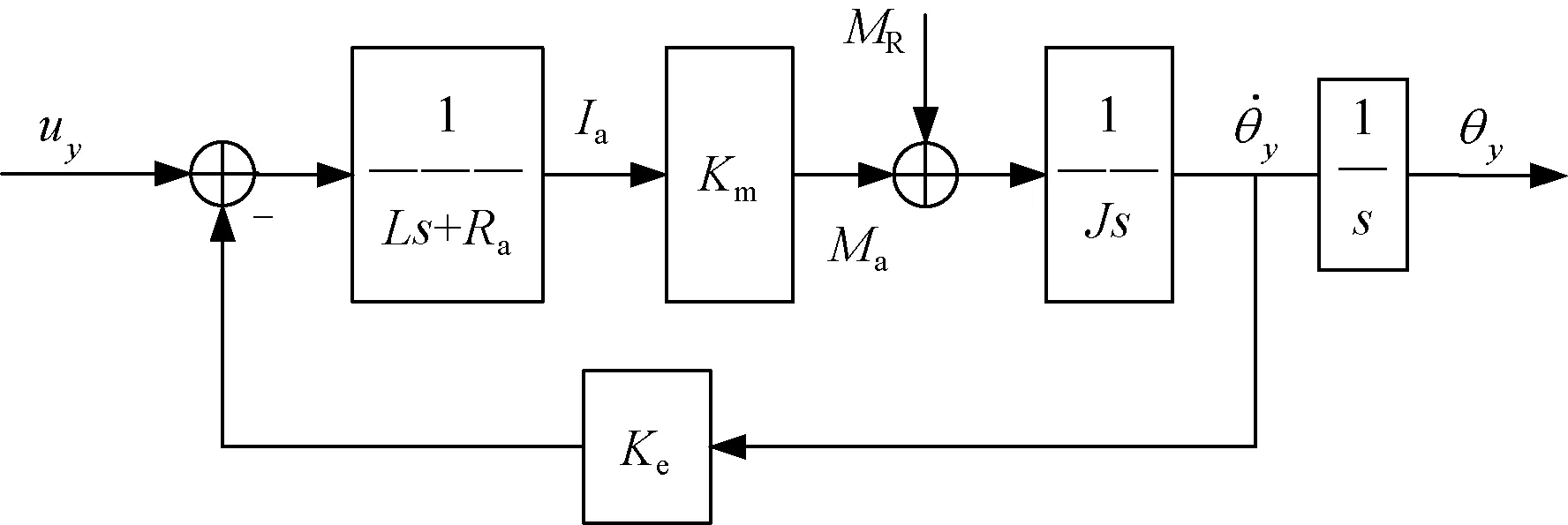
图2 稳定平台方位通道的控制对象模型

电机选定后,按照图2模型,控制回路的传递函数为

计算得到的模型中,负载的转动惯量有一定的误差,可通过对实物进行扫频拟合,来修正得到控制对象的精确数学模型。

1.3 控制回路设计

获取控制对象模型后,按照图1的稳定平台组成框图进行回路设计,其中组合导航系统和角位置传感器的选取按照系统精度要求进行论证,不再详细展开。载体运动状态利用组合导航系统测量出的三轴角速度和角度信息,通过坐标变换和滤波获得,该部分可以看作是前馈补偿。在控制系统中,前馈补偿实际上就是采用开环控制方式去补偿可量测的扰动信号。前馈补偿并不改变反馈控制系统的特性,其补偿效果主要取决于前馈补偿装置的性能,在组合导航系统的安装和解算算法实现中,不影响主控通道的控制回路设计。以下重点对控制回路前向通道和角位置传感器反馈通道进行设计。

针对图2 的控制对象模型进行控制回路设计,采用PWM 功率驱动和滤波,限幅为±24 V,通过输出直接控制电机的转动。原理框图如图3所示。

图3 稳定平台控制回路的原理框图

图3中,ϕ为控制信号,Δϕ为误差信号,G y为控制器回路校正传递函数,KPWM为脉冲宽度调制功率放大增益,u y为电机驱动电压,GM为控制对象模型的传递函数,Ωm为机构角速度。

采用FPGA(V5-95T)为处理芯片实现数字信号处理,采样频率为2 k Hz,PWM 功率驱动开关频率为20 k Hz,滤波带宽为1 k Hz,增益为1。

因电机时间常数较大,控制器设计中采用一个零点来补偿,相应要补一个极点来平衡。为抑制机构谐振及噪声影响,需针对性地设置极点。考虑到该控制回路的带宽要求不小于10 Hz且机构谐振频率为160 Hz,在小于160 Hz处选取一个实极点,对应时常数为0.001 s。为使满足指标要求的系统更容易实现,再设置1个零点和1个极点来进行性能调整。得到回路校正传递函数为

式中:t1,t2,TD为控制器待定参数。

使用Simulink 工具进行回路设计,应用“Compensators Design” 工 具 和 “Signal Constraint”模块对回路进行综合分析和优化,得到控制器参数:K y=120,t1=0.004,t2=0.01,TD=0.002。

2 稳定平台优化设计与试验验证

在进行线性设计时,往往会忽略模型中的限幅特性、死区特性等非线性因素。但在工程实际中,限幅特性限定了前向通道的增益,死区特性取决于机电传动装置的不灵敏区,直接影响伺服系统的精度指标,因此这些因素必须加以考虑[4-5]。本文针对实际工程中遇到的死区问题和机构非线性问题,从死区增益控制和自适应积分补偿控制两个方面对控制系统进行了优化设计。

2.1 死区增益控制

假设组合导航系统解算的精度满足系统精度0.1°的要求,针对死区和饱和特性对伺服系统精度的影响,对回路的控制器进行优化设计。机电传动装置不灵敏区主要是由机电传动装置的启动电压,即死区的非线性因素造成,由工程经验和机电传动装置力矩特性确定启动电压utp小于4 V。将不灵敏区造成的误差折算到Δϕ输入端,记为Δϕsq,计算得出控制电路的前向通道放大系数K y,表达式为

根据式(3),若伺服控制平台要求位置精度为0.1°,则K y应大于266。

2.2 自适应积分补偿控制

考虑死区的非线性因素,系统精度在死区增益控制方法中可以通过增大增益来保证,而电路的饱和特性会限制回路的增益,如果一味地增加回路增益,系统的稳定性就会受到威胁。

在实际控制过程中,可以通过实时检测位置误差和增加自适应积分补偿前馈控制器等措施,来修正控制指令,提高系统性能。原理框图如图4所示。

图4 自适应积分补偿控制回路原理框图

式中:ϕe0为指令初始值;D为修正步长。

采用Matlab中的Simulink仿真软件对优化控制算法进行仿真,采用自适应积分补偿控制算法前后,系统响应的仿真曲线如图5所示。优化前误差为0.17°,优化后误差为0.03°,由此可见该方法可以有效提高系统控制精度。

图5 控制算法优化前后响应曲线

2.3 试验验证

为验证稳定平台控制系统的性能,进行了挂机飞行试验。飞机按照指定航线飞行,飞行过程中天线方位角测试曲线如图6所示。经过数据分析,方位角均方差为0.051 4°,满足系统指标0.1°的要求。

图6 挂飞试验天线方位角测试曲线

3 结论

本文设计了一种基于组合导航运动补偿方式的SAR 成像系统稳定平台,并进行了数学建模。为了解决工程实际中存在的死区和机构非线性等问题,以方位通道为例进行控制算法的设计优化。采用死区增益控制和自适应积分补偿控制的方法,既保证了系统的稳定性又提高了系统的稳定指向精度。仿真试验和外场挂飞试验结果表明:系统对载体的扰动可以较快地作出响应,角位置误差小于0.1°,指向精度达到工程预期要求;实现了隔离机体姿态变化对波束指向影响的目标,保证了天线姿态和波束指向的稳定性,为在无人机等载体上实现高分辨率SAR 成像提供了保障。