基于GM-PHD 的低可观测编队目标跟踪方法

张 杨，顾祥岐

（海军航空大学，山东 烟台 264001）

0 引言

19 世纪50 年代至今，目标跟踪理念基本框架已经完善，相关技术也已快速发展为热门的研究方向，并被广泛应用到交通、军事、金融等领域［1-4］。目标跟踪技术在发展过程中，研究对象是从单目标到多目标的，编队目标是多目标的一种特殊形式，具有空间距离较近且以相似状态运动的特点，这种特殊性使得编队目标生成的探测点迹分布多且密集，导致跟踪难度很大，因此，针对编队目标的目标跟踪技术［5-8］受到了国内外学者们的广泛关注。

在实际编队作战场景中，当目标本身具有一定的隐身能力或受到强杂波、天气等外部因素干扰的时候，都会因目标低可观测导致传感器检测目标的概率减小，漏检、虚警等问题频繁出现，稳定跟踪目标的难度变大，严重影响跟踪算法的性能。因此，低可观测情况下的编队目标跟踪技术研究已成为工程应用领域中亟待解决的问题，受到了国内外专家学者们的广泛关注，并取得了一定的成果。

针对低可观测情况下编队目标的跟踪问题，文献［9］提出了一种基于Kenefic（N，M）扫描分支滤波器的低可观测目标跟踪算法，该算法是以延长跟踪无关轨迹的时间和概率比检验为主要手段，实现对目标的稳定跟踪；文献［10］提出先利用MHT 算法对目标进行滤波估计，再结合顺序似然比检验方法找出最优估计状态，最终得到目标轨迹；文献［11］提出了一种结合PDA 和最大似然估计的目标跟踪算法， 该算法以杂波中的Cramer-Rao 下界为量化估计标准，能够较为有效地跟踪低可观测情况下的目标；文献［12］提出利用GM-PHD 滤波算法，结合聚类方法得到编队质心的状态，以质心轨迹反映编队整体运动轨迹；文献［13］提出在GM-PHD 滤波框架下，通过对前一时刻权值过大的高斯项进行修正，以保证当前时刻高斯项的权值稳定，大大提高了跟踪结果的准确性；文献［14］设计了一种GM-PHD 平滑滤波器，其思想是在PHD 滤波过程中加入前向递推和后向平滑两个步骤，有效提升了算法的跟踪性能；文献［15］提出在目标状态提取过程中，充分利用高斯项的权值和存在概率，从目标后验强度中找出漏检目标的状态估计值，消除低可观测对跟踪结果的影响，使得算法具有较好的鲁棒性。然而，这些算法适用可观测情况的检测概率只是相对较低（检测概率最小的仅为0.5）。而且，鉴于编队目标的特殊性，当检测概率特别低时，可能出现闪烁甚至是断续的现象，现有方法跟踪的状态估计结果会出现较大偏差，跟踪性能很差。

为适应可观测性极低的情况，本文利用编队目标的特点，在GM-PHD 滤波框架下，提出了一种结合JS 散度［16，17］和密度聚类［18］的编队目标跟踪方法，并通过仿真实验验证了算法的有效性。

1 问题模型

2 算法流程

实际作战中，编队目标所处环境大部分都是可观测性能极差的，雷达等预警探测装置获取目标信息是非常困难的，因此，跟踪目标的困难程度也大，大量真实目标被遗漏。经实验验证可知，PHD 滤波算法在此环境下，出现大量真实目标被遗漏的原因是，真实目标因漏检导致其权值变小，进而在高斯项修剪融合过程中真实目标对应的高斯项容易被剪掉，这样真实目标就会被遗漏。

本文提出了基于GM-PHD 滤波算法的编队目标跟踪方法，该方法是将先进行GM-PHD 滤波算法的预测与更新过程，再对更新的高斯项进行修剪和融合，在修剪融合过程中，需要保留剪掉的所有高斯项，并将它们在当前模型下外推状态一次，然后利用JS 散度判断这些状态值与下一时刻状态值之间的相似程度。如果判断结果为相似，则真实目标已被遗漏，将被遗漏目标高斯项的状态值放到状态估计集合中；如果判断结果为不相似，则继续外推这些高斯项的状态值。最后，结合密度聚类方法对估计状态集合进行分类，类数就是编队数量。

2.1 预测与更新

2.2 状态外推

鉴于低可观测环境下真实目标因被遗漏使得其对应高斯项权值变小，所以修剪掉的高斯项中极有可能包含了真实目标。为避免这种情况发生，对所有被剪掉高斯项的状态进行外推，判断确实没有真实目标后再去除。

根据式（3）和式（5），可设k-1 时刻修剪融合过程中被剪掉高斯项的状态估计为

2.3 相似性判断

通常，高斯项外推次数不会超过3 次，因为如果一个高斯项3 次外推后仍然不是真实目标，那么就可以判断为虚假信息，这种情况下的错误率已经很低，不会影响目标跟踪的稳定性。

2.4 编队分类

考虑到状态估计集合中既要包含滤波更新修剪融合后的估计状态值，又要包含状态外推后经相似性判断筛选出的状态值，这样一来状态估计集合中目标数量过多，影响跟踪结果的准确性。因此，利用编队目标生成探测点迹多而密的特点，结合密度聚类方法对编队整体进行有效跟踪。这里用到的密度聚类方法是DBSCAN 算法，该算法是一种典型密度聚类算法，它能够利用观测区域内点迹的密集程度来找到编队的位置，不受编队结构形状影响。

该过程的具体步骤如下：

第3 步，找出每个编队目标状态估计值集合中权值最大的状态估计值，这个状态估计值就是该时刻的对应编队目标的状态估计值。

3 仿真实验与结果分析

3.1 仿真场景设置

3.2 仿真结果分析

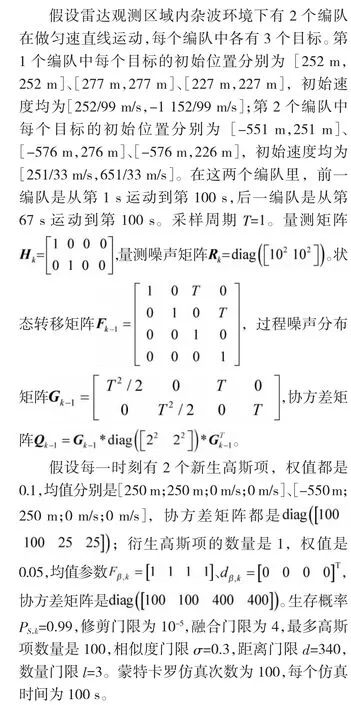
本文算法主要与GM-PHD 算法进行对比。图1是检测概率PD，k=0.5、杂波数量均值λ=10 时的目标真实轨迹图。图中，黑色直线为编队目标的真实轨迹，黑色点迹为量测数据。

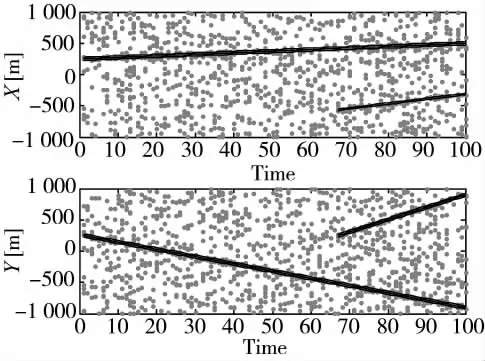
图1 目标真实轨迹图

图2 和图3 是PD，k=0.5、λ=10 时两种算法的单次仿真状态估计图。图中，黑色直线表示编队目标的真实轨迹，黑色圆圈表示目标的估计状态值。对比图2 和图3，可以明显看出本文算法的跟踪结果更准确，目标不会因检测概率较低而被遗漏，估计状态信息十分完整。

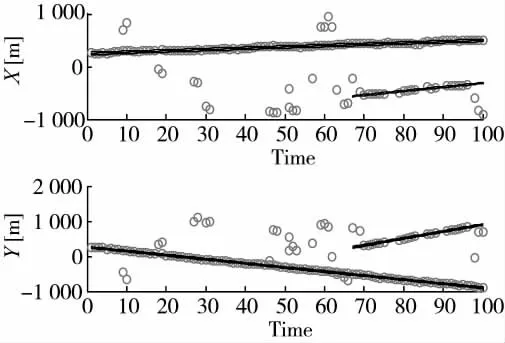
图2 GM-PHD 算法的单次仿真状态估计图

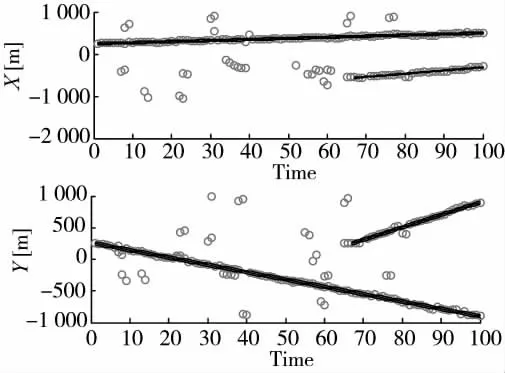
图3 本文算法的单次仿真状态估计图

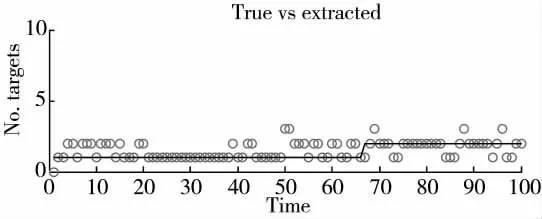
图4 GM-PHD 算法的目标个数估计图

图5 本文算法的目标个数估计图

对比图2～图5 可知，PD，k=0.5、λ=10 时，综合单次仿真状态估计结果和目标数量估计结果来看，本文算法的跟踪性能更好。

图6～图9 分别为PD，k=0.7、λ=10 和PD，k=0.3、λ=10 时两种算法的目标数量估计图。对比图4～图9 可知，检测概率不变时，本文算法的跟踪性能更好；若检测概率在减小，本文算法性能下滑更小。当检测概率极小时，本文算法依然能够很好地跟踪目标，性能依然很好，跟踪精度也很高。

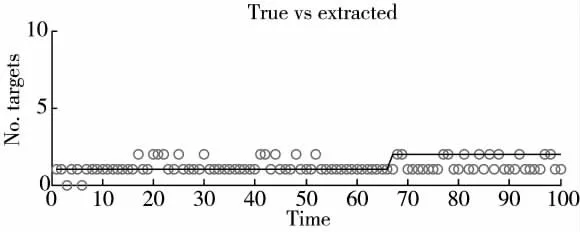
图6 GM-PHD 算法的目标个数估计图

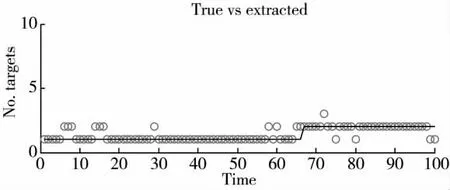
图7 本文算法的目标个数估计图

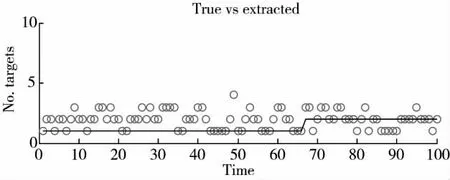
图8 GM-PHD 算法的目标个数估计图

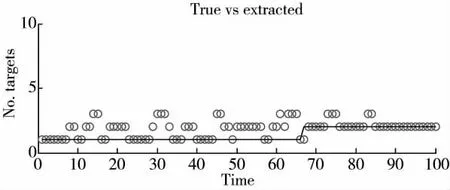
图9 本文算法的目标个数估计图

表1 是杂波数量均值λ=10、检测概率分别是PD，k=0.7、0.5、0.3 时，两种算法的平均最优子模式分配（OSPA）距离［20］表。如表1 所示，检测概率与两种算法的平均OSPA 距离差值是成反比的，本文算法的跟踪性能一直比GM-PHD 滤波算法好。

表1 平均OSPA 距离表

4 结论

本文为解决可观测性较低情况下存在的多编队目标跟踪问题，提出了一种以GM-PHD 滤波算法为基本框架，结合JS 散度和密度聚类的编队目标跟踪方法，该方法的优点有3 个：1）结合JS 散度判断修剪融合过程修剪掉所有高斯项的外推状态值与下一时刻状态估计值间的相似性，保证了真实目标不被遗漏，提升了算法的跟踪性能。2）利用编队目标的特点，结合密度聚类算法分类编队，避免因状态估计集合中估计值过，影响跟踪结果准确性的情况发生，有效跟踪了编队目标的整体运动状态。3）虽然本文方法的复杂程度稍高，但是，根据仿真实验结果表明，本文算法的稳定性和准确性明显高于GM-PHD 滤波算法，能够在可观测性极低、强杂波环境下依然保持较好的跟踪性能，具有良好的工程应用前景。