考虑交流侧特征谐波的电网换相换流器小信号建模*

殷作洋，康蓝心，陈 秘，舒莘珂

（国网四川省电力公司广安供电公司，四川 广安 638000）

0 引言

随着电力电子技术的快速发展，电网换相换流器（Line Commutated Converter，LCC）被广泛应用于车辆、飞机、船舶、雷达站供电等军用电力系统领域［1-2］。例如，基于电网换相换流器型高压直流输电（Line Commutated Converter Based High Voltage Direct Current，LCC-HVDC）系统在远距离输电应用场合发挥着不可替代的作用，可应用于为军用雷达站、边防哨所、军事基地等重要军事设施进行远距离供电。

围绕LCC-HVDC 的拓扑结构、控制策略、稳态运行极限、换相失败等问题，国内外学者已取得了一系列卓有成效的成果［3-6］。考虑控制系统对LCC- HVDC 系统运行特性的影响，目前已成为分析研究LCC-HVDC 系统的学术热点之一。文献［7-8］建立了单端LCC 逆变站的小信号模型，分析了锁相环（Phase Locked Loop，PLL）以及定直流电压控制器参数对系统小信号稳定性的影响，结果表明在弱交流系统工况下，增大PLL 控制器参数将导致系统小信号失稳；文献［9］建立了包含静止同步补偿器（Static Synchronous Compensator，STATCOM） 的单端LCC 小信号模型，分析了PLL、LCC-HVDC 与STATCOM 控制系统参数对整个系统的小信号稳定性与动态性能的影响，并得到不同控制系统参数的可行域。文献［10］在文献［9］的基础之上，针对弱交流系统工况，提出了一种附加阻尼协调控制方法，用于增强系统的小信号稳定性。上述文献所建立的LCC 小信号模型，仅考虑了LCC 逆变站，其建模过程中直流侧模型采用直流电流源替代，并未考虑LCC 整流站及直流线路的动态特性影响；且建立的小信号模型仅考虑了交流侧基频分量，没有考虑LCC 换流器交流侧的特征谐波分量。

为了充分研究和分析不同运行工况及控制系统对LCC-HVDC 系统小信号稳定性的影响，需建立能够准确反映LCC-HVDC 系统动态特性的小信号模型。本文采用考虑LCC 换流器交直流侧变换关系的开关函数模型，建立包含LCC 整流站、LCC 逆变站以及直流线路模型的双端LCC-HVDC 小信号模型，并通过与PSCAD/EMTDC 详细电磁暂态LCC-HVDC 模型对比，验证模型的准确性；在此基础之上，对比考虑交流侧特征谐波分量和仅考虑基频分量的两种不同小信号模型，分析其在小信号稳定性方面的差异。

1 LCC-HVDC 小信号建模

1.1 LCC-HVDC 拓扑结构

典型的双端LCC-HVDC 直流输电系统示意图如图1 所示，根据图1 可将双端LCC-HVDC 系统的小信号建模划分为整流站模型、逆变站模型及直流线路模型。以下将针对上述3 部分模型具体阐述小信号建模过程。

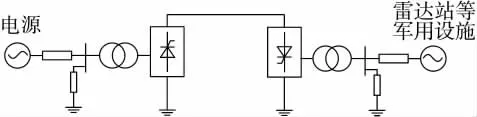
图1 LCC-HVDC 示意图

1.2 LCC 整流站数学模型

LCC 整流站模型示意图如图2 所示，图2（a）为LCC 整流站等效电路，其中，Idcr，Udcr为LCC 整流侧直流电压和直流电流，utr，usr分别为整流侧公共连接点（Point of Common Coupling，PCC）电压和交流系统等值电动势，icr，isr分别为LCC 整流站阀侧和交流侧电流，kr和Ltr为LCC 整流站换流变压器的变比和等值漏感，Rsr，Lsr分别为整流侧交流系统的等值电阻和等值电感。

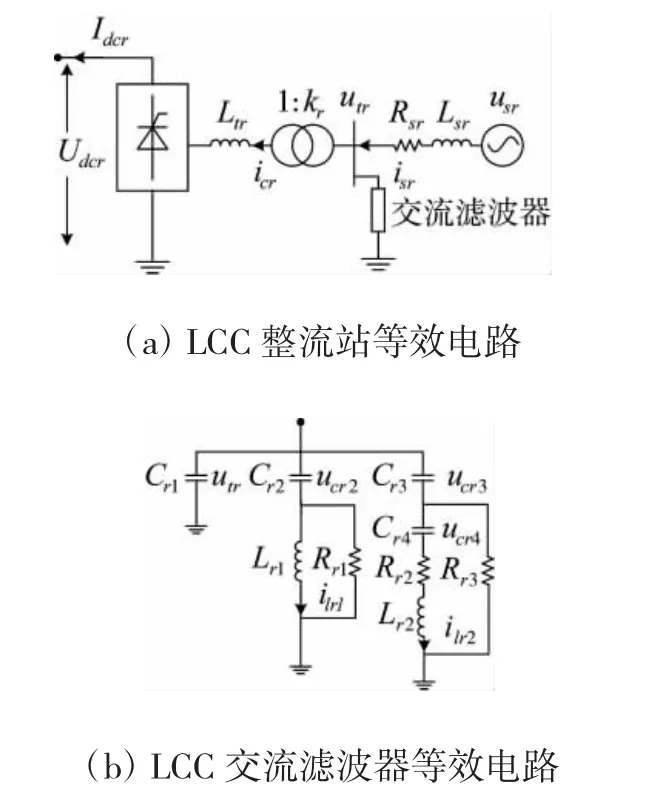
图2 LCC 整流站示意图

仅考虑LCC 整流站的基频分量，基于对开关函数的傅里叶分解［11］，基频下LCC 整流站的阀侧电流和整流侧直流电压可表示为：

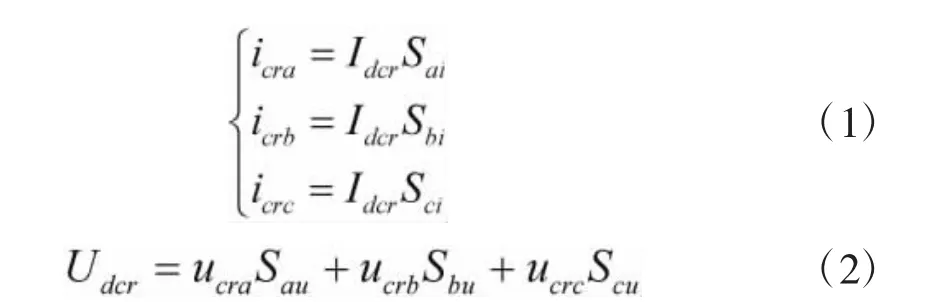
其中，Sai～Sci代表直流电流与交流三相电流之间的开关函数，Sau～Scu代表交流三相电压与直流电压之间的开关函数，可表示为：

式中，Utr为交流母线电压有效值，αr为整流侧控制触发角，φr为LCC 整流侧功率因素角，可表示为：

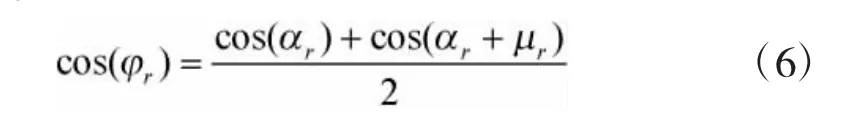
在dq 坐标系下LCC 整流站阀侧电流的dq 分量icdr和icqr可表示为：

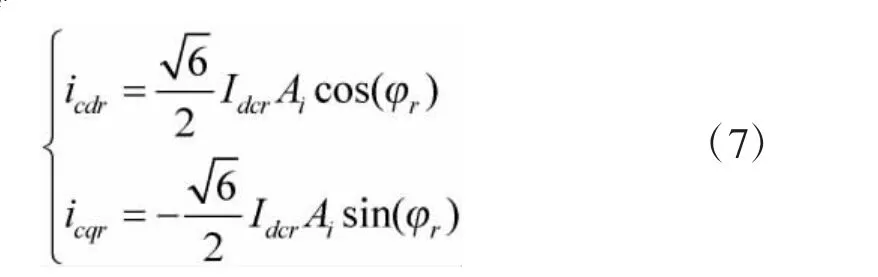
图2（b）为整流侧LCC 交流滤波器的等效电路图，其拓扑结构与CIGRE 标准测试模型［12］一致，其中Cr1～Cr4、Lr1～Lr2和Rr1～Rr3分别为LCC 交流滤波器的等值电容、等值电感和等值电阻；ucr2～ucr4和ilr1～ilr2分别为交流滤波器的电容电压和电感电流。根据图2（a）和图2（b）可建立dq 坐标系下LCC 整流站交流侧电压、电流微分方程组：

对于CIGRE 标准测试模型，其整流侧采用定直流电流控制。图3 给出了LCC 整流站的基本控制系统结构框图。

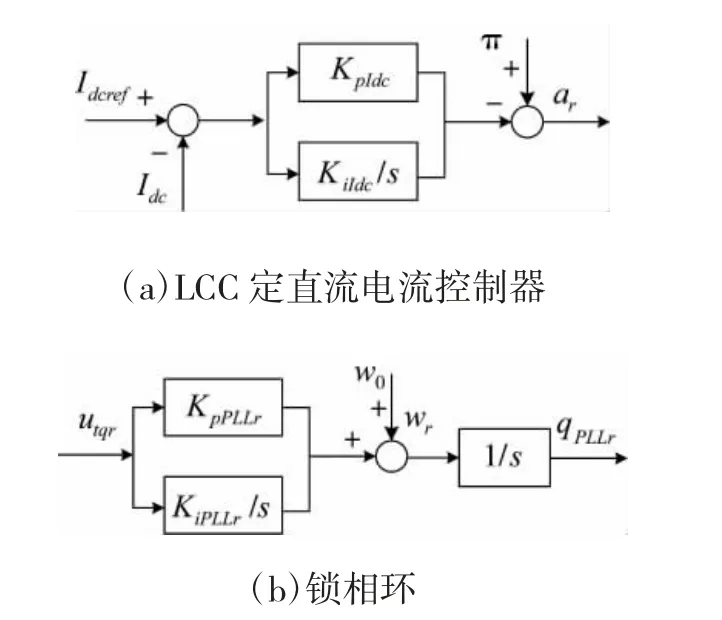
图3 LCC 整流站控制系统结构框图

如图3（a）所示为LCC 定直流电流控制器结构框图，图中Idcref为直流电流参考值，KpIdc和KiIdc为定直流电流控制器的比例和积分增益系数。根据图3（a）可建立LCC 定直流电流控制器微分方程：

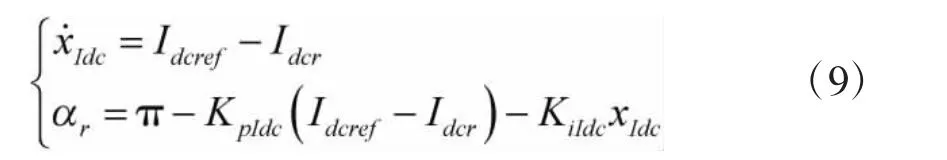
图3（b）为LCC 整流站的PLL 结构示意图，其中，ω0，ωr分别为额定电角速度和PLL 输出的电角速度，θPLLr为整流侧PLL 输出相角，KpPLLr和KiPLLr分别为PLL 比例和积分增益系数，xIdc为描述定直流电流控制环节数学模型而引入的中间变量。根据图3（b）建立PLL 微分方程如下所示。

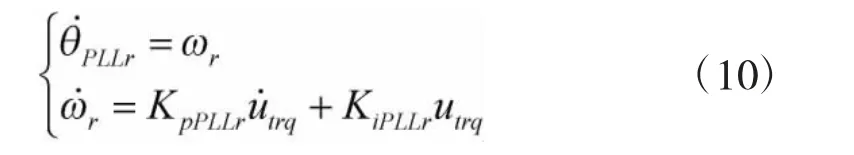
1.3 LCC 逆变站数学模型

LCC 逆变站模型示意图如下页图4 所示，图4（a）为LCC 逆变站等效电路，其中，Idci，Udci为LCC 逆变侧直流电压和直流电流，uti，usi分别为逆变侧PCC电压和交流系统等值电动势，ici，isi分别为LCC 逆变站阀侧和交流侧电流，ki和Lti为LCC 逆变站换流变压器的变比和等值漏感，Rsi，Lsi分别为逆变侧交流系统的等值电阻和等值电感。

图4 LCC 逆变站示意图

与LCC 整流站类似，在dq 坐标系下LCC 逆变站阀侧电流的dq 分量icdi和icqi可表示为：

式中，Utr为交流母线电压有效值。

图4（b）为LCC 逆变站的交流滤波器，其拓扑结构参考CIGRE 标准测试模型，其中，Ci1～Ci4、Li1～Li2和Ri1～Ri3分别为LCC 交流滤波器的等值电容、等值电感和等值电阻，uci2～uci4和ili1～ili2分别为交流滤波器的电容电压和电感电流。根据图4 可建立dq 坐标系下LCC 逆变站交流侧电压、电流微分方程组：

图5 给出了LCC 逆变站的定关断角控制的结构框图。其中，γ 和γref分别是LCC 逆变站的关断角和定关断角控制器的参考值，βi和αi分别为LCC 逆变站的超前触发角和控制触发角，Kpγ和Kiγ分别为LCC 定关断角控制器的比例和积分增益系数。

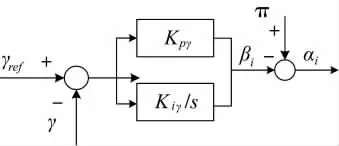
图5 LCC 定关断角控制结构示意图

根据图5 可建立LCC 定关断角控制器的微分方程：

LCC 逆变站的PLL 结构框图与图3（b）相同，对应的微分方程也一致，在这里不再赘述。

1.4 直流线路模型

下页图6 为LCC-HVDC 直流线路等效电路，其中直流线路参照CIGRE 标准测试模型采用T 型等效电路模型，其中，Rdcr和Rdci分别为整流侧和逆变侧的直流线路等值电阻，Ldcr和Ldci分别为整流侧及逆变侧包含平波电抗器和直流线路电感的等值直流电感，C 为直流线路等值电容，Udc为等值电容上的直流电压。

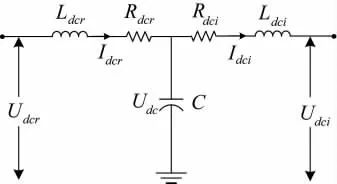
图6 LCC-HVDC 直流线路等效电路

图6 中整流侧及逆变侧直流电压Udcr和Udci可分别表示为：

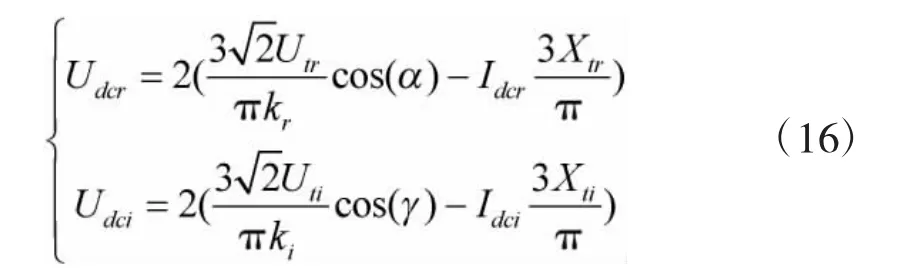
根据图6 可建立LCC-HVDC 直流侧电压、电流微分方程：

结合式（1）～式（17）共同构成了双端LCC-HVDC系统的状态空间方程，对其在平衡点处线性化处理后，可以得到对应双端LCC-HVDC 系统的小信号模型。

2 模型验证

为了验证第1 节所建立的双端LCC-HVDC 小信号模型的准确性，分别在电磁暂态仿真软件PSCAD/EMTDC 上搭建如图1 所示的双端LCCHVDC 详细电磁暂态仿真模型，在MATLAB 上建立双端LCC-HVDC 小信号模型。其中，PSCAD/MTDC仿真环境下搭建的LCC-HVDC 详细电磁暂态仿真模型，能够准确反映系统的电磁暂态过程，在相同稳定运行工况下，通过对比本文所建立的小信号模型与PSCAD/EMTDC 仿真模型的动态特性，可以验证本文所推导建立的小信号模型的准确性［7-10］。

LCC-HVDC 的模型参数如表1 所示，整流侧采用定直流电流控制，逆变侧采用定关断角控制，控制系统参数如表2 所示。

表1 LCC-HVDC 系统参数

在1.0 s 时改变LCC 整流站定直流电流控制器参考值Idcref由1.0 p.u.阶跃至1.05 p.u.，基于PSCAD/EMTDC 详细模型和MATLAB 小信号模型的整流侧和逆变侧仿真波形对比结果如下页图7 所示。

从图7 中可以看出，当LCC 整流站定直流电流控制器参考值Idcref发生阶跃扰动时，根据本文第1节所建立的小信号模型与PSCAD/EMTDC 详细模型整流侧直流电流、交流母线电压，以及逆变侧关断角和交流母线电压的动态响应特性的仿真波形动态过程一致，从而证明了本文所建立的双端LCC-HVDC 小信号模型的准确性。

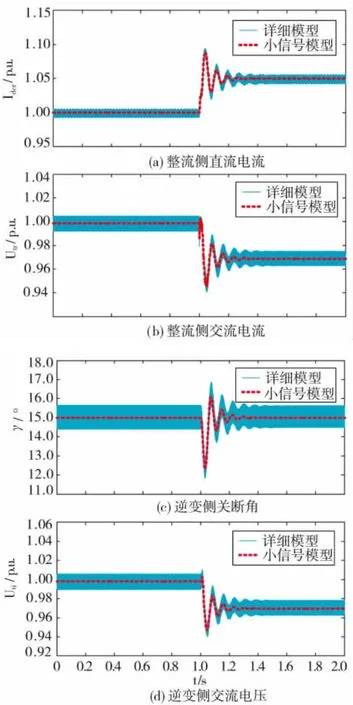
图7 直流电流设定值阶跃时LCC-HVDC 系统的动态特性

3 交流侧特征谐波分量影响分析

本文第1 节所建立的双端LCC-HVDC 小信号模型仅考虑了基频分量，而未考虑交流侧的特征谐波分量。对于12 脉动LCC 换流器，其交流侧含有12k±1（k 为正整数）次特性谐波，考虑高次谐波的幅值随谐波次数的增加而显著降低［13］，主要考虑对交流系统影响最大的11 次、13 次以及23 和25 次谐波分量。考虑特征谐波分量后，LCC 换流器的开关函数可表示为：

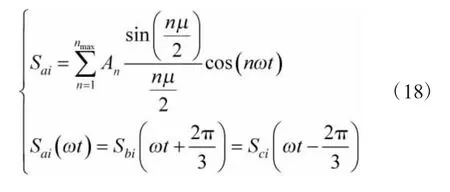
将式（18）～式（20）代入LCC 整流站和逆变站相应电压、电流表达式中，并考虑其对交流侧电压、电流式（11）的影响（修改对应的频率ω 为nω），可得到考虑交流侧特征谐波分量的双端LCC-HVDC系统的非线性方程，对其在平衡点处线性化处理后可建立考虑交流侧特征谐波分量的小信号模型。

为了对比考虑交流侧谐波分量的LCC-HVDC小信号模型与仅考虑基频分量的LCC-HVDC 小信号模型的区别，分别设置两组不同的小信号模型：

小信号模型1：考虑交流侧特征谐波分量；

小信号模型2：仅考虑交流侧基频分量。

图8 为LCC 逆变侧滤波器电流ili2的PSCAD详细模型与小信号模型1 和小信号模型2 的对比波形。从图中可知，由于存在交流侧特征谐波分量，LCC 逆变站交流滤波器的电流ili2不再是正弦波，考虑交流侧特征谐波分量的小信号模型1 的交流滤波器电流与PSCAD 详细模型的变化趋势基本一致；而仅考虑基频分量的小信号模型对应的ili2波形为典型的正弦波，与PSCAD 详细模型的差异较大。由此可见，考虑交流侧特征谐波分量的小信号模型1 相比仅考虑交流侧基频分量的小信号模型2，更能准确反映详细LCC-HVDC 模型的动态特性。

图8 LCC 逆变侧交流滤波器电流对比波形

为了进一步对比两种不同小信号模型在小信号稳定性方面的差异，以LCC 逆变站控制器为例进行对比说明。图9 为LCC 逆变站控制器参数变化时两种小信号模型对应的特征值轨迹。

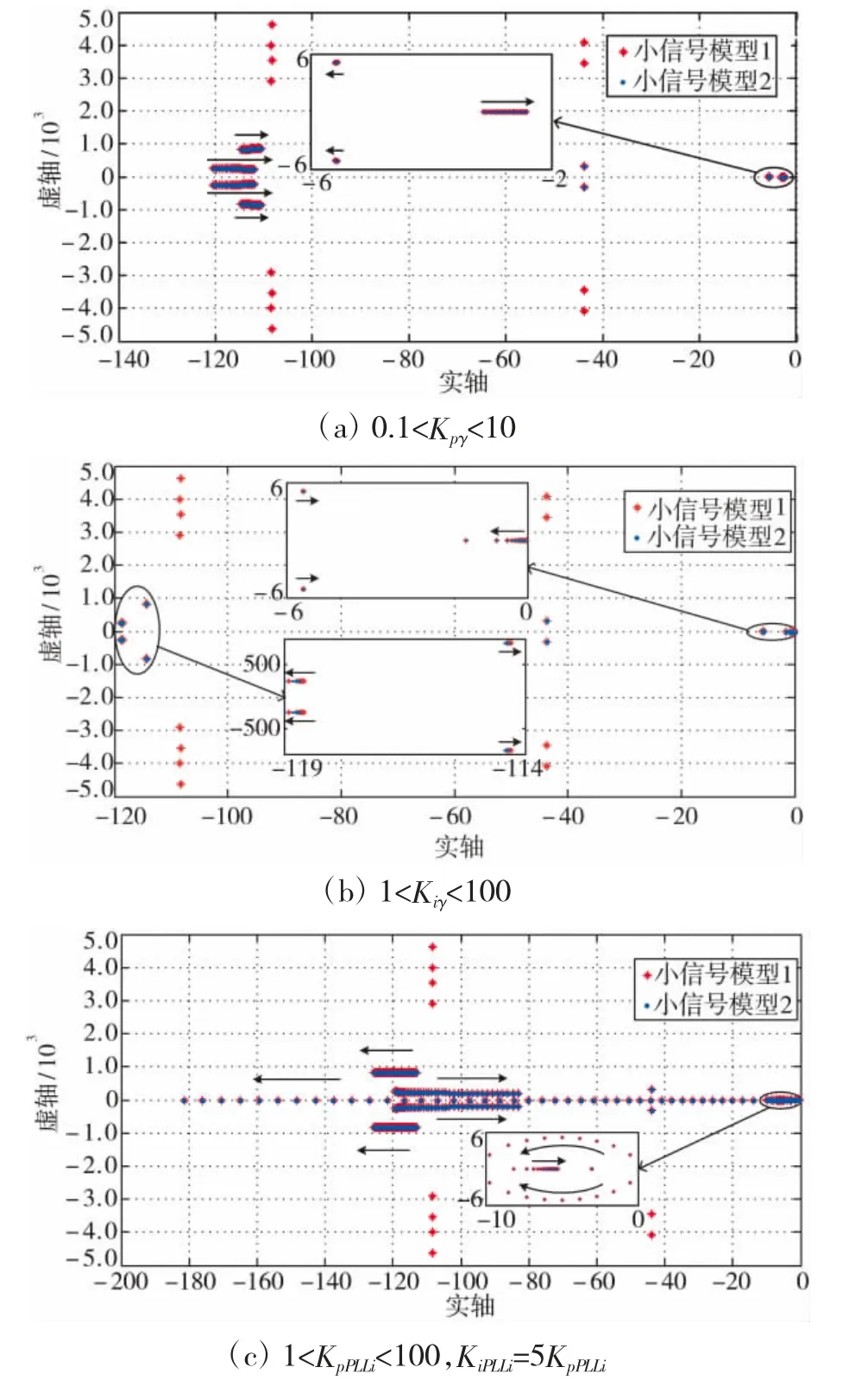
图9 LCC 逆变站控制器参数变化时两种小信号模型特征值轨迹对比

图9（a）～（b）分别为单独改变LCC 定关断角控制器的比例和积分增益系数Kpγ和Kiγ，使其分别在0.1～10 和1～100 范围内变化时对应的特征值轨迹；图9（c）为改变LCC 逆变站PLL 参数KpPLLi（KiPLLi=5KpPLLi），使其在1～100 范围内变化时所对应的系统特征值轨迹。从图中可知，当LCC 控制器参数发生变化时，小信号模型1 相比小信号模型2 多出了几组与特征谐波相关的模态，但其较虚轴较远，对系统小信号稳定性的影响较小；而离虚轴较近，对系统小信号稳定性起决定作用的主导模态的变化趋势在小信号模型1 和小信号模型2 中保持一致，因此，从简化模型的角度考虑，仅考虑交流侧基频谐波分量的小信号模型2，能够反映控制器参数变化对系统小信号稳定性的影响。

4 结论

本文推导建立了LCC-HVDC 小信号模型，并与PSCAD/EMTDC 详细电磁暂态仿真模型进行对比，验证了所建立的LCC-HVDC 小信号模型的准确性，所得研究成果可为向军用电力系统供电的LCC-HVDC 系统的控制参数选取及小信号稳定性分析提供模型研究基础。

此外，对比分析了考虑交流侧特征谐波分量及仅考虑交流侧基频分量的两种不同LCC-HVDC 小信号模型的差异。结果表明：

1）与PSCAD/EMTDC 详细电磁暂态模型对比可知，考虑交流侧特征谐波分量的小信号模型相比仅考虑交流侧基频分量的小信号模型，能够准确反映其交流侧的特征谐波影响；

2）从两种不同小信号模型的特征值轨迹分析结果可知，两种模型下对系统小信号稳定性起决定性作用的主导模态变化趋势基本一致，从简化模型的角度考虑，采用仅考虑交流侧基频分量的LCCHVDC 小信号模型，可以有效反映LCC 控制器参数对系统小信号稳定性的影响。