K型偏心支撑钢框架结构的恢复力模型

蔡文杰，杨 扬，卢坤林

(1.安徽工业大学 建筑工程学院，安徽马鞍山 243032；2.合肥工业大学土木与水利工程学院，安徽合肥 230009)

当结构受到外部影响发生变形时，会产生趋向恢复至原状态的力，即恢复力。恢复力模型是结构在外力作用下所受力与位移间的数学模型，一般由骨架曲线模型、刚度退化规律、滞回规则组成。恢复力模型可反映结构在外力作用下每个时刻的力学特征，能直观表征结构受力过程中的弹塑性变化，帮助确定结构所处状态及修正退化后刚度。

恢复力模型在钢筋混凝土结构中的应用较多，如Yamao 等对加筋短拱肋平面内外弯矩相互作用曲线的恢复力模型进行数值模拟，分析混凝土楼板刚度和相互作用曲线对其结构的影响；李宏男等、王义俊等建立了钢筋混凝土剪力墙恢复力模型。另外，学者们针对混凝土不同构件如方钢管高强混凝土双向压弯构件，弯矩、剪力和循环力矩共同作用下加固钢筋混凝土箱形梁，型钢和带肋薄壁复式钢管的混凝土柱，掺骨料混凝土框架边节点等建立了恢复力模型。近年对钢结构特别是对偏心支撑钢框架结构恢复力模型的讨论逐渐增加，连鸣等针对耗能梁段屈服剪切型的Y形高强钢组合偏心支撑钢框架建立了恢复力模型；郑山锁等通过不同锈蚀程度的钢框架梁开展循环加载试验，建立了恢复力模型。对于偏心支撑钢框架恢复力模型，Sullivan认为除耗能梁段变形外，支撑和柱轴向变形对层间位移也有影响；石永久等通过试验发现，结构在耗能段翼缘和柱脚支撑节点部位发生破坏；郭兵等发现，结构塑性变形主要在节点域、耗能段、梁柱节点处产生；杨扬等发现，结构支撑下节点板随荷载影响会发生屈服，并给出了一种改进后的支撑节点形式。上述文献表明，对于偏心支撑钢框架结构的研究多集中于耗能梁段，较少关注支撑连接节点部位的破坏。鉴于此，以不同支撑节点角度的K型偏心支撑钢框架为研究对象，基于有限元模拟的计算结果建立恢复力模型，以期为K型偏心支撑钢框架结构的弹塑性变化及抗震研究提供参考。

1 K型偏心支撑钢框架结构有限元模拟

1.1 有限元模型的建立

利用ABAQUS 软件建立K 型偏心支撑钢框架结构有限元模型，模型为按1︰3 比例缩小的单层单跨K 型偏心支撑钢框架。结构钢材为Q235，模型跨度2.2 m，层高1.2 m，耗能梁段截面尺寸H200 mm×100 mm×6 mm×8 mm，框架柱截面尺寸H150 mm×150 mm×7 mm×10 mm，支撑截面尺寸H100 mm×100 mm×6 mm×8 mm。剪切屈服型耗能梁段长度

e

符合《高层民用建筑钢结构技术规程》设计要求，

e

≤1.6

M

/

V

(

M

为耗能梁段全塑性抗弯承载力，

V

为耗能梁段全塑性抗剪承载力)，为确保结构抗震耗能效果最大化，选择耗能段参考长度

e

≈1.3

M

/

V

= 0.363 m，取整得

e

= 0.36 m。

以支撑在柱脚连接处的节点角度为研究变量，根据连接节点角度不同设计6个模型。当柱脚支撑节点上翼缘和支撑上翼缘位于同一直线，即延伸支撑上翼缘可使其完全与支撑节点上翼缘重合，定义支撑节点角度为0°，有限元模型见图1，具体尺寸见图2。在支撑节点角度0°的基础上，将其余5个结构的柱脚支撑节点上翼缘绕支撑上翼缘和支撑节点上翼缘的连接处，分别逆时针旋转10°，20°，30°，40°以及使柱脚支撑节点上翼缘逆时针旋转52°至完全垂直于柱的翼缘，定义支撑节点的角度为10°，20°，30°，40°及52°，支撑节点有限元模型见图3。

图1 K型偏心支撑钢框架结构有限元模型Fig.1 Finite element model of K-eccentrically braced steel frame structure

图2 K型偏心支撑钢框架结构尺寸及加载点位置示意图(单位：mm)Fig.2 Diagram of size and loading point of K-eccentrically braced steel frame structure(unit:mm)

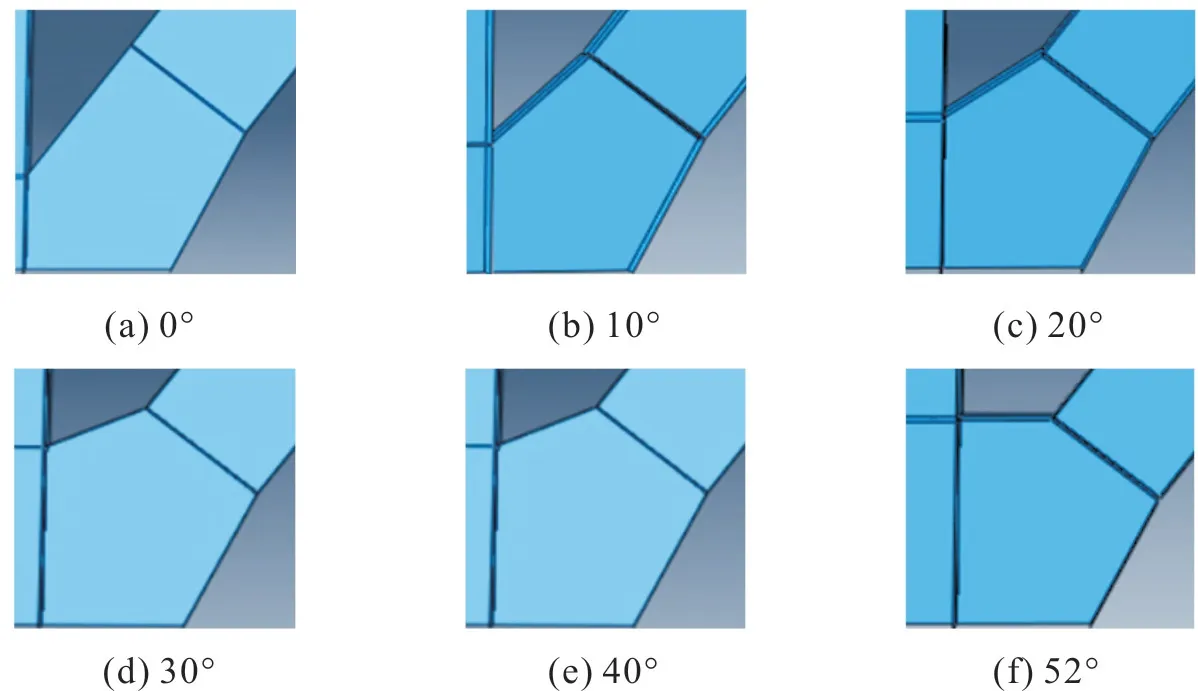
图3 不同支撑节点角度有限元模型Fig.3 Angle finite element models with different support node angles

有限元模型中选择三维八节点六个自由度的一般壳单元，通过Q235 钢拉伸试验测试Q235 钢的力学性能，结果见表1。考虑材料非线性，本构关系选择三折线模型，如图4，弹性模量

E

=2.0×10MPa，泊松比0.3。网格划分选择线性四边形结构壳单元S4R，同时对耗能段、支撑、柱脚支撑节点等重点部位的网格加密，以提高计算精度。各部件连接选择绑定约束，柱脚和支撑节点底部完全固结，使其6个方向自由度为0，结构中的连接为刚接，故不考虑接触非线性。所有的分析步均采用静力通用分析，几何非线性按钮保持在打开状态。

图4 本构模型Fig.4 Constitutive model

表1 Q235钢的力学性能Tab.1 Mechanical properties of Q235 steel

将两个柱顶板分别耦合至其中心点，在两个耦合处施加恒定竖向集中力。水平循环加载采用位移控制，加载点位于框架梁的中心延长线上。竖向和水平加载点位置如图1。规定水平循环加载作动器向左运动(推)为正，向右运动(拉)为负；以每次1 mm 位移逐渐递增，每级位移循环1 次。加载制度如图5，水平荷载下降至峰值荷载的85%时结束模拟。

图5 加载制度Fig.5 Loading system

1.2 滞回特性的模拟分析

选择有限元模拟中的水平循环荷载加载点绘制滞回曲线，不同支撑节点结构的有限元滞回曲线如图6。由图6 可看出：循环加载作用下，K 型偏心支撑钢框架具有良好的耗能抗震能力，各模型滞回曲线具有相似变化规律，整体为匀梭形，形状饱满均匀；弹性阶段，滞回曲线基本在同一直线处重合，包围面积很小；随着耗能梁段屈服，结构进入弹塑性阶段，滞回环不断增大饱满，耗散能量也逐渐增大。

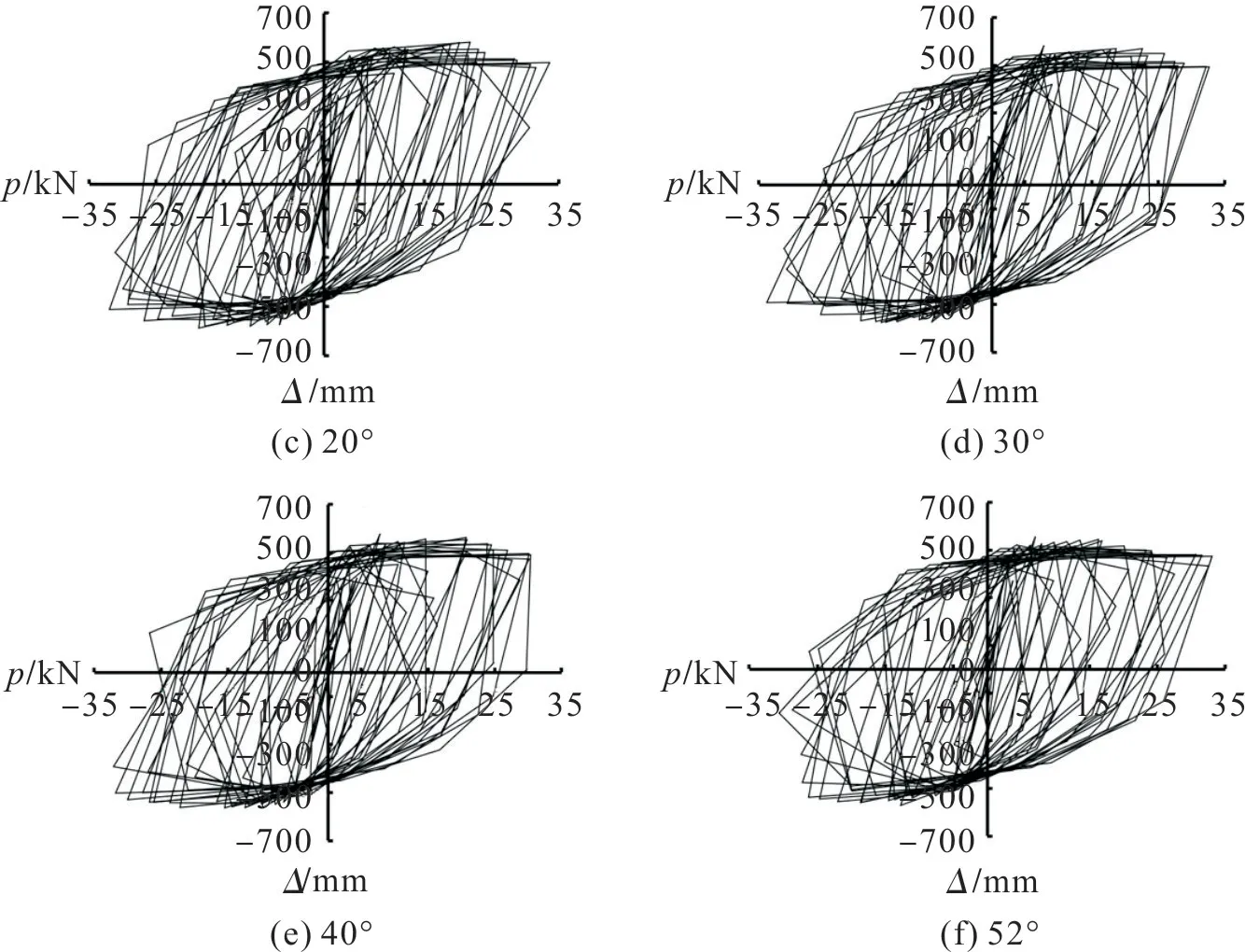
图6 不同支撑节点角度结构的有限元滞回曲线Fig.6 Finite element hysteretic curves of structures with different support node angles

2 K型偏心支撑钢框架结构恢复力模型的建立

在循环加载结构的滞回曲线中，提取逐级加载中各滞回环对应的峰值点，将其逐一连接得到荷载-位移关系曲线即骨架曲线，结果如图7。由图7可知：不同支撑节点角度的模型骨架曲线并未发生大范围波动，且具有相似变化规律和相近特征点，曲线均表现为常见的三折线形式，存在弹性上升阶段、塑性上升阶段、塑性下降阶段；峰值点后结构荷载下降并不强烈，未出现明显断崖式下降，表明K型偏心支撑钢框架结构具有较好的变形能力。选取图中位置居中支撑节点角度20°模型的骨架曲线模型为拟合对象，剩余模型骨架曲线为验证对照，参与检验计算所得恢复力模型准确性的过程。

图7 有限元模拟骨架曲线Fig.7 Skeleton curves of finite element simulation

2.1 骨架曲线模型

提取支撑节点角度20°结构的骨架曲线特征值，并将其无量纲化，结果如图8。无量纲化骨架曲线特征值分布如图9。其中：

p

表示模拟过程中结构所受最大荷载；

Δ

表示模拟过程中结构所受最大荷载对应的位移。

图8 无量纲化骨架曲线特征点Fig.8 Feature points of dimensionless skeleton curve

由图9 可知，无量纲化骨架曲线特征值分布符合三折线模型。取其正负两个加载阶段的屈服点、峰值点、破坏点共6个点作为特征点，如表2。其中：

OA

段为正向加载的弹性阶段，

A

点为正向加载屈服点；

OD

段为负向加载弹性阶段，

D

点为负向加载屈服点；

AB

段为正向加载屈服后塑性强化阶段，

B

点为正向加载峰值点；

DE

段为负向加载屈服后塑性强化阶段，

E

点为负向加载峰值点；

BC

段为正向加载屈服后塑性破坏阶段，

C

点为正向加载破坏点；

EF

段为负向加载屈服后塑性破坏阶段，

F

点为负向加载破坏点。对各加载阶段的特征值进行拟合，得到的骨架曲线模型回归方程见表3。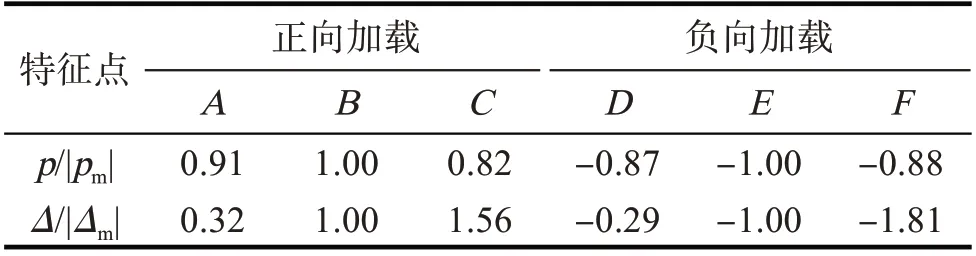

表2 骨架曲线模型特征点Tab.2 Feature points of skeleton curve model

表3 骨架曲线模型回归方程Tab.3 Regression equation of skeleton curve model

图9 无量纲化骨架曲线模型Fig.9 Dimensionless skeleton curve model

2.2 刚度退化规律

观察图6 可发现，加载过程和卸载过程均存在刚度退化情况。为方便计算，使用割线刚度代替切线刚度，研究K 型偏心支撑结构刚度变化规律。其中：

K

为正向卸载刚度；

K

为负向加载刚度；

K

为负向卸载刚度；

K

为正向加载刚度。

2.2.1 正向卸载刚度

2.2.2 负向加载刚度

2.2.3 负向卸载刚度

2.2.4 正向加载刚度

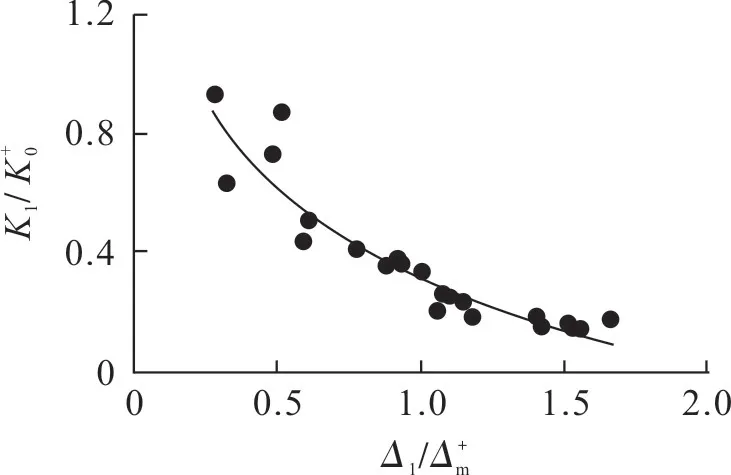
图10 正向卸载刚度Fig.10 Positive unloading stiffness

图11 负向加载刚度Fig.11 Negative loading stiffness

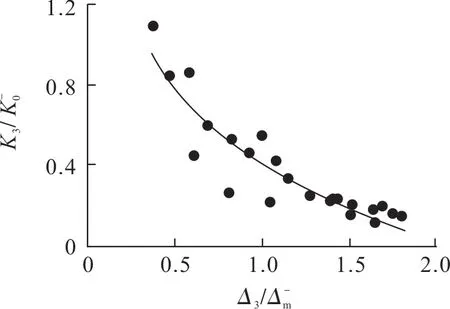
图12 负向卸载刚度Fig.12 Negative unloading stiffness

2.3 恢复力模型滞回规则

综合分析支撑节点角度20°结构的骨架曲线模型、刚度退化规律和有限元模拟的滞回曲线可知，采用三折线模型可表征K 型偏心支撑钢框架，在循环荷载作用下恢复力模型的受力特点，结果如图14。分析图14 可知，K 型偏心支撑结构恢复力模型滞回规则如下：

图13 正向加载刚度Fig.13 Positive loading stiffness

图14 恢复力模型Fig.14 Restoring force model

2)塑性阶段。结构到达屈服点

A

后，进入塑性强化阶段，荷载沿骨架曲线

AB

段变化至点

a

。在点

a

处沿

ab

段开始卸载，

ab

段为结构正向卸载路径，

K

为正向卸载刚度；卸载至零点

b

，从

b

点沿

bc

段开始负向加载，

b

c段为结构负向加载路径，

K

为负向加载刚度；结构加载至点

c

，从

c

点沿

cd

段开始负向卸载，

cd

段为结构负向卸载路径，

K

为负向卸载刚度；结构卸载至零点

d

，从

d

点沿

da

段开始正向加载，

da

段为结构正向加载路径，

K

为正向加载刚度；之后，结构荷载沿着骨架曲线到达下一级正向卸载点，继续按照正向卸载-负向加载-负向卸载-正向加载路径进行循环加载，直至停止。

3 K型偏心支撑钢框架结构恢复力模型的验证

利用恢复力模型计算支撑节点角度0°，10°，30°，40°，52°结构的骨架曲线，对比有限元模拟得到的相应支撑节点角度20°结构的骨架曲线，结果见图15。由图15可发现：采用恢复力模型计算得到的曲线符合骨架曲线的理论变化规律，存在弹性阶段、塑性强化阶段以及塑性破坏阶段；恢复力模型骨架曲线与有限元模拟骨架曲线局部出现细微差别，但整体吻合度较高，表明建立的恢复力模型满足一般工程需要的适用性和准确性要求。

图15 不同支撑节点角度结构的有限元模拟与恢复力模型骨架曲线Fig.15 Finite element simulation and restorative force model skeleton curves of structures with different support node angles

4 结 论

利用ABAQUS 软件建立6 种支撑节点角度的K 型偏心支撑钢框架结构有限元模型，对循环加载条件下6种结构模型的滞回特性进行有限元分析，建立K型偏心支撑钢框架的恢复力模型，得到如下主要结论：

1)6 种结构骨架曲线均表现出饱满圆润的滞回特性，表明K 型偏心支撑钢框架结构具有良好的耗能抗震能力；

2)6种结构骨架曲线在峰值点后结构荷载下降并不强烈，均未出现明显断崖式下降，表明K 型偏心支撑钢框架结构具有较好的变形能力；

3)恢复力模型骨架曲线与有限元模拟骨架曲线局部出现细微差别，整体吻合程度较高，表明建立的恢复力模型具有较高的准确性和可靠性，可为循环加载情况下K 型偏心支撑钢框架结构的弹塑性变化及其后续抗震性能研究提供参考。