不同对流层天顶延迟模型在中国西北地区适应性研究

王旭科 闫世伟 赵 红 杨晓磊

1 兰州资源环境职业技术学院测绘与地理信息学院, 兰州市窦家山36号，730021 2 国家自然资源部大地测量数据处理中心，西安市友谊东路334号，710054 3 陕西省煤田物探测绘有限公司，西安市尚勤路66号，710005

目前削弱对流层延迟的方法主要包括外部修正法、参数估计法、模型改正法。外部修正法具有较高的精度，但成本高、难度大，难以广泛使用[1]；参数估计法精度可以达到mm级，但是在实际使用过程中往往需要对流层延迟的先验值，解算过程繁琐[2]；模型改正法具有成本低廉、需要数据量少、计算简便的特点，是目前被广泛应用于削弱对流层延迟的方法[3]。根据计算时使用的参数类型，模型改正法可分为实测数据气象模型(Saastamoinen模型、Hopfield模型、Black模型)和非实测数据气象模型(UNB模型、EGNOS模型、GPT模型、GPT2模型等)[4]。

不同对流层延迟模型的适用性和精度在不同地区表现各异[5-9]。本文借助中国大陆构造环境监测网络(crustal movement observation network of China, CMONOC)观测数据，对不同对流层延迟模型在中国西北地区的精度进行评估，旨在利用GNSS气象学理论与方法为西北地区农林业生产提供理论参考依据。

1 数据来源及解算策略

本次实验选取CMONOC中中国西北地区数据连续性好、质量优的观测站(QHGE站、XJRQ站、XJBC站、XJBE站和XJYN站)产品数据。

基于Fortran语言对GAMIT10.7软件进行二次开发，编写并加入研究的对流层延迟模型对中国西北地区CMONOC中GPS观测数据进行处理。解算过程中引入IGS观测站(BJFS站、CHAN站、SHAO站和WUHN站)进行联合解算，其目的是削弱对流层相关性；对流层参数每2 h估计一次，每天共计13组。

2 模型简介及方案设计

2.1 模型简介

本实验涉及的实测数据气象模型主要包括Hopfield模型、Saastamoinen模型和Black模型。Hopfield模型是基于全球分布的气象站探测数据提出的适用于全球范围的对流层延迟模型，静力学延迟计算如下：

(1)

式中，ΔLd为静力学延迟量，hs为测站的高程，Pd为测站表面的气压，Ts为测站表面的绝对温度。

Saastamoinen模型和Black模型是在Hopfield模型基础上改进得到的对流层延迟模型。Saastamoinen模型在计算大气温度时，将对流层划分为2个区间，并假设该区间内大气温度为常数；Black模型是将Hopfield模型在信号传播路径弯曲产生的误差加以修正得到的对流层延迟模型[10]。

非实测数据气象模型主要包括UNB3模型、EGNOS模型和GPT2系列模型。UNB3模型是一种无需实测气象参数的对流层延迟模型，其基于多年的标准大气资料推导出各类气象参数的年平均值及年变化值，按纬度每15°给出一组气象参数值，根据得到的各气象参数，进而求得对流层延迟[11]。EGNOS模型是利用欧洲中短期数值预报中心资料建立的，在北美、欧洲地区精度较高，其他地区精度较低，不适用于小区域对流层延迟误差分析[12]。GPT2模型是利用欧洲中短期数值预报中心提供的2001～2010年全球范围内的气温、气压等气象资料进行分析而建立的，GPT2w模型在GPT2模型的基础上增加了大气加权温度Tm以及水汽衰减因子，提升了水汽压的计算结果精度，并提供了空间分辨率分别为1°×1°和5°×5°格网点处的系数(分别记作GPT2w_1和GPT2w_5)。利用GPT2及GPT2w模型获取到测站位置的气象数据后，将其代入实测气象数据模型中精度最高的Saastamoinen模型，即可得到测站位置的对流层延迟数据[13-14]。

2.2 方案设计

基于Fortran语言对GAMIT10.7软件进行二次开发，引入不同对流层延迟模型分别对观测数据进行处理，并对结果进行精度评估。具体分为以下7种方案：Hopfield模型、Saastamoinen模型、Black模型、UNB3模型、EGNOS模型、GPT2w_1+Saastamoinen模型(记作GPT2w_1+Saas模型)、GPT2w_5+Saastamoinen模型(记作GPT2w_5+Saas模型)。

3 案例分析

解算2018年4个IGS站数据，选取CODE服务中心提供的对流层产品文件(时间分辨率为2 h，每天13组)作为参考值进行对比(缺失数据不参与分析)，结果如表1所示。

表1 IGS站解算ZTD与CODE产品ZTD间的 bias值和RMS值

由表1可知，借助GAMIT10.7软件解算的IGS站天顶对流层延迟ZTD与CODE中心发布的对流层产品文件的偏差在mm级，其中最大bias值和RMS值分别为2.24 mm、5.68 mm，bias绝对值的均值为1.79 mm，RMS均值为1.93 mm；BJFS站和CHAN站解算ZTD与CODE产品ZTD间的bias值为负值，而SHAO站和WUHN站bias值为正值，可能是由于各站间地理位置、气候和大汽可降水量不同造成的。上述结果进一步证实了借助GAMIT10.7软件解算天顶对流层延迟ZTD的精度是有保证的。

为了研究不同对流层天顶延迟模型在中国西北地区的精度和适应性问题，分别按照7种方案对2018年CMONOC观测数据进行解算，获取天顶对流层延迟结果，并将中国地震局GNSS数据产品服务平台提供的对流层产品文件作为参考值(精度优于1 cm)进行对比分析，分别计算解算结果和参考值间的bias值、RMS值(缺失数据不参与计算)，结果如表2所示。

由表2可知，在实测气象数据模型中，Saastamoinen模型在中国西北地区获取的天顶对流层延迟精度最高，各个测站平均bias值和RMS值分别是-1.67 cm、3.83 cm；Hopfield模型和Black模型在中国西北地区获取的天顶对流层延迟精度相当，平均bias值和RMS值分别是-3.00 cm和4.89 cm、-2.97 cm和4.63 cm，各个测站bias值和RMS值相差在mm级。在非实测气象数据模型中，UNB3模型、EGNOS模型、GPT2w_1+Saas模型和GPT2w_5+Saas模型平均bias值和RMS值分别是-4.02 cm和6.20 cm、-6.17 cm和7.96 cm、-1.50 cm和3.18 cm、-2.58 cm和4.01 cm。GPT2w_1+Saas模型在中国西北地区获取天顶对流层延迟精度最高，GPT2w_5+Saas模型精度次之，而EGNOS模型精度最低，其原因可能是EGNOS模型是使用北美、欧洲地区气象数据建立的，导致在中国西北地区气象参数精度不足。

表2 7种方案bias值和RMS值统计

为了进一步分析季节变化对对流层延迟模型精度的影响，绘制7种对流层延迟模型bias之和的时间序列，结果如图1所示。同时对解算结果的bias值和RMS值按照春(3～5月)、夏(6～8月)、秋(9～11月)、冬(12～2月)季节划分进行统计分析，在此仅给出XJBE站统计结果，如图2所示。

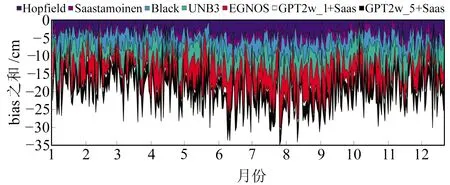
图1 不同对流层延迟模型bias之和的时间序列Fig.1 Time series of the sum of bias of different tropospheric delay models

图2 不同对流层延迟模型不同季节bias值和RMS值Fig.2 Bias and RMS values of different tropospheric delay models in different seasons

图2中柱状图形的面积表示该模型对流层延迟的偏差，即面积越小，精度越高。由图2可知，6～8月对流层延迟模型bias之和明显高于其他几个月份。在实测气象数据模型中，Saastamoinen模型bias的面积最小；在非实测气象数据模型中，GPT2w_1+Saas模型bias的面积最小。

从图2看出，无论哪种对流层延迟模型，在夏季的bias绝对值和RMS值都最大，明显高于其他3个季节，春季和秋季结果相当，冬季的bias的绝对值和RMS值最小，可能是由于夏季雨水充沛，而冬季降水量少造成的，进一步证实不同对流层延迟模型的精度受季节变化的影响；GPT2w_1+Saas模型在中国西北地区获取的天顶对流层延迟精度最高，GPT2w_5+Saas模型精度次之，而EGNOS模型精度最低，与单天对流层延迟模型精度评估结果表现一致。

4 结 语

本文借助2018年CMONOC和IGS观测数据，对7种对流层天顶延迟模型在中国西北地区的适应性问题进行分析。结果表明，解算的IGS站天顶对流层延迟ZTD与CODE中心发布的对流层产品文件的偏差在mm级，其中最大bias值和RMS值分别为2.24 mm、5.68 mm，bias绝对值的均值为1.79 mm，RMS均值为1.93 mm。在实测气象数据模型中，Saastamoinen模型获取的天顶对流层延迟精度最高，Hopfield模型和Black模型获取的天顶对流层延迟精度相当，各个测站bias值和RMS值相差在mm级。在非实测气象数据模型中，GPT2w_1+Saas模型获取的天顶对流层延迟精度最高，GPT2w_5+Saas模型精度次之，而EGNOS模型精度最低。对流层延迟模型精度受季节变化影响明显，夏季bias的绝对值和RMS值最大，春季和秋季结果相当，冬季最小，不同季节对流层延迟模型与单天对流层延迟模型精度评估结果表现一致。