EOF-LSTM神经网络的电离层TEC预报模型

2021-09-06李垠健钟正宇

大地测量与地球动力学 2021年9期

汤俊李垠健钟正宇高鑫

1 华东交通大学土木建筑学院，南昌市双港东大街808号，330013 2 华东交通大学土木工程国家实验教学示范中心，南昌市双港东大街808号，330013

电离层总电子含量(TEC)是研究电离层结构特征的重要参数，其变化趋势具有非线性、不平稳性及周期性等特点。准确预报TEC变化对卫星导航定位、航天器的控制和安全及自然灾害探测具有重要意义。

电离层TEC预报模型主要分为经验模型和数理统计模型，经验模型是根据电离层的结构和物理性质通过大量观测资料建立的，通常用于长期预报，预报精度较低[1-2]；而数理统计模型是通过数学方法对TEC时间序列进行拟合建立的，在短期预报领域精度较高[3-9]。

随着人工智能的兴起，研究人员发现，深度学习在电离层TEC预报领域具有得天独厚的优势[10-12]。长短期记忆(LSTM)神经网络通过独特的设计避免了长期依赖问题，特别适合处理和预报长时间的TEC序列，但单一的神经网络预报模型难以完全利用时间信息，易受冗余信息影响导致预报误差偏大。因此，本文利用经验正交函数(empirical orthogonal function，EOF)有效分解时间特征与空间特征的特性[13]，与LSTM神经网络相结合构建一种新的电离层TEC预报模型，简称EOF-LSTM模型。

1 模型原理

1.1 EOF分解

EOF分解是一种分析矩阵数据结构特征并提取主要信息的方法，在因子场统计组合、动力模型参数化、因子时间序列分析中已得到广泛应用，在统计预报领域往往作为统计组合的基础[14]。EOF分解可以将场的时间序列分解为不随时间变化的空间特征和随时间变化的时间系数，继而通过方差贡献率剔除冗余信息，提取集中在若干个模态分量的主要信息。主要步骤为：

1)设变量场X由m个测站的n组观测数据组成，可表示为矩阵形式：

(1)

2)将X转置并计算交叉积得到：

(2)

3)计算方阵C的特征值λ(λ1,λ2,…,λm)和特征向量V，将特征值λ按大小顺序排列，即λ1>λ2>…>λm，此时每个非0的特征值即代表对应的空间特征向量，称为EOF。将空间特征向量投影到原始资料上，得到时间系数Y：

Y=VT×X

(3)

4)利用各时间系数的方差贡献率剔除冗余信息，计算公式为：

(4)

1.2 EOF-LSTM预报模型

LSTM神经网络是一种特殊的循环神经网络(recurrent neural network，RNN)，其在RNN的基础上增加了隐藏神经元，解决了长序列训练过程中的梯度消失和梯度爆炸的问题[15]，其内部结构如图1所示。

图1 LSTM神经网络内部结构Fig.1 Internal structure of LSTM neural network

LSTM神经网络单元通过遗忘门、输入门和输出门共同决定数据信息的流动，其中遗忘门的作用是筛选冗余信息，即将xt和ht压缩为0～1之间的数字以表示“遗忘”信息的程度，0表示“遗忘”所有信息，1表示保留所有信息。具体计算公式为：

ft=σ(wf·[ht-1,xt]+bf)

(5)

式中，ht-1为前一时刻的神经元输入，xt为当前时刻的输入，wf为遗忘门的权重矩阵，bf为偏置项。

输入门利用sigmoid函数决定需要的信息并与tanh函数共同创建一个更新候选值Ct，然后将遗忘门保留下来的信息、上个单元的状态信息及更新候选值相加得到的新的候选值Ct。具体计算公式为：

it=σ(wi·[ht-1,xt]+bi)

(6)

(7)

(8)

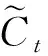
输出门则通过sigmoid函数决定单元状态中的输出部分，通过tanh函数将单元状态压缩在0～1之间，再乘以sigmoid函数运行结果得到单元的输出。具体计算公式为：

ot=σ(wo·[ht-1,xt]+bo)

(9)

ht=ot·tanh(Ct)

(10)

经过遗忘门、输入门和输出门等一系列运算反复训练后，可得出数据序列之间的函数关系，最后将隐藏层的输入值进行全连接运算得到预报值。具体计算公式为：

yt=Whyht+by

(11)

EOF-LSTM预报模型的具体步骤为：

1)将区域格网点的TEC时间序列组成矩阵并进行EOF分解，得到空间特征矩阵和时间系数向量；

2)分别计算各时间系数的方差贡献率，剔除方差贡献率小于0.001的冗余信息，并利用LSTM神经网络预测主成分时间系数向量；

3)将空间特征矩阵与预测得到的主成分向量重构，得到各格网点的TEC预测值。

2 实验结果与分析

2.1 数据选取与评定指标

本文利用欧洲定轨中心(CODE)提供的GIM产品进行分析，通过内插得到云南及其周边地区(98°～106°E，22°～28°N)20个格网点数据，空间分辨率为2°×2°。研究区位于中低纬度地区，全年光照充足，TEC的昼夜变化较大，可代表中低纬度地区的TEC变化规律。分别选取3月、6月、9月及12月前20 d时间分辨率为1 h的TEC数据进行分析，对应年积日为60～79、152～171、244～263及335～354，利用4个时段内前15 d的数据构建模型预测后5 d的TEC变化趋势，并利用均方根误差(RMSE)、平均残差(Δ)及平均相对精度(P)3个指标对结果的精度进行评定。具体计算公式为：

(12)

(13)

(14)

2.2 预报结果分析

为验证模型精度，分别利用单一LSTM神经网络模型和EOF-LSTM预报模型对20个格网点4个时段的数据进行预测。首先将20个格网点的TEC序列组成矩阵；然后利用EOF分解为空间特征和时间系数，并对时间系数剔除掉方差贡献率小于0.001的冗余信息，其余主要时间系数利用LSTM神经网络进行预报；最后用空间特征矩阵乘以时间系数的预报结果得到20个格网点的预测结果。受篇幅所限，文本仅选取部分结果进行展示。

图2和图3分别为2种模型在(98°E，22°N)、(100°E，24°N)、(102°E，26°N)及(104°E，28°N)等4个格网点年积日为259～263共5 d的预测结果和残差分布。从图2可以看出，随着纬度的增加，TEC呈减小趋势，最大值在后2 d发生扰动，5 d内的最小值均保持稳定，2种预报模型的预测值分布在实际值两侧，均可较准确地预测TEC的变化趋势，与单一的LSTM神经网络模型相比，EOF-LSTM预报模型的TEC预测结果与实际值更吻合。从图3的残差分布来看，2种模型的预报残差基本分布在5 TECu以内，单一LSTM神经网络模型的部分残差接近10 TECu，与其相比，EOF-LSTM预报模型的总体残差更小，预测效果更稳定。

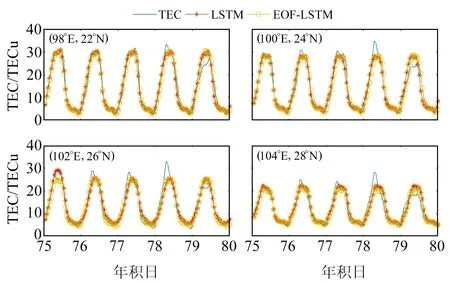
图2 不同格网点预报效果Fig.2 Schematic diagram of forecast effect of different grid points

图3 不同格网点TEC残差分布Fig.3 TEC residual distribution of different grid points

表1为4个格网点预测值与实际值的精度评价，可以看出，单一LSTM神经网络模型的RMSE均在2 TECu以上，最大为2.49 TECu，最小为2.18 TECu；而EOF-LSTM预报模型的RMSE均小于2 TECu，最大为1.88 TECu，最小为1.83 TECu，仅相差0.05 TECu，表明EOF-LSTM预报模型的预测效果更稳定。单一LSTM神经网络模型的平均残差最大为1.79 TECu，最小为1.56 TECu；EOF-LSTM预报模型的平均残差均小于1.5 TECu，最大为1.33 TECu，最小为1.21 TECu。在预报准确度方面，单一LSTM神经网络模型的最优精度为87.04%，最低精度为84.63%；EOF-LSTM预报模型的平均相对精度均在90%左右，最优精度为91.56%，最低精度为89.35%，明显优于单一LSTM神经网络模型。综上所述，EOF-LSTM预报模型的3个精度评价指标均优于单一LSTM神经网络模型，验证了该模型的预测结果具有更稳定的可靠性和更高的精度。

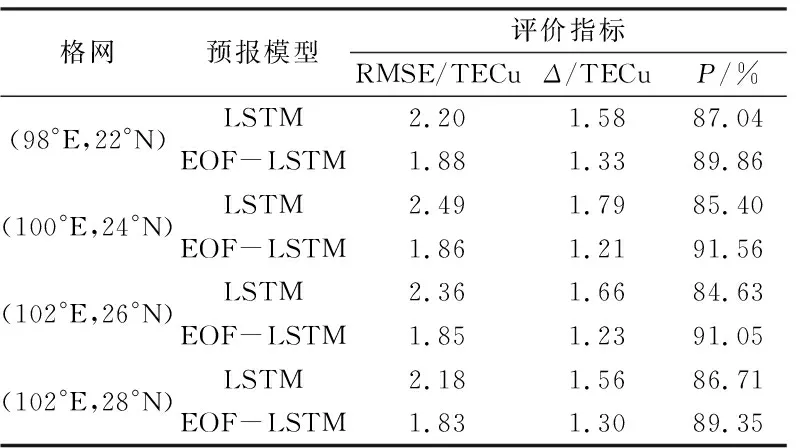
表1 不同经纬度地区2种预报模型的评价指标

地磁活动指数Kp和太阳活动指数F10.7是影响TEC变化的2个重要因素。图4为4个时段的Kp和F10.7变化情况，可以看出，在年积日为60～79时段的后5 d中，Kp指数有1 d大于2，在年积日为335～354时段的后5 d中Kp指数有1 d 大于2、1 d接近于2，其他2个时段中均仅有1 d的Kp指数大于2。表明年积日为60～79时段的地磁活动最为剧烈，年积日为335～354时段的地磁活动较剧烈，其他2个时段的地磁活动相对平静。而F10.7指数只有在年积日为152～171时段中的后2 d超过80，其余时段均在80以下，说明4个时段的太阳活动均不剧烈。

图4 不同时段的Kp指数和F10.7指数Fig.4 Kp index and F10.7 index in different time periods

为进一步验证本文预报模型的可靠性，选取4个不同时段的预测结果进行分析。图5和图6分别为4个不同时段的预测结果和残差分布。可以看出，在地磁活动剧烈的2个时段，TEC变化有明显波动，与磁静日相比在极大值处扰动剧烈，日周期性更显无序，预测结果在极值点处的误差明显偏大，反映地磁活动对电离层TEC的日变化有很大影响。从图6还可看出，地磁活动剧烈的2个时段的预报残差明显比地磁平静时期的预报残差大，单一LSTM神经网络模型的预报残差最高达15 TECu，EOF-LSTM预报模型的预报残差则基本稳定在10 TECu以内。

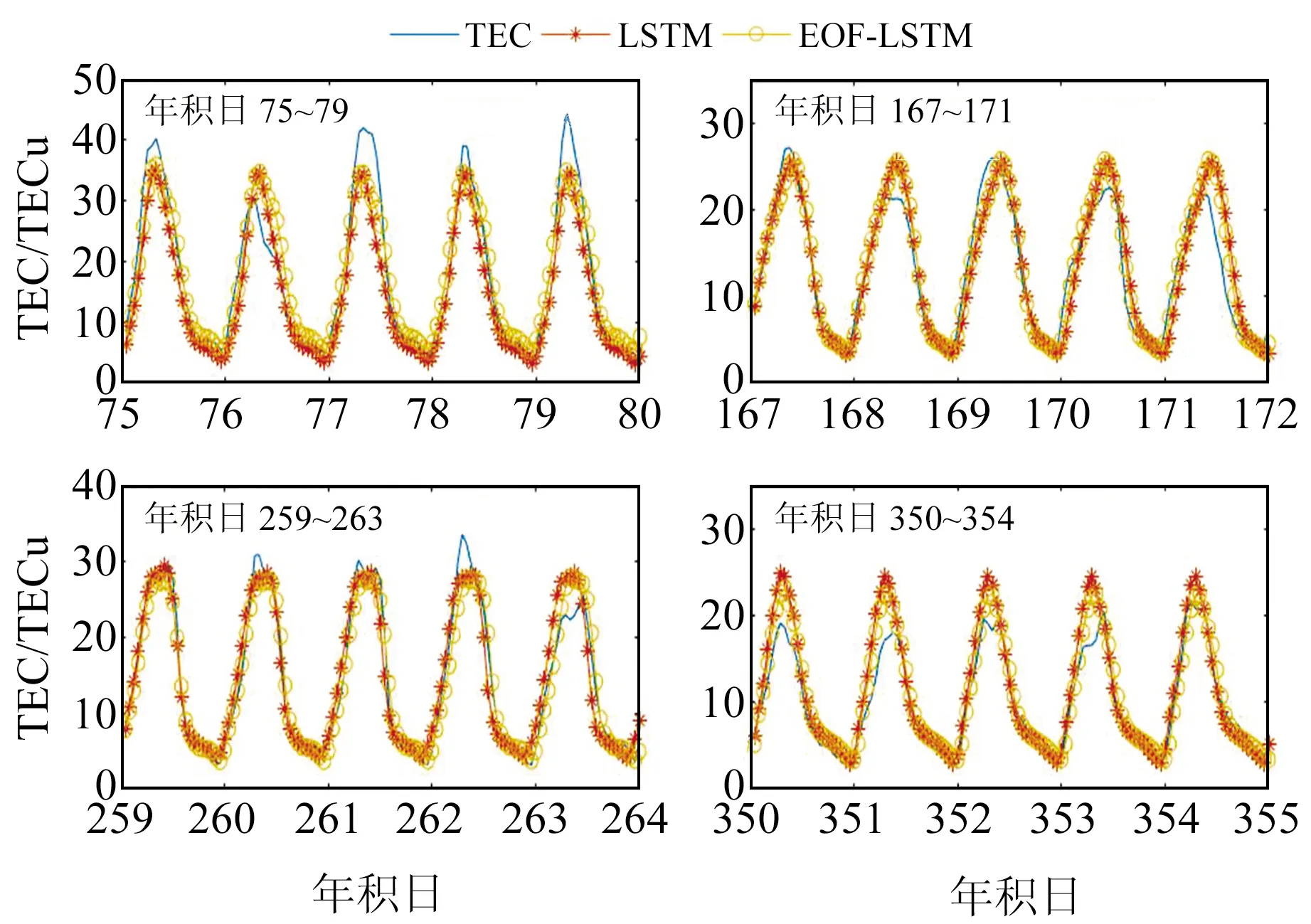
图5 (104°E，24°N)观测点预报效果Fig.5 Schematic diagram of forecast effect at observation point (104°E，24°N)

图6 (104°E，24°N)观测点不同时段TEC残差分布Fig.6 TEC residual distribution diagram in different time periods at observation point (104°E，24°N)

计算4个时段的精度评定指标和残差百分比，统计结果见表2和表3(单位%)。可以看出，在地磁活动最剧烈的时段(年积日75～79)，单一LSTM神经网络模型预测结果的RMSE为4.47 TECu，平均相对精度为82.27%，平均残差为3.31 TECu，|Δ|>4.0的预报值高达34%；而同一时段EOF-LSTM预报模型预测结果的RMSE为3.55 TECu，平均相对精度为84.53%，平均残差为2.46 TECu，|Δ|>4.0的预报值仅为20%。在地磁活动较为剧烈的时段(年积日350～354)，单一LSTM神经网络模型与EOF-LSTM预报模型预测结果的RMSE分别为2.62 TECu和1.93 TECu，平均残差分别为1.75 TECu和1.33 TECu，平均相对精度分别为83.88%和87.11%，|Δ|>4.0的预报值分别为13%和9%，进一步验证在地磁活动剧烈的条件下，EOF-LSTM预报模型具有更高的可靠性。

表2 不同时段2种预报模型的评价指标

表3 不同时段残差百分比统计

在地磁活动较平静的时段(年积日167～171和259～263)，EOF-LSTM预报模型预测结果的RMSE分别为2.22 TECu和1.86 TECu，平均残差分别为1.55 TECu和1.29 TECu，平均相对精度分别为87.62%和90.74%；而单一LSTM神经网络模型预测结果的RMSE分别为2.71 TECu和2.48 TECu，平均残差分别为1.92 TECu和1.83 TECu，平均相对精度分别为83.59%和84.24%。就残差分布而言，2个时段EOF-LSTM预报模型|Δ|<1.0的预报值分别为48%和58%，1.0≤|Δ|<2.0的预报值均为23%，高于单一LSTM神经网络模型；当平均残差较大时，2个时段EOF-LSTM预报模型2.0≤|Δ|<3.0的预报值分别为11%和8%，3.0≤|Δ|<4.0的预报值分别为10%和7%，|Δ|≥4.0的预报值分别为8%和4%，均小于单一LSTM神经网络模型，说明在地磁平静时期，EOF-LSTM预报模型预测结果的残差分布基本在±2 TECu以内，优于单一LSTM神经网络模型。