基于Marchenko理论一步法压制层间多次波
2021-09-06孙红日王维红石颖徐嘉亮
孙红日, 王维红*, 石颖,2, 徐嘉亮
1 东北石油大学地球科学学院, 大庆 163318 2 “陆相页岩油气成藏及高效开发”教育部重点实验室, 大庆 163318
0 引言
对于实际地震资料来说,多次反射的存在可能会使偏移成像结果产生强的假象,对后续地震资料的速度分析和解释造成一系列问题(黄饶等,2009;郭梦秋等,2019).多次波是指向下反射一次或多次的地震波,包括自由表面多次波和层间多次波.表面多次波是在自由表面上产生下行反射的地震波,在自由表面以下向下反射的多次波称为层间多次波.目前,多次波压制方法可分为滤波法和基于波动方程的预测相减法两大类.滤波法利用多次波的周期性和可分性来区分一次波和多次波,通常要求多次波和一次波之间有良好的可区分性.基于波动方程的预测相减法是一种利用波动方程预测多次波的数据驱动方法,将预测的多次波通过自适应匹配滤波从地震记录中减去,达到压制多次波的目的.由于层间多次波与一次有效波在传播时间和速度上的差异较小等因素,层间多次波的识别和压制难度较大,层间多次波衰减是当今国内外地球物理学专家和地震资料处理工作者所面临的难题.
层间多次波的压制方法不像自由表面多次波的压制方法(Verschuur et al.,1992;王维红等,2007;石颖等,2013)发展成熟,工业上还未形成较为系统的层间多次波压制技术.目前,对于层间多次波的压制研究主要为预测和减去层间多次波的方法,如Berkhout和Verschuur(1997)提出的层间多次波压制法,Weglein等(1997)提出的逆散射级数法(Inverse Scattering Series method,简称ISS),以及Jakubowicz(1998)提出的地表数据驱动法等.对于Berkhout和Verschuur提出的层间多次波压制方法是与自由表面相关多次波衰减(Surface Related Multiple Elimination,简称SRME)算法的扩展,将波场外推到产生层间多次波的界面,并采用SRME方法对多次波进行衰减,该算法需要了解地表和多次波产生界面之间的平滑速度模型.Berkhout和Verschuur(2005)在SRME方法的基础上,通过利用共聚焦点(Common Focus Point,简称CFP)道集使得SRME方法应用于地下散射点,实现层间多次波的预测.然而,该方法仍需要识别输入数据中发生层间多次反射的边界或层位的模型信息,需要复杂的基准面重建.对于ISS,利用自由表面、点散射以及地震波在参考介质中的传播预测多次波,Löer等(2016)基于该理论提出层间多次波可以用近似振幅进行预测.该方法虽然不需要任何的先验背景信息,但面临计算量大的问题.金德刚等(2008)推导了1.5D时空域ISS层间多次波预测算法,提高了计算效率,但不适用于三维区域.Jakubowicz(1998)利用逆时数据和一次反射地震数据预测相应的层间多次波,提出了一种显式的包括两道卷积和单道相关的层间多次波预测方法.目前的层间多次波预测方法大多基于这一思想.然而,这些方法需要精确地拾取地下层位,并且依赖于自适应减法来压制地震数据的层间多次波.吴静等(2013)将该方法扩展到多个界面产生的层间多次波衰减.但是该方法仍不能较为准确的预测出层间多次波的振幅.总体来说,反射界面选择和自适应减法是不可避免的.如果速度模型不准确,界面选择会受到影响.自适应减法通常是在最小二乘意义下执行的,最小能量准则的限制可能会对一次反射波造成损伤.
当前,国际上新发展起来一种针对层间多次波的衰减方法——基于Marchenko理论的层间多次波压制策略.该方法也是一种基于波动方程的压制技术,但不需要识别层间多次波产生界面.Broggini和Snieder(2012)将Marchenko理论引入地球物理领域.该理论的核心是一组方程耦合的Marchenko方程,这些方程可以迭代求解所谓的聚焦函数.聚焦函数可在地下介质中聚焦于任何期望点,并且充当产生或记录格林函数的虚拟点源或虚拟接收器.Broggini等(2012)和Wapenaar等(2013)将其发展到二维和三维.Meles等(2015)首次将Marchenko理论自聚焦技术用于压制层间多次波.其方法是通过虚源点与地表之间的直达波记录和地表反射响应得到上下行格林函数.然而,Marchenko理论自聚焦压制层间多次波技术仍然需要利用全局或局部匹配滤波器来从测量数据中减去预测的层间多次反射波(匡伟康等,2018),最小能量准则可能会损伤或破坏一次反射波.Meles等(2016)提出了一种基于Marchenko理论基准面重定和卷积干涉的近似一次反射获得方案,该方法仍不能避免估计下行聚焦函数的直接到达值.初始下行聚焦函数的估计需要首先建立一个平滑的速度模型,然后再应用该方法进行预测和减去.因此,现有的方法局限于自适应匹配滤波器以及层间多次波压制过程中的模型信息.该理论近些年被扩展到地表相关多次波(Singh et al.,2015,2016;Slob and Wapenaar,2017;Zhang and Slob,2019)、弹性介质(Wapenaar,2014;Da Costa Filho et al.,2014;Urruticoechea and Wapenaar,2017),以及其他许多方面.Van Der Neut和Wapenaar(2016)以及Zhang和Slob(2019)提出通过将特定深度上所有聚焦点的聚焦函数投影回采集表面上的接收器位置,消除了对初始下行聚焦函数的估计,并且不需要进行自适应减法,是一种完全数据驱动的层间多次波压制技术.本文依据该方法提出了无需先验信息和自适应相减的层间多次波压制策略,只利用地表获取的地震记录直接得到一次反射.带有高速薄透镜状地质体的数值模型测试证明了本方法的适用性.
1 理论方法
依据单边格林函数表达式和Marchenko方程,在数据域中将聚焦波场从任意深度水平投影到地表,也就是说,来自聚焦深度的一次反射作为投影聚焦波场中最后一个事件出现.该方法仍是一种迭代法压制层间多次波的方案,使得利用地表获取的地震记录直接得到一次反射.
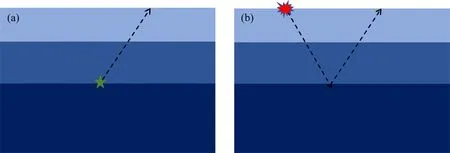
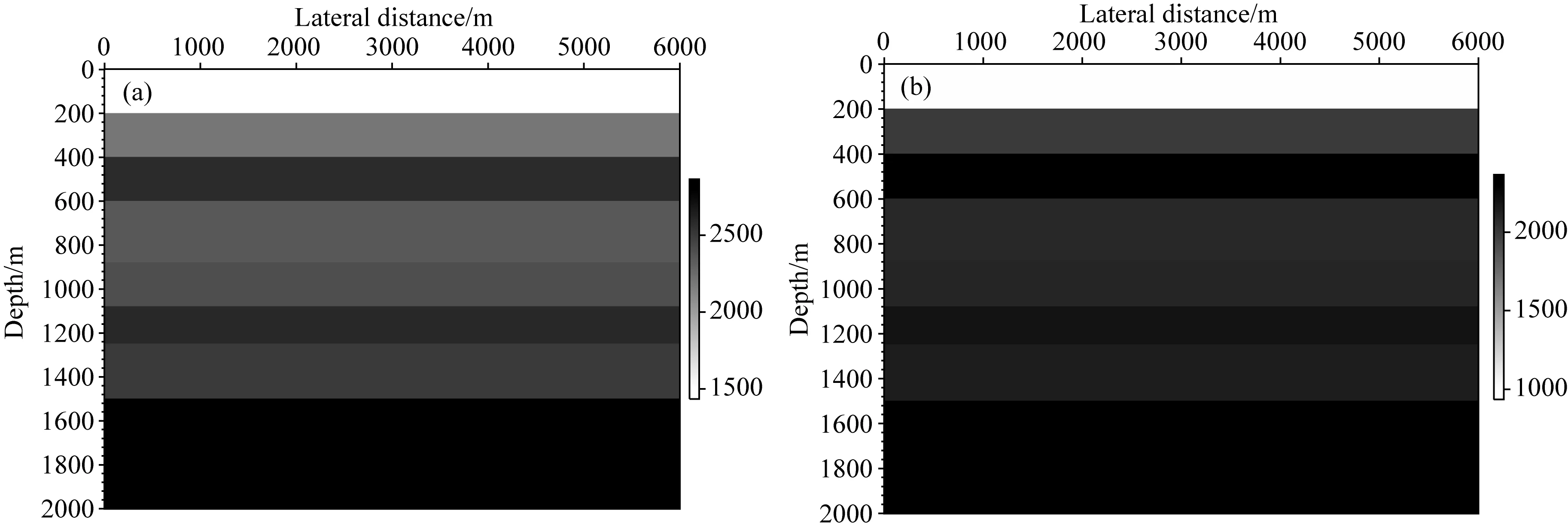
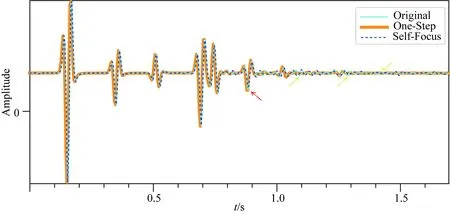
通常用t表示时间,z表示深度,(x,y)表示水平坐标.∂D0表示z0=0时的自由表面.zi表示地表以下任意深度,用∂Di表示该平面.将地表记录到的脉冲反射响应表示为R(x′0,x0,t),其中x0表示震源位置,x′0表示接收器位置,炮点、检波点均位于自由表面∂D0.格林函数G(xi,x0,t)是由在x0处激发的脉冲源定义的,并且接收器位于焦点xi处.格林函数是在与地表激发地表接收得到的单边反射响应相同的物理介质中定义的.Wapenaar等(2014)将z0 依据三维形式的通量归一化波场的单向互易定理,并将其用于深度z0和zi.当采集面z0以上的介质无反射时,格林函数可以表示为(Slob et al.,2014;Wapenaar et al.,2014): (1) (2) 其中上标“+”和“-”分别表示下行和上行波场.把下行聚焦函数和格林函数写成一个直接到达部分和一个尾波加和的形式: (3) (4) δ(x″H-xH)δ(t), (5) 式中,δ(xH)表示空间域的一个空间带限二维delta函数,δ(t)是一个时间域的时间delta函数. (6) (7) (0 (8) ×v-(x0,x″0,t-t′)dt′, (0 (9) U-(x″0,x′0,t)=R(x″0,x′0,t) (t2≤t<+∞). (10) (12) 将式(12)代入式(10),得到U-的最终表达式: x′0,t). (13) 图1 Marchenko理论一步法提取一次波示意图 (a) 聚焦点在反射界面时上行格林函数G-; (b) 聚焦点在反射界面时一次反射记录U-.Fig.1 Sketch of Marchenko one-step method to retrieve primary waves (a) Upward Green′s function G- of focus point at the reflection interface; (b) Primary reflection record U- of focus point at the reflection interface. 该方法不需要任何模型信息也不必进行自适应减法.求得的数据集一次有效波保存的更加完整,层间多次波压制效果也更好. 为验证本文方法的有效性,首先以一个简单的8层水平层状二维模型为例,进行了基于Marchenko理论一步法直接压制层间多次波方法的测试,模型如图2所示,模型大小为6000 m×2000 m,图2a为模型的速度信息,图2b为模型的密度信息. 图2 水平层状介质模型 (a) 速度模型; (b) 密度模型.Fig.2 Horizontal layered models (a) Velocity model; (b) Density model. 数值例子利用基于声波方程的高阶有限差分正演模拟,以主频25 Hz雷克子波激发,炮点位置与检波点位置重合,共501炮激发,每炮501道接收,炮间距和道间距均为5 m,采样点数1024、时间采样间隔4 ms,网格大小2.5 m×2.5 m,在模型顶部应用吸收边界条件.图3a为地表激发地表接收的包含有效波和层间多次波的单炮地震记录,并且去除了直达波. 采用Marchenko理论一步法直接压制层间多次波,得到的单炮地震记录如图3b所示.当将此结果与图3a中层间多次波压制前的地表接收地震记录进行比较时,特别是在图3箭头所指示的位置,可以很明显的看到,压制后的单炮地震记录在不损伤一次波的基础上层间多次波得到了有效衰减. 图3 第250炮地震记录 (a) 地表接收地震记录; (b) Marchenko理论一步法直接压制层间多次波结果.Fig.3 Seismic records of 250th shot (a) Seismic records of earth surface; (b) Result of internal multiples suppression directly using Marchenko one-step method. 为进一步验证本文方法的适用性,接下来对夹薄高速透镜体的二维层状模型进行测试.速度模型如图4所示,图4a为速度模型,图4b为密度模型,模型大小为6000 m×2000 m,共有8个反射边界.速度模型浅层深层均为水平层状,中间层中存在一个高速的薄透镜状地质体. 图4 带薄高速透镜状地质体模型 (a) 速度模型; (b) 密度模型.Fig.4 Models with thin high-speed lenticular geological body (a) Velocity model; (b) Density model. 图5a为利用有限差分法以主频25 Hz雷克子波正演得到的地表激发地表接收的单炮地震记录.采样记录时间4.092 s,采样间隔4 ms,网格大小2.5 m×2.5 m,道间距和炮间距均为5 m,总炮数为501,每炮接收道数501.其中,正演得到的原始地震记录中不包含自由表面多次波和直达波. 图5b显示了对带高速透镜状地质体模型的2D合成数据应用基于Marchenko理论自聚焦方法得到的层间多次波预测相减后的单炮地震记录,采用基于Marchenko理论一步法直接压制层间多次波后的单炮地震记录如图5c所示,在将两种方法的压制结果进行比较时,可以清楚地看到,基于Marchenko理论一步法压制层间多次波得到的效果更好,层间多次波被很好的消除,该方法可以在不影响一次反射波的前提下将层间多次波从地震记录中衰减干净,压制后的单炮地震记录更清晰,如图5黄色箭头处所示.观察图5b的压制结果,可以明显看出,尽管Marchenko理论自聚焦法也可压制层间多次波,但与图5c所示结果相比,压制效果相对较差,当层间多次波和一次反射相互重叠时,匹配相减滤波器无法区分它们,因此它们都会被滤波器去除.如图5所示,在应用预测相减法压制层间多次波后(图5b),红色箭头所指示的有效波的能量受到损失.分别抽取层间多次波压制前和两种方法压制层间多次波后的零偏移距单道地震记录,如图6所示,层间多次波压制前的地震记录道用浅蓝色实线表示,基于Marchenko理论一步法压制层间多次波后的地震道用橙黄色粗实线表示,基于Marchenko理论自聚焦方法压制层间多次波后的地震道用深蓝色虚线表示,从两种方法压制层间多次波前后单道地震记录对比图中可以更加直观的看出基于Marchenko理论一步法压制层间多次波的效果要优于自聚焦预测相减法压制层间多次波的效果.图7所示的局部放大图可以更清晰的显示出黄色箭头指示的层间多次波压制区.图7结果表明,在应用基于Marchenko理论的一步法压制层间多次波的结果中层间多次波被消除,而应用基于Marchenko理论自聚焦方法得到的层间多次波压制结果中存在明显的多次波能量残余.并且,图7中红色箭头所指示的有效波,在应用Marchenko理论自聚焦压制层间多次波方法后能量有所衰减,而基于Marchenko理论一步法压制层间多次波使得一次反射在时间、振幅、相位等方面都得到了很好的保留和恢复,更接近原始模型中的地震记录道.层间多次波压制前后的共偏移距剖面如图8a、b所示.图8a中的剖面包含多处多次波噪声.然而,图8b中得到的剖面几乎没有层间多次反射. 图5 第250炮地震记录 (a) 地表接收地震记录; (b) 基于Marchenko理论自聚焦预测相减压制层间多次波结果; (c) 基于Marchenko理论一步法压制层间多次波结果.Fig.5 Seismic records of 250th shot (a) Seismic records of earth surface; (b) Result of internal multiples suppression using prediction and subtraction method by self-focusing method based on Marchenko theory; (c) Result of internal multiples suppression directly using one-step method based on Marchenko theory. 图6 基于Marchenko理论一步法压制层间多次波,自聚焦预测相减法压制层间多次波与 原始零偏移距地震记录道对比图Fig.6 Comparison of zero-offset trace after suppression of internal multiples based on Marchenko theory one-step method and self-focusing of prediction subtraction method and the original zero-offset seismic record 图7 图6单道地震记录对比图中箭头指示部分放大效果图Fig.7 Enlarged view of the comparison of single-trace seismic records indicated by arrows in Fig.6 图8 共偏移距剖面 (a) 一步法层间多次波压制前; (b) 一步法层间多次波压制后.Fig.8 Common offset profiles (a) Before suppressing internal multiples by the one-step method; (b) After suppressing internal multiples by the one-step method. 基于Marchenko理论自聚焦方法压制层间多次波要求必须提供一个下行聚焦函数的初始估计(先验信息)作为迭代的初值,这在实际地震资料处理过程中带来了诸多不便.为有效解决该问题,发展了完全数据驱动的基于Marchenko理论的一步法层间多次波压制技术,通过将Marchenko方程的两侧与初始格林函数卷积,将其投影到地表,可以只利用地表获取的地震记录,在双程走时域中迭代计算一次反射波,以消除所有阶次的层间多次波. 该技术将传统的虚源点投影到地表,无需虚源点的人工选择,也就是无需初始模型参数信息,另外也无需传统方法的多次波压制的匹配滤波处理步骤,可自动实现层间多次波压制. 二维数值模型试算表明,该方法在没有任何模型信息的情况下,可有效地去除地面地震资料中的层间多次波.和传统方法对比表明,基于Marchenko理论一步法直接压制层间多次波技术的计算精度更高,可在不损伤有效波的前提下有效消除层间多次波,具有很好的保持幅性.具有很好的发展前景,可望有效应用于实际地震资料的多次波压制处理.


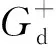
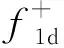

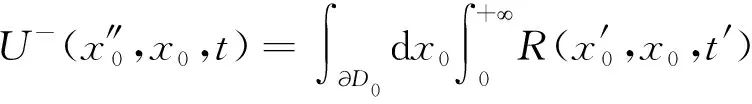



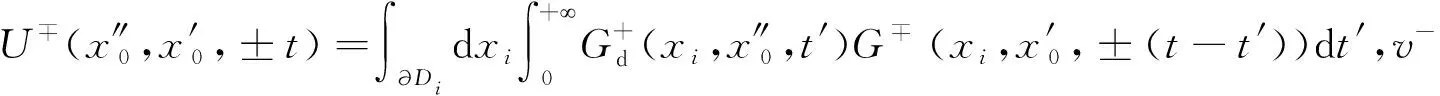


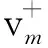
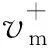

2 模型测试
2.1 水平层状模型试算

2.2 带高速透镜状地质体模型试算




3 结论
