基于三维点云的结构面产状获取方法研究

冯文凯，曾唯恐，程柯力，易小宇，焦隆新

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059)

1 研究背景

岩体结构面是岩体内发育的具有不同形态的面状地质界面，对揭露地质体结构有重要意义。传统上的调查方法需要人手持罗盘贴近岩体测量，以获取其几何要素。近年来，随着近景摄影测量、三维激光扫描等技术的发展，实现了远程非接触式地获取结构面点云数据。董秀军等[1-4]利用三维激光扫描仪调查高陡边坡，并基于PolyWorks软件解译结构面，辅助完成地质编录和后期成图。胡伟等[5]利用近景摄影测量技术试验前后结构面三维形貌数据，分析影响结构面剪切特性因素。周春霖等[6]基于双目重构技术对岩体结构面进行非接触测量并得到结构面产状。王明常等[7]以VirtuoZo数字摄影测量站为平台提取结构面特征点的三维坐标，利用Matlab程序实现岩体结构面信息的快速获取。目前对点云的操作往往要通过特殊的点云处理平台，且这些平台不具备针对地质的专门解决方案，或者存在软件版权的限制，阻碍了技术的推广。

Python语言作为一种开源的程序设计语言，具备简洁性、可读性、可拓展性等优点。本文利用Python语言，并基于最小二乘法、主成分分析法的算法原理[8-10]，构建了一套拟合平面的方法，实现了点云平面坐标向结构面产状的计算，为结构面点云的解译提供了新的轻量化方案。

2 基于Python的结构面产状获取流程

利用近景摄影测量、三维激光扫描获取到的结构面数据通常称为点云，它是一系列离散三维点的集合，共同组成了结构面的三维轮廓。为了通过点云数据获取产状信息，首先需要拟合出一个虚拟平面以得到平面方程。

2.1 最小二乘法拟合平面

2.1.1 最小二乘法拟合平面原理

最小二乘法最早出自法国数学家阿德里安，他提出让误差的平方和最小的y值就是真值(图1)。因此，拟合平面的过程可以视作寻求最小化误差下的平面函数。对于组成结构面的起伏的点云，每一个点并不总是精准地落在拟合平面中，我们用点到拟合平面的距离在Z轴方向上的投影来衡量误差，那么满足该值最小的平面即为所需要的拟合平面。

图1 最小二乘法原理Fig.1 Principle of ordinary least square

2.1.2 求解思路

设点云数据集Q=(xi，yi，zi)，(i=1，2，3，…，n)，其中x，y，z为3个维度上的位置坐标。设要求的平面方程为

z=ax+by+c。

(1)

式中a、b、c均为平面方程参数。

根据最小二乘法定律，各点到平面的距离平方和S应为最小，即

(2)

通过求其偏导并设为0以求参数，得如下方程组：

(3)

移项后用矩阵形式表达为

式(4)可转换为

AX=b。

(5)

在式子两边左乘A的逆矩阵A-1，则有

X=A-1b。

(6)

从而解出平面参数X(a，b，c)。

2.1.3 Python程序流程

本文选择Python语言设计算法，Python具备简洁性、可读性、可拓展性等优点，通过Numpy科学计算拓展库，使其具备数值计算的功能。计算步骤如下：

(1)导入点云数据集Q=(xi，yi，zi)，(i=1，2，3，…，n)。

(2)创建其系数矩阵A、常数列b，其表达式为：

(7)

(8)

(3)利用Python中np.linage.linv()求逆函数计算A的逆矩阵，即

A.inv=np.linalg.inv(A) 。

(9)

(4)用A.inv点乘b，解得平面参数X，其表达式为

X=np.dot(A.inv,b)=(a,b,c) 。

(10)

2.2 主成分分析法拟合平面

2.2.1 主成分分析法拟合平面原理

主成分分析法(Principal Component Analysis，PCA)的核心思想是将一组变量线型变换为另一组不相关的正交变量，使得变换后的第一变量方差最大，其余变量方差依次递减至可以忽略。由于方差代表了信息量，也就意味着第一变量所包含的信息量最大，前几组变量已经包含了绝大部分信息量，足以替换原始变量，最终达到降维的目的。

从几何角度来说，PCA对点云数据的降维可看作是将点云投影到另一个三维直角坐标系(图2)，3个新的坐标轴代表了3个最大主成分。如图2所示，在新的坐标系下，点云在X′O′Y′平面上方差值最大，在Z轴上方差最小，X′O′Y′平面即为最佳拟合平面，Z轴方向即为平面法向量。

图2 PCA变换原理Fig.2 Principle of princi- pal components analysis

2.2.2 求解思路

对n个包含三维坐标信息的点云数据可以用n×3的矩阵X来表示，即

(11)

为了求其主成分方向，需要找到样本协方差矩阵XTX的最大3个特征向量。由于特征向量具有两两相互正交的特征，因此前2个最大的特征向量代表了最大主成分，二者组成了拟合平面。

Python提供有“np.linalg.eig()”的函数求解特征向量，但对高维数据的暴力求解会导致计算量偏大。而线性代数中的奇异值分解(Singular Value Decomposition，SVD)法也能求解特征向量，且不需要先计算协方差矩阵XTX，因此我们引入SVD法。

2.2.3 python程序流程

(1)导入n×3阶点云矩阵Xn×3并做中心化处理。

(2)利用np.linage.svd()函数对X作奇异值分解，即

X.svd=np.linalg.svd(X) 。

(12)

得到的X.svd对象包含U，Σ，VT三个矩阵，VT称为右奇异矩阵，由样本的特征向量所组成,即

X.svd=UΣVT。

(13)

(3)取右奇异矩阵VT为

VT=X.svd[2] 。

(14)

(4)取右奇异矩阵的第3行向量(第三主成分)：

n=VT[2] 。

(15)

根据前文介绍，点云矩阵的第三主成分即为平面的法向量n，通过平面法向量可反求得平面方程。

2.3 试验点检验算法

在第2.2节中，利用Python语言分别构建了最小二乘法、主成分分析法(SVD分解)2种平面拟合算法。为了对比2种算法试验效果，生成了1 000个虚拟三维点作为试验集，试验点均满足平面方程：2x+3y+5=z，其平面参数为(2，3，5)。为了模拟出结构面本身的凹凸不平，同时加入了100个与平面稍有偏移并呈正态分布的噪声点(图3)。

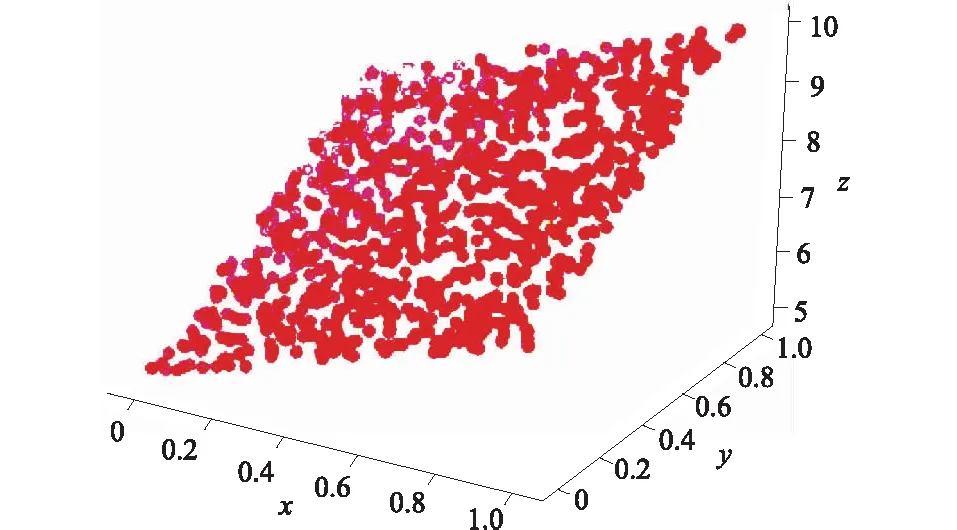
图3 建立试验点点云Fig.3 Establishment of test point cloud dataset

用上述试验点拟合平面，拟合结果如图4所示，采用最小二乘法得到的平面参数为(2.047 136，3.053 119，4.962 118)，采用主成分分析法得到的平面参数为(2.007 714，2.991 216，4.995 733)。

图4 两种算法拟合结果Fig.4 Fitting results of two algorithms

由图4可知，利用主成分分析法得到的平面方程更加精确，原因在于在最小二乘法中，需要我们不断优化的误差值d1，计算的是点与拟合平面在Z轴方向上的投影距离(图5)，而实际该值用沿平面法向量上的距离差值d2来衡量更加准确。主成分分析法则规避了这一点。

图5 误差来源Fig.5 Source of error

2.4 转化为结构面产状

为了满足地质工作要求，需要将前文所获得的平面方程参数转化为结构面产状。

一般来说，X轴代表了正东方向，Y轴代表了正北方向，Z轴指向垂直向上，它们在空间中的对应关系见图6，图中n(nx，ny，nz)为平面的单位法向量。

图6 空间大地直角坐标系Fig.6 Geodetic coordinate system

根据结构面产状的定义和图中所示几何关系可知，倾角α是结构面与水平面间夹角，也即单位法向量n在Z轴上的分量nz与Z轴的夹角。计算公式为

α=arccos(nz) 。

(16)

倾向β是其单位法向量n在水平方向上的投影与正北方向之间的夹角，根据n投影在XOY平面上象限的不同有4种情况，其计算公式可化简为如下2种：

当nx≥0时，

(17)

当nx≤0时，

(18)

由上述计算过程可知，倾向倾角的求解均需要单位法向量n，n按式(19)求得，其中a，b，c为平面方程(式1)的平面参数。

n(nx,ny,nz)=

(19)

通过上述理论在Python中编程实现了从平面方程向产状的转换，从而完成了结构面点云拟合平面并计算产状的完整过程。

3 实例验证

通过国际公开实验数据验证这套算法的适用性，结构面点云数据采集于美国科罗拉多州乌雷地区一处裸露基岩[11](图7)。

图7 结构面现场照片Fig.7 Photo of structural planes

3.1 截取点云代入计算

如图7所示，J1—J5分别代表了5块产状各异的结构面。运用“cloudcompare”软件平台从点云数据中分别截取对应的结构面点云，导入前文程序中进行计算，计算结果与参考文献[11]中结果的对比见表1。

表1 产状结果对比Table 1 Comparison of occurrence results

从表1可以看出：对于规则的结构面点云数据，计算结果与实际数据差距<2°，2种方法都有较好的拟合效果。同时观察到，二者之间的差别基本上<1°，但对于倾向较小的缓倾层面，该差值能缩小至0.1°，并随着倾向的变大而逐渐增加。其原因如第2.3节所述，是衡量误差的距离值取法不同所致，该问题在平缓结构面上表现得不明显，但差异尚不足以影响工程实际应用。

3.2 结合聚类算法自动计算

上述算法的实施需要事先设置好结构面点云数据，工程人员可以根据自己主观判断计算任意一块结构面，也可以只提取结构面中较为平整的一小块，使得结果更加精准。若是采用无监督聚类算法提前对结构面自动聚类既可以排除该过程的人工干预，同时也能提高整体解译效率。

本文选取谱聚类算法对点云进行无监督分类。该算法同样基于Python实现，这是一种基于图论的聚类方法[12]，能识别任意形状的样本空间且能获得全局最优解，相比于K-Means等常用的聚类算法，能有效应用于三维点云此类非凸分布样本。计算过程需要首先去除点云数据中无关部分，再利用谱聚类算法分簇，结果如图8(坐标轴为3个正交方向)所示，除了J1所在平面不连续而分成了4块后，其余结构面都被较好地识别，呈现较好的分割效果。

图8 谱聚类分簇结果Fig.8 Clustering results by spectral clustering

对各组结构面进行循环计算后，得到了2种算法的计算结果，数据对比见表2。

观察表2可以看出，无监督聚类后计算的结构面产状数据较真实数据出现一定偏差，但误差基本<5°，其中J5结构面本身起伏较大，难以估计，故偏差较大。在此方法中，聚类好坏直接影响到结果的准确性，同时也能看出，在有干扰点被错误聚类到结构面数据中时，主成分分析法较最小二乘法更加稳定。

表2 聚类分簇后产状结果对比Table 2 Comparison of occurrence results with clustering results

4 结 论

本文利用Python语言分别构建了传统最小二乘法和主成分分析法(SVD分解)2种算法以计算点云结构面产状。在实例中进行运用并得到以下结论：

(1)2种方法对于出露条件较好、起伏较小的结构面点云数据均有较好的拟合效果，在点云辅助地质调查中具有广泛应用前景。受误差来源影响，主成分分析法要整体优于最小二乘法。

(2)由于上述拟合方法的假设前提是待检测的结构面点云本身就是标准的平面，因此当点云数据越趋近于完整平面时，计算结果越好。对于出露条件不好或是扫描数据失真的点云数据，通过该方法计算得到的结果则偏差较大，应及时人工辅助判断。

(3)应用无监督聚类算法自动给结构面分组能有效提高产状解译速度，减少人为干预工作量，但会增大计算结果的误差。提高聚类算法的准确度能极大优化数据结果，这同时也是未来针对点云结构面的重要研究方向。