基于多元状态估计的引风机故障预警
2021-09-06曲亚鑫杨晶晶
曲亚鑫,杨晶晶
(北方工业大学电气与控制工程学院,北京,100144)
0 引言
电站设备引风机具有的特点是,具有很强的耦合性、是非线性的,并且有很多的测点。对于非线性机械设备来说,他们本身结构就很复杂、故障的类型也各式各样,会出现故障和现象无法找到映射的情况,因此很难去建立一个全面的故障知识库。且采集到的数据很容易因为外界某些因素而受到影响,导致真实的信号被掩盖。
为了解决以上问题,提出了一种基于多元状态估计法的引风机故障预警模型。多元状态估计法的建模不需要大量的故障数据,其次也不需要对单一变量分别建模,而是可以多变量一起建模。MSET方法可以快速建立描述设备正常状态的模型。观测状态和估计状态之间的差异意味着故障信息。MSET建模的核心在于过程记忆矩阵的构建,而记忆矩阵构建的核心在于数据选取。用于构建过程记忆矩阵的数据首先对其进行小波去噪,尽可能的消除噪声的干扰,之后使用主成分分析法进行降维,消除数据之间可能的相关性,以确保获得的模型具有更高的精度。
1 数据预处理和分析
■1.1 小波去噪
引风机各个观测点的实际运行状态都可以通过引风机的历史运行数据反映出来。这个数据非常的宝贵,对于数据挖掘,挖掘该设备的历史工况、健康评估等都是非常有参考价值的。但是,由于引风机实际工作中所处的环境相对恶劣,数据采集上难免受到一些干扰。例如因为传感器故障,导致采集到的数据出现的误差,环境变化导致的数据误差等等[1],这样会让采集的数据出现噪声,造成数据质量的下降,最终还会影响到模型的准确性,小波变换对给定的信号可以同时在时域和频域进行分析,并能够比较准确地辨识出信号中的突变部分以及噪声,滤噪效果非常好。
本文由于处理的数据为数字信号,因此选用db N和sym N小波,先设定分解层数为4进行小波分解,以采集的1000个引风机电机电流为例各选用9种常用的小波基对信号进行降噪处理,从重构误差和运行时间上综合比较后选择Sym5小波基。
小波分解层数的方法[2]可以确定为能量对比实验法。能量对比实验法主要参考能量分布。当正常信号和噪声信号能量分布开始分离时,整数分解层数为最佳分解层数。选择分解层数为4层。
经典阈值函数是Donoho提出的,分为软和硬两种阈值函数。硬阈值函数因为在小波域内并非连续函数,在重构过程中可能会丢失重要信号并产生振荡,因此本文后续处理采用软阈值函数进行。
进行阈值选择时,其他参数保持一致,对随机选取的连续12000个数据采用软阈值函数去噪,分别选取rigrsure规则、heursure规则、minimaxi规则、sqtwolog规则处理数据进行对比,四种不同阈值规则的评价方法对比如表1所示。

表1 不同阈值规则的评价指标对比
根据两个评价指标的数值来看,Rigrsure阈值规则的去噪效果最好。
■1.2 主成分分析法进行数据降维
主成分分析(PCA)是最常用的线性降维方法[3]。PCA的基本思想是寻找高维数据的一些主分量表示,这些分量具有最大方差,用它们表示原数据具有最小的均方误差,是一种有效的多元统计分析工具。
设引风机共有m个样本点和n个参数变量,则构成的样本集合矩阵*m nX如下:
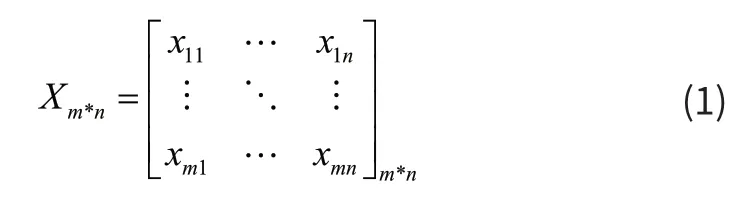
其中每一行代表某一时刻各测点的值,每一列代表某个测点在不同时刻的值。
第一步,对样本集合矩阵*m nX进行Z-score标准化处理。

得到的相关系数矩阵R:
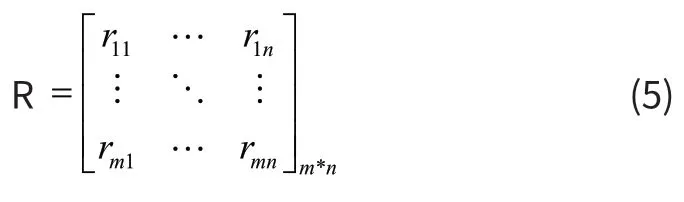
第三步,求相关系数矩阵R的特征值λ和特征向量ν。
第四步,计算引风机各监测参数变量的贡献率jc,并对λj的大小进行排序,使得λ1≥λ2≥… ≥λn。

式中λj为相关系数矩阵R的特征值。
第五步,计算引风机各监测参数变量的累积贡献率kC,以此来确定引风机主要的监测参数。
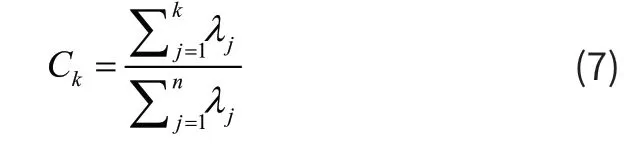
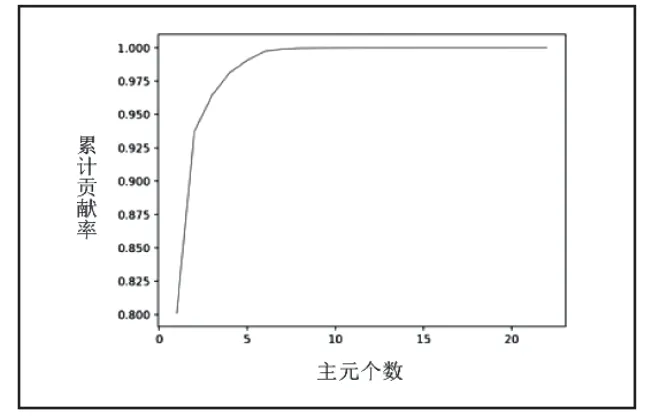
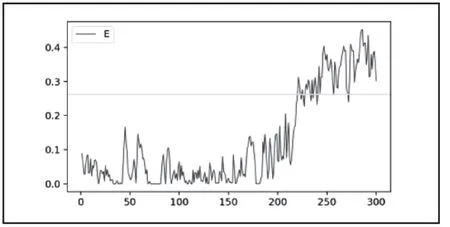
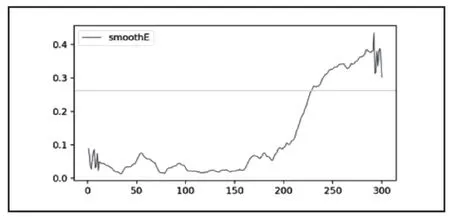
式中:k(k 工程上当Ck≥ 85%时,便可认为前k个主元保留了原始数据的大部分信息,为引风机主要的状态监测参数,从而实现了数据降维的目的。 MSET是一种非参数建模方法[4-5]。目前,MSET在核电站传感器检验[6]、工业设备状态监测[7]、电子产品寿命预测[8]和计算机软件老化现象诊断[9]等领域取得成功的应用。 利用正常运行状态下的监测数据构造历史记忆矩阵D是建立MSET模型的第一步。假设SIS系统监测到n个变量,某个采样时刻的观测向量mt可以表示为: 其中xn(tm)是采样时刻tm时变量xn的观测值。然后历史记忆矩阵D可以如下构造: 对于某时刻的新观测向量Xobs,其估计向量Xest可通过将Xobs与存储在D中的历史观测向量进行比较来计算。Xest可表示为D与权值向量ω的乘积。 权值向量ω表示estX和D中向量之间的相似性测度,可以通过观测向量obsX和估计向量estX的残差ε求得: 公式(12)中用非线性算子“ “⊗ 替代了乘法算子”ד, ⊗通常采用欧氏距离。 公式(13)应用空间距离来度量两个向量之间的相似性,通过将式(13)代入(12)和(10),可以得到估计向量Xest。可得以下公式,用来得到估计向量。 式中:1k可由工作人员根据运行经验确定,vE为残差均值绝对值的最大值。 本文所使用的数据是某电站引风机B的包括引风机前轴承温度、引风机电动机绕组温度、引风机电机电流、引风机端侧轴承水平振动等等在内的22维参数共计80000组的数据。这些数据均取自SIS数据库,为采样间隔为1分钟的连续数据,从2015/2/1日中午12点开始到2015/3/30日晚上11点59分截止。测点如表2所示。 表2 引风机B相关测点 选取x1−x22的80000组历史观测向量作为数据集data,采样间隔为1min,将历史数据分为Data1、Data2、Data3三部分。Data1是数据中的11250-71250组观测向量,从中抽样后用于构造模型的D。Data2是数据中71251到第80000组之间的观测向量,用于验证模型的准确性,进而确定故障预警阈值。前面11250组向量当做Data3,不用来构造记忆矩阵、建模,后面会从中取一部分数据检验故障检测预警的效果。 使用前面介绍的PCA方法生成一些新的线性独立分量Fi来构造记忆矩阵的行,求解R的特征值ik,相应的贡献率ic及其累积值is。对引风机的22个测点进行PCA降维分析。当选取的主元个数为3时,累积方差贡献率达到94% > 85% ,表示当使用PCA降成3维时候表明前3个主元既代表了原始数据信息,既简化了模型,又提高了模型的计算速度。为了使模型的精度更高,选取了前4个主元作为矩阵的行,把原22个变量用着4个主元来代表,可以达到95%以上的精度。图1为主元个数与累计贡献率的关系图,可以看出达到降维的目的。 图1 主元个数与累计贡献率的关系图 Data1中的数据经 PCA 和小波去噪后进行等距离采样,可以得到一个 6 ×10000的矩阵,将此矩阵作为构建MSET建模的过程记忆矩阵D。 为了验证 MSET 模型的有效性,在引风机的轴承水平振动和轴承垂直震动上从第10000到第10150个点开始人为的增加振动偏差。图2是两向量之间的残差。图3是经过滑动窗口处理后的观测值与预测值之间的残差特性曲线。 图2 向量间的残差 图3 滑动窗口后残差特性曲线 图2和图3中,黄色直线为所取阈值0.261,由公式(17)得到,根据经验,k取1.2,引风机健康状态下的最大估计残差绝对值为0.23。可以从上图中明显看出残差总体趋势是逐渐在变大的。图中选取数据段为第9851到第10150个数据,将此300点,5小时数据作为验证,从第10001点开始人为的增加偏差,也就是选取数据段的第150个点开始增加偏差。我们可以明显看到图中从第151个点开始偏差逐渐增加,残差曲线明显在上升,在滑动窗口残差统计曲线图3-3中可以看到,在第228个点左右的时候,残差和阈值到达了临界阈值处,之后继续升高,可以理解为这时候是故障的早期征兆。会进行了持续两个多小时的预警提醒,引起工作人员注意,查看是否出现了故障,为工作人员提前采取措施争取了时间,达到预警的作用。 本文以引风机为例,应用PCA-MSET方法对引风机的数据进行了故障预警。实验表明,该方法可以提前发现隐含的故障信息,在故障发生前提前预警。本文应用的故障检测方法由在线和离线两部分组成。离线部分包括数据预处理、过程记忆矩阵的构造、MSET模型的建立以及故障预警阈值的计算。在线部分利用PCA -MSET模型估计新的,然后计算其残差,从而通过判断残差是否超过故障预警阈值来实现故障测量和预警。在数据预处理中,采用小波去噪的方式对数据进行了去噪。为了降低MSET模型的复杂度,本文还讨论了基于PCA的变量选择方法。在此基础上,定义了残差,采用滑动窗口残差统计方法对残差进行处理,确定了故障预警阈值。基于PCA -MSET的故障预警方法非常适合于引风机的故障预警。2 多元状态估计技术
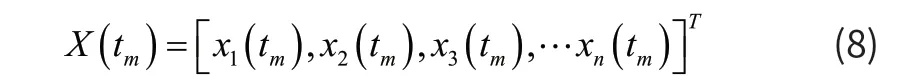
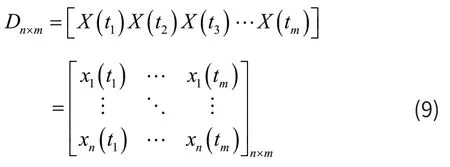


3 应用
4 结论
