车用锂离子电池SOC 估算研究
2021-09-05王海龙左付山
王海龙,左付山,张 营
(南京林业大学汽车与交通工程学院,江苏 南京 210037)
0 引言
荷电状态(state of charge,SOC)反映电池的剩余容量,是电池的剩余容量与电池容量的比值。对于纯电动汽车的电池管理系统(battey management system,BMS)来说,SOC 是重要的参数之一。对电池SOC 进行准确的估算,不仅可以提高电池系统的安全性,避免电池过充、过放,也有利于优化后续的管理与控制。同时,SOC 的实时估算也直接影响到电动汽车的整车控制与性能。然而,电池SOC 受温度、充放电率、自放电、老化等影响,很难直接通过传感器测量得到。其需要通过采集到电池的电压、电流作为基础参数,然后使用一些算法间接计算。SOC 估计必须快速、可靠、准确,以保证BMS 的高性能。但是由于电池复杂的内部化学反应,使得电池SOC 的准确估计具有一定的困难和挑战。
1 卡尔曼滤波算法SOC 估算
目前,常用的SOC 估算方法[1-2]主要有安时积分法[3]、开路电压法[4]、卡尔曼滤波(Kalman filter,KF)法、机器学习方法[5-6]以及组合算法[7-8]。在这些算法中,卡尔曼滤波法不仅可以给出SOC 的估计值,还能给出SOC 的估计误差。同时,它具有收敛快、估算精度高、对SOC 初值不敏感等优点,因而得到广泛研究。
利用卡尔曼滤波法进行电池SOC 估算[9],主要包括3 个步骤:电池模型的建立、状态空间方程的离散化及参数辨识、卡尔曼滤波算法估算。电池模型的建立是卡尔曼滤波估算SOC 的首要步骤,可以模拟复制电池各种复杂的性能并输出相应的物理参数。因此,具有高可靠性和精度的电池模型是SOC 估算的基础和关键。
2 电池模型
在电池的SOC 估算中,电池模型主要可以分为[10]:电化学模型(electrochemical model,ECM)、电等效电路模型(electrical equivalent circuit model,EECM)[11]、电化学阻抗模型(electrochemical impedance model,ECIM) 和数据驱动模型(data-driven model,DDM)[12-13]。其中,EECM 应用较多,更适合卡尔曼滤波算法SOC 估算,并且可实现电池模型精度与复杂度之间的平衡。
EECM 利用电感、电阻及电容等等效电器元件模拟电池的输出特征,不仅能较好地体现电池静态和动态特性,而且便于分析应用,通用性好。电等效电路模型包括Rint 模型、Randles 模型和nRC 模型3 种[10]。
2.1 Rint 模型
Rint 模型是一种简单的EECM,如图1 所示。
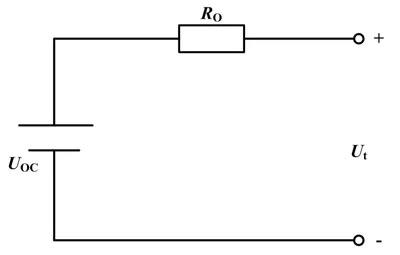
图1 Rint 模型Fig.1 Rint Model
Rint 模型通过用一个理想的电压源UOC和电池直流内阻RO串联在一起,描述动力电池的动态特性。此模型结构比较简单、易于实现,但模型精度低,且不能描述动力电池内部的极化现象,同时也忽视了锂离子电池的迟滞效应。
2.2 Randles 模型
Randles 模型最初被用于模拟铅酸蓄电池的各种特性,而后也应用于锂电池。Randles 模型如图2 所示。图2 中,CP为电池的储能电容,并行组合的Cn和Rn模拟电池的电化学极化反应;RO为内部电阻,RP为自放电电阻,模拟自放电特性。在此模型的基础上,可以加入n个平行RC 支路来分析更多的瞬态响应[14]。

图2 Randles 模型Fig.2 Randles Model
2.3 nRC 模型
nRC 模型主要由一个内部电阻(RO)和n个平行RC 分支组成。串联的RC 分支的数量可以从1 到n。对SOC 进行估算时,为了既考虑模型的精度又考虑复杂度,通常取n为1 或2。1RC 模型也被称为Thevenin模型。1RC 模型是在Rint 模型基础上,添加了一个并联RC 分支来描述电池充放电过程中的动态和瞬态响应。
Thevenin 模型如图3 所示。
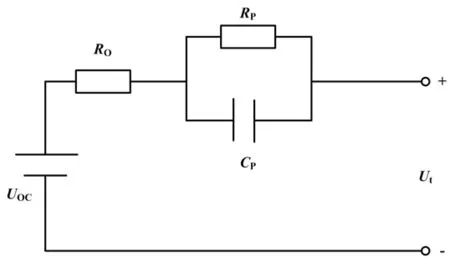
图3 Thevenin 模型Fig.3 Thevenin Model
在1RC 模型的基础上,电容Cb再与电阻RO串联,就可以构成新一代汽车合作伙伴关系(partnership for a new generation of vehicles,PNGV)模型。PNGV 模型如图4 所示。
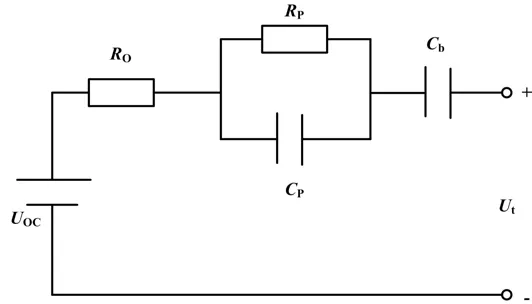
图4 PNGV 模型Fig.4 PNGV Model
该模型既可以通过电阻Rp和电容CP来描述锂离子电池的极化效应,也可以模拟SOC 变化对OCV 的影响。2RC 模型是一种用于SOC 估算的高度首选等效电路模型。与1RC 模型相比,2RC 模型精度更高。它由2 个RC 分支组成,其中:RP1和CP1用于描述锂离子电池的电化学极化反应;RP2和CP2用于描述电池的浓差极化反应。2RC模型如图5 所示。
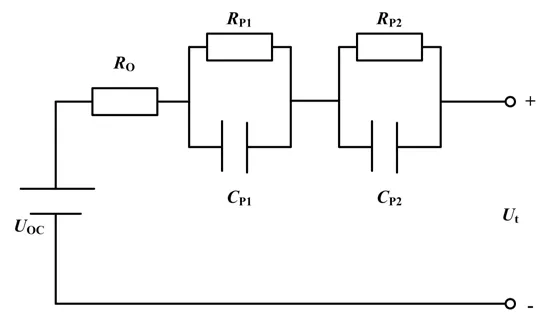
图5 2RC 模型Fig.5 2RC Model
基于卡尔曼滤波算法估算SOC 中,考虑到电池模型的复杂程度以及精度,Thevenin 模型、PNGV 模型、2RC 模型应用较为广泛。文献[14]以2RC 模型为基础,估算电池SOC。该模型对于电池的3 种特性(电化学极化反应、欧姆极化反应、浓差极化反应)都进行了考虑。相比于1RC 模型,基于2RC 模型估算电池的SOC 精度更高、误差更小。
3 状态空间方程的离散化及参数辨识
在电池模型建立后,首先根据基尔霍夫定律建立等效电路的状态空间方程。状态空间方程中包括2 个方程,分别为状态方程、观测方程。然后需要将状态方程和观测方程进行离散化处理。离散化方法主要包括解析法、有限差分、有限元、微分求积等。将状态方程和观测方程离散化的目的是为之后利用卡尔曼滤波算法估算SOC 作好准备。
步骤二是对锂电池的等效电路模型进行参数辨识。参数辨识的目的是获得电池模型的参数,包括电阻(RO、RP1、RP2),电容(CP1、CP2),开路电压(UO)等。电池模型参数可通过在线和离线2 种方式获取。离线的参数辨识方法通常是利用试验与计算的方法,获取不同SOC 状态下电池模型的各个参数值。试验的方法主要是脉冲放电方法。其计算简单、容易实现,但只能用于离线的参数估计,具有一定的局限性。同时,离线的参数辨识无法对所有电池都做这样的工作,因此辨识的电池参数应用在其他未进行辨识的同类电池时并不十分准确,适应性较差。对于已经建立的2RC 模型,文献[15]采用脉冲放电法对电池模型中的参数进行了辨识,最终得到了在不同SOC 下的各个参数大小。
在线参数辨识法主要是通过动态规划的方法,使用实时获取的、电池目前和过去的输入/输出数据,求得电池模型的参数。目前常用的参数辨识方法是基于递推最小二乘法、遗传算法等。这些方法都采用递推的在线参数辨识方法。由于计算机不需要存储和重复计算以往的全部输入/输出数据,因而对于计算机存储及计算能力要求较低。在这些算法中,递推最小二乘法用于使在线参数辨识更为广泛。文献[16]、文献[17]在2RC 模型的基础上,提出了通过递推最小二乘法对电池模型参数进行在线参数辨识。它无需存储全部数据,只需要一组观测数据,就可估计一次参数。对于参数在线实时辨识,相比较离线辨识方法,递推最小二乘法更有利于提高SOC 估算精度。
4 基本原理及非线性卡尔曼滤波算法
卡尔曼滤波算法的基本原理是利用先前估计的状态和当前测量信号递推估计当前状态。最初应用的是线性卡尔曼滤波算法。但是为了提高估算精度、解决非线性系统的问题,非线性卡尔曼滤波算法被提出。
4.1 卡尔曼滤波算法的基本原理
利用卡尔曼滤波算法估算SOC,首先需要根据电池模型建立状态方程以及观测方程,并通过变换使其离散化;然后将SOC 估算值作为内部的系统状态,利用前一时刻的SOC 估算值来预测这一时刻的SOC 估算值,并结合目前观测到的电池参数进行最优SOC 估算值的更新。不断重复上述步骤,最终得到各个时刻SOC 的最优估计值。卡尔曼滤波算法主要包括2 个部分:时间更新方程、测量更新方程。时间更新方程的主要作用是预测,即通过(k-1)时刻SOC 估算值预估k时刻的SOC 值。测量更新方程的作用是根据当前实际测量情况对上述估计值进行更新,得到最优估计值。
卡尔曼滤波算法流程如图6 所示。
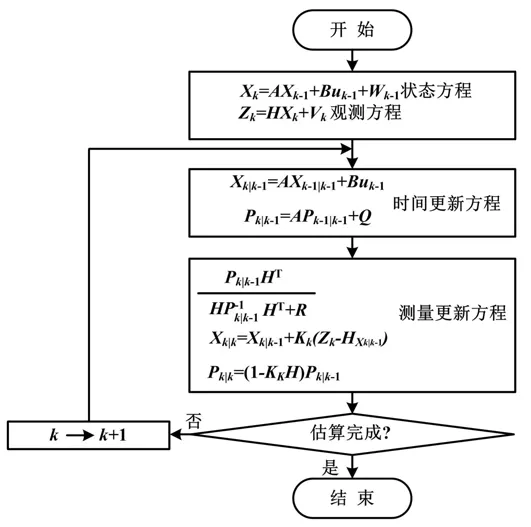
图6 卡尔曼滤波算法流程图Fig.6 Kalman filter algorithm flowchart
4.2 非线性卡尔曼滤波算法
由于电池在实际情况下是非线性的,为了提高SOC 估算精度,有必要建立非线性的状态空间方程。为了解决利用非线性的状态空间方程进行SOC 估算的问题,研究人员提出了非线性卡尔曼滤波算法。它主要分为3 大类:扩展卡尔曼(extended Kalman filter,EKF)、无迹卡尔曼(unscented Kalman filter,UKF)和立方卡尔曼(cubature Kalman filter,CKF)。
4.2.1 EKF 算法
上述利用线性卡尔曼滤波进行SOC 估算的方法,其电池模型的状态方程和观测方程是线性的。然而动力锂电池在实际工况下是非线性的。电池SOC 同放电倍率、实际容量以及温度等诸多因素成非线性的关系,会导致开路电压误差的积累。因此,需要对KF 算法进行扩展。在EKF 算法中,状态方程和观测方程是非线性的,所以需要通过泰勒公式的一阶展开:用其一阶量对非线性系统进行近似,将非线性的状态方程和观测方程线性化后,再利用卡尔曼滤波进行SOC 估算。文献[18]、文献[19]在KF 算法的基础上提出了EKF 算法,并且对比了KF 算法和EKF 算法估算电池荷电状态的试验结果。试验结果表明,EKF 算法SOC估算方法能够把误差控制在5%以内,估算精度更高。
由于在EKF 算法中,固定测量噪声协方差(R)和过程噪声协方差(Q)的假设降低了估计精度,所以引进了自适应扩展卡尔曼滤波算法(adaptive extended Kalman filter,AEKF)[20]。AEKF 在估计方法中加入了自适应更新协方差矩阵的特征,克服了误差发散和有偏解的问题。文献[21]在EKF 算法中引入了Sage-Husa 自适应算法,对噪声进行实时预测和修正。试验结果表明,相比EKF 算法估算电池SOC,应用AEKF算法估算电池SOC 的收敛速度更快、鲁棒性更好、精度更高。
4.2.2 UKF 算法
EKF 算法在线性化过程中由于忽略了高阶项,会使系统产生较大误差,导致估算精度下降;同时,状态空间方程的线性化是在先验均值附近进行的,那么在真实后验扩展中可能会出现显著的误差。为了弥补EKF 算法的不足,研究人员又提出了UKF 算法。
UKF 算法[22-23]是将标准KF 算法与无损变换(unscented transform,UT)相结合的一类非线性卡尔曼滤波算法。它通过UT 变换,使非线性系统方程适用于线性假设下的标准KF 算法。文献[24]首先分析了EKF 算法在估算中精度不高的原因,然后提出了能克服上述缺点的UKF 算法。试验结果表明,无迹卡尔曼滤波算法估算电池SOC 能将误差控制得更小(远远小于EKF 的4%),并且提高了估算精度。同EKF 一样,为了克服过程噪声和测量噪声的均值和协方差对于SOC 估计精度的影响,也需要将Sage-Husa 滤波等算法与UKF 算法相结合,得到自适应无迹卡尔曼滤波算法(adaptive unscented Kalman filter,AUKF)[25]。
4.2.3 CKF 算法
EKF 算法和UKF 算法具有发散性和维数性。为了解决这些问题,研究人员又提出了CKF 算法[26-27]。该算法的核心是球面径向容积准则。采用CKF 算法进行SOC 估计,并将结果与EKF 算法和UKF 算法进行性能比较。结果表明,与EKF 算法相比,CKF 算法具有更高的计算精度和更长的计算时间。为了提高CKF 算法的性能,再次提出了一种新的自适应容积卡尔曼滤波(adaptive cubature Kalman filter,ACKF)算法,并将其与CKF 算法、EKF 算法进行了性能比较。对比结果表明,虽然ACKF 算法的计算时间超过了CKF 算法和EKF 算法,但ACKF 算法的精度最高、收敛速度最小,对测量误差具有很强的鲁棒性。
5 结论
本文论述了卡尔曼滤波算法估算电池SOC 的主要步骤及原理,分析了不同电池模型以及卡尔曼滤波算法应用的优缺点。通过上述研究与分析,基于卡尔曼滤波算法进行SOC 估算仍然有很多需要进一步研究的问题:第一是引进先进的电池模型,能更加全面、准确地模拟电池各种特性以及不确定性,并降低其复杂度,使实用性更强;第二是卡尔曼算法应与其他算法结合使用估算SOC,不仅可以降低整体计算量,也可以起到优势互补的作用;第三就是选择更准确的适用于电池模型的在线参数辨识方法,从而减小估算误差。
