基于Copula-GARCH模型的原油市场和股票市场相关性研究

宋雪莲

(上海理工大学 管理学院， 上海 200093)

原油是基础能源和重要的工业生产原料，对促进工业发展起到巨大的作用。随着全球金融体系的快速发展，原油期权、期货、其他衍生品等金融工具的开发，原油市场更加金融化。人们将原油视为虚拟资本的投资替代品，并且不断增加对原油期货等产品的投资份额[1]。这使得原油价格的波动不仅是对宏观经济变量的外来冲击，而且增加其他金融市场的系统性金融风险。在金融领域中，股票被称为市场经济发展的“晴雨表”。在市场有效的前提下，股票扮演着市场经济预测的角色，其价格是金融研究的重要信息变量之一。因此，原油市场与股票市场之间有密切的联系。

1 文献综述

近年来随着全球对原油需求量的增加，使其在经济发展中占据越来越重要的地位。经济的增长在一定程度上推动原油价格的上涨，原油价格的增长会进一步抑制经济的发展。而股票市场不仅可以很好地反映经济发展的现状，还可以传递重要的经济信息。因此，越来越多的学者重点考察原油市场与股票市场之间的相关关系。

国外的研究最早可以追溯到1983年，Hamilton提出在第二次世界大战之后，油价的上涨是导致美国经济衰退的主要因素[2]。Ciner采用非线性格兰杰因果检验的方法证实了股票市场与油价之间的非线性关系的存在，而且两者之间的关系在20世纪90年代变得更加牢固[3]。国际原油市场与不同国家的股票市场的相关性有显著的不同。Nguyen和Bhatti采用Copula方法研究中国和越南的股票市场对油价波动的敏感程度，发现原油市场与中国股票市场之间的相关性并不显著，但是和越南股票市场之间存在着较强的相关性[4]。Conrad等研究宏观经济环境的变化对原油市场和股票市场波动性和相关性的影响。研究发现在经济长期强劲扩张期间油价和股票市场出现负相关关系，在经济衰退和复苏期间两者呈现出正相关[5]。

但是也有学者认为油价与股票市场之间不存在相互影响或者两者之间的相关关系并不显著。Jammazi和Aloui将小波分析和马尔可夫切换向量自回归模型(MS-VAR)方法相结合，研究在1989年1月至2007年12月，原油价格冲击对英国、法国和日本的股票市场收益的影响，结果表明在经济衰退时期，原油价格的波动不影响英国和法国的股票市场[6]。

中国对原油价格与股票市场相关性的研究起步较晚。诸葛尚琦等发现虽然国际原油价格与中国股市之间不存在Granger因果关系，但是通过构建VAR模型可以证明国际油价的波动与中国股票市场的波动之间存在长期的协整关系[7]。朱小能等采用移动平均法从国际原油价格中提取油价趋势因子，以此来分析油价的波动对“一带一路”沿途35个国家的股票市场的影响，结果表明国际原油价格的波动对不同国家股票市场的影响是非对称性的[8]。但是，金洪飞等以2003—2006年国际原油价格和中美两国股票市场的日数据为样本，通过构建二元GARCH模型和VAR模型，得出国际原油价格的波动不会对中国股票市场产生任何影响的结论[9]。

2 Copula-GARCH模型构建与评价

Copula-GARCH模型中不同的变量可以选择不同的条件边缘分布，这不仅优于一般的传统线性模型，而且在实际应用中更具有灵活性。所以采用GARCH模型描述两个金融时间序列的条件边缘分布，并用合适的Copula函数连接概率积分变换后的新序列，从而刻画两个序列之间的相关关系。

2.1 边缘分布模型的构建

由于金融时间序列的条件分布具有高峰、厚尾、时变、偏斜、波动群集等特征，t分布能够很好地刻画这些序列的分布特性，并且大量实证研究表明，GARCH(1,1)、GARCH(2,1)、GARCH(1,2)模型已经可以充分描述金融市场收益率序列的变化和波动。所以采用GARCH(1,1)-t模型拟合序列的条件边缘分布。GARCH(1,1)-t模型表示为

(1)

式中：μ表示收益率Rt的均值；ht表示εt的条件方差，α≥0,β≥0；t(ν)表示自由度为ν的标准t分布；收益率Rt是Xt的函数，Xt和Rt同分布；It-1为t-1时刻的信息集。

2.2 Copula函数的建立

2.2.1 常相关Copula函数的表达式

1)二元Normal-Copula函数

C(u,v;ρ)=

(2)

式中：u和v分别为股票市场和原油市场的日收益率；ρ为相关参数，ρ∈(-1,1)；φ-1为标准正态分布函数的逆函数。

2)二元t-Copula函数

(3)

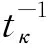
3)二元Gumbel-Copula函数

Gumbel-Copula函数的生成元φ(t)=(-lnu)δ，函数表达式为

(4)

式中，δ为相关参数，δ∈[1,+∞)。

4)二元Clayton-Copula函数

Clayton-Copula函数的生成元φ(t)=t-θ-1，函数表达式为

(5)

式中，θ为相关参数。

5)二元Frank-Copula函数

Frank-Copula函数的生成元φ(t)=

(6)

式中，λ为相关参数。

6)二元Symmetrised Joe-Clayton(SJC-Copula)函数

(7)

式中：κ=1/log2(2-τU)；γ=-1/log2(τL)；τU和τL分别为上尾相关系数和下尾相关系数。

2.2.2 时变相关的Copula函数表达式

1)二元时变 Normal-Copula函数

二元时变Normal-Copula函数与二元Normal-Copula函数形式相同，如式(2)所示，但是，式中的参数ρ是一个时变的相关参数，一般形式为

(8)

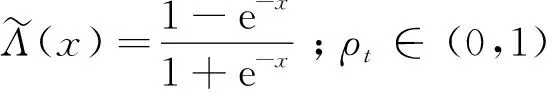
2)二元时变SJC copula函数

CSJC(u,v;τU,τL)=0.5[CJC(u,v;τU,τL)+

CJC[1-u,1-v;τU,τL)+u+v-1]

(9)

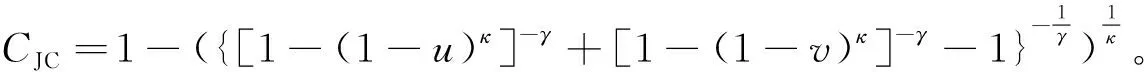
2.3 Copula模型的评价

为了检验模型的拟合效果，判断该模型是否能够描述变量间的相关关系，将极大似然值、赤池信息准则(AIC)、欧式距离等方法作为Copula模型拟合优度的评价指标。首先计算极大似然函数值和AIC值，如式(10)所示。其中LLF表示对数似然函数，k表示Copula模型中参数的个数。然后计算经验Copula函数和拟合Copula函数之间的欧式距离。最后通过比较三者数值的大小选择最优的Copula模型。AIC值越小，拟合效果越好；欧式距离越小，拟合度越高；极大似然函数值越小，对应的Copula模型越合适。

AIC=2k-2×LLF

(10)

2.4 Copula模型的相关性度量

表1 常相关Copula模型的上尾相关系数和下尾相关系数表达式

3 股票市场和原油市场相关性的实证研究

3.1 数据选取和统计性描述

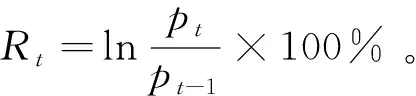
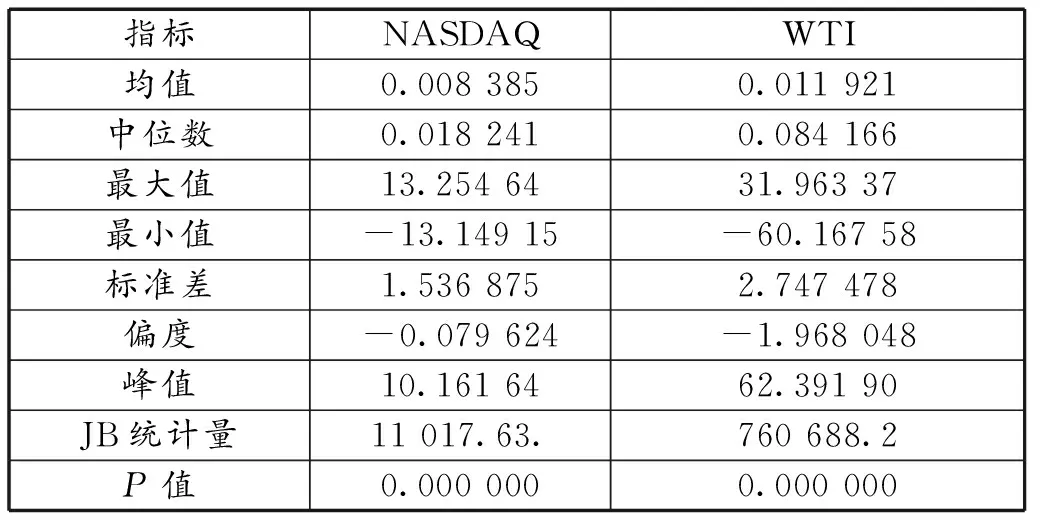
表2 NASDAQ和WTI收益率序列的描述性统计量

图1 NASDAQ和WTI收益率的时序图

3.2 GARCH边缘分布模型的构建

首先采用ADF单位根检验方法对收益率序列进行平稳性检验，结果表明两个序列均是平稳的。然后对收益率序列进行自相关检验，发现存在序列自相关。因此，在均值方程中加入ARMA项，并且在此基础上对两个序列的残差项进行ARCH-LM检验，发现F统计量和LM统计量对应的P值均小于0.05，即序列具有条件异方差特性。所以采用GARCH模型描述NASDAQ和WTI收益率序列的边缘分布是合理的。经过多次尝试， GARCH(1，1)-t模型拟合NASDAQ和WTI收益率序列的边缘分布效果最好，采用极大似然估计法对模型进行估计，结果见表3。

表3 边缘分布的参数估计和检验结果

表3中的待估参数均通过了显著性检验。根据以上数据可以得到各个拟合模型的标准化残差序列。首先对残差序列做Ljung Box检验，得到的Q统计量说明了该序列和平方序列均不存在自相关，即变换后的各个序列是独立的。接着对残差序列做ARCH-LM检验，得到的检验统计量TR^2表明该序列均不存在异方差性。然后对标准化残差序列做概率积分变化，得到新的序列，并且对新序列进行K-S检验，检验变换后的序列是否服从(0，1)上的均匀分布。表3中的K-S概率值均大于0.1，则概率积分变化后的新序列服从(0，1)上的均匀分布。所以采用以上GARCH(1，1)-t模型拟合NASDAQ和WTI收益率序列的条件边缘分布是合理的。最后分别画出残差序列的分布和对应t分布的分位数对比图(Q-Q图)，如图2所示。该分位数图直观地表明了采用上述模型拟合边缘分布的效果良好。

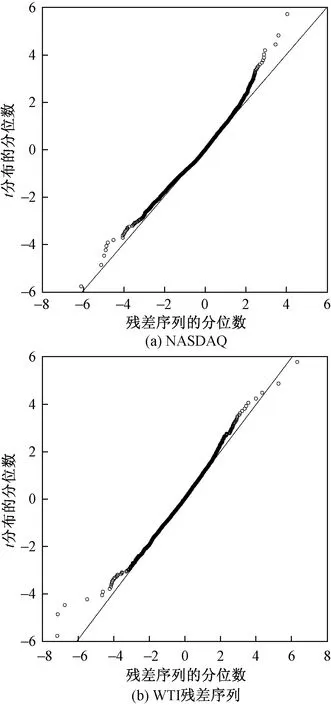
图2 条件边缘分布模型的拟合度Q-Q图

另外自由度ν和t分布与尾部形状密切相关。通过表3估计的参数可以发现，NASDAQ收益率序列的自由度比WTI收益率序列的自由度小，则NASDAQ收益率序列具有更大的尾部，其收益率出现极端值的概率比WTI收益率序列出现极端值的概率大。

3.3 常相关Copula函数的选取与模型估计

对以上边缘分布模型的标准化残差进行概率积分变换可以得到新序列，分别采用二元Normal-Copula函数、t-Copula函数、Gumbel-Copula函数、Clayton-Copula函数、Frank-Copula函数和SJC-Copula函数描述新序列之间的相关结构。采用极大似然估计法估计Copula函数的参数，结果见表4。

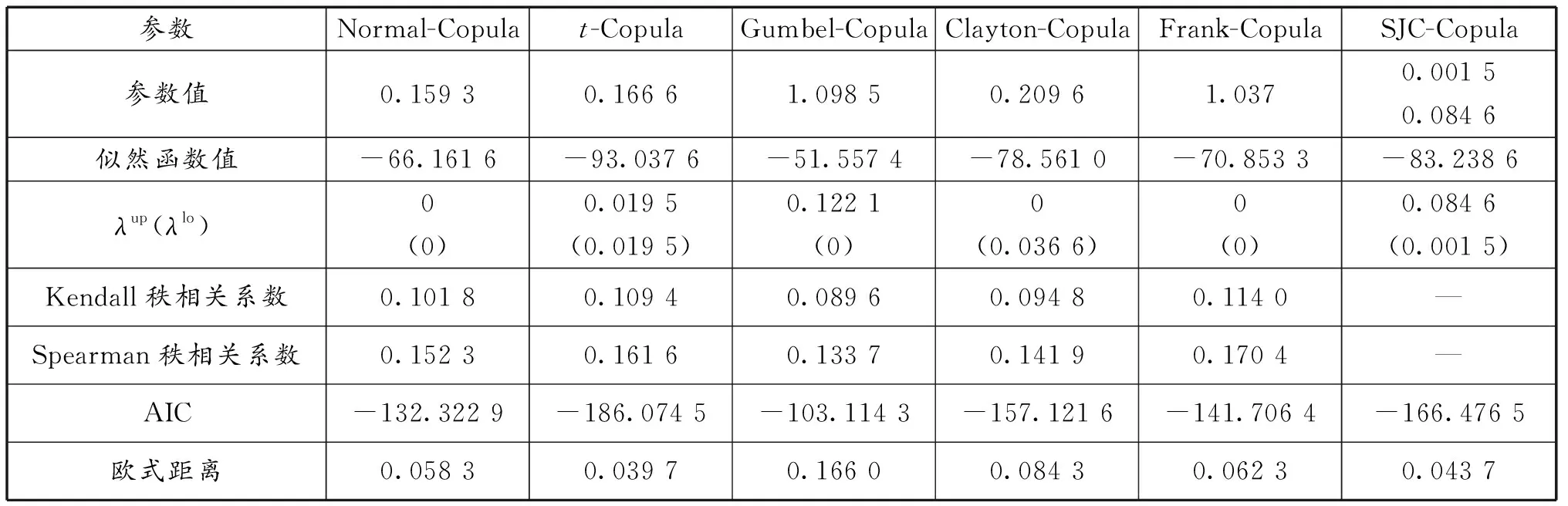
表4 常相关Copula模型的相关参数估计值

从表4中可以发现，Gumbel-Copula模型的欧式距离、极大似然值和AIC值均是最大的，即拟合效果最差，其次是Clayton-Copula模型。由于这两个模型可以较好地描述不对称的尾部相关性，所以NASDAQ和WTI收益率序列的相关关系具有一定的对称性。同时，结合上述模型评价指标可以看出，t-Copula模型的拟合效果最好，并且优于Normal-Copula模型，这说明两个收益率序列具有较厚的尾部。t-Copula模型的相关性度量指标的数值均大于零，则NASDAQ和WTI收益率序列之间具有正相关的关系，WTI原油价格上升会导致NASDAQ股价上涨，NASDAQ股价下跌会导致WTI原油价格降低。由于尾部相关性大于零，所以其中一个市场的价格飙升或者骤降会对另一个市场产生影响。图3为二元t-Copula函数的分布函数图和密度函数图。

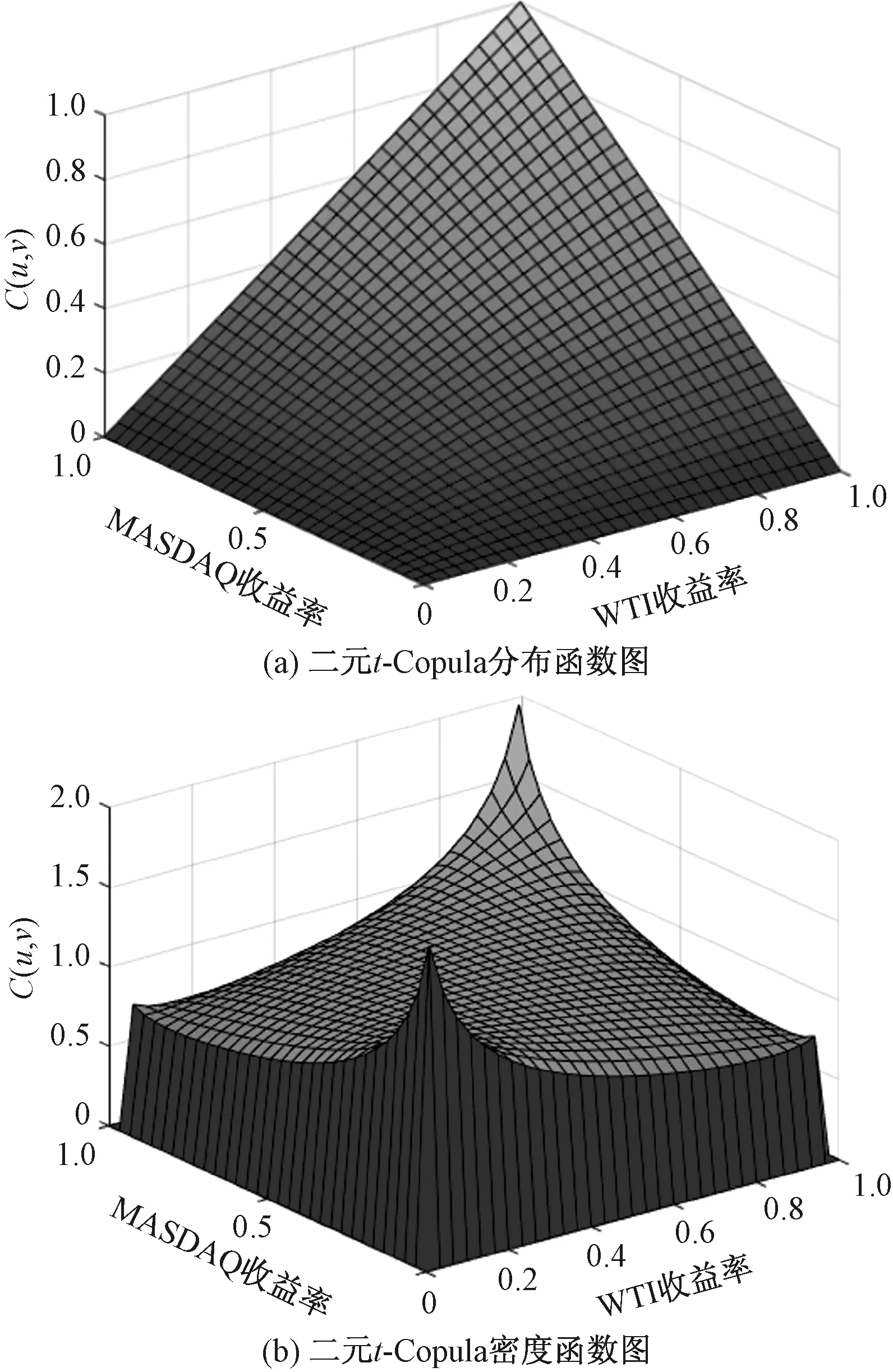
图3 二元t-Copula函数的分布函数图和密度函数图

SJC-Copula模型中的上尾相关系数略大于下尾相关系数，说明NASDAQ和WTI收益率序列的相关关系中存在略微的不对称性。以上常相关Copula模型只是描述变量间的静态相关关系，由于金融市场之间的相关关系具有一定的时变性，所以接下来采用时变相关的Copula模型研究股票市场和原油市场之间的动态相关性。

3.4 时变相关的Copula模型的参数估计

基于GARCH边缘分布模型的拟合结果，构建时变相关的Normal-Copula模型和时变相关的SJC-Copula模型。模型的相关参数见表5。

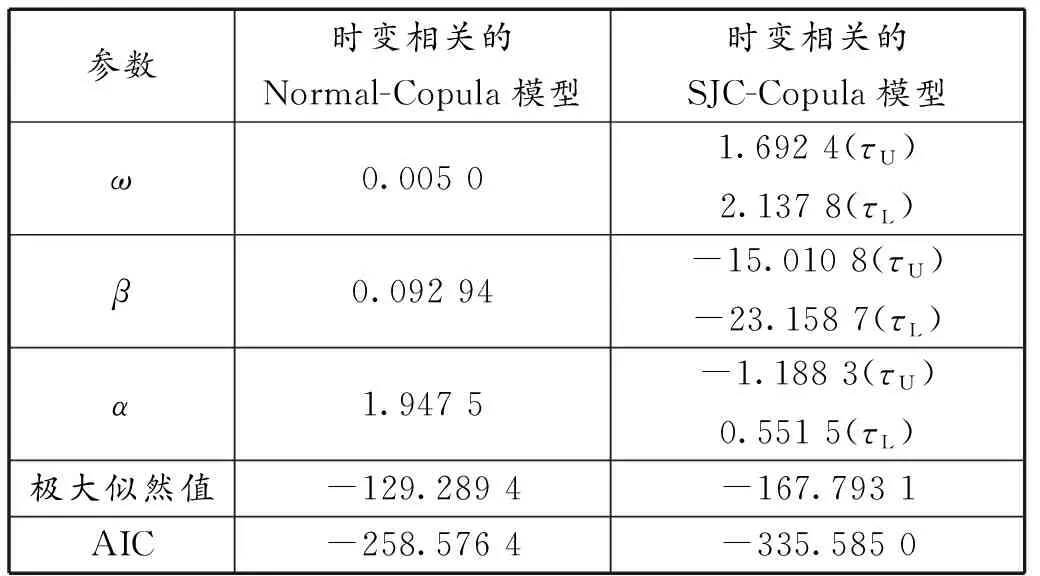
表5 时变相关的Copula模型的相关参数估计值

观察时变相关的Normal-Copula模型的参数可以发现：持续性参数β几乎接近零，这说明t-1时刻的参数值βt-1对t时刻的参数值βt没有显著的影响；外生变量参数α较大说明收益率序列之间的相关系数容易受到外生变量的影响。

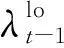
对比表5中的两个模型可以发现，NASDAQ和WTI收益率序列存在正的相关性。动态模型相关系数的一阶滞后项拟合系数β都为不为零，这意味着两个序列的相关关系具有一定的持续性。时变相关的SJC-Copula模型对应的AIC值和极大似然值较小，所以采用该模型拟合NASDAQ和WTI收益率序列的相关关系的效果较好。

比较表4和表5中的AIC值可以发现时变相关的Copula模型的拟合度优于静态的Copula模型，即采用动态Copula模型能更好地描述该序列之间的相关性。根据时变相关的Normal-Copula和SJC-Copula模型相关参数绘制时变图，如图4、图5所示。

图5 时变相关的SJC-Copula函数相关参数的时变图

由图4可知，NASDAQ和WTI收益率序列的相关关系具有一定的时变性，围绕着某一固定值上下波动，并且总体上呈现出增长趋势。其中在2008年里相关性表现为先大幅度跌至最低点，之后又上涨并达到最大值，出现这种大幅度波动说明了两个序列之间的关联机制变化性强，不确定性高。究其原因是受到全球金融危机和美国次贷危机的影响。在金融危机发生前，美国通货膨胀严重，股票市场和原油市场之间存在着过剩的流动性，导致了投机需求大量增加，从而打破了两个市场之间的联动性，降低了股票市场对原油市场的冲击，具体表现为两者的相关系数降低到-0.4左右。但随着美国次贷危机的爆发，市场流动性急剧收紧，股票市场中的恐慌情绪加速蔓延，金融传染机制的跨市场风险扩散使得两个市场之间的联动效应更加明显，相关系数增加到0.4的水平。之后随着美国经济的不断复苏，原油市场所表现出的“金融属性”逐渐降低，两个市场中的投资需求都有所减弱，经济基础层面的传统关联机制再次显现，表现为相关系数在较高的水平上小范围波动。

由图5可知，下尾相关系数大于上尾相关系数，意味着NASDAQ和WTI收益率之间的相关结构具有不对称性，并且同时出现极端值下跌的可能性更大。与时变的SJC-Copula模型的上尾相关系数曲线相比，下尾相关系数曲线较为稠密且波动幅度更大，说明两个市场的相关性在市场低迷的时候更大，下尾相关系数更容易受其他因素干扰，表现得更加敏感。

4 结论

通过构建Copula-GARCH模型研究国际原油市场和美国股票市场的相关性，基于2000年8月23日至2021年2月19日的NASDAQ股指和WTI原油价格的收益率序列进行实证分析。首先采用GARCH(1,1)-t模型估计各收益率序列的边缘分布，然后构建常相关和时变相关的Copula模型刻画两个市场之间的静态和动态相关关系，最后将AIC值、极大似然值和欧式距离作为评价指标以检验模型的拟合效果，选择最合适的Copula函数。

GARCH(1,1)-t模型可以较好地拟合具有偏斜、厚尾、尖峰等特性的NASDAQ收益率序列和WTI收益率序列的条件边缘分布。在研究静态的Copula模型时发现采用t-Copula模型描述该序列之间的相关关系时拟合效果最好。两个序列之间存在正的相关关系，并且相关结构具有一定的对称性，两者的相关关系在尾部变化时表现得更明显，即股票(原油)价格发生骤变时，会使得原油(股票)价格在短时间内发生同样的变化。之后通过时变Copula函数中相关参数的变动描述两个市场之间的动态相关关系。国际原油市场和美国股票市场之间的相关关系具有一定的时变性，时变相关的Copula模型比常相关Copula模型的拟合效果更好，且时变相关的SJC-Copula模型拟合效果最优。虽然上尾相关系数和下尾相关系数的走势大体相同，但是下尾相关系数大于上尾相关系数，说明价格同时出现极端下跌的可能性更大，即一个市场的价格下跌对另一个市场的影响大于价格上涨对另一个市场的影响。动态尾部的研究对于金融市场的风险管理具有指导意义，有助于市场监管部门认清市场走向，当出现下尾相关系数大于上尾相关系数时，提前规避风险，降低油价波动对股市的冲击。

重点研究美国股票市场和国际原油市场之间的相关性的原因是美国股票市场和国际原油市场之间的关联特征具有代表性和典型性。由于中国长期实行平滑模式的自主石油定价机制，在一定程度上阻碍了国内原油市场与国际原油市场的信息传导，使得油价调整不同步，从而导致国际原油市场与中国股票市场脱节，相关性很低。但随着中国经济的高速发展，工业化进程的加快，对原油的需求量日益增加，成品油定价和交易机制的改革以及股票市场结构的优化，股指期货制度体系的健全，风险监管机制的加强，国际化的进程加快，中国股市更加成熟和完善，研究他国股市和国际原油市场之间的互动规律和关联机制可以给中国未来的两个市场之间的风险规划和协调发展提供很好的参考和借鉴。