基于模糊理论与层次贝叶斯方法的涡轮盘疲劳可靠性分析

甘启义，黄洪钟，张晓颖，李彦锋，钱华明

基于模糊理论与层次贝叶斯方法的涡轮盘疲劳可靠性分析

甘启义1，黄洪钟*,2，张晓颖2，李彦锋2，钱华明2

（1.成都高新技术创业服务中心，四川 成都 610041；2.电子科技大学 机械与电气工程学院，四川 成都 611731）

航空发动机涡轮盘的可靠性数据来源通常是多源的，并且各数据信息来源的可信性也不同，给涡轮盘可靠性分析带来严峻挑战。为了解决这一问题，本文首先采用层次贝叶斯方法对涡轮盘的观测数据和其他多源先验信息进行融合；其次对不同来源的涡轮盘可靠性数据进行贝叶斯推理，获得各自的后验分布；最后利用模糊理论对多源信息的后验分布展开分析，形成联合模糊理论与层次贝叶斯方法的涡轮盘疲劳可靠性分析方法。将提出的方法应用到某航空发动机涡轮盘的疲劳可靠性分析实例中，验证其有效性。

航空发动机；涡轮盘；模糊理论；层次贝叶斯方法；疲劳可靠性

涡轮盘在航空发动机中主要是安装并固定叶片，起到连接作用，同时其也是航空发动机内关键的功率传递部件。涡轮盘通常承受着复杂的循环载荷作用，包括：涡轮盘高速旋转所产生的离心力、叶片旋转所产生的离心力、航空发动机运转所产生的高温高压载荷等。正是这些复杂循环载荷的共同作用，造成航空发动机涡轮盘极易发生疲劳失效。根据涡轮盘应力应变大小和种类的不同，涡轮盘的疲劳失效包括高周疲劳失效、低周疲劳失效、高低周复合疲劳失效等。其中，低周疲劳失效是涡轮盘最易发生的失效模式。因此，为了确保航空发动机能够安全可靠地运行，研究涡轮盘的疲劳可靠性有着重要意义。

目前，国内外学者对航空发动机涡轮盘展开了许多研究。Tanaka[1]和Taylor[2]基于涡轮盘的试验结果，发现采用最大应力来描述涡轮盘缺口处的疲劳过程并不适用，并进一步提出了采用临界距离的理论来预测涡轮盘疲劳寿命。Claudio[3]采用有限元仿真分析软件，基于断裂力学理论对涡轮盘疲劳寿命展开了分析及预测。Ayyappan等[4]联合涡轮盘有限元仿真数据和现场试验数据，提出基于S-N曲线的涡轮盘结构概率疲劳寿命预测方法。Witek[5]利用有限元仿真分析技术得到了涡轮盘关键部位的应力，并基于断裂力学理论和Paris-Erdogan模型，分析研究了涡轮盘关键部位的疲劳过程。Menon等[6]针对涡轮盘的低周疲劳失效，将涡轮盘关键部位的应力比和主应力引入到寿命预测模型中，提出了涡轮盘多轴疲劳寿命预测模型。Getsov等[7]采用有限元仿真技术分析了涡轮盘的热弹性变形，并基于热弹性粘塑性模型对涡轮盘疲劳寿命进行了预测。刘红彬等[8]针对涡轮盘高低周复合疲劳失效，以TC-11材料为研究对象展开了涡轮盘疲劳试验研究，得出复合循环比对涡轮盘复合寿命影响很小，并且在高低周应力载荷相差不大时，高周应力载荷起主要作用。赵振华等[9-10]以钛合金材料为样件对涡轮盘展开疲劳试验，得出涡轮盘高低周复合疲劳会造成涡轮盘抗疲劳性能降低。胡殿印等[11]针对涡轮盘研发出了一套高低周复合疲劳试验系统，以模拟涡轮盘关键部位的应力。姚伟等[12]采用正交基神经网络模型对涡轮盘展开了疲劳可靠性分析，得出神经网络模型对涡轮盘的疲劳可靠性问题具有更高的计算效率，而且计算精度也满足工程要求。

综上所述，目前对航空发动机涡轮盘已有很多研究成果，对涡轮盘的寿命及可靠性也有相关的分析方法及模型，但是针对航空发动机涡轮盘更加贴合实际工程的高精度可靠性模型仍然是目前学术界与工业界的研究热点。基于此，本文针对实际工程中涡轮盘的多源可靠性数据，引入模糊理论和层次贝叶斯方法，提出适用于航空发动机涡轮盘的疲劳可靠性分析方法，进一步丰富疲劳可靠性的内涵，为涡轮盘的可靠性分析提供一定的技术支撑。

1 不确定信息的测度及融合方法

1.1 层次贝叶斯方法

由前文所述，本文针对航空发动机涡轮盘不同来源的可靠性数据，联合层次贝叶斯方法和模糊理论对涡轮盘的疲劳可靠性问题展开研究。首先单独使用层次贝叶斯方法对不同来源的数据进行处理；其次通过贝叶斯推理获得相应的后验分布；最后采用信息融合方法得到涡轮盘精确的应力信息。

由贝叶斯理论可知：

针对现场样本数据＝(1,2, ...,x)和先验分布π()，可得到参数的后验分布为：

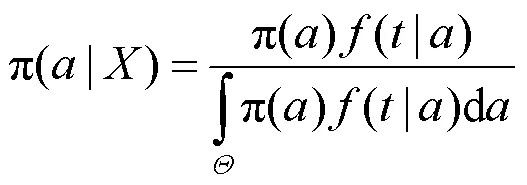
式中：为参数的取值范围。

1.2 模糊理论

由前文所述可知，航空发动机涡轮盘的疲劳可靠性研究中，其可靠性数据有多种来源，既包括涡轮盘疲劳失效的寿命数据，又包括涡轮盘的有限元仿真数据。而且，涡轮盘的现场疲劳失效寿命数据的可信度通常高于涡轮盘仿真数据的可信度。针对这一问题，本文利用模糊理论来对不同来源的涡轮盘可靠性数据的可信度进行量化表征。

假设两种不同来源的涡轮盘可靠性数据的

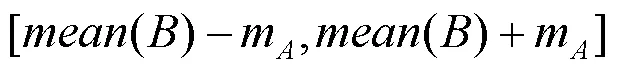
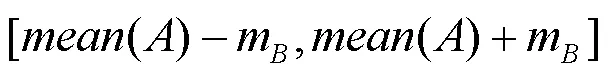
2 航空发动机涡轮盘有限元仿真

2.1 有限元建模及网格划分

本文采用ANSYS有限元仿真软件[14-15]对涡轮盘榫槽和螺栓孔的应力集中部位展开分析。航空发动机涡轮盘结构上有90个榫槽和6个螺栓孔，应力集中主要发生在榫槽和螺栓孔上，因而本文分别对榫槽和螺栓孔进行有限元仿真分析。在对涡轮盘上螺栓孔进行应力分析时，由于涡轮盘结构极具对称性，因而本文取涡轮盘1/6区域来进行仿真分析，如图1所示。同理，在对涡轮盘榫槽进行应力分析时，选取1/90区域来进行仿真分析，如图2所示。

图1 涡轮盘1/6区域

图2 涡轮盘1/90区域

这里需要特别指出的是，在对涡轮盘的三维结构模型进行网格划分时，应该针对涡轮盘应力应变实际情况，对涡轮盘榫槽和螺栓孔进行更为精密细致的网格划分，其他部分网格划分相对稀疏。

2.2 涡轮盘载荷与边界条件设置

本文考虑涡轮盘承受的温度载荷和离心力载荷对涡轮盘进行边界约束设置。在离心力载荷作用下对涡轮盘螺栓孔进行有限元仿真分析时，涡轮盘本身的离心力载荷采用转速的形式进行设置，涡轮盘叶片所产生的离心力载荷采用压强的形式进行设置。对于航空发动机1/6区域涡轮盘螺栓孔结构，涡轮盘叶片旋转所产生的压强为：

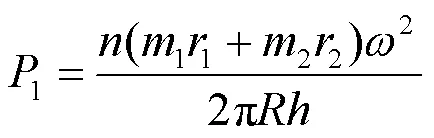
式中：1为压强，MPa；＝15为涡轮盘上安装的叶片数；1为榫槽结构上的叶片重量，kg；2为榫槽结构上的凸块重量，kg；1为涡轮盘叶片的质心半径，mm；2为榫槽结构的质心半径，mm；为涡轮盘的转速，rad·s-1；为涡轮盘的半径，mm；为涡轮盘外缘的轴向厚度，mm。

同理，在离心力载荷作用下对涡轮盘榫槽进行有限元仿真分析时，涡轮盘本身的离心力载荷采用转速的形式进行设置，涡轮盘叶片所产生的离心力载荷采用压强的形式进行设置。这里需要指出的是，对于航空发动机1/90区域涡轮盘榫槽结构而言，涡轮盘叶片旋转所产生的压强为：

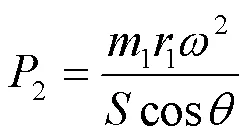
式中：2为压强，MPa；为榫槽结构上离心力与受力齿面的夹角，rad；为榫槽结构受力齿面总面积，mm2。

涡轮盘在最大稳态和慢车稳态的不同工况下，由于涡轮盘的转速不同，导致叶片作用在涡轮盘榫槽和端面上的压强往往不同，表1和表2分别为涡轮盘1/6区域和1/90区域所对应的压强。

表1 涡轮盘1/6区域结构端面上所受应力

表2 涡轮盘1/90区域结构榫槽部位的应力

航空发动机涡轮盘通常在高温环境下工作，因而在对涡轮盘进行应力分析时，不能忽略温度载荷的作用。依据在笛卡尔坐标系下涡轮盘的温度载荷数据，将涡轮盘温度载荷数据以表格的形式在ANSYS软件中进行设置，并将其施加到涡轮盘结构的各个部位上。

总之，在采用ANSYS软件对涡轮盘进行有限元分析时，在涡轮盘结构上设置的边界约束如下：

（1）针对图1所示的涡轮盘1/6区域：对涡轮盘螺栓孔端面设置轴向的位移约束和周向的位移约束，同时对涡轮盘两侧设置对称约束，如图3所示。

（2）针对图2所示的涡轮盘1/90区域需要设置轴向的位移约束和周向的位移约束，同时对涡轮盘两侧设置对称约束。

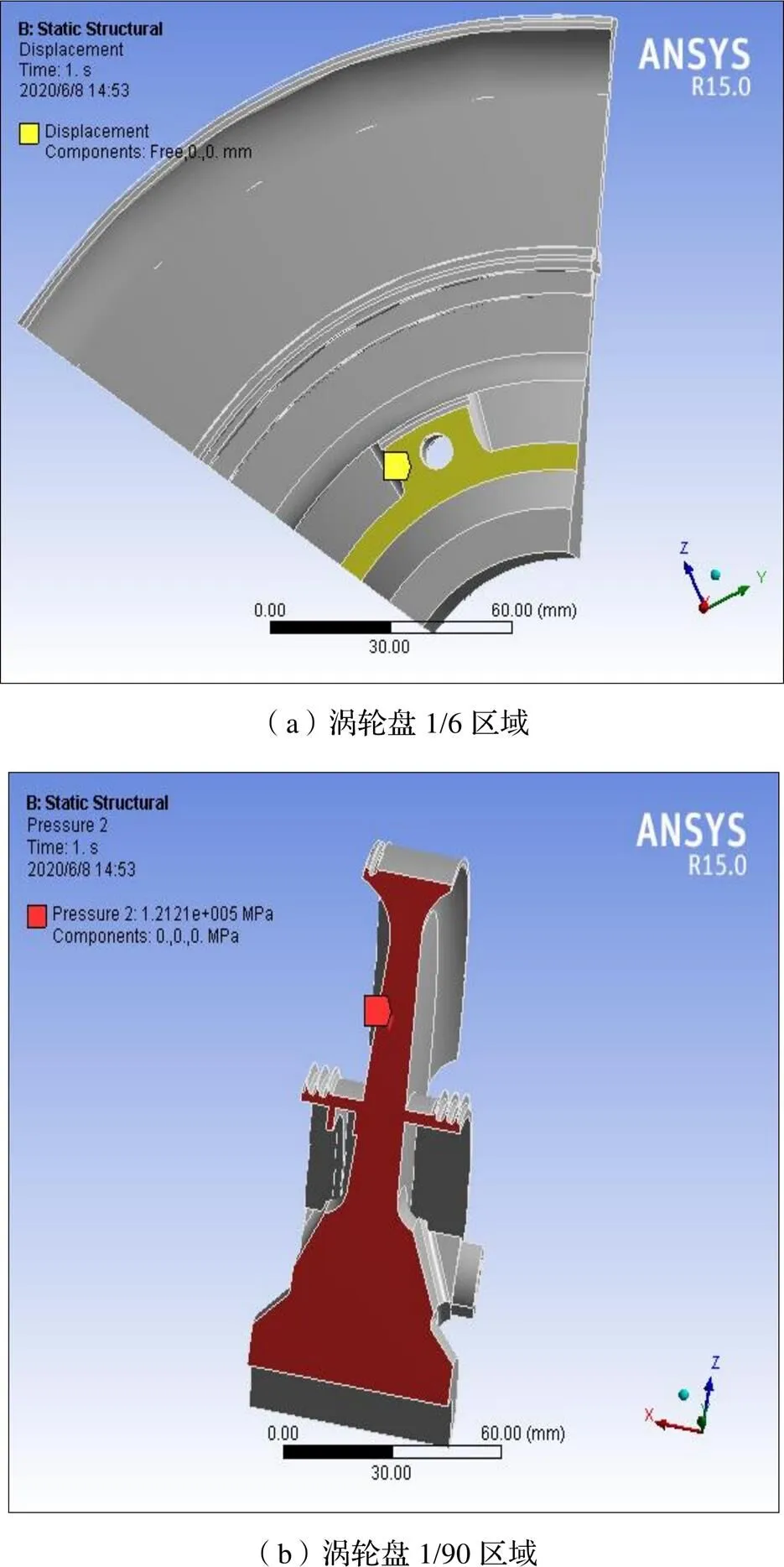
图3 涡轮盘结构上的边界约束

2.3 涡轮盘应力应变分析结果

由前文所述可知，针对图1和图2中的涡轮盘区域进行有限元仿真时，需添加温度载荷和离心力载荷，在“最大”工况下涡轮盘的应力应变结果如图4～6所示。

由图4～6的涡轮盘有限元分析结果可知，涡轮盘在螺栓孔、中心孔和榫槽处应力集中最大，因而在对涡轮盘进行疲劳可靠性分析及寿命预测时，这三处薄弱环节应重点考虑。同时，在涡轮盘“最大”“巡航”和“慢车”三种工况下涡轮盘薄弱环节处的最大等效应力应变仿真结果如表3～5所示。

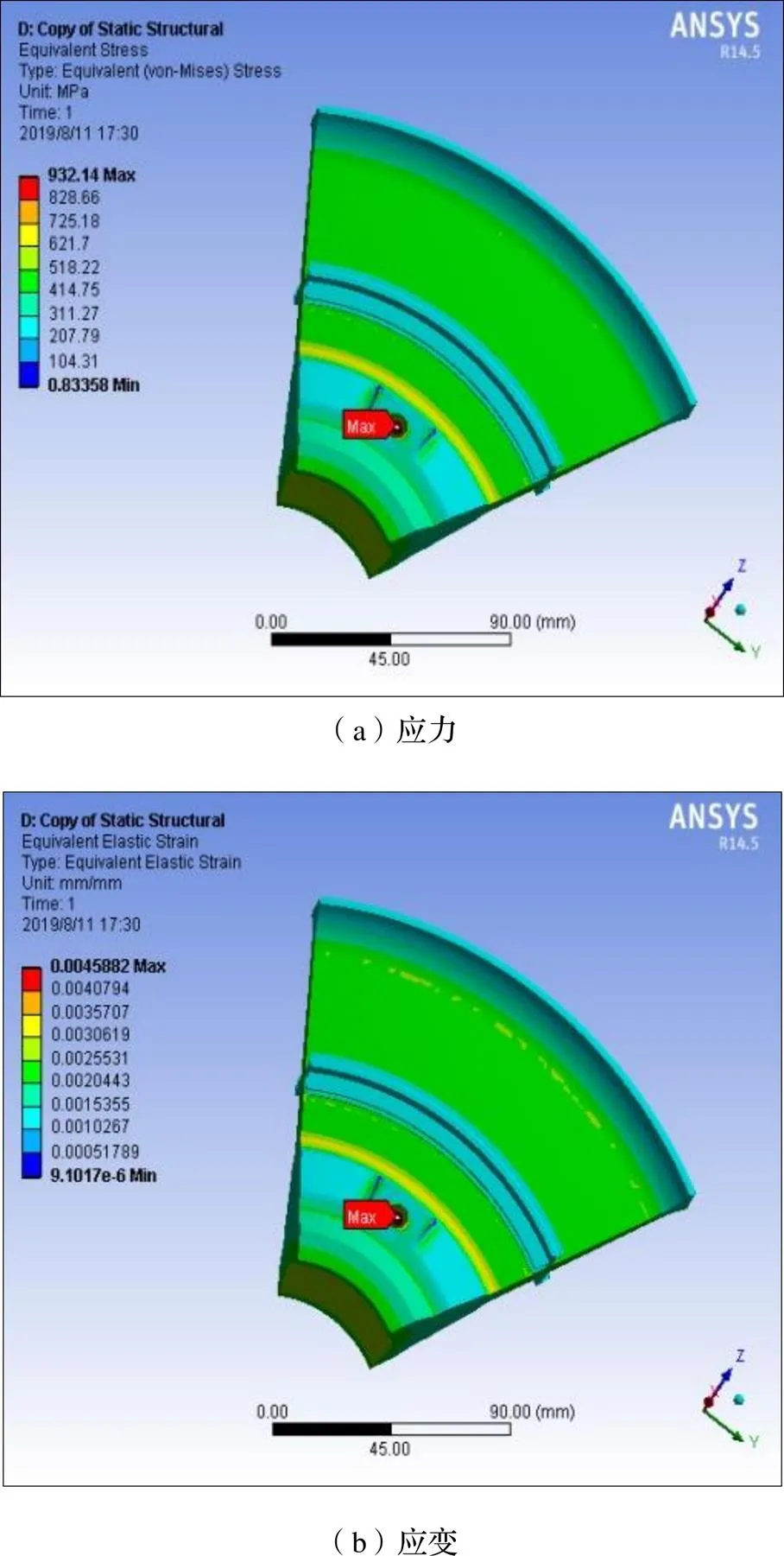
图4 1/6涡轮盘区域结构螺栓孔处的应力和应变

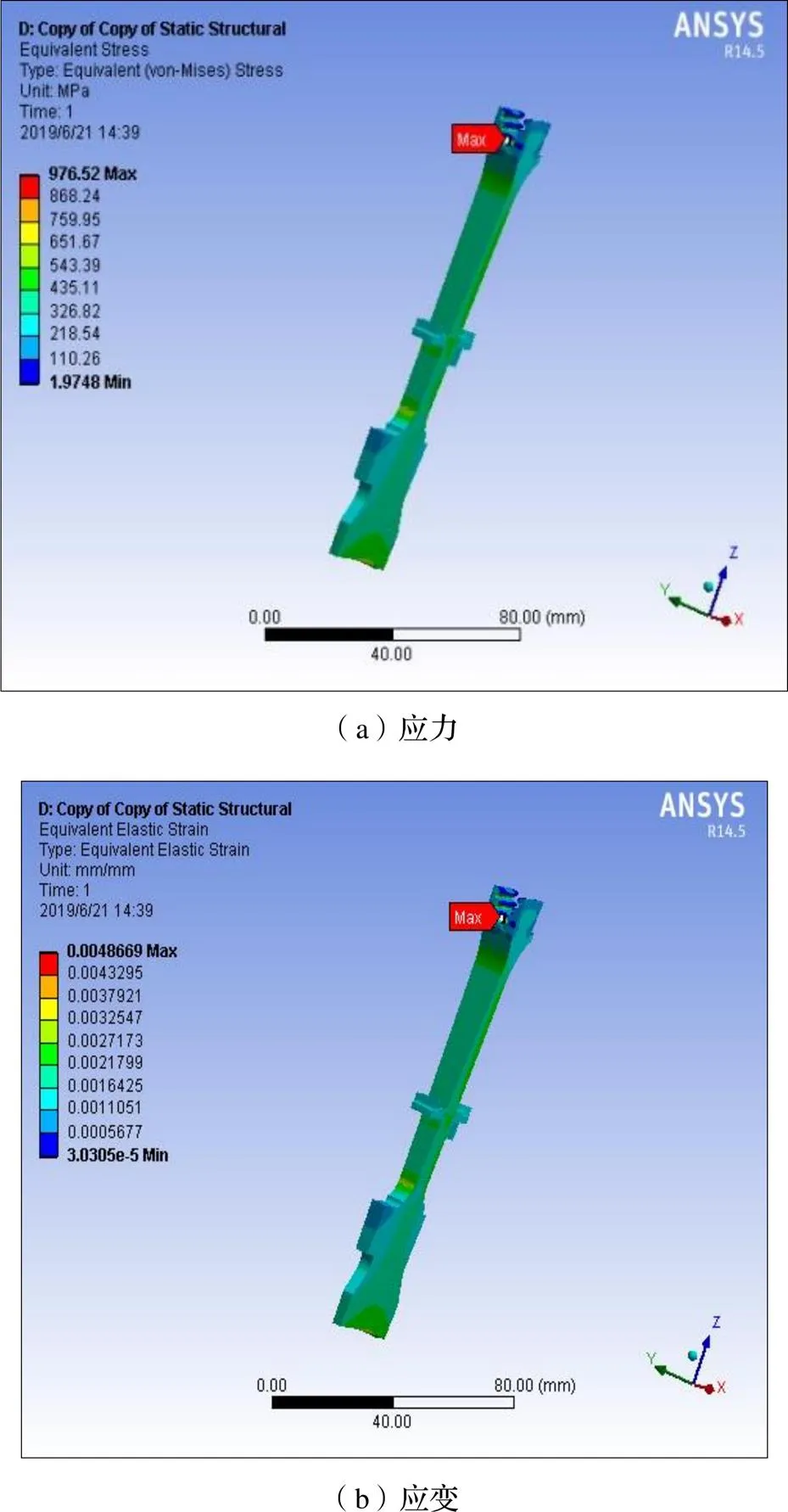
图5 1/90涡轮盘区域结构榫槽处的应力和应变

本文采用拉丁超立方抽样技术对涡轮盘的转速进行取样，并使用ANSYS仿真软件对温度载荷作用下涡轮盘的应力进行仿真，进一步得到不同转速下涡轮盘薄弱环节处的最大等效应力值，仿真得到的涡轮盘等效应力数据如表6所示。

对表6中涡轮盘仿真数据开展分布假设检验，拟合出的结果如图7所示，其表明该涡轮盘螺栓孔处的仿真应力数据近似服从正态分布，即Normal(799.8460, 1116.3)。进一步得到仿真的涡轮盘薄弱环节的应力数据的先验分布π1(|)。

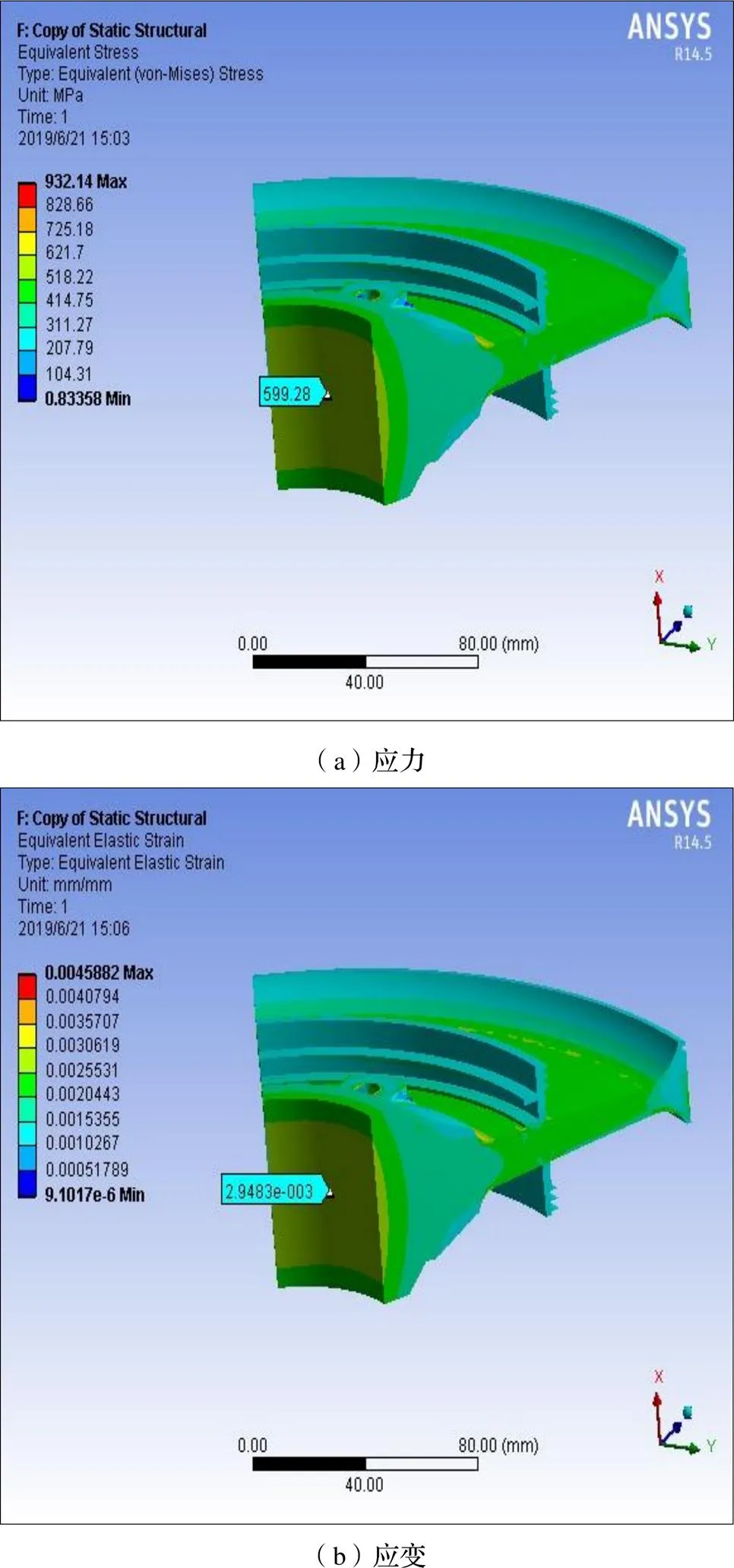
图6 1/6涡轮盘区域结构中心孔处的应力和应变

表3 涡轮盘1/6区域榫槽处最大等效应力应变

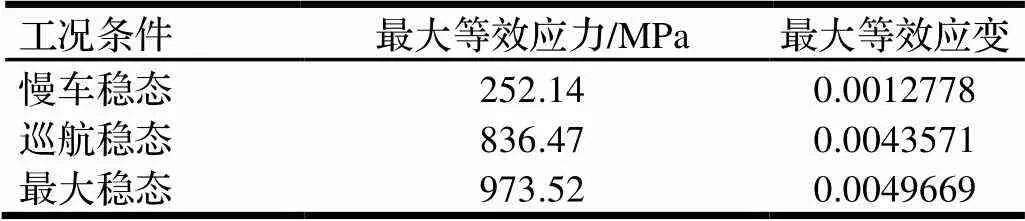
表4 涡轮盘1/90区域螺栓孔最大等效应力应变

表5 涡轮盘1/6区域中心孔最大等效应力应变

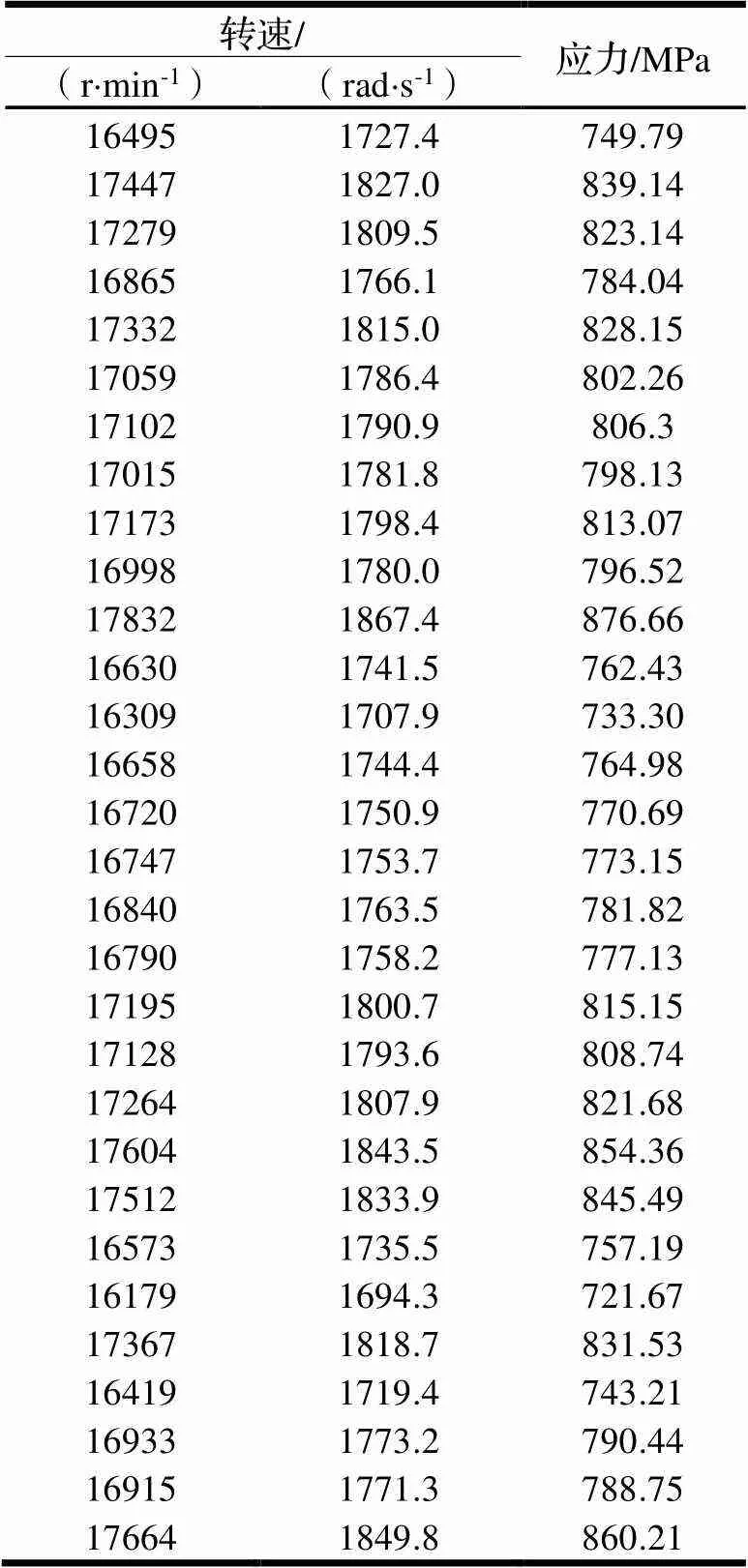
表6 涡轮盘螺栓孔处的应力仿真值

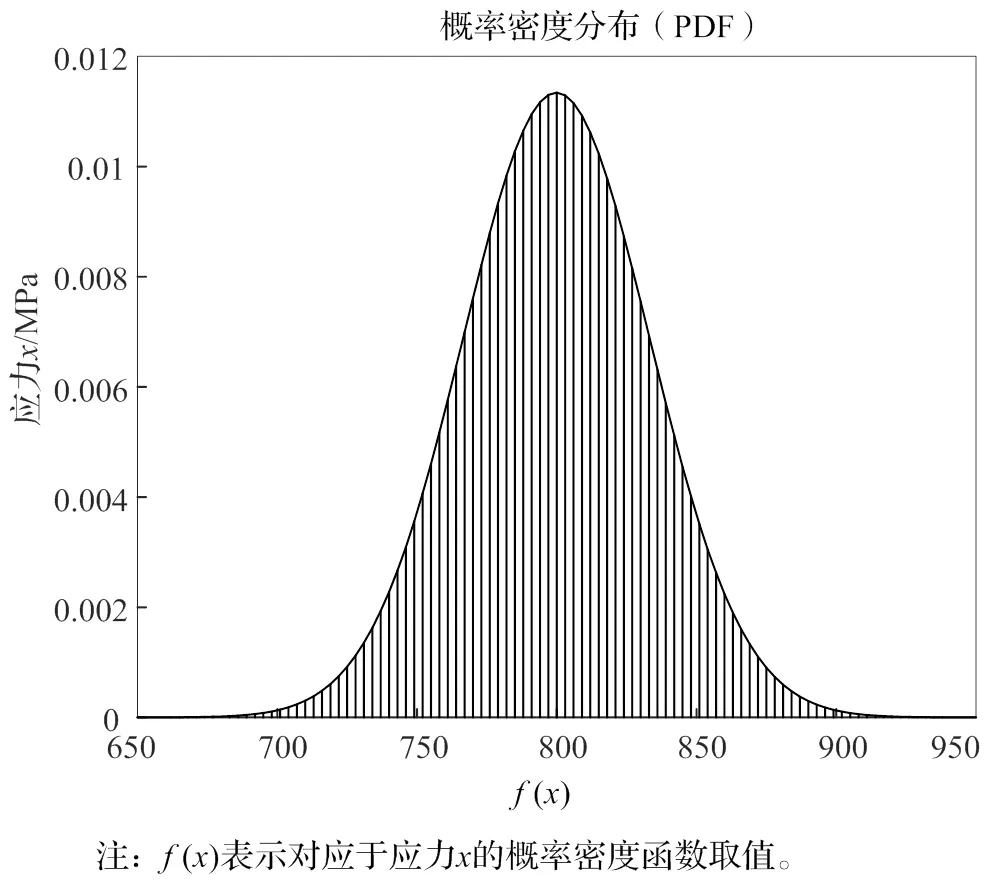
图7 涡轮盘仿真应力数据分布假设检验

3 航空发动机涡轮盘疲劳可靠性分析

在不同工况下航空发动机涡轮盘运行800 h时的载荷情况如表7所示。

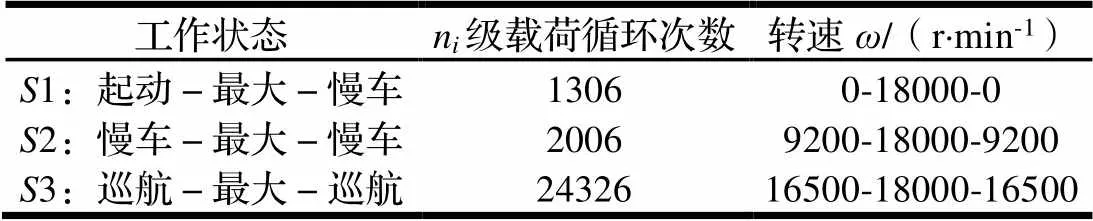
表7 涡轮盘运行800 h时的载荷谱

由前文可知，涡轮盘的可靠性数据有着多源的特点，而且涡轮盘的结构尺寸、材料属性和模型参数等都存在着一定的不确定性，针对这一情况，本文采用层次贝叶斯方法和模糊理论对涡轮盘的疲劳可靠性问题展开分析。

3.1 基于模糊理论与层次贝叶斯方法的应力信息融合

本文以GH413材料为研究对象展开涡轮盘的疲劳可靠性研究，并基于该涡轮盘的现场疲劳失效寿命数据，采用OpenBUGS贝叶斯分析软件获得该涡轮盘薄弱环节处的应力先验分布参数。分析结果如图8所示，其中，基于现场失效数据的涡轮盘应力先验分布服从Normal(765.09, 191.18)，即得到现场失效数据下涡轮盘薄弱环节处的应力数据的先验分布π2(|)。

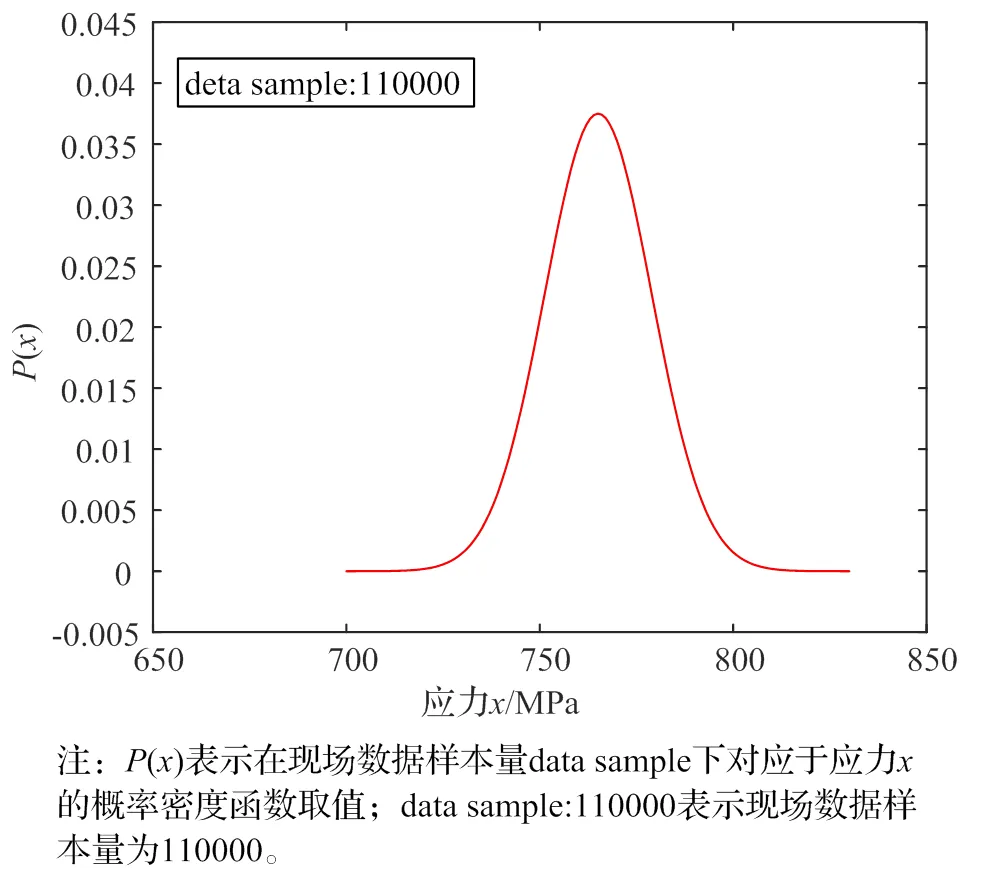
图8 现场失效数据下涡轮盘应力先验分布

本文假设由仿真得到的涡轮盘薄弱环节处的应力先验分布π1(|)的置信区间为[0.45, 0.89]，并且由现场失效数据得到的涡轮盘薄弱环节处的应力先验分布π2(|)的置信区间为[0.34, 0.78]，从而可得到δ＝0.67且δ＝0.56，即δ＞δ。进一步采用模糊理论对上述涡轮盘的两种不同来源的可靠性数据信息展开融合，可得在最大转速下涡轮盘薄弱环节处的应力分布为：

～([749.2661, 780.913], 3569) （7）

3.2 基于复杂载荷作用的强度退化分析

本文采用文献[16]提出的强度退化模型来描述CH4133材料下涡轮盘结构在多级载荷作用下的剩余强度：

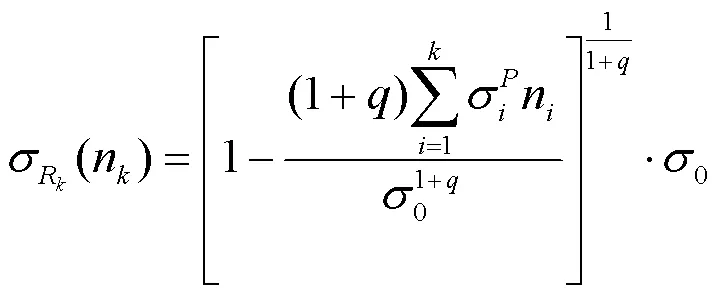
本文所述航空发动机涡轮盘的初始强度为～(1180, 592)。基于表7中涡轮盘运行800 h的载荷情况，可以得到涡轮盘在载荷1＝1306和2＝2006下的二级应力水平，进一步可以得到涡轮盘在每个应力等幅作用多次下的剩余强度均值为963.21 MPa。

3.3 涡轮盘疲劳可靠性计算

在航空发动机实际运行过程中，通常会伴随着飞机经历启动－最大－启动、巡航－最大－巡航和慢车－最大－慢车三种工况环境，同时涡轮盘也会相应地经历不同的工况环境。其中，巡航－最大－巡航工况下涡轮盘承受的循环载荷次数远大于107，此阶段可以把涡轮盘视为无限寿命。因此，本文只针对另外两种工况下涡轮盘的疲劳可靠性问题展开研究，在该两种工况下，涡轮盘都会经历一定的载荷循环次数，其疲劳可靠性为：

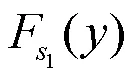
另外，涡轮盘在该两种工况下循环载荷作用次数满足如下比例关系：

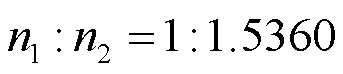
由前文可知，在最大转速下航空发动机涡轮盘薄弱环节处的最大应力分布为～（[749.2661, 780.913], 3569），本文取其上下界来对涡轮盘的疲劳可靠性展开计算。而且，假定该涡轮盘的强度服从正态分布，即～（963.21, 2652.3），进一步可计算出该涡轮盘的疲劳可靠度。基于本文提出的方法，可以得到涡轮盘薄弱环节处最大应力均值的上下界分别为：

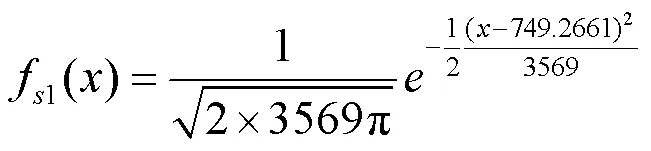
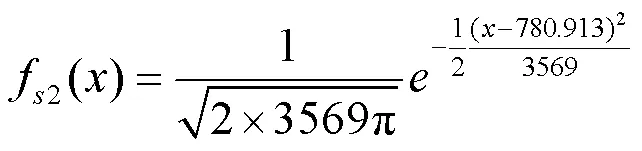
将式（13）代入式（11）中可得到涡轮盘高边界的疲劳可靠性，将式（14）代入式（11）中得到涡轮盘低边界的疲劳可靠性。针对涡轮盘载荷情况1＝1306和2＝2006，本文计算得到的航空发动机涡轮盘的疲劳可靠性为＝[0.7437, 0.8895]，即涡轮盘的真实疲劳可靠性在上述区间内波动。

本文假定在涡轮盘的载荷情况如表7所示时，飞行总时间和循环载荷作用次数的关系为：

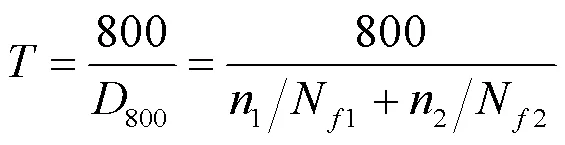
式中：为飞行总时间，h。

由前文所述得，在涡轮盘循环载荷作用次数1和2满足特定比例关系时，涡轮盘疲劳可靠度随着作用次数的变化规律如图9所示，并结合式（15），涡轮盘疲劳可靠性随着总飞行时间的变化规律如图10所示。

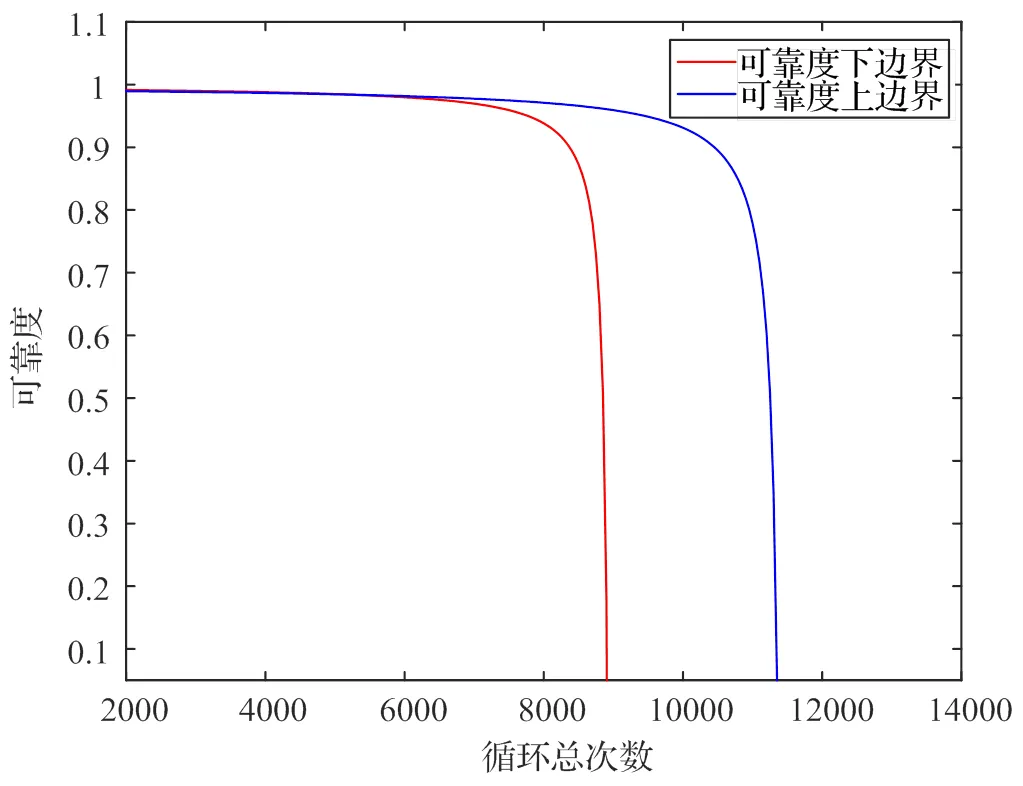
图9 可靠度上下边界随循环总次数的变化

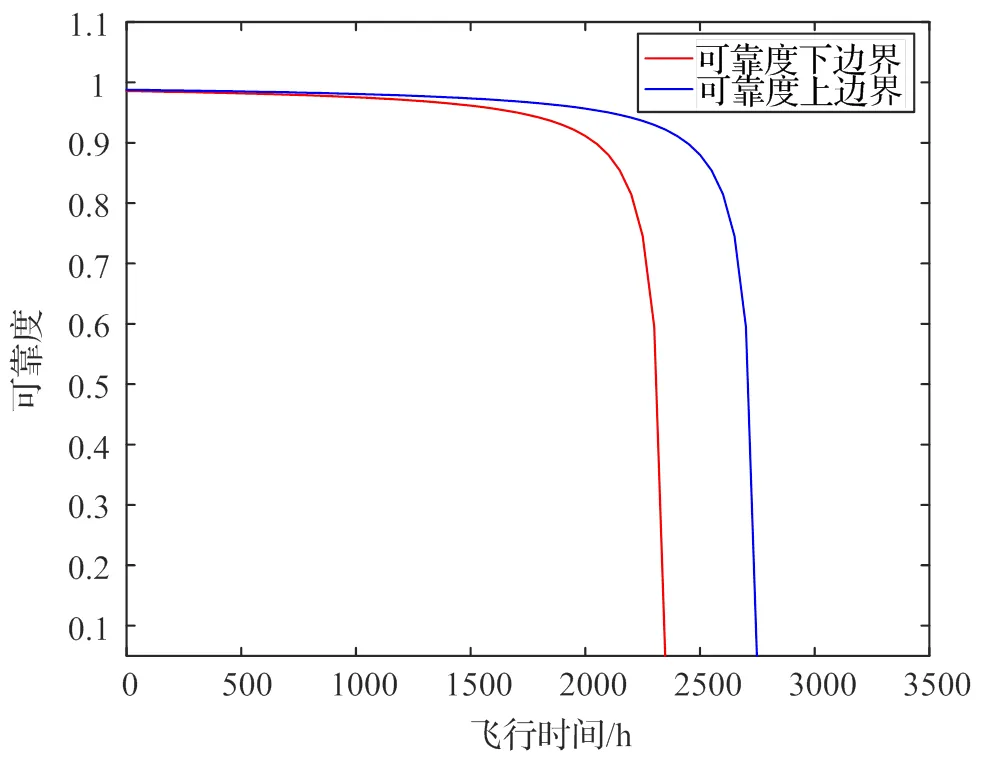
图10 可靠度上下边界随飞行总时间的变化

4 结论

本文针对航空发动机涡轮盘不同来源的可靠性数据，提出了联合模糊理论和层次贝叶斯方法的涡轮盘疲劳可靠性分析方法。针对GH413材料下的涡轮盘，基于该涡轮盘的现场失效数据和仿真数据，得到该涡轮盘的疲劳可靠性范围为＝[0.7437, 0.8895]。进一步比较保守地评估出该涡轮盘的疲劳寿命约为8000次，总飞行时间约为2000 h，为该航空发动机涡轮盘在实际工程中的维护及更新提供了参考。

[1]K. Tanaka. Engineering formulae for fatigue strength reduction due to crack-like notches[J]. International Journal of Fracture，1983，22（2）：39-46.

[2]D. Taylor. Geometrical effects in fatigue：a unifying theoretical model[J]. International Journal of Fatigue，1999，21（5）：413-420.

[3]R. A. Cláudio，C. M. Branco，E. C. Gomes，et al. Life prediction of a gas turbine disc using the finite element method[C]. Eighth Portuguese Conference on Fracture，2002.

[4]C. Ayyappan，R. Kumar，P. Ramesh，et al. Experimental and numerical study to predict residual growth in an aeroengine compressor disc after overspeed[J]. Procedia Engineering，2013（55）：625-630.

[5]L. Witek. Numerical simulation of fatigue fracture of the turbine disc[J]. Fatigue of Aircraft Structures，2012，12（4）：114-122.

[6]M. N. Menon，P. T. Kantzos，D. J. Greving. An innovative procedure for establishing lifing criteria for turbine disc bores under multiaxial states of stress[J]. International Journal of Fatigue，2011，33（8）：1111-1117.

[7]L. B. Getsov，A. S. Semenov，I. A. Ignatovich. Thermal fatigue analysis of turbine discs on the base of deformation criterion[J]. International Journal of Fatigue，2017（97）：88-97.

[8]刘红彬，黄维娜，陈伟. 合金材料高低周复合疲劳寿命研究[J]. 航空动力学报，2014，29（1）：74-80.

[9]赵振华，陈伟，吴铁鹰，等. 高低周复合载荷下的钛合金疲劳寿命估算[J]. 机械强度，2011，33（4）：629-632.

[10]赵振华，陈伟. 高低周复合载荷对TC11钛合金疲劳性能的影响[J]. 航空动力学报，2011，26（11）：2468-2474.

[11]胡殿印，魏佳明，王荣桥，等. 一种试验件高温高低周复合疲劳裂纹扩展试验系统及测量方法[P]. 中国发明专利，2015：CN201410853812. 0.

[12]姚伟，白广忱. 基于Fourier正交基神经网络的涡轮盘低循环疲劳可靠性分析[J]. 装备制造技术，2014（10）：132-134.

[13]H. Li，H. Z. Huang，Y. F. Li，et al. Physics of failure-based reliability prediction of turbine blades using multi-source information fusion[J]. Applied Soft Computing，2018（72）：624-635.

[14]赵晓琪，杨启志，赫明胜，等. 基于ANSYS Workbench的插接式管塔抗震性能分析[J]. 机械，2020，47（11）：1-7.

[15]何临江. 基于有限元分析的电工纯铁DT4E材料冲裁加工工艺研究[J]. 机械，2020，47（11）：63-70.

[16]张晓颖. 航空发动机涡轮盘的寿命与可靠性分析[D]. 成都：电子科技大学，2020.

Fatigue Reliability Analysis of Turbine Disk Based on Fuzzy Theory and Hierarchical Bayesian Method

GAN Qiyi1，HUANG Hongzhong2，ZHANG Xiaoying2，LI Yanfeng2，QIAN Huaming2

(1.Chengdu Hi-Tech Entrepreneurship Service Center, Chengdu 610041, China;2.School of Mechanical and Electrical Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China)

The reliability data of aero-engine turbine disk are usually from multiple sources and the credibility of each data source is also different, which brings serious challenges for reliability analysis of turbine disk. In order to solve this problem, this paper applied the hierarchical Bayesian method to fuse the observation data with other multi-source prior information. Then the reliability data of turbine disk from different sources are analyzed by Bayesian inference to obtain the posterior distributions. Finally, the fuzzy theory is used to analyze the posterior distribution of the multi-source information, thus an analysis method of the turbine disk fatigue reliability was developed with a combination of fuzzy theory and hierarchical Bayesian method. The proposed method is applied to the fatigue reliability analysis of an aero-engine turbine disk to verify its effectiveness.

aero-engine；turbine disk；fuzzy theory；hierarchical Bayesian；fatigue reliability

V232.3

A

10.3969/j.issn.1006-0316.2021.08.002

1006-0316 (2021) 08-0007-09

2021-03-07

国家科技重大专项（2017-IV-0009-0046）

甘启义（1963－），男，四川内江人，博士，主要研究方向为机电一体化、科研开发和管理等，E-mail：1228945849@qq.com。

通讯作者：黄洪钟（1963－），男，重庆人，博士，教授，主要研究方向为可靠性、寿命预测、智能优化等，E-mail：hzhuang@uestc.edu.cn。