基于层次多尺度散布熵的滚动轴承智能故障诊断
2021-09-04鄢小安贾民平
鄢小安,贾民平
(1.南京林业大学机械电子工程学院,南京 210037; 2.东南大学机械工程学院,南京 211189)
0 引 言
滚动轴承作为机械设备重要的组成部件,在航空航天、高速铁路、矿山冶金、风力发电等行业都是必不可少的[1]。在实际工程应用中,随着机械设备的长期运转,受载荷、转速、环境等多因素影响,轴承会不可避免地出现损坏,其故障发展过程通常会经历正常、轻微故障、中度故障、严重故障、失效等几个阶段。然而,滚动轴承在整个生命周期内的运行健康状态不易有效辨识和区分。因此,如何采用先进的特征提取方法从轴承全寿命周期数据内获取有效丰富的故障诊断信息,对保障机械设备安全稳定运行具有重要的现实意义[2]。
近些年,研究学者提出许多非线性动力学方法用于评估信号的复杂性与不确定性,如谱熵、样本熵、排列熵[3]、模糊熵、符号动力学熵[4]等。以上方法在机械故障诊断领域得到了很好的应用。孙鲜明等[5]提出一种瞬时包络尺度谱熵,有效提取了轴承故障信息,并对轴承早期故障异常点进行了准确识别。冯辅周等[6]采用一种小波相关排列熵对轴承早期故障进行了有效识别。李永波等[7]提出一种层次模糊熵(Hierarchical Fuzzy Entropy, HFE)获取轴承故障特征信息,并结合二叉树支持向量机准确地识别了轴承不同故障类型及程度。Wu等[8]结合多尺度排列熵(Multiscale Permutation Entropy, MPE)和支持向量机有效地识别了轴承故障类型。Zhu等[9]采用层次样本熵(Hierarchical Sample Entropy, HSE)提取轴承故障特征,并结合基于粒子群优化的支持向量机对轴承故障模式进行了有效辨识。Zheng等[10]将广义复合多尺度排列熵(Generalized Composite Multiscale Permutation Entropy,GCMPE)与拉普拉斯分值特征选择相结合对轴承故障模式进行了有效检测。Wang等[11]首先采用一种广义精细复合多尺度样本熵(Generalized Refined Composite Multiscale Sample Entropy, GRCMSE)获取轴承故障特征信息,然后将提取的故障特征输入到支持向量机中进行了有效识别。然而,上述方法仅在原信号多尺度或多层次上挖掘轴承故障信息,没有同时兼顾信号不同层次及不同频段上的多尺度故障特征。换言之,上述方法所获取的故障信息不够全面、丰富。因此,为解决上述方法中存在的问题,Yang等[12]将层次多尺度排列熵(Hierarchical Multiscale Permutation Entropy, HMPE)和模糊支持张量机相结合,对不同的轴承故障类型进行了有效识别。另外,散布熵(Dispersion Entropy, DE)作为一种新的信号复杂性评价指标[13-15],与现有的排列熵(Permutation Entropy, PE)、模糊熵(Fuzzy Entropy, FE)和样本熵(Sample Entropy, SE)相比,具有运行速度快、计算效率高的优点。当时间序列的数据长度较小时,散布熵不会出现没有定义的熵值,并且很好地考虑到了信号幅值的重要信息。因此,在散布熵优点的基础上,Zhou等[16]提出了一种修改的层次多尺度散布熵(Modified Hierarchical Multiscale Dispersion Entropy, MHMDE),并结合核极限学习机对旋转机械关键部件(如轴承、齿轮)进行了有效的故障识别。然而,文献[12]和[16]的方法是依靠人为经验选取熵值的重要参数,不具备自适应性,而且容易影响故障特征提取性能。
同时,在故障信息获取后需要进行智能识别。为此,许多线性或非线性向量分类模型被依次提出,包括线性判别分析(Linear Discriminant Analysis, LDA)、人工神经网络(Artificial Neural Network, ANN)、极限学习机(Extreme Learning Machine, ELM)和支持向量机(Support Vector Machine, SVM)等,其中SVM因其算法简单、鲁棒性好在智能诊断领域受到了极大关注。然而,SVM在应用过程中需要将矩阵形式的特征信息转换成向量形式,这容易引起原振动信号内部结构信息丢失,从而降低分类性能。因此,为克服这一问题,Luo等[17]在2015年提出一种新型非线性分类模型——支持矩阵机(Support Matrix Machine, SMM)。与传统SVM相比,SMM可以直接从原始特征矩阵中学习其内部结构信息,具有更强的小样本特征学习性能和鲁棒性。迄今为止,SMM已成功应用在脑电图分类中,但其在轴承健康状态识别中的应用报道较少。
综上,本文结合层次分解、多尺度粗粒化分析和鸟群优化算法提出一种基于层次多尺度散布熵(Hierarchical Multiscale Dispersion Entropy, HMDE)的轴承智能诊断方法。采用参数自适应优化的HMDE提取矩阵形式的轴承故障特征信息,将提取的多维故障特征矩阵输入SMM进行模型训练并完成轴承健康状态的自动识别。通过两组轴承加速寿命实验数据的分析,以验证提出方法在识别轴承故障模式与故障程度方面的有效性。
1 层次多尺度散布熵
1.1 HMDE的定义
图1为HMDE的流程图。对于一个给定的时间序列{x(i),i= 1 ,2,… ,N},HMDE的计算过程如下:
1)定义一个平均算子Q0和差分算子Q1为[18]
式中 2n-1为算子的长度,n为正整数,Q0(x)和Q1(x)分别表示原始时间序列在第一层分解中的低频成分和高频成分。
2)为了描述信号的层次分析,当j=0或1时,定义第k层算子的矩阵形式为[19]
3)为了获得层次分解过程中各层的层次分量Xk,e,需要反复使用上述定义的Qkj算子,同时需要定义一个一维向量[γ1,γ2,… ,γk]和一个整数值,其中{γp,p= 1 ,2,… ,k} ∊ { 0,1}表示第p层的平均或差分算子。据此,第k层的第e个节点的层次分量可表示为[20]
4)根据公式(5)计算各层次分量Xk,e在τ尺度下的复合粗粒化序列
式中DE(·)为散布熵运算,m为嵌入维数,c为类别个数,d为时间延迟(s),k为分解层数,e为节点,τ为尺度因子。
1.2 参数影响研究
为了考察不同参数对HMDE性能的影响,对美国凯斯西储大学(Case Western Reserve University, CWRU)公开的基准数据集[21]进行分析。试验装置由驱动电机、轴承座、转矩传感器和测力计等组成,如图2所示,驱动端轴承为 SKF6205,风扇端轴承为 SKF6203。试验过程中,采样频率为12 kHz,采样长度为4 096点,在电机驱动端轴承座上安装一个加速度传感器分别采集 1组轴承正常加速度数据和1组轴承外圈故障数据。限于篇幅,表1仅列出了不同参数下轴承正常信号的前2行4列的层次多尺度散布熵。

表1 不同参数下轴承正常信号的层次多尺度散布熵Table 1 HMDE of bearing normal signal under different parameters
从表1可以看出,当其他参数固定、嵌入维数m增加时,各层次或尺度下的散布熵值会出现一定增长。当其他参数固定、时间延迟d增加时,各层次或尺度下的散布熵值也会出现变化,但变化程度不明显。当其他参数固定、类别个数c增加时,各层次或尺度下的散布熵值会发生较明显变化。此外,当其他参数固定、分解层数k和尺度因子τ增加时,可以获取更丰富、全面的散布熵特征,但也增加了相应的计算量。由于外圈故障信号的HMDE的变化规律与表1基本一致,这里不再重复赘述。因此,通过上述分析可以得出,时间延迟d对HMDE的计算结果影响较小,而其他4个参数(即嵌入维数m、类别个数c、分解层数k和尺度因子τ)对计算结果具有较大影响。
为了分析HMDE对轴承故障特征提取的有效性,将其与现有的7种复杂性度量方法进行对比分析。这7种对比方法分别为精细复合多尺度散布熵(Refined Composite Multiscale Dispersion Entropy, RCMDE)[22]、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE。具体地,分别采用HMDE和7种对比方法计算上述轴承正常数据和外圈故障数据的熵值变化情况,并计算两者之间的欧式距离(Euclidean Distance, ED),进而对比不同方法的轴承故障特征提取性能。需要注意的是,各算法中的参数均设置为嵌入维数m=3,时间延迟d=1 s,类别个数c=5,尺度因子τ=8,分解层数k=3,相似容限r=0.15σ,其中σ为原信号的标准差。限于篇幅,表2仅列出了不同方法下轴承正常信号的前1行4列的熵值。表3列出了各算法5次试验的平均欧式距离ED和平均运行时间。从表3可看出,相比其他方法,HMDE的平均欧式距离最大,说明HMDE获得的特征信息更具区分性,具备更优越的信号复杂性评估性能。此外,就各算法的平均运行速度而言,HMDE的运行时间与MHMDE比较接近,同时明显小于GRCMSE、HFE、HSE和HMPE的运行时间,但大于RCMDE和GCMPE的运行时间,这主要是由于 HMDE中集成了层次分解和多尺度分析过程,因此引起了计算效率的下降。
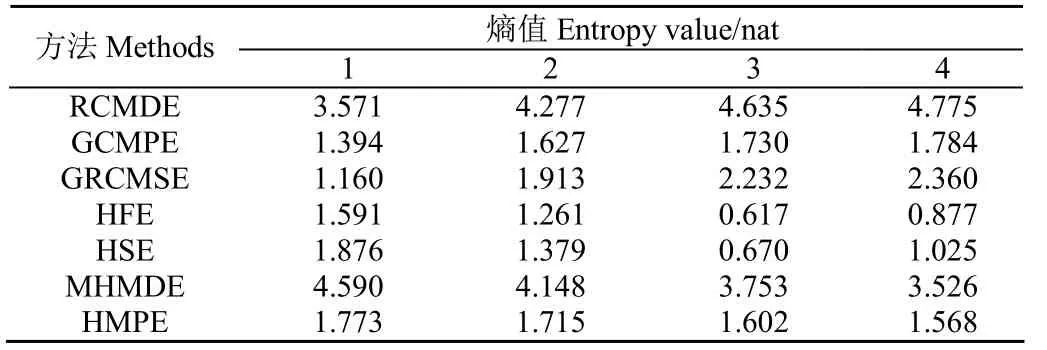
表2 不同方法下轴承正常信号的熵值Table 2 Entropy value of bearing normal signal with different methods

表3 不同方法的平均欧式距离和平均运行时间Table 3 Average Euclidean distance and average run time of different methods
1.3 参数优化
目前,群智能寻优算法在解决参数优化问题方面卓有成效,包括常见的粒子群优化(Particle Swarm Optimization, PSO)、蚁群算法(Ant Colony Algorithm,ACO)、蝙蝠算法(Bat Algorithm, BA)等。鸟群优化算法(Bird Swarm Algorithm, BSA)是Meng等[23]在2016年提出的一种新型仿生寻优算法。与其他寻优算法相比,BSA在参数优化方面具有优化精度高、稳定性强、收敛速度快等优点。为此,综合考虑各参数之间的交互作用,本文采用BSA对HMDE的4个重要参数(即嵌入维数m、类别个数c、分解层数k和尺度因子τ)进行自适应选取。参数优化过程概括如下:
1)初始化种群和设置 BSA的各项参数。当迭代数t=0时,设置鸟群规模N=20,最大迭代数M=30,初始化飞行频率FQ,觅食频率P和几个常量(即认知加速系数C,社会加速系数S,0~2之间的正整数FL、正数a1和正数a2)。
2)计算适应度值。根据式(7)所示的适应度函数计算并比较鸟群的适应度值,确定鸟群个体最佳位置和鸟群整体最佳位置。
式中xi为错误分类样本数,xc为正确分类样本数,fitness(i)为第i只鸟的当前适应度值。当fitness(i)取到最大值时,对应的鸟群个体最佳位置为pi,j,同时对应的鸟群整体最佳位置为gj。
3)通过判断飞行频率FQ与迭代数t相乘再除以100的运算t×FQ/100是否存在余数,执行迭代运算并确定位置更新公式。具体如下:
若t×FQ/100存在余数,则随机生成一个均匀分布数。当随机数小于觅食频率P时,鸟群个体将执行觅食行为,位置更新公式如式(8);当随机数大于或等于觅食频率P时,鸟群个体保持警戒行为,位置更新公式如式(9)。
式中rand(0,1)为0到1之间的一个均匀分布随机数。
若t×FQ/100不存在余数,当鸟群个体为生产者时,位置更新公式如式(10);当鸟群个体为乞讨者时,位置更新公式如(11)。
式中 randn是一种产生随机数或矩阵的函数,randn(0,1)表示生成均值为 0、标准差为 1的高斯分布随机数,k∊[1,2,3,… ,N],k≠i。
4)根据步骤3)的准则,更新每个鸟群个体的位置。若当前鸟群个体位置好于先前鸟群个体位置,则当前鸟群个体位置被当作最优位置。否则,保留先前鸟群个体位置为最优位置继续鸟群更新。
5)判断是否满足停止条件。若达到最大迭代次数或最小错分率,则整个优化过程结束,输出鸟群的最优位置(即HMDE的最优组合参数)。否则,继续循环迭代直到满足停止条件。
2 基于HMDE的轴承智能诊断方法
为了获取更丰富、更全面的轴承故障特征信息,同时提高故障诊断精度,本文提出一种基于HMDE的轴承智能故障诊断方法。图3为提出方法的流程图,其具体实现过程表述如下:
1)通过在试验设备上安装加速度传感器,获取全寿命周期内的轴承振动数据。
2)通过鸟群优化算法自适应确定 HMDE的最优参数,并根据最优参数计算不同健康状态下轴承振动数据的HMDE作为多维度特征矩阵。
3)将多维度特征矩阵随机划分为训练样本矩阵和测试样本矩阵,采用训练样本矩阵对SMM进行模型训练,并将测试样本矩阵输入到训练好的 SMM 模型中进行测试和自动输出识别结果。在该步骤中,假设给定的训练数据集为为第i个输入矩阵,yi∊ { 1,-1 }为训练标签,d1和d2分别表示输入矩阵的行数和列数,则SMM可以通过合页损失函数和谱弹性网络惩罚函数来实现模型的训练和分类,如下所示:
3 试验验证
本文通过轴承故障诊断试验来验证所提方法的故障特征提取与智能诊断能力。试验采用 2组轴承加速寿命数据集:西安交通大学与昇阳科技的XJTU-SY轴承加速寿命试验数据[24]、东南大学状态监测与故障诊断研究中心的ABLT-1A轴承加速寿命试验数据。
3.1 设备与方法
XJTU-SY轴承加速寿命试验数据源自西安交通大学与浙江长兴昇阳科技有限公司的机械装备健康监测联合实验室。图4所示试验台主要由数字式力显示器、电机转速控制器、交流电机、支撑轴承和液压加载系统等部分组成。在试验过程中,将2个PCB-352C33加速度计分别安装在测试轴承的垂直和水平方向,采用DT9837便携式动态信号采集器对轴承全寿命数据进行了监测与记录。测试轴承型号为UER204,滚动体直径为7.92 mm,节圆直径为34.55 mm,滚动体数量为8个,接触角为0°。数据采集过程中,电机转速设置2 400 r/min,轴承承受的径向力10 kN,采样频率25.6 kHz,采样间隔1 min,每次采样时长1.28 s。在轴承加速寿命试验结束后,轴承3_1表面出现了外圈故障,而轴承3_4存在内圈故障,如图4所示。因此,本文采用轴承3_1和轴承3_4的全寿命周期数据进行分析。
ABLT-1A轴承加速寿命试验数据源自东南大学机械工程学院的状态监测与故障诊断研究中心。图5所示的试验台主要由轴承测试模块、传动系统、加载系统、润滑系统、电气控制系统、计算机监控系统等部分组成。在实验过程中,轴承测试模块装有4个轴承,轴承型号为HRB6308,滚动体直径为15.081 mm,节圆直径为65.5 mm,滚动体数量为8个,接触角为0°。为了加速轴承的性能退化,在径向加载油缸内安装径向大活塞,采用径向大活塞对测试轴承进行径向加载。具体地,通过加载系统在设备运行过程中定期添加一定质量的砝码,使得每个轴承受到一个近15 kN的径向载荷。此外,测试过程中,电机转速平均稳定在3 000 r/min,采样频率设定为25.6 kHz,3个PCB加速度计以垂直方向安装在轴承座上对整个轴承全寿命数据进行测量,并通过NI9234数据采集卡和搭建的LabVIEW监测软件,每隔15 s采集并保存1组轴承振动加速度数据。当测试轴承在负载下连续运行10 h后,由于振动均方根超出了预定阈值,试验设备发生停机。通过线切割技术将 4个轴承切开,明显发现轴承 2的滚动体表面出现局部剥落故障,如图5所示。因此,本文采用轴承2的全寿命周期数据进行分析。
在实际中,轴承故障程度的识别要比轴承故障类型的识别更加困难。目前,对于轴承全寿命过程,没有明确的准则被用于确定和划分轴承性能退化阶段,即全寿命过程中轴承故障程度是不易辨识的。为解决这一问题,现有许多研究学者通过根据一些指标(如峭度、均方根、能量或信息熵)对轴承性能退化阶段进行大致划分,从而获取不同故障程度的轴承振动数据,并采用基于熵值理论的特征提取及诊断方法,实现不同轴承故障程度的识别。因此,基于前人研究,为了实现轴承故障模式及程度的有效识别,本文首先选用均方根指标对 2组试验的整个轴承性能退化数据进行划分,获取不同故障程度的轴承振动数据。然后,采用参数优化的HMDE提取轴承故障特征信息,并结合支持矩阵机进行轴承故障程度识别。
3.2 结果与分析
首先,采用均方根指标对 2组轴承加速寿命试验数据(XJTU-SY和ABLT-1A)进行划分,获取不同轴承状态数据。表4列出了不同轴承状态数据的详细信息,包括每种轴承状态的样本数及其对应的均方根。如表4所示,对于XJTU-SY轴承数据集,将轴承3_1全寿命数据中第525、2 350、2 475和2 538 min对应的4组数据作为 4种轴承状态(即正常、外圈轻微故障、外圈中度故障、外圈严重故障),同时将轴承3_4全寿命数据中第1 417、1 445和1 479 min对应的3组数据作为其他3种轴承状态(即内圈轻度故障、内圈中度故障和内圈严重故障),共7种轴承状态,每种轴承状态具有50个样本,每个样本包含2 048个数据点,随机选取每种轴承状态的25个样本作为训练,剩余样本作为测试,即训练集和测试集都包含7×25=175个样本。对于ABLT-1A轴承数据集,将轴承2全寿命数据中第85、280、291和292 min对应的4组数据作为4种轴承状态(即正常、滚动体轻微故障、滚动体中度故障、滚动体严重故障),每种轴承状态具有60个样本,随机选取每种轴承状态的30个样本作为训练,剩余样本作为测试,即训练集和测试集都包含4×30=120个样本。值得说明的是,在2组试验中,每种轴承状态的样本均是通过数据分割方法[25](即采用一个滑移窗)得到的。限于篇幅,图6仅绘制了不同的外圈轴承振动信号的时域波形和包络谱。图7为不同状态下滚动体振动信号的时域波形和包络谱。如图6和图7所示,随着轴承外圈故障或滚动体故障程度的加深,包络谱中轴承外圈故障特征频率fo=123.32 Hz或滚动体故障特征频率fb=102.8 Hz处的幅值越来越明显,这与实际轴承故障演化规律相符合。

表4 不同轴承状态数据Table 4 Data of different bearing conditions
然后,采用本文方法进行轴承故障特征提取和智能诊断。限于篇幅,图8仅显示了本文方法对XJTU-SY轴承数据集获得的混淆矩阵。在混淆矩阵中,横坐标序号1~7分别表示预测的7种轴承状态,纵坐标序号1~7分别表示实际的 7种轴承状态(即正常、外圈轻微故障、外圈中度故障、外圈严重故障、内圈轻度故障、内圈中度故障和内圈严重故障)。混淆矩阵中的对角线数值表示不同轴承状态对应的识别精度。从图8可以看出,6种轴承状态(即正常、外圈轻微故障、外圈中度故障、外圈严重故障、内圈轻度故障、内圈中度故障)的识别精度都是100%(即混淆矩阵对角线前6个数值均为1),而第 7类轴承状态(内圈严重故障)的一个样本被错误分为第 1类轴承状态(正常),其识别精度仅有 96%(24/25),相当于 0.96。因此,在测试集中,本文方法正确识别了174个数据样本,仅有1个数据样本被误分。也就是说,本文方法取得了99.43%(174/175)的识别精度,验证了本文方法在识别不同轴承状态中的有效性。
最后,为了突出本文方法的优势,将本文方法与 7种同类型诊断方法(即RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE)进行对比分析。为了避免诊断结果的偶然性,每种算法都进行5次试验。此外,为了确保算法对比的公平性,7种对比算法的重要参数均通过鸟群优化算法进行自适应选取,各参数优化结果如表5所示。值得注意的是,由于 RCMDE、GCMPE、GRCMSE、HFE和HSE算法对于每个样本提取的特征信息属于向量形式,因此,这 5种对比算法的分类过程都通过SVM来完成,且各分类模型参数均采用默认值(即惩罚参数C1=1,核参数λ=1/n),其中n为提取的故障特征维度。与提出方法一样,MHMDE和HMPE的分类过程均采用SMM来完成。表6列出了不同方法5次试验结果的平均识别精度准确率和标准差。从表6可看出,对于XJTU-SY轴承数据集,本文方法的平均识别精度为99.66%,标准差为 0.312。与 RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE相比,本文方法的标准差更小(即算法稳定性更好),平均识别精度分别提高了3.89、12.34、6.63、9.15、7.09、0.81和2.63个百分点。对于ABLT-1A轴承数据集,本文方法的平均识别精度为99.34%,标准差为0.371。与7种对比方法(即RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和HMPE)相比,本文方法的平均识别精度分别提高了2.17、3.51、6.17、9.51、11.51、1.17和 3.01个百分点。由此可知,相比传统的基于多尺度熵或层次熵的智能故障诊断方法,本文方法在识别滚动体故障程度方面具有一定优越性。需要说明的是,目前存在许多其他的先进分类模型,如非并行最小二乘支持矩阵机[26]、卷积神经网络[27]、自编码器[28]。因此,在将来的工作中,本文方法中的分类过程可以采用这些先进的分类模型替代 SMM 进行轴承故障类型识别。

表5 不同对比方法的参数设置Table 5 Parameter settings for different contrast methods
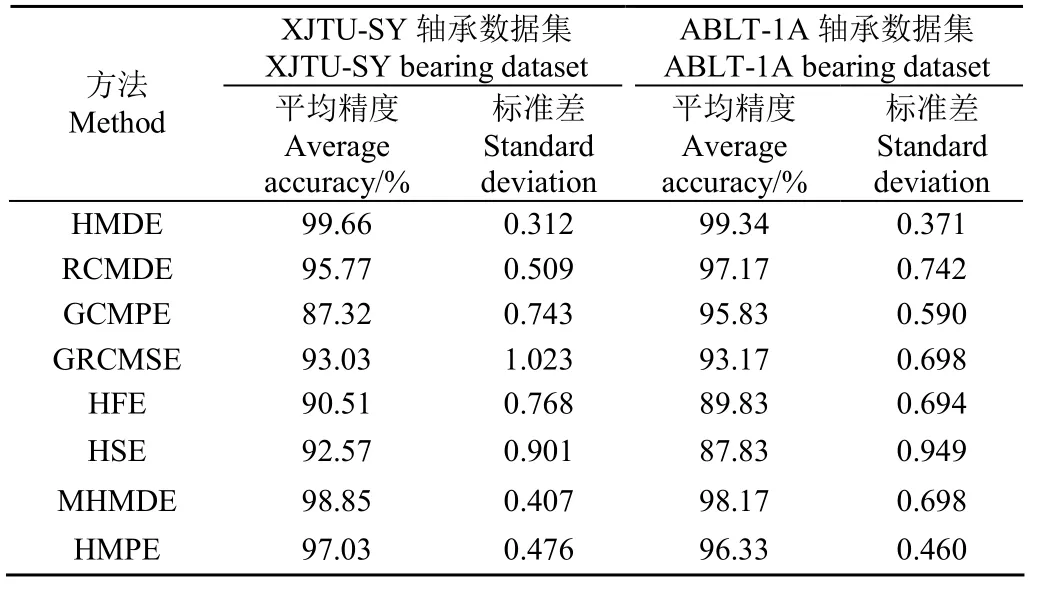
表6 不同诊断方法的对比结果Table 6 Comparison results of different diagnosis methods
4 结 论
1)针对全寿命周期内滚动轴承故障模式与程度难以有效识别的问题,提出了一种基于层次多尺度散布熵的滚动轴承智能诊断方法。该方法采用了BSA算法自适应优化HMDE的重要参数,避免了HMDE在特征提取过程中因人工选取参数而影响诊断效果的问题,同时兼顾了SMM在处理多维特征矩阵方面的优点。
2)通过试验分析对本文方法在轴承故障模式与故障程度识别中的有效性进行了验证。试验结果表明:对于第1和第2组试验,本文方法的平均识别精度可分别达到99.66%和99.34%。相比RCMDE、GCMPE、GRCMSE、HFE、HSE、MHMDE和 HMPE方法,本文方法在第 1组试验中的平均识别精度分别提高了3.89、12.34、6.63、9.15、7.09、0.81和2.63个百分点。本文方法在第2组试验中的平均识别精度分别提高了2.17、3.51、6.17、9.51、11.51、1.17和3.01个百分点。
