液压半挂运输车转向系统优化设计
2021-09-03田华良孙存良
田华良 孙存良 王 健
郑州新大方重工科技有限公司 郑州 450000
0 引言
由于我国经济发展和产业分布存在地域差异,长大超重货物的跨地域运输日益频繁,常规半挂车配置普通挂车桥和机械鹅颈,其车轮和鹅颈不具备转向能力,存在转弯半径大的问题,在半径较小的转弯过程中会出现严重的轮胎磨损现象。由于承载能力和转弯性能的不足,常规半挂车已无法满足长大超重货物的运输要求。
某液压半挂车由液压动力鹅颈和平板挂车组成,平板挂车共有10 个行走轮组,采用2 纵列5 轴线布局方式,其中前轮组为2 轴线,后轮组为3 轴线。在正常运输过程中,牵引车通过动力鹅颈与半挂车铰接。当牵引车牵引半挂车转向时,牵引车与半挂车会出现折腰运动,动力鹅颈将折腰运动传递给半挂车前行走轮组(后轮组不转向),稳定状态时牵引车转向瞬心与半挂车转向瞬心重合,形成共同转向中心O(见图1),不仅大大减小了转弯半径,而且还能保证多个轴线上的轮胎处于纯滚动状态,减小行驶阻力,并显著减少轮胎磨损量。
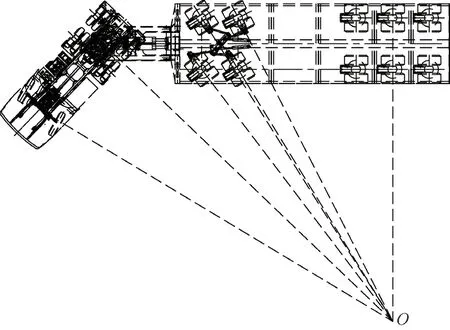
图1 牵引车与半挂车协同转向模式
1 转向系统构成及工作原理
液压轴线半挂车转向系统分为鹅颈转向机构和挂车转向机构两部分,鹅颈转向机构负责接收牵引车折腰运动,并把这种折腰转向运动传递给挂车转向机构,进而推动行走轮组转向。鹅颈转向机构由鹅颈转盘、转向摇臂、前转向液压缸等组成(见图2),挂车转向机构由中心转臂、转向拉杆、转向节臂、后转向液压缸、行走轮组等组成(见图3)。
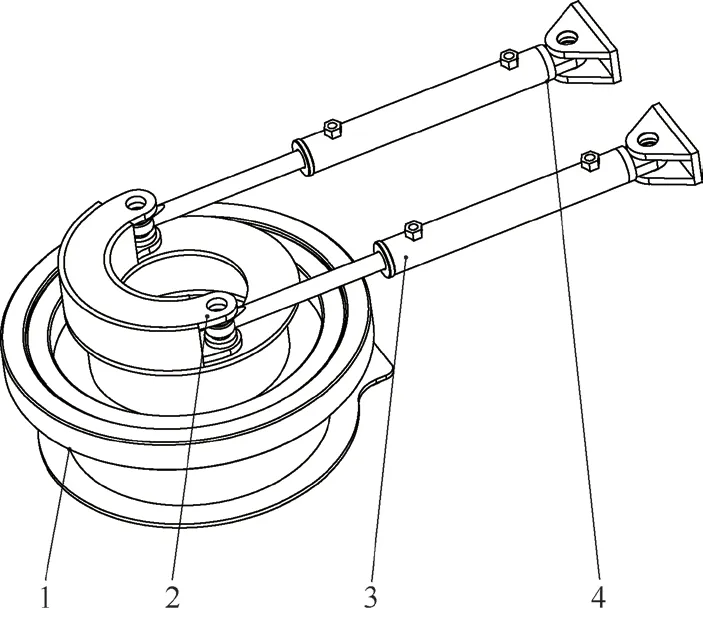
图2 鹅颈转向机构
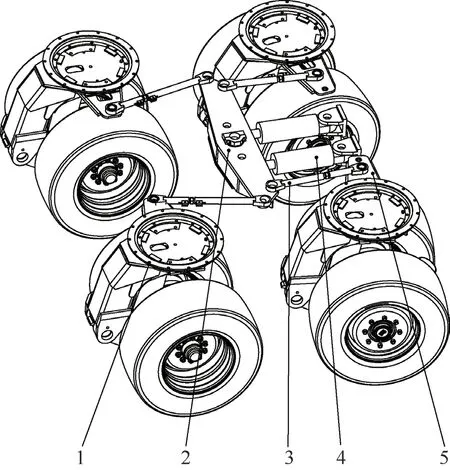
图3 挂车转向机构
由于鹅颈转向机构和挂车转向机构的距离较远,且鹅颈存在俯仰运动,如果采用常规的连杆机构传递转向运动,则需多级转换,受到结构的限制,这种方式制造装配复杂,自重较大。而液压传递转向方式不受结构限制,布管自由,安装便捷,自重和成本均较低,故通过柔性液压管连接的液压传递转向系统成为优选方案。
前转向液压缸与后转向液压缸由液压胶管连接,牵引车与半挂车的折腰运动推拉前转向液压缸,进而将液压油压进后转向液压缸,通过中心转臂带动转向拉杆和转向节臂驱动行走轮组转向。
2 转向系统
当牵引车牵引半挂车转向时,半挂车后轮组固定(不转向),前轮组跟随牵引车转向。牵引车鞍座中心基本与其2 根驱动轴的中间位置重合,协同转向时形成平面内2 个刚体的相对回转运动,牵引销位置是牵引车和半挂车的等速点,此点形成虚拟车轮,其转向角度与前轮组转角符合阿克曼原理。虚拟车轮的轴线与挂车前轮组各车桥轴线会交与回转中心O(见图4),O点处于后轮组中间轴线延长线上。
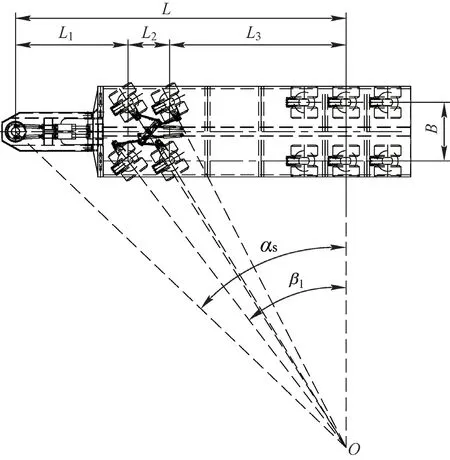
图4 半挂车转向状态示意图
在折腰转向过程中,鹅颈转向机构的左右液压缸做伸缩运动,前转向液压缸Lg 的无杆腔与前转向液压缸Rg 的有杆腔连接,后转向液压缸Lt 的无杆腔与后转向液压缸Rt 的有杆腔连接,二者由液压胶管连接。前转向液压缸Lg 的有杆腔与前转向液压缸Rg 的无杆腔连接,后转向液压缸Lt 的有杆腔与后转向液压缸Rt 的无杆腔连接,二者由液压胶管连接,并在管路上布置蓄能器。在两个回路上设置预充压接口,通过外置泵站可为两个回路预充一定压力[1],从而提高转向响应速度。经过简化的液压传递转向系统原理如图5 所示。
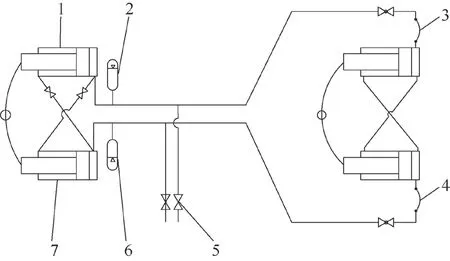
图5 液压原理图
牵引车与半挂车折腰转向运动是整车转向的驱动源,折腰转向角度为αs,第一轴线左侧行走轮组的转角为β1,第一轴线右侧行走轮组的转角为β1′,第二轴线左侧行走轮组的转角为β2,第二轴线右侧行走轮组的转角为β2′。
根据阿克曼原理可得
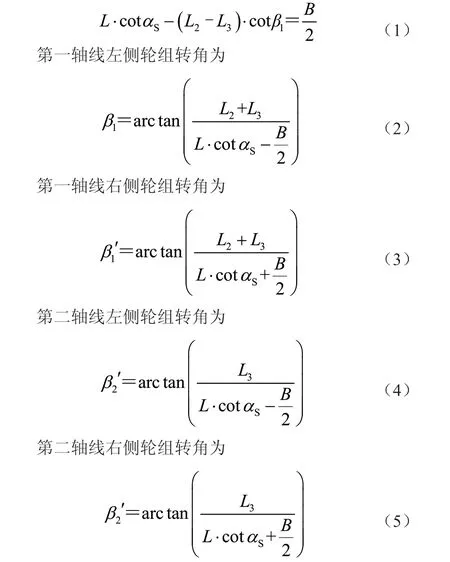
式中:B为跨距,B=2 250 mm;L1为第一基距,L1=4 365 mm;L2为轴距,L2=1 600 mm;L3为第二基距,L3=6 770 mm。
由于液压传递转向系统中配置有蓄能器、液压管路等,在转向过程中因地面阻力的影响,鹅颈转向角度达到一定角度后才能有足够的压力驱动挂车转向液压缸,进而推动行走轮组转向。因此,仅通过机械杆系优化无法得到刚柔耦合转向系统的最优解,应采用机液联合仿真的方法进行优化计算,避免繁琐的动力学方程及传递函数推导,为复杂机液系统设计提供有效手段。
2.1 转向系统多体动力学模型
利用多体动力学软件建立仿真模型(见图6),模型左侧为鹅颈转向机构,在中心摇臂上施加回转驱动Rsteering 来模拟折腰转向运动,中心摇臂的摆动带动前转向液压缸Lg 和Rg 做伸缩运动,建立前转向液压缸Lg 和Rg 的行程变化测量值SL_g和SR_g。右侧为挂车转向机构,在后转向液压缸Lt 和Rt 上分别施加驱动力SL_g和SR_g,后转向液压缸Lt 和Rt 推拉中心转臂,进而通过转向拉杆驱动行走轮组转向。
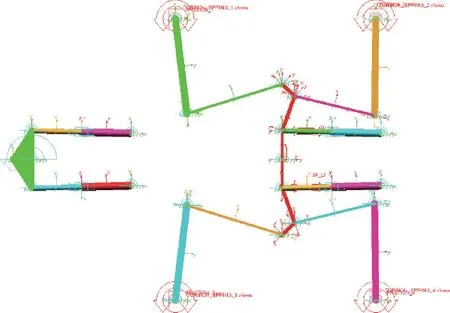
图6 转向系统多体动力学模型
单个行走轮组额定承载15 t,轮胎与地面滑动摩擦系数为0.8,根据轮组结构尺寸等可计算单个轮组的转向力矩为1.1×104N·m,并施加到行走轮组回转中心位置。
2.2 液压传递转向液压系统模型
在液压仿真软件中建立图7 所示液压仿真模型,液压传递转向是一个较复杂的机械液压综合系统,在液压模型中添加IB(Interface block)模块,可将机械模型中的鹅颈转向液压缸Lg 和Rg 的行程变化值SL_g和SR_g施与液压模型中前转向液压缸,将液压模型中挂车转向液压缸的作用力FL和FR回传给机械模型中驱动中心摇臂摆动,并将机械模型中右转向液压缸的行程变化值SL_Out和SR_Out施与液压模型的挂车转向液压缸,从而实现机械模型和液压模型的联合[2]。
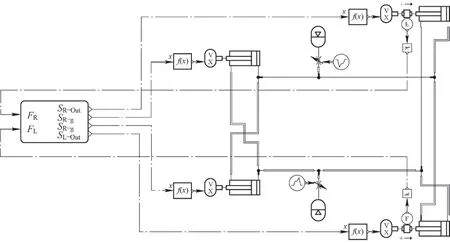
图7 转向系统液压系统仿真模型
建立液压仿真模型所需的结构参数有:前后转向液压缸的活塞直径为140 mm,活塞杆直径为70 mm,活塞行程为400 mm。油液运动黏度为5.1×10-5m2/s,弹性模量为1 700 MPa,油液温度为40℃。连接液压胶管直径为25 mm,长度按照各段实际尺寸设置。蓄能器初始容积为1.5 L,充气压力为1.1×107Pa,管路预充压1.3×107Pa。在转向过程中,蓄能器压缩和膨胀过程比较快,属于绝热过程,但蓄能器壳体与外界存在一定的热交换,故气体多变指数取1.3[3]。
3 联合仿真优化计算
当行走轮组转角误差在6°以内时,由于轮胎弹性变形,几乎感觉不到车轮的横向滑移。当转角误差超过7°时,车轮会产生明显的横向滑移,轮胎磨损加剧,同时地面产生明显痕迹,行驶性能也变得较差[4]。
液压挂车具备左右2 个方向的转向能力,为了保证左右2 个方向的转向性能一致,转向杆系按照左右对称设计,优化算法的目标是最小化左右轮组转向过程中的最大转角误差。
在转向系统多体动力学模型中,建立第一、二轴线4 个行走轮组的实际转向角度测量:第一轴线左侧车轮转角βt1、第一轴线右侧车轮转角βt1′、第二轴线左侧车轮转角βt2、第二轴线右侧车轮转角βt2′。
3.1 最小化的目标值
1)第一轴线左右2 个行走轮组的最大转角误差为

3.2 优化变量
第一轴线行走轮组转臂铰点的坐标X=DV_1、Y=DV_2;第一轴线转向摇臂铰点坐标X=DV_3、Y=DV_4;第二轴线行走轮组转臂铰点的坐标X=DV_5、Y=DV_6;第二轴线转向摇臂铰点坐标X=DV_7、Y=DV_8。
3.3 优化计算
采用OPTDES-GRG 优化算法进行优化计算,在优化过程中,多体动力模型与液压仿真模型实时进行数据传递。经过多轮优化计算,鹅颈转角范围为0°~45°,第一轴线左右2 个行走轮组的最大转角误差均小于1.5°。鹅颈转角范围为45°~50°时,第一轴线左右2 个行走轮组的最大转角误差逐渐增大;鹅颈转角为50°时,最大转角误差为4.74°(见图8)。
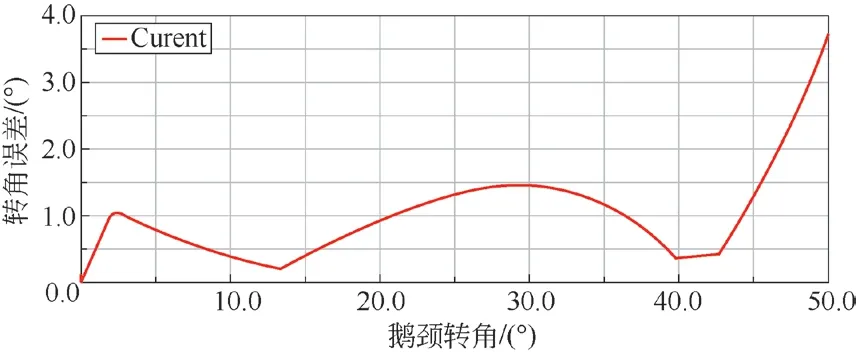
图8 第一轴线左右行走轮组的最大转角误差
当鹅颈转角范围为0°~42°时,第二轴线左右2 个行走轮组的最大转角误差均小于2.2°,鹅颈转角范围为42°~50°时,第二轴线左右2 个行走轮组的最大转角误差逐渐增大;当鹅颈转角为50°时,最大转角误差为4.82°(见图9)。

图9 第二轴线左右行走轮组的最大转角误差
4 结论
当鹅颈转角范围为0°~42°时,液压半挂车第一、二轴线左右轮组的转角误差均小于2.2°,第一、二轴线左右轮组的最大转角误差出现在鹅颈最大转角50°时。而在工程实际中,鹅颈达到50°的工况较少,即使达到50°,所经历的时间也很短,故可认为优化后的转向机构满足液压半挂车转向性能要求。
相比忽略液压回路影响的传统机械杆系优化方法,采用机液联合仿真优化,可以综合考虑转向阻力矩、液压蓄能器容积、蓄能器充气压力、液压缸尺寸、相应液压管路及油液特性等因素对转向系统的影响,为液压半挂车牵引转向系统的设计开发提供了有效方法。
