SBAS InSAR与GM(1,1)模型在青岛地铁13号线地表形变监测中的应用
2021-09-03郭在洁陶秋香王凤云韩宇
郭在洁 陶秋香 王凤云 韩宇
山东科技大学测绘与空间信息学院,山东青岛266590
地铁的建设和运营中,由于人为因素和自然因素的影响,地质条件发生变化,可能引发地铁沿线地表形变和坍塌[1-2],对沿线地面建筑物、构筑物、地下管线、各种设施、城市道路等造成不同程度的损害。因此,对地铁沿线的地表形变进行监测极为重要[3]。
随着空间对地观测技术的不断发展,合成孔径雷达干涉测量(Interferometric Synthetic Aperture Radar,InSAR)技术逐渐成为城市地面沉降、矿区地面沉降、山体滑坡等地表形变监测的重要技术手段[4]。贾煦等[5]利用欧空局37景ENVISAT ASAR数据,基于永久散射体合成孔径雷达干涉测量(Persistent Scatterers Interferometric Synthetic Aperture Radar,PS-InSAR)技术获取北京地铁15号线的地表形变情况。刘琦等[6]利用85景Sentinel-1A SAR影像数据和PS-InSAR技术获取了佛山市地铁沿线的地表形变情况。刘凯斯等[7]基于PS-InSAR技术和熵值法研究了北京地铁6号线沿线的地表形变分布情况。石晓宇等[8]利用合成孔径雷达差分干涉测量(Differential InSAR,D-InSAR)技术和灰色理论模型GM(1,1)(Grey Model,GM)对矿区沉降进行了监测与预测。刘哲[9]基于DInSAR技术和GM(1,1)模型对矿山地表形变进行监测与预测。
本文利用小基线集(Small BAseline Subset,SBAS)InSAR技术对37景Sentinel-1A SAR影像数据进行处理,获取了青岛地铁13号线积米崖站—世纪大道站沿线的地表形变信息,并对重点沉降区域进行分析;通过均匀提取地铁中心线上高相干点的地表形变值,计算地铁中心线的形变梯度,进而分析地铁沿线的稳定性;通过提取地表形变较严重的高相干点的时序累积形变信息,利用GM(1,1)模型对其地表形变过程进行数值摸拟和预测,研究GM(1,1)模型在地铁地表形变监测中的应用。
1 研究区概况和数据来源
1.1 研究区概况
青岛地铁13号线坐落于青岛市黄岛区,于2015年开建,2018年底正式开通运营。黄岛区位于北纬35°35′~36°08′,东经119°30′~120°11′,南临黄海,北靠胶州市,西邻诸城市、五莲县和日照市。年平均降水量696.9 mm,年平均气温12.7℃,空气湿度大,四季分明,具有明显的海洋气候特点。
1.2 数据来源
哨兵1号(Sentinel-1)卫星是全球环境与安全监测(Global Monitoring for Environment and Security,GMES)中的地球观测卫星,由两颗卫星组成,搭载有C波段的合成孔径雷达。首颗卫星于2014年4月发射,其重访周期为12 d。两颗卫星协同工作,重访周期缩短为6 d[6]。其中,干涉宽幅模式的幅宽为250 km,地面分辨率为5 m×20 m,数据可以从欧洲空间局网(https://scihub.copernicus.eu/dhus/)下载[7]。选取覆盖研究区的37景C波段、VV极化的Sentine-1A降轨数据,时间跨度为2018年1月16日至2020年8月9日。此外还用到了美国国家航空航天局(National Aeronautics and Space Administration,NASA)90 m的SRTM DEM高程数据消除地形相位引起的误差。
2 原理与方法
2.1 SBAS InSAR原理
假设某一个区域内有t0,t1,…,tN(t0,t1,…,tN为影像对应的时刻)共N+1幅单视复数(Single Look Complex,SLC)SAR影像,通过设置时间基线和空间基线阈值可以得到M幅差分干涉图,其中M的取值范围[10]为(N+1)/2≤M≤N( )
N+1/2。利用时刻tA和tB获取的2景影像生成第i幅差分干涉图(i=1,2,…,M,且时刻tA早于时刻tB),那么生成的差分干涉图上像元(x,r)(x为方位向坐标,r为距离向坐标)的解缠后的差分干涉相位Δφi(x,r)可表示为[10]
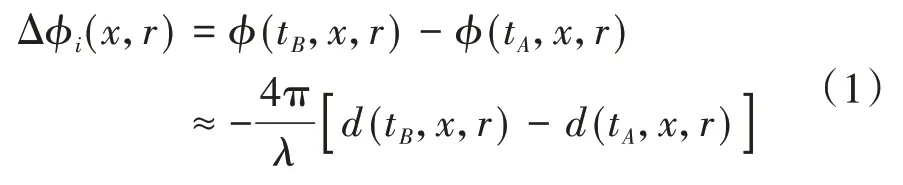
式中:φ(tA,x,r)和φ(tB,x,r)分别为像元(x,r)在时刻tA与tB相对于参考时刻t0的雷达视线向的累积形变相位;λ为雷达的波长;d(tA,x,r)和d(tB,x,r)分别为时刻tA与tB相对于参考时刻t0的雷达视线向的累积形变量。
对于参考时刻t0,有d(t0,x,r)≡0[10]。
若 令φ=[φ(t1,x,r),φ(t2,x,r),…,φ(tN,x,r)]T,Δφ=[Δφ1,Δφ2,…,ΔφM]T,则主影像和辅影像的时间序列TIEi、TISi分别为
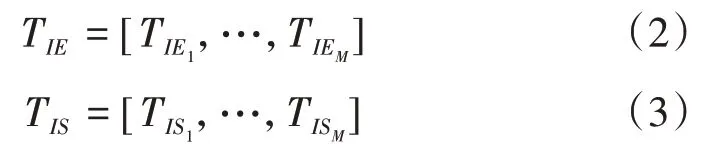
如果TIEi>TISi,则任意的差分干涉对对应的相位值为

式中:φ(TIEi)为主影像的相位值,φ(TISi)为辅影像的相位值。
对任一像元,可以列出一个SBAS InSAR的线性形变模型[10]

式中:A是一个M×N的矩阵,矩阵行对应差分干涉图,列对应SAR影像。
当所选数据均属于一个基线集,即基线集数量L=1时,A为N阶矩阵。若M=N,则方程只有唯一解;若M>N,则方程的解不唯一。矩阵可以利用最小二乘法解得φ的估计值[10],即
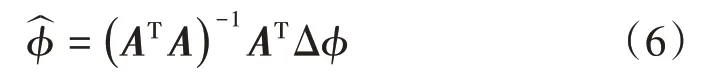
通常情况下,SAR影像的数据集分散在几个子集中。当L>1时ATA为奇异矩阵,矩阵A的秩为N-L+1,方程的解不唯一。为了得到唯一解,SBAS InSAR采用奇异值分解(Singular Value Decomposition,SVD)方法,将多个基线集联合,求出最小范数意义上的最小二乘解,得到累积形变量[10]。
2.2 GM(1,1)模型
邓聚龙教授在20世纪80年代提出了灰色系统理论,并用该理论解决信息不完备系统的复杂问题,根据已知数据建立模型来预测未来数据的发展趋势[11]。GM(1,1)模型是灰色1阶、1个变量的模型,具体建模过程如下。

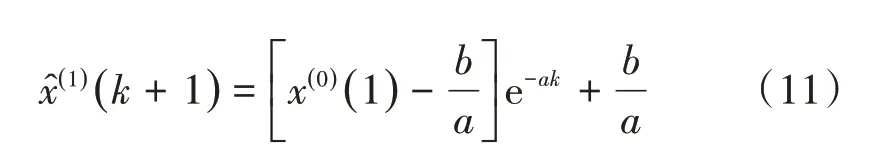
式(11)为数列的预测公式,是对一次累加生成数列的预测值[11-12]。
利用GM(1,1)模型对SBAS InSAR监测的地表形变量进行数值摸拟和形变预测,具体步骤如下:
1)提取感兴趣高相干像元(特征点)各成像时刻的累积形变量;
2)利用GM(1,1)模型对提取的特征点的前m个成像时刻的地表形变量进行数值摸拟,预测后(N+1-m)个成像时刻的形变量和后续SBAS InSAR未监测到的时刻的地表形变量;
3)对比分析SBAS InSAR地表形变监测结果和GM(1,1)模型模拟与预测的地表形变结果,对GM(1,1)模型进行精度验证,为地铁沿线后期沉降提供参考。
数据处理的具体流程见图1。
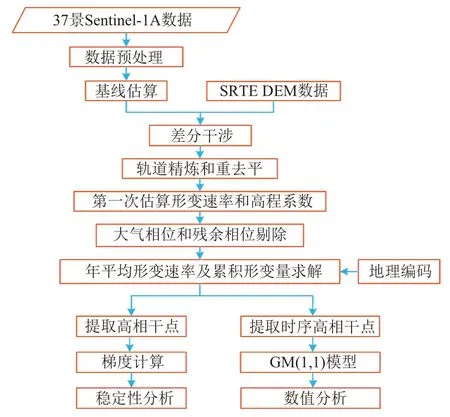
图1 数据处理流程
3 监测结果分析
3.1 地铁沿线地表形变
青岛地铁13号线于2017年10月实现洞通,2018年2月实现轨通,2018年12月26日正式开通运营。利用图1所示的数据处理流程和方法,对青岛地铁13号线积米崖站—世纪大道站37景Sentine-1A SAR数据进行处理,获取2018年1月16日至2020年8月9日地铁沿线的地表形变信息。对地铁沿线600 m缓冲区内的地表形变进行分析得到地铁沿线形变速率,见图2。可知:监测期内地铁沿线存在不同程度的地表形变,大部分区域的形变速率集中在-5~5 mm/a,形变比较明显的区域为学院路站、辛屯站、两河站、凤凰山路站附近,最大沉降速率分别为-10、-18、-9、-10 mm/a。
从形变明显的四个区域分别选取地表形变严重的点P1、P2、P3、P4(参见图2),其地表形变过程见图3。分别从建设期(运营前)和运营期进行分析。
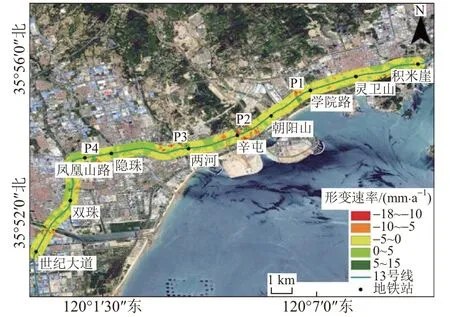
图2 地铁沿线600 m缓冲区内的形变速率
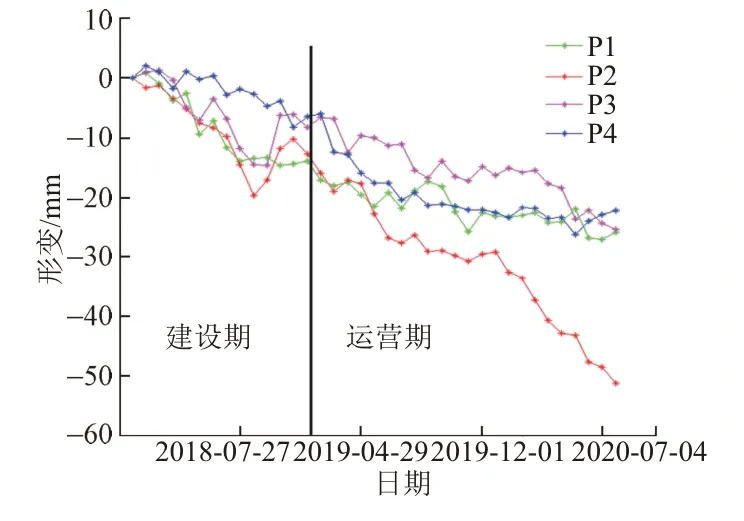
图3 4个特征点的时序形变结果
由图3可知:①对于P1点,在建设期一直处于快速波动下沉状态,在2018年月7月27日后趋于稳定,沉降值为-16 mm;地铁运营后开始“沉降→抬升→……→沉降”的波动式缓慢沉降。②对于P2点,在建设期沉降值在2018年8月20日出现了较大的波动;在地铁即将运营时,沉降值为-13 mm;地铁运营后一直处于波动式下沉状态;2019年8月27日后,沉降趋于稳定;2019年12月25日后沉降值直线式增大,其快速下沉的原因须实地勘察了解。③对于P3点,在建设期沉降值出现较大幅度的波动;地铁即将运营时,沉降值仅为-8 mm;地铁运营后呈现出波动式下沉,但是波动幅度并不大。④对于P4点,在建设期处于波动式下沉,但是整体波动幅度较小;地铁即将运营时,沉降值仅为-7 mm;运营后至2019年7月10日,该处的沉降处于直线式增大状态;之后沉降趋于稳定。⑤至2020年8月9日,P1、P2、P3、P4点的累积沉降量分别为-25、-51、-22、-25 mm。
3.2 地铁沿线地表稳定性
地表形变梯度描述地铁沿线一定区间内形变速率或形变量变化快慢的过程,主要用来反映形变在空间上的均匀性[4]。不均匀地表形变所带来的危害远高于均匀地表形变。分析地铁沿线的地表形变梯度对于地铁线路的建设和后期的稳定运营具有重要意义。
以积米崖站为起点,世纪大道站为终点,分别提取地铁中心线在2018年2月9日、2018年12月18日、2020年8月9日的累积形变量,见图4。
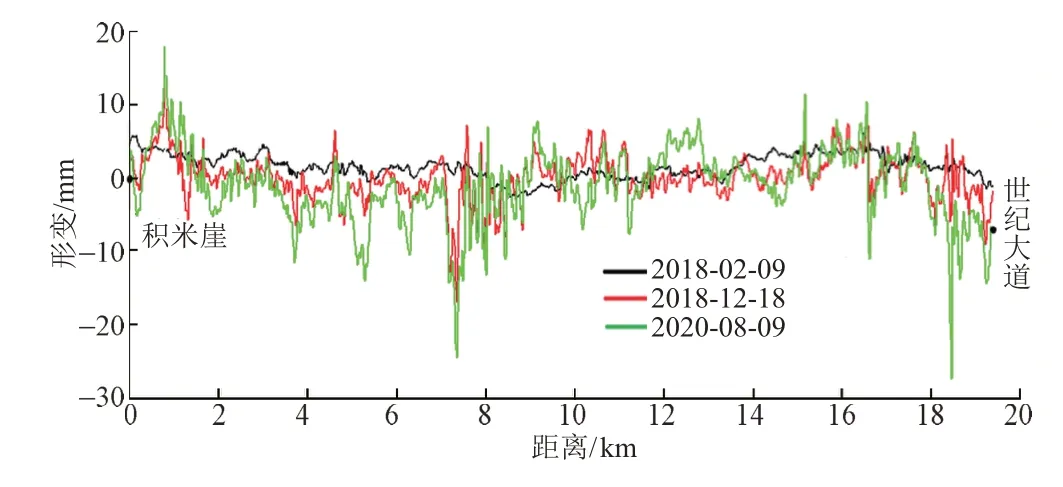
图4 地铁中心线地表累积形变量
从图4知:①在监测初期,地铁沿线地表处于稳定状态,地表形变非常小,几乎无沉降发生。②相比监测初期,在地铁即将开通时期(2018年12月18日),地表形变量和波动幅度都发生了较大变化,在距离起点7.0~7.8 km内,地表由抬升变为下沉,形变由2 mm减小到-18 mm。③在监测末期(2020年8月9日),地铁沿线的地表形变波动趋势基本和地铁即将开通时期的趋势一致,但地表形变量增大,在距离起点5.0~5.8 km处,沉降量由4 mm增加到14 mm;在18.5 km处,沉降量由5 mm增加到28 mm,变化幅度较大。
为了分析地铁沿线地表形变的稳定性,沿着地铁中心线的走向,提取高相干像元2020年8月9日的地表形变值,计算两个高相干像元间的形变梯度。计算公式为
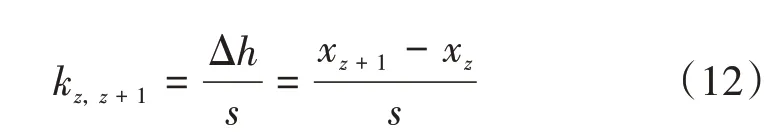
式中:kz,z+1为第z和第z+1像元间的地表形变梯度;xz为第z像元的地表形变值;xz+1为第z+1像元的地表形变值;s为第z和第z+1像元间的距离。
根据GB 50157—2013《地铁设计规范》,正线的最大坡度不宜大于0.3,困难地段不高于0.35。算得的地铁中心线地表形变梯度见图5。可知,地铁沿线地表形变梯度整体处于稳定状态,形变梯度大于0.3的位置主要在距离起点1.0、7.0~9.0、16.4、15.5、18.5 km处。其中,18.5 km处的地表形变梯度达到最大值1.3,在日常地铁运营和维护中,须重点监控该路段。
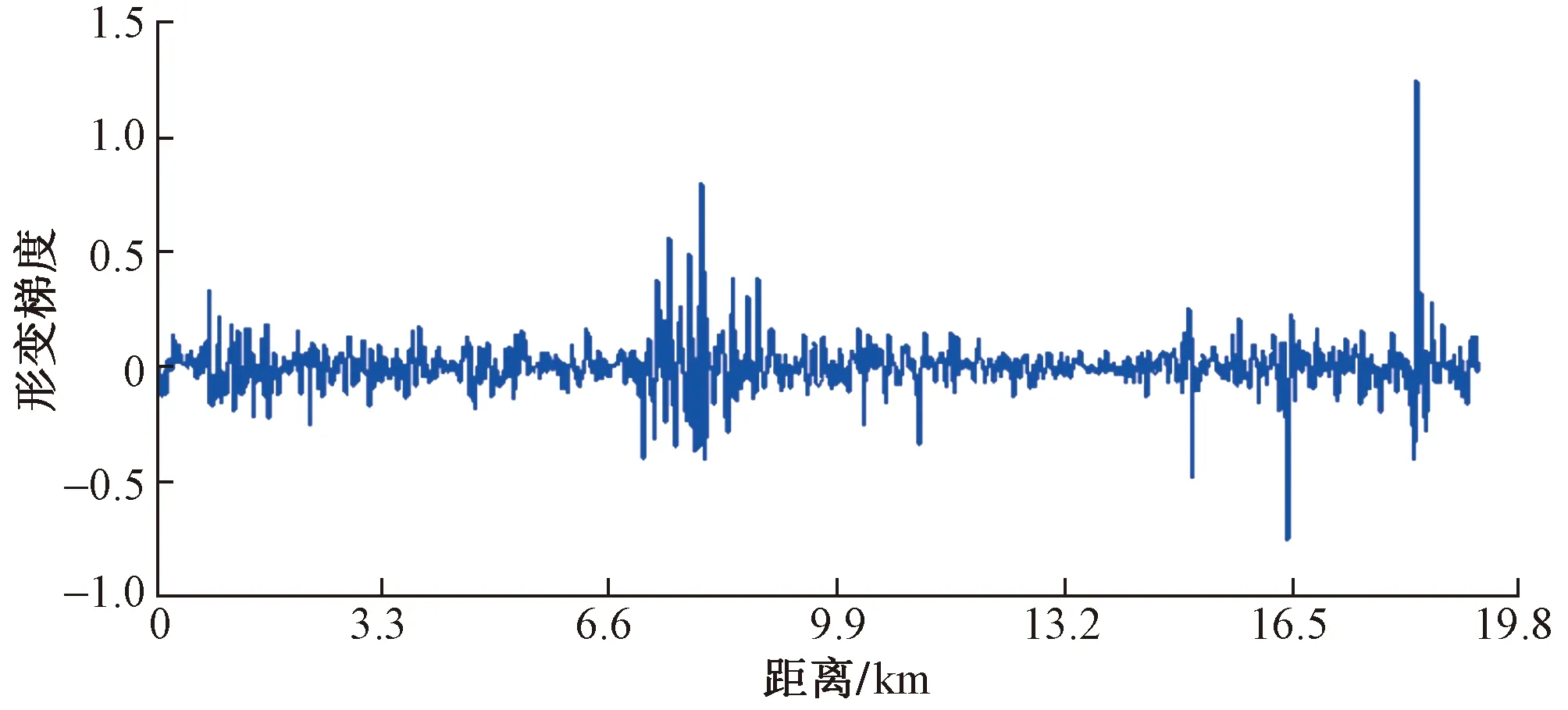
图5 地铁中心线地表形变梯度
以地表形变梯度分析地铁沿线地表形变的均匀性可以作为地铁建设和运营的重要参考依据,同时须要在运营过程中加强监测确认。
3.3 GM(1,1)模型在地表形变监测中的应用
以地表形变较严重的P1、P2、P3、P4点为例,利用GM(1,1)模型对4个点SBAS InSAR监测的前31期、34期、37期地表形变数据进行模拟,对后6期、后3期以及未来3期的地表形变进行预测,结果见图6—图9。可知:①根据GM(1,1)模型对P1、P2、P3、P4点SBAS InSAR监测的地表形变数据进行模拟与预测的结果,得到P1、P2、P3、P4点在2018年1月16日至2020年8月9日地表一直在缓慢沉降,其沉降趋势相似,都是以指数函数曲线的趋势缓慢沉降,无法真实反映“沉降→抬升→……→沉降”的地表形变过程。②GM(1,1)模型模拟与预测的P2、P3点地表形变曲线要比P1、P4点地表形变曲线精度要高,也更符合实际情况。这是因为P2、P3点在37景SAR影像监测期间总体呈现出波动式下沉的趋势;P1点在最后3个成像时刻,地表趋于稳定,甚至略有抬升;P4点在后15个成像时刻,地表趋于稳定,在最后4个成像时刻,地表逐渐抬升。③比较GM(1,1)模型模拟与预测的P2、P3点地表形变曲线发现,地表形变过程波动越小,形变数据的波动越小,GM(1,1)模型的模拟与预测精度就越高。图6—图9中第1个成像时刻和第2成像时刻的坡度较大也是由于地表形变过程的波动造成的。
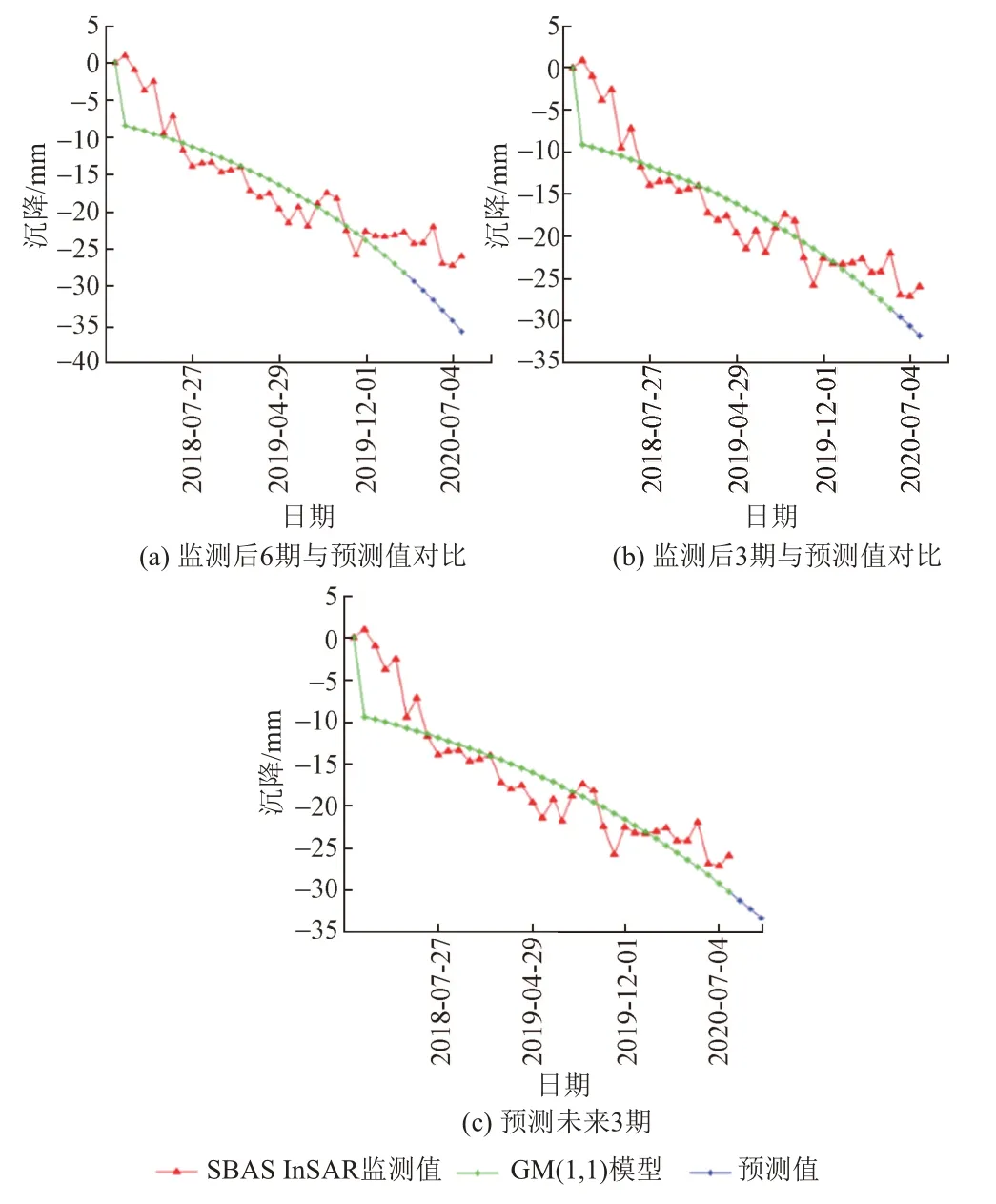
图6 GM(1,1)模型模拟与预测的P1点地表形变曲线

图7 GM(1,1)模型模拟与预测的P2点地表形变曲线

图8 GM(1,1)模型模拟与预测的P3点地表形变曲线

图9 GM(1,1)模型模拟与预测的P4点地表形变曲线
可见,GM(1,1)模型更适合对地表持续沉降或持续抬升且形变过程波动较小的特征点进行模拟和预测。
4 结论
1)利用SBAS InSAR技术能够监测和分析地铁沿线、周边区域及主要特征点大范围、长时间序列的地表形变时空分布,直观形象地展示其地表形变过程。
2)通过地铁中心线形变梯度分析,可以找出形变梯度偏大的区域。在日常地铁运营和维护中,须要重点监控这些路段。
3)GM(1,1)模型模拟和预测的地表形变曲线呈现出指数函数曲线的持续沉降趋势,更适合对地表持续沉降或持续抬升且形变过程波动较小的特征点进行模拟和预测。
本文研究成果将有助于推进InSAR技术和GM(1,1)模型在城市道路和地铁沿线地表形变监测中的应用。
