公路下穿铁路新建泡沫轻质土过渡段框架涵动力特性分析

姚洪锡 杨晨 黄俊杰 辛玺 刘彬彬

1.中铁第四勘察设计院集团有限公司，武汉430063；2.西南交通大学土木工程学院，成都610031；3.中国铁路武汉局集团有限公司，武汉430071；4.中铁武汉勘察设计研究院有限公司，武汉430074

泡沫轻质土是先由水泥、水、原料土（砂、砂性土或低液限土）按一定比例充分混合形成浆体，再与一定比例足够细小的稳定气泡群充分混合搅拌形成流体，并最终凝固成型的一种轻型填筑材料［1］。

文献［2-6］介绍了泡沫轻质土的基本概念及工程应用，在轨道交通领域，泡沫轻质土已经广泛应用于公路路基工程建设。文献［7-12］介绍了泡沫轻质土应用于公路路基工程中的一些案例，如公路桥涵台背填土、隧道脱空处理、公路路桥过渡段施工以及软土地基处理等。铁路领域应用泡沫轻质土的工程实例较少，文献［13-20］介绍了一些针对铁路工程应用泡沫轻质土的相关研究，泡沫轻质土应用于铁路路基施工中具有良好的施工性、环保性等优点，且能缩短施工工期，有效降低沉降，更好地控制新旧路基沉降不均匀造成纵向裂缝问题。目前，公路领域通用的泡沫轻质土湿密度主要在500～600 kg/m3，约为普通路基填料的1/3，将其引入铁路领域填筑路桥过渡段能减小过渡段自重，降低地基附加应力，控制过渡段工后沉降。此外，由于泡沫轻质土自重轻，可优化地基处理强度，降低地基处理费用。

将泡沫轻质土用于铁路领域填筑过渡段尚缺少工程实例且相关研究不多。因此针对武汉市李纸路下穿南环铁路上行线及京南（京广铁路—南环铁路）联络线框架桥涵两侧泡沫轻质土过渡段结构形式，建立车-轨-路涵过渡段三维有限元模型，分析在运营车辆作用下泡沫轻质土过渡段振动加速度、动应力、动位移沿纵向和竖向的变化规律，并将其与传统过渡段结构振动响应特性进行对比分析，为新建泡沫轻质土路涵过渡段设计提供理论依据。

1 工程概况

新建李纸路以框架桥方式下穿南环铁路上行线及京南联络线，该工程建设的关键技术难题是确保既有铁路线路运营安全。为此，提出的方案是首先采用纵横抬梁法架空铁路线路，然后开挖框架桥所需空间的土方（既有铁路路基基床和本体），再现浇框架桥，待框架桥混凝土养护完成后填筑框架桥台尾两侧过渡段和上部基床，接着拆除纵横抬梁，最后填筑道床、恢复线路运营。

台尾两侧新建的过渡段一般采用级配碎石填筑并对其进行注浆加固，根据类似工程实践经验，采用该方法新建的过渡段在恢复线路运营后往往会产生过大的差异沉降，后期需要开展多次垫道砟作业，才能保证线路的平顺性。施工范围内民房较多，征地困难，施工作业面小。因此，设计提出采用泡沫轻质土填筑台尾两侧过渡段。该工程纵断面设计如图1所示。

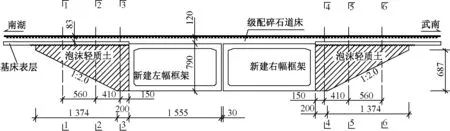
图1 工程纵断面设计（单位：cm）

框架桥主体采用2×15.55 m两孔框架地道桥形式，两侧既有路堤开挖成倒梯形过渡段，梯形上边长14.24 m，斜边坡率为1∶2。开挖边坡坡率为1∶2。台尾两侧过渡段基床底层及以下采用泡沫轻质土回填，基床表层0.6 m范围内采用掺5%水泥的级配碎石回填，道砟层厚0.5 m。

2 计算模型的建立

2.1 模型简介

根据工程情况建立了过渡段三维计算模型，如图2所示。车体采用整车模型，列车参数参考22型客车，车体长23.6 m，宽3.105 m，高4.28 m，自重45 t。考虑到动力计算增量步对模型计算精度的影响，对列车参数进行了适当优化。模型列车相关参数：车体质量为48 000 kg；转向架质量为3 200 kg；轮对质量为2 400 kg；车辆定距为17.375 m；转向架轴距为2.5 m；车体质心至轨面的高度为1.7 m；轮对质心至轨面的高度为0.46 m；转向架质心至轨面的高度为0.6 m；一系弹簧垂向刚度为1.87×106N/m；一系弹簧垂向阻尼为5×105N·s/m；二系弹簧垂向刚度为1.72×105N/m；二系弹簧垂向阻尼为1.95×105N·s/m。

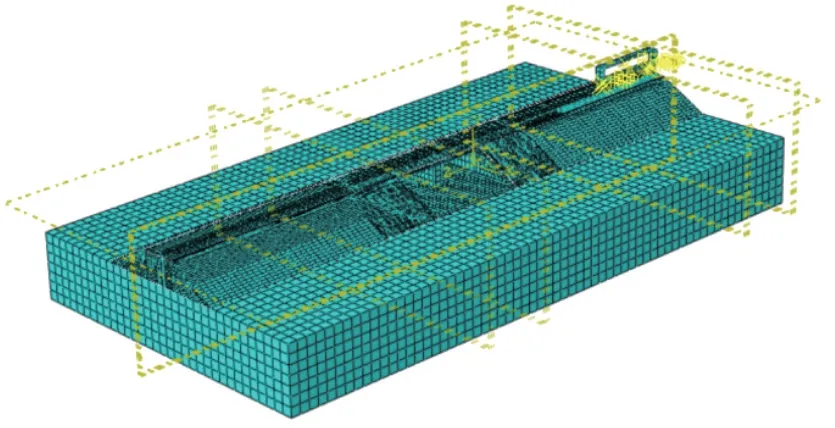
图2 三维过渡段模型

2.2 材料本构关系及相关参数

在有限元软件中给出了多种定义阻尼的方式，本文选择Rayleigh阻尼模型定义材料的阻尼。阻尼矩阵C是由质量矩阵M和刚度矩阵K按式（1）进行线性组合而成，计算式为

式中：α、β分别为质量阻尼系数、刚度阻尼系数，两者由选取的两阶参考频率及其对应的阻尼比决定。

在实际振动分析中，与两阶参考频率对应的阻尼比通常不会有很大变化，基本上为结构阻尼比ζ，则

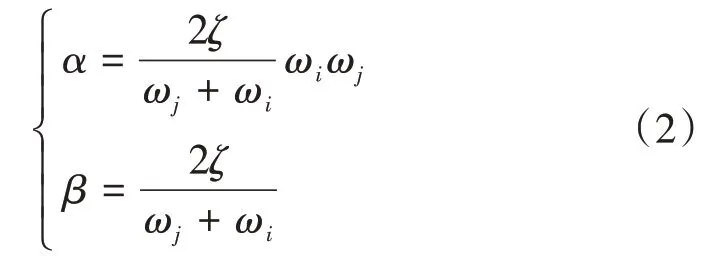
式中：ζ为结构阻尼比，由材料类型决定；ωi、ωj分别为第i阶、第j阶参考频率。

通常情况下，ωi为所关注部位的一阶自振频率。对模型进行模态分析，发现对动力反应有显著影响的高频振型而言，取前20阶频率即可。将模型进行模态分析后得到前20阶自振频率，见表1，模型参数见表2。

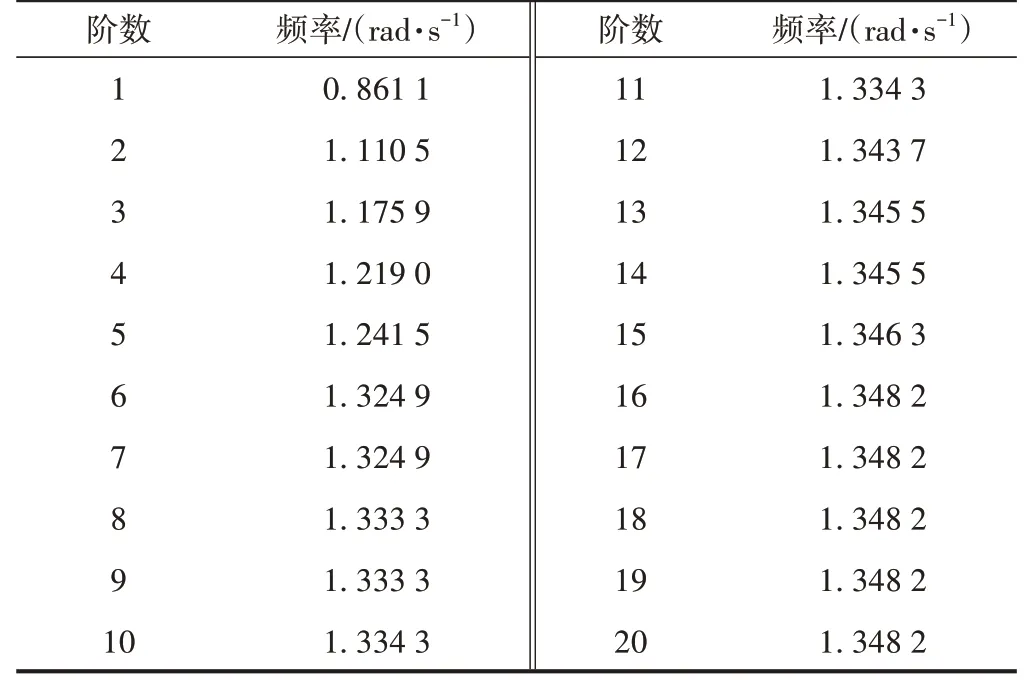
表1 模型前20阶自振频率

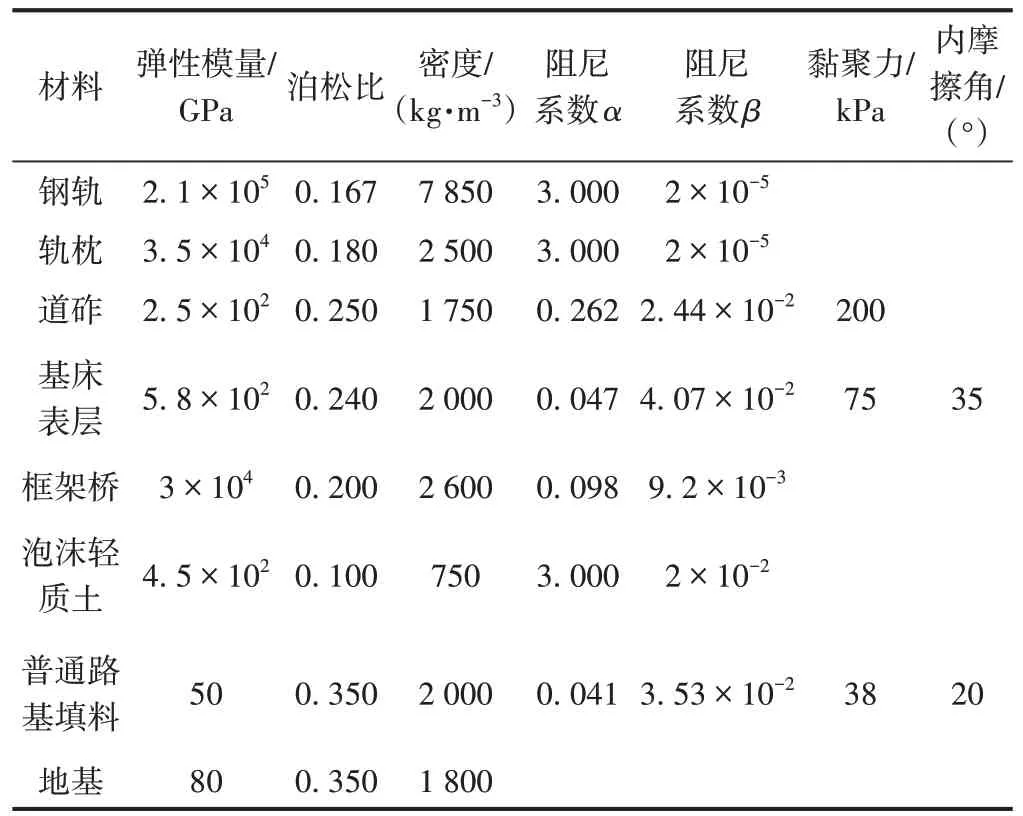
表2 模型参数

2.3 边界条件

根据模型的对称性，在模型的底部约束三个方向的平动与转动自由度，模型的左右及前后各约束相应方向的平动自由度。

对于车辆一系、二系悬挂系统，将其视为以一定速度运行于轨道结构上的多刚体系统，采用弹簧阻尼约束。转向架与轮对之间由一系弹簧和阻尼元件相连，构成一系悬挂装置；车体与转向架之间由二系弹簧和阻尼元件相连，构成二系悬挂装置［21］。

在有限元建模过程中，钢轨被简化为弹性点支撑的有限长梁模型，每一枕跨为一个梁单元，扣件被简化为弹簧阻尼连接件，轨枕简化为一个刚性的质量块，将轨枕结构与道砟层表面切削后形成整体部件。

2.4 荷载条件

荷载主要为运动车体重量，车体、转向架、轮对重量以集中荷载形式作用在对应部件重心处。依据铁路局提供的轨道不平顺数据，设置模型轨道平顺度，列车时速为120 km。

3 计算结果分析

在距台尾1.5 m（断面3-3和断面4-4）、5.6 m（断面2-2和断面5-5）和11.2 m（断面1-1和断面6-6）位置处创建拆分面，各断面位置参见图1。计算中按照模拟列车的行驶方向，依序通过断面1-1、2-2、3-3、4-4、5-5、6-6，即断面1-1、2-2和3-3为列车上桥侧，断面4-4、5-5和6-6为列车下桥侧。本文主要分析行车速度120 km/h的22型客车通过时泡沫轻质土过渡段加速度、动应力和动位移的分布规律。

3.1 加速度

不同断面在轮对中心位置处竖向加速度沿深度方向的衰减规律见图3。可知：竖向加速度随着竖向深度的增加而呈逐渐减小趋势，且在基床表层范围内衰减速度最快。过渡段范围内断面1-1、2-2、3-3、4-4、5-5、6-6处路基面加速度分别为1.302、1.795、2.145、2.066、1.851、1.157 m/s2，经过0.6 m厚级配碎石层后竖向加速度分别衰减11.40%、14.10%、14.70%、14.01%、18.40%、22.30%，到达基床底层底部位置时，加速度均小于0.6 m/s2。

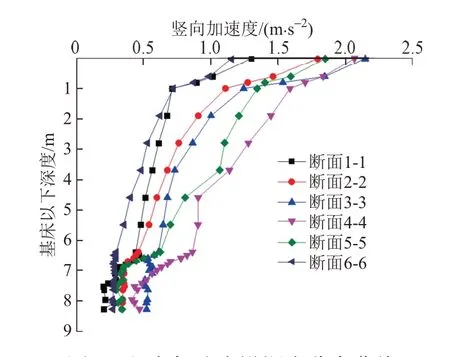
图3 竖向加速度沿深度分布曲线

文献［22］运用FLAC软件分别对采用加筋土和级配碎石填筑过渡段进行了动力响应分析。虽然其研究车速最低为160 km/h，而本模型计算行车速度为120 km/h，但其数据趋势仍然具有参考价值，振动加速度沿深度方向衰减情况与本模型计算结果对比见表3。本模型路基本体顶面加速度相对于基床表层顶面处衰减率为75.61%～84.3%，文献［22］中衰减率为85%（级配碎石）和90%（加筋土），本文计算结果与文献［22］结果较为接近。这说明采用泡沫轻质土填筑过渡段路基与采用级配碎石和加筋土填筑过渡段路基的处理效果相当。

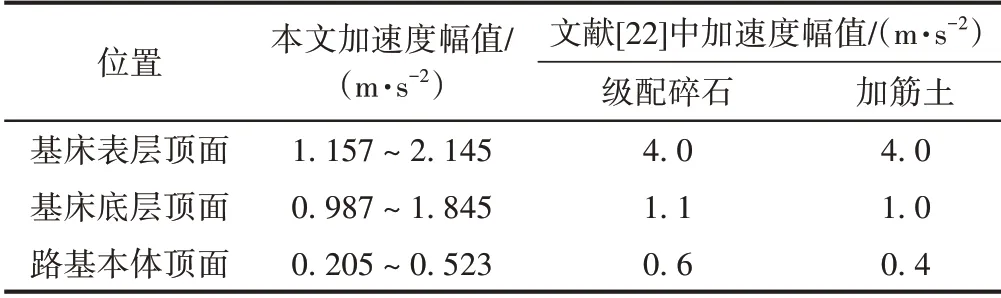
表3 加速度沿深度方向分布情况对比

3.2 动应力

列车通过时不同断面处动应力响应规律见图4。

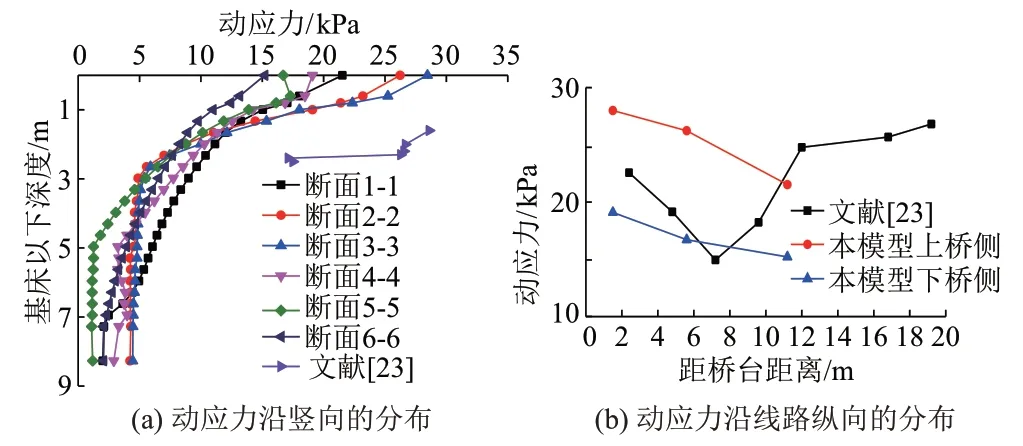
图4 动应力幅值沿竖向及纵向分布规律

由图4可知，竖向动应力随着竖向深度的增加而呈减小趋势，处于基床表层范围衰减速度最快。且由普通路基段向桥梁方向过渡时（即上桥侧）基床表层动应力较由桥梁向普通路基段过渡时（即下桥侧）大。过渡段范围内1-1、2-2、3-3、4-4、5-5、6-6断面处路基面动 应力 分别 为21.52、26.23、28.45、19.09、16.77、15.2 kPa，经过0.6 m厚级配碎石层后动应力分别衰减16.26%、11.56%、11.32%、13.49%、3.24%、11.68%，再经过泡沫轻质土层进一步动应力扩散和消能作用，路基面以下5 m深度之后各断面动应力相对于路基面均衰减超过2/3。文献［23］中通过对秦沈客运专线某路桥过渡段现场实测，得到过渡段路基动应力沿深度及纵向分布规律，该过渡段路基基床表层下方采用级配碎石填筑，路基横断面两侧采用A、B组粗粒土填筑。通过本模型计算结果与文献［23］现场实测结果对比发现，动应力沿深度方向衰减规律大致相同，沿线路纵向路基面动应力大小相近。由本模型计算结果发现路基面动应力呈上桥侧顺行车方向逐渐增大，以及下桥侧顺行车方向逐渐减小的规律。

3.3 动位移

基床表面在轮对中心位置处竖向动位移沿线路纵向的分布规律见图5。可知，由于框架涵为两孔框架地道桥形式，框架涵范围内桥面竖向动位移呈现出双峰分布规律，即桥柱顶面动位移较小，而两孔框架范围内动位移较大。两孔框架范围内位移最大值为1.14 mm，而桥柱范围内动位移为0.637～0.674 mm。两侧桥台处动位移分别为0.556 mm（上桥侧）和0.577 mm（下桥侧）。

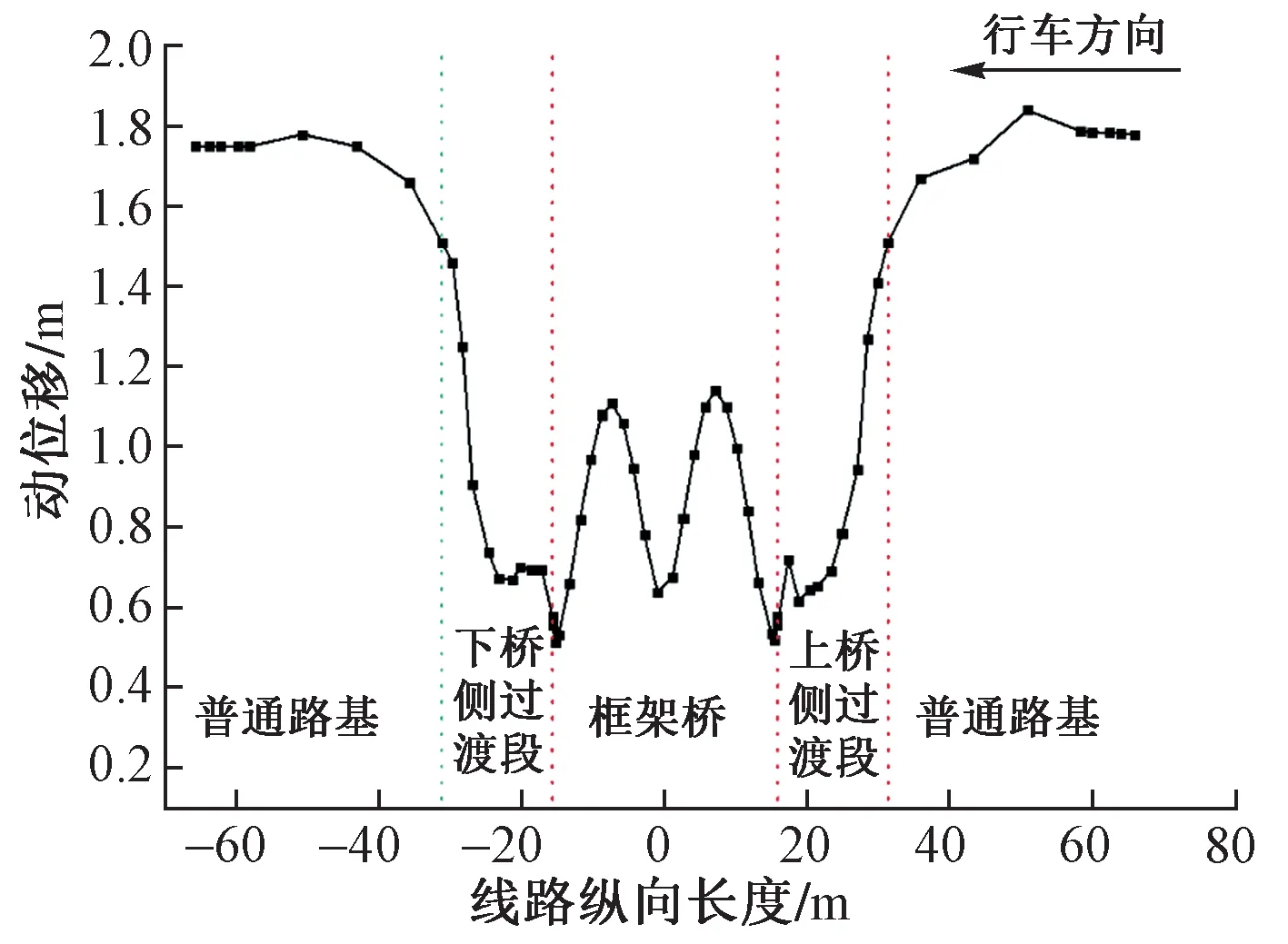
图5 竖向动位移幅值沿线路纵向的分布

列车上下桥两侧过渡段基床表层顶面（路基面）动位移沿线路纵向分布及大小无明显差距。动位移沿线路纵向靠近桥台大体呈现出递减趋势，过渡段距离桥台8～13 m内（即过渡段末端）动位移沿纵向递减速率明显较过渡段中部范围大。断面3-3动位移出现极大值0.72 mm，相较于上桥侧桥台，动位移高出0.164 mm。上桥侧靠近过渡段末端的断面1-1处路基面动位移为1.27 mm，相较于断面3-3增大了76.4%；下桥侧靠近过渡段末端的断面6-6处路基面动位移为1.25 mm，相较于靠近桥台的断面4-4增大了80.1%。

参考文献［24］中针对秦沈客运专线某过渡段基床表层面上（路基面）动位移响应进行了分析。其过渡段工点1路基部分采用倒梯形过渡，桥台与路基过渡段的基床表层采用土工格栅加固填筑，路基基床底层填筑级配碎石，路基横断面两侧填筑A、B组粗粒土，其间分层铺设土工格栅；工点2和3路基部分采用倒梯形过渡，桥台与路基过渡段的基床表层采用级配碎石填筑，路基基床底层填筑级配碎石，路基横断面两侧填筑A、B组粗粒土。本模型及文献［24］计算的路基面动位移见表4。文献［24］3个工点动位移最大值分别为1.624、0.337、1.334 mm，说明过渡段基床底层采用级配碎石填筑与采用泡沫轻质土填筑对路基面动位移最大值影响差异不大，由此可以说明过渡段范围内基床底层采用倒梯形填筑泡沫轻质土填料能够实现路桥平稳过渡。

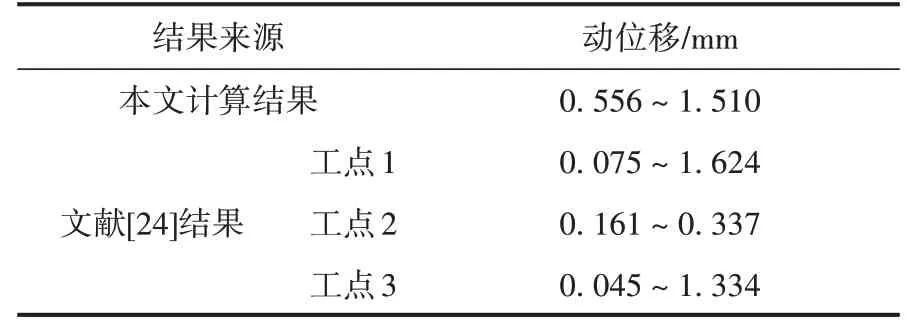
表4 过渡段范围内路基面动位移对比

4 结论

1）泡沫轻质土过渡段范围内竖向加速度随着深度的增加呈减小趋势，且在基床表层范围内衰减速度最快。采用泡沫轻质土填筑过渡段路基与采用级配碎石和加筋土填筑过渡段路基均能够很好地使垂向振动加速度向下逐渐衰减，处理效果相当。

2）泡沫轻质土过渡段范围内竖向动应力随着竖向深度的增加呈减小趋势，在基床表层范围内衰减速度最快，且由普通路基段向桥梁方向过渡时基床表层动应力较由桥梁向普通路基段过渡时大。路基面以下5 m深度之后各断面动应力相对于路基面均衰减超过2/3。

3）两孔框架桥涵范围内桥面竖向动位移呈现出双峰分布规律，即桥柱顶面动位移较小，而两孔框架范围内动位移较大。列车上下桥两侧过渡段基床表层顶面动位移沿线路纵向分布规律及大小基本相同，动位移沿线路纵向靠近桥台大体呈现出递减趋势。采用级配碎石填筑与采用泡沫轻质土填筑过渡段基床底层对路基面动位移最大值影响差异不大，这说明过渡段范围内基床底层采用倒梯形填筑泡沫轻质土填料能够实现路桥平稳过渡。