基于能量平衡的扁平式恒力弹簧支吊架显式设计方法

杨露露， 邢庆果， 刚宪约， 孟 朋

(山东理工大学 交通与车辆工程学院， 山东 淄博 255000)

在油气、 热力管道系统中，通常需要几十米、 数百米甚至上千米输送管道，这些管道会因地面沉降、 承载波动以及环境、 介质温度变化而产生几十毫米甚至数百毫米挠曲变形。为了控制管道系统的热变形，需要采用管道支吊架对管道进行支承[1]。恒力弹簧支吊架是一种能够在一定行程内为发生竖直变形的管道提供恒定支撑力或悬吊力，而不会向附近管道或设备传递附加应力的装置， 因此在管道系统中垂直位移较大的部位，多采用各式恒力弹簧支吊架进行支承，以保证管道系统的安全运行[2]。

目前国内应用较多的恒力弹簧支吊架多为连杆式和主辅式结构。文献[3-4]中分析连杆式恒力弹簧支吊架的工作机理，给出了设计流程及强度校核方法。无论是三连杆式还是四连杆式恒力弹簧支吊架，相对于承载吊杆，结构都是不对称的，在运行过程中承载吊杆不稳定，使得整个装置的恒定度较低。主辅式恒力弹簧支吊架结构对称，运行稳定性好，恒定度较高。文献[5-6]中对比连杆式与主辅式的优点和缺点，总结了主辅式恒力弹簧支吊架的优势。文献[7-9]中根据主辅式恒力弹簧支吊架的工作机理，建立了主辅式恒力弹簧支吊架凸轮曲线的微分方程。文献[10]中从滚柱半径、转角简化、滚动摩擦力3个方面修正了凸轮曲线的微分方程。虽然主辅式恒力弹簧支吊架相较于连杆式有明显优势，但是在实际使用过程中也存在体积、质量、高度大并且安装位置受限等问题。

扁平式恒力弹簧支吊架是一种新型的恒力弹簧支吊架，相较于主辅式恒力弹簧支吊架，减少了竖直方向的主簧，具有结构对称、 紧凑，并且轴向尺寸、 质量、 安装高度小及恒定度高等优点，能够在实现为输送管道提供恒力支撑的同时，更好地适应安装高度有限的工程环境。凸轮是该类支吊架的核心部件，凸轮轮廓曲线的精度直接影响整个装置的恒力性能。

本文中建立扁平式恒力弹簧支吊架的力学模型，首先基于传统力矩平衡法推导凸轮曲线的微分方程，然后基于能量平衡法提出凸轮曲线的代数方程，并在此基础上考虑负载管滚柱半径的影响，建立凸轮曲线的范成修正方程，最后通过设计实例仿真，对比2种设计方法的设计精度，验证本文中提出的设计方法的可行性。

1 基于力矩平衡法的凸轮曲线微分方程

1.1 扁平式恒力弹簧支吊架结构与工作原理

扁平式恒力弹簧支吊架内部结构如图1所示，主要包括滚柱、 弹簧、 凸轮、 负载管等结构。由于凸轮曲线在全局坐标系中随着工作位置的变化而变化，在随体坐标系中的描述是恒定不变的，因此，采用全局坐标系描述各工作部件之间的几何关系和平衡方程，采用随体坐标系描述凸轮轮廓几何方程。选取右侧凸轮为研究对象，以凸轮转轴中心为原点，建立全局坐标系xoy和随体坐标系ηoξ。 全局坐标系以竖直方向为y轴，水平方向为x轴；随体坐标系以凸轮转轴中心到弹簧与凸轮连接点的连线为ξ轴，垂直于ξ轴的方向为η轴。

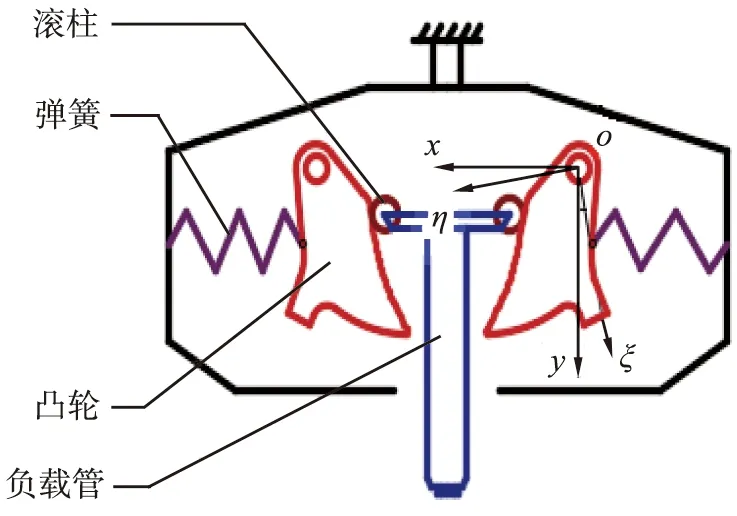
xoy—全局坐标系； ηoξ—随体坐标系。

在准静态条件下，负载管滚柱与凸轮的接触力(可以忽略切向滚动摩擦力)对凸轮转轴中心的力矩与弹簧力产生的力矩平衡，接触力的竖直方向分力等于负载管的恒力输出。随着负载管上、下运动，弹簧的变形和力单调变化，负载管恒力输出的关键在于合理设计负载管滚柱与凸轮的接触法向，即合理设计凸轮的轮廓形状，使每个接触点处的压力角α满足

Fsds-(Ptanα)dy=Pdx

，

(1)

式中：Fs为弹簧力；ds为弹簧力的力臂；P为恒力外载；α为接触压力角；dy为接触力水平分力的力臂；dx为接触力竖直分力的力臂。P、dx均为常数。

1.2 凸轮曲线微分方程推导

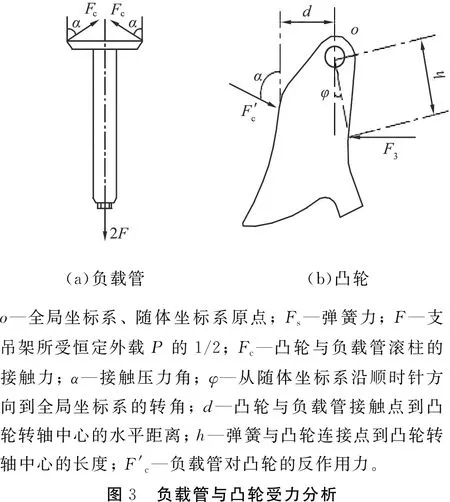
扁平式恒力弹簧支吊架为轴对称结构，如图2所示，取右半侧结构建立支吊架的简化力学模型，其中F为支吊架所受恒定外载P的1/2，Fc为凸轮与负载管滚柱的接触力，φ为从随体坐标系沿顺时针方向到全局坐标系的转角，d为凸轮与负载管接触点到凸轮转轴中心的水平距离，h为弹簧与凸轮连接点到凸轮转轴中心的长度。

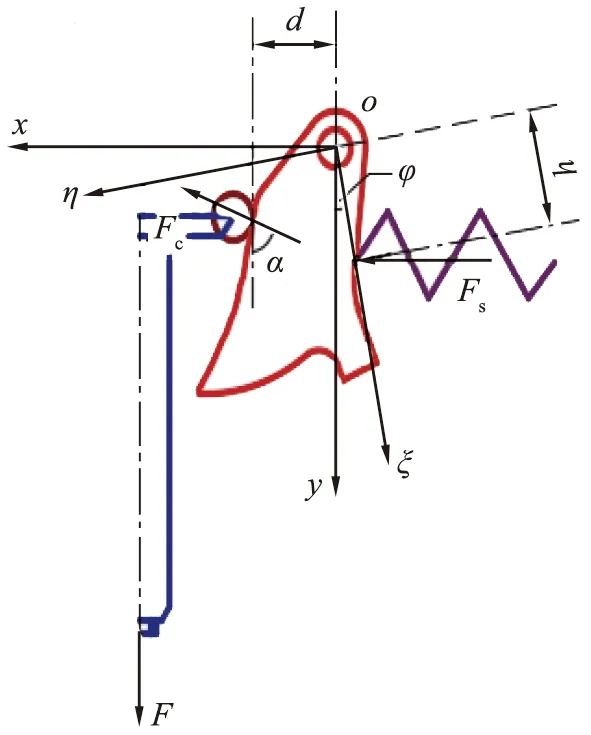
xoy—全局坐标系； ηoξ—随体坐标系； Fs—弹簧力； F—支吊架所受恒定外载P的1/2； Fc—凸轮与负载管滚柱的接触力； α—接触压力角；φ—从随体坐标系沿顺时针方向到全局坐标系的转角；d—凸轮与负载管接触点到凸轮转轴中心的水平距离； h—弹簧与凸轮连接点到凸轮转轴中心的长度。

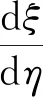
(2)

因此， 得到tanα、 tanφ关于η、ξ的表达式即可得到求解凸轮曲线的微分方程。为此，对支吊架进行几何关系和受力平衡分析。

1.2.1 坐标变换

简单起见，先假设负载管滚柱半径为0，则负载管与凸轮接触点到凸轮转轴中心的水平距离恒为d，因此，负载管与凸轮接触点的坐标在2个坐标系中存在几何关系

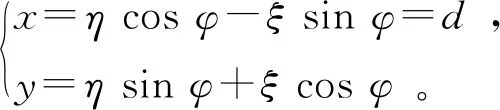
(3)

在恒力弹簧支吊架运动过程中， 凸轮摆动角度一般小于5 °, 满足小转角假设， 即有cosφ≈1， tanφ≈sinφ，则有

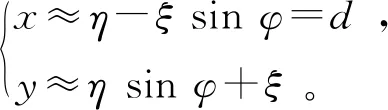
(4)

整理式(4)，可得

(5)

(6)

1.2.2 受力分析

图3所示为负载管与凸轮受力分析。对于负载管，y轴方向所受力Fy的合力为0，即有

∑Fy=0, 2Fccosα-2F=0

。

(7)

对于凸轮，弹簧力对凸轮转轴中心的力矩和负载管与凸轮接触力对凸轮转轴中心的力矩Mo之和为0，即有

(8)

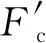
整理式(7)、(8)，可得

(9)

1.2.3 弹簧力

设弹簧刚度为k， 当凸轮转角为0时， 弹簧预压缩量为a， 则负载管运动至任意位置时， 弹簧力Fs为

Fs=k(a+hsinφ)

。

(10)

将式(5)、(6)、(10)代入式(9)，整理可得

(11)

将式(5)、(11)代入式(2)，即可得到凸轮曲线的设计方程为

(12)

该方程是关于η、ξ的一阶非线性微分方程，无法求得解析解，只能用计算机软件求解数值解。

2 基于能量平衡法的凸轮曲线显式代数方程

基于传统力矩平衡法推导的凸轮曲线方程为非线性微分方程，形式复杂，计算困难；推导过程中利用了小转角近似假设，导致设计曲线误差较大。本文中从能量角度考虑，提出一种基于能量平衡的扁平式恒力弹簧支吊架的凸轮曲线设计方法。

根据能量守恒定律，不计摩擦损耗，恒力弹簧支吊架在恒定外载P(P=2F)作用下发生竖直位移，支吊架外载做功与弹簧变形能变化量相等。

根据支吊架内部的能量转化关系，可得

2Fdy=2Fshcosφdφ

。

(13)

将式(10)代入式(13)，整理可得负载管垂直位移与随体坐标系转角的微分方程为

(14)

式中y0为转角φ为0时负载管与凸轮接触点在全局坐标系中的坐标。

对式(14)积分并整理，可得负载管垂直位移与随体坐标转角的代数方程为

(15)

方程(15)是关于y、φ的代数方程，推导过程简单，形式简洁，求解简便，减少了小转角假设的误差，计算结果更准确。

不考虑滚柱半径对凸轮曲线的影响时，利用全局坐标与随体坐标的坐标变换公式，即可得到求解凸轮曲线的方程为

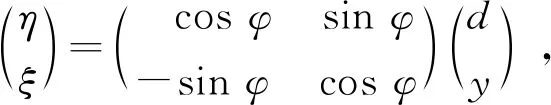
(16)

(η,ξ)即为所求凸轮曲线坐标。

3 考虑负载管滚柱半径的凸轮曲线修正方程

1、 2节中推导的方程均为假设滚柱半径为0时的凸轮曲线方程。当滚柱半径不为0时，以右侧凸轮为例，在恒力弹簧支吊架工作过程中，滚柱中心到凸轮转轴中心的水平距离恒为d，滚柱与凸轮接触点到凸轮转轴的距离始终小于d，利用范成原理，将式(15)、(16)求得的凸轮曲线沿各轮廓点的法线方向向背离负载管一侧移动半径距离，即可得到考虑滚柱半径的凸轮轮廓曲线，如图4所示。

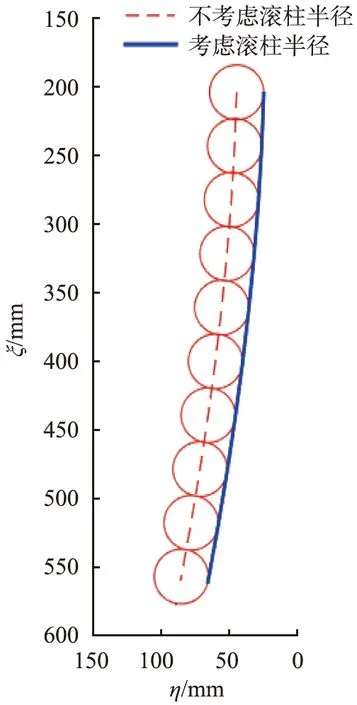
ξ、 η—随体坐标系ηoξ的坐标。

取图4中某滚柱图形放大绘制凸轮曲线沿接触法向的单位矢量，如图5所示。

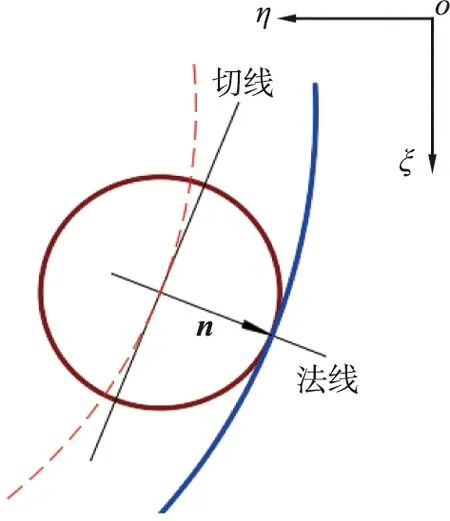
ηoξ—随体坐标系； n—凸轮曲线沿接触法向的单位矢量。

单位法向量为

(17)

将单位法向量n与滚柱半径r的乘积叠加至不考虑滚柱半径的凸轮曲线方程，即可得到考虑滚柱半径后的凸轮曲线修正方程为

(18)

式中(η1,ξ1)为考虑滚柱半径的影响求得的凸轮轮廓曲线坐标。

4 计算案例

假设某扁平式恒力弹簧支吊架承受的恒定外载P=10 kN， 有效行程为400 mm(凸轮曲线轮廓点与凸轮转轴中心之间的竖直距离为200～600 mm)， 弹簧刚度k=500 N/mm， 弹簧与凸轮连接点到凸轮转轴中心的长度h=400 mm， 凸轮转角为0时弹簧的预压缩量a=80 mm， 滚柱中心到凸轮转轴中心的水平距离d=60 mm， 滚柱半径r=20 mm， 假设滚柱运行到有效行程的中间位置时凸轮转角为0， 即有y0=400。 根据上述参数， 利用MATLAB软件求解凸轮曲线， 并利用Adams软件进行仿真校核。

4.1 凸轮曲线的计算

为了对比传统力矩平衡法与能量平衡法的设计方程，暂不考虑滚柱半径的影响，求解相同起点时2种方法所得凸轮曲线，如图6(a)所示。为了对比2条凸轮曲线的差别，绘制2条曲线在相同横坐标下的纵坐标差值曲线，如图6(b)所示。

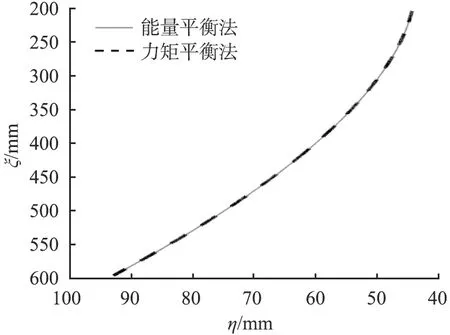
(a)凸轮曲线

由图6可知，2种设计方法在相同起点时所得的凸轮曲线形状基本相同，在相同横坐标点时的纵坐标差值的最大值约为0.08%。虽然曲线的差别很小；但是恒力弹簧支吊架的精度取决于凸轮曲线各点的压力角，因此微小的差别也可能造成较大的恒力精度差异。

在所得能量平衡法凸轮曲线的基础上，根据范成修正方程修正凸轮曲线，结果如图7所示。

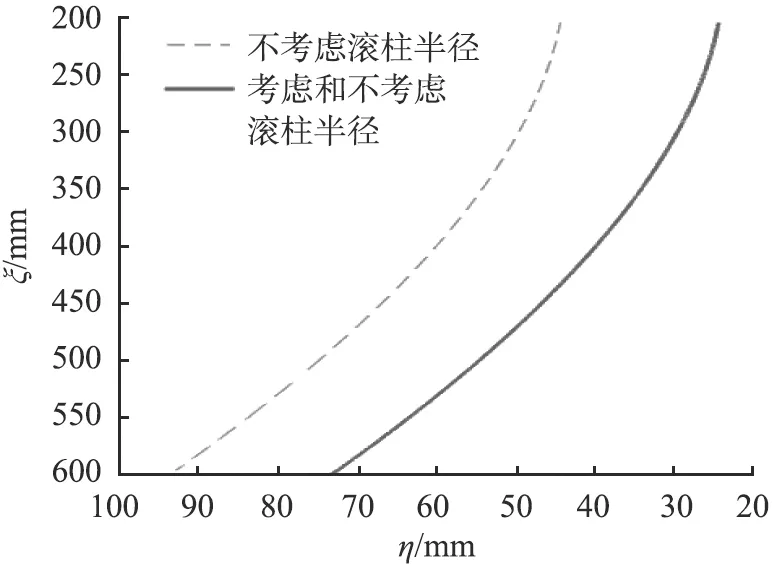
ξ、 η—随体坐标系ηoζ的坐标。

利用Adams软件建立恒力弹簧支吊架仿真模型，如图8所示。通过对负载管施加位移驱动，模拟恒力弹簧支吊架的工作过程，求解随位移变化的驱动力曲线。

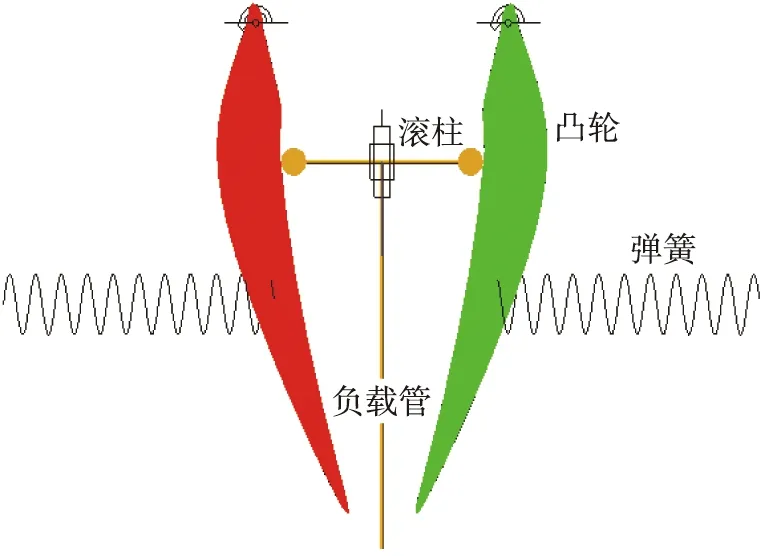
图8 恒力弹簧支吊架仿真模型

4.2 能量平衡法与力矩平衡法仿真结果对比

采用工作负载偏差作为判断恒力弹簧支吊架恒力性能的指标，工作负载偏差为恒力弹簧所提供的实际支撑力与额定外载的差值之比。

为了对比传统力矩平衡法与能量平衡法设计方程的精度， 对2种方法所求的不考虑滚柱半径的凸轮曲线进行仿真分析并进行数据处理， 得到工作负载偏差曲线， 如图9所示。 由图可知， 采用传统力矩平衡法设计的恒力弹簧最大工作负载偏差约为0.96%， 采用能量平衡法设计的恒力弹簧最大工作负载偏差约为0.53%。 由此可知， 基于能量平衡法的凸轮曲线方程的设计精度高于传统力矩平衡法的。

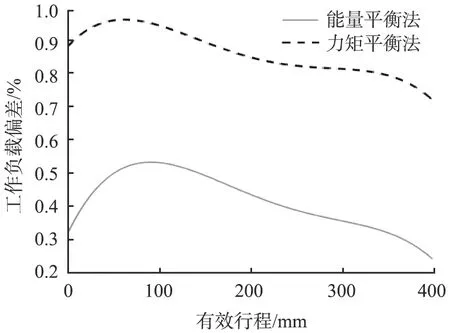
图9 传统力矩平衡法和能量平衡法的仿真结果

4.3 滚柱半径对设计精度的影响

为了验证本文中考虑滚柱半径的凸轮曲线修正方程的有效性，根据图7所示的考虑滚柱半径的凸轮曲线坐标点，对恒力弹簧进行建模仿真分析。考虑滚柱半径方法与传统的直接加滚柱半径的设计方法的工作负载偏差曲线如图10所示。由图可知，在不考虑滚柱半径的凸轮曲线的仿真模型中直接加滚柱半径仿真的最大工作负载偏差约为0.57%，设计时考虑滚柱半径所求凸轮曲线仿真模型的最大工作负载偏差约为0.31%。由此可知，设计时考虑滚柱半径对凸轮曲线的影响能进一步提高凸轮曲线的设计精度。

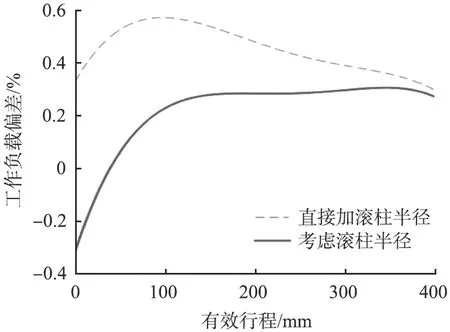
图10 滚柱半径对恒力精度影响的仿真对比

5 结论

扁平式恒力弹簧是一种新型的支吊架结构，既具有主辅式恒力弹簧恒力精度高的优点，又因取消主簧而大幅节省垂向安装空间。基于能量平衡原理，针对扁平式恒力弹簧支吊架凸轮轮廓曲线提出了一种显式代数方程模型，通过对比研究可以得到以下结论：

1)传统力矩平衡法得到的凸轮曲线方程为非线性微分方程，基于能量平衡得到的新模型为代数方程，推导过程中减少了小转角假设误差，计算更简单，精度更高。

2)利用范成修正方程建立的凸轮曲线修正方程，方法简单、高效，能够将滚柱半径对凸轮轮廓曲线的影响考虑到设计阶段。

3)实例设计分析对比表明， 能量平衡法新模型的设计精度明显高于传统力矩平衡法的； 考虑滚柱半径的范成修正方程能进一步提高支吊架的精度。