多频带带宽相参合成技术研究现状

张 硕，杨 君，葛鹏程，冯婷婷，杜 钰

(航天工程大学， 北京 101400)

1 引言

在空间作战、空间态势感知等军事应用中，需要借助雷达对目标的高精度一维/二维成像结果实现空间目标监视识别，获取目标的尺寸、形状、结构、运动等精细信息。一般情况下，要求对空间目标的观测信号带宽至少2 GHz以上，成像分辨力10 cm左右。因此，针对此类空间目标，尤其是空间碎片等小目标的精细结构通常小于距离分辨单元。而距离分辨单元与雷达的带宽成反比，为进一步提高分辨率的一个简单方法是升级雷达系统硬件以增加其带宽。但是通过这种将单部雷达的带宽设计的很宽从而提高分辨率的做法又面临着雷达带宽与威力性能、生产工艺水平、制作成本之间的矛盾。针对以上问题，一个更好的策略是求助于信号处理技术，比如说超分辨算法。通过对接收信号进行后处理来提高雷达分辨率，无需对原始雷达设备进行任何硬件修改。多频带带宽相参合成技术，就是将超分辨算法应用于多个空间并置的不同频带上工作的雷达的数据相干融合技术。该技术对多段子带回波进行相参合成，形成超宽带观测能力成为克服单雷达成像系统带宽局限的一种有效方式。该方法与传统方法相比，无需改变原始雷达体制和硬件设备，仅利用先进的信号处理技术就可实现雷达带宽和成像分辨力的成倍增长。在保证原雷达探测威力的同时降低了超宽带雷达研制难度和硬件成本，由此来看，多频带带宽相参合成技术具有极大的现实研究意义和学术研究价值。

在1997林肯实验室期刊发表了题为《Ultra-Wideband Coherent Processing》的论文[1]，成为最早开展多频带融合成像技术研究的实验室。该论文公开了暗室实验结果，展示出了多频带融合成像的巨大潜力，同时也拉开了多频带融合成像的大幕。在1999年，林肯实验室的Cuomo第一次公开发表了基于两部雷达回波数据的信息融合，成功的完成了真假弹头的辨别实验[2]，并首次阐述了多部雷达回波合成超宽带的关键性技术。由于雷达观测到的目标的回波在观测的频带上具有缓变的特性，因此多频带雷达带宽相参合成是可行的，可以用同一个回波模型来描述不同雷达的观测回波。因此，也可以认为不同雷达的观测回波是一个回波模型在不同频带上的观测结果。相参合成就是在一定的数据约束下，借助多段已知观测数据估计信号模型参数，再结合模型参数外推预测空缺频段数据，最后将所有频带的数据融合，等效为一部超宽带雷达的探测效果。在这个过程中，相参配准和带宽外推融合成像是需要解决的两个关键性技术。相参配准是将非相干的观测回波进行相干化，使其满足相参性，是该领域的难点和关键性技术之一；带宽外推融合成像是将配准后的多段回波数据进行外推融合，使其成为一个大带宽信号，从而得到探测目标更加精细的图像。

2 相参配准研究现状

1999年，Cuomo提出了一种用于不同频带上工作的多个空间并置雷达的数据相参融合技术。该技术首先将子带进行互相关运算以补偿不同雷达子带之间的相移，然后用一个全极点模型拟合稀疏子带的测量值，并用一种改进的求根多重信号分类(root-multiple signal classify,Root-MUSIC)算法估计其参数。最后，使用该模型对子带之外的数据进行外推和插值[2]。类似的,文献[3-4]对来自多波段空间分布的数据融合进行讨论，其中不同的雷达具有不同的工作频带，并在不同的角度位置照射目标。

实际上，上述的超分辨率算法采用了衰减指数和(DE)模型,也称为全极点模型或Prony模型[5-6]去拟合宽带雷达数据并用现代谱估计技术估计模型参数，如求根-MUSIC方法[7]、矩阵束方法[8]、ESPRIT方法[9]等等。这种解决方案主要有以下几个问题:

1) DE模型(全极点模型/Prony模型)并不能精确表示宽带的几何绕射行为，导致宽带雷达数据与模型之间不匹配，限制了超分辨算法的精度。

2) 模型阶数对算法性能有重要的影响，但Akaike信息量准则法(Akaike information criterion,AIC)和最小描述长度法(minimum description length,MDL)很难准确估计模型的阶数。

3) 大多数谱估计技术通常对噪声敏感，这抑制了它们在真实场景中的鲁棒性。

针对以上问题，学者们主要从参数估计和全极点模型的选择两方面进行了研究与改进。

2.1 基于模型参数估计的改进

2008年，为解决传统的基于改进的Root-MUSIC融合方法的极点不匹配问题，Ye F等[10]提出了一种基于频谱估计和幅度相位误差模型方法来补偿雷达子带之间的非相干，使用二维融合来改善分辨率，并开发了一种新的扩展矩阵增强矩阵束(extended matrix enhancement and matrix pencil，EMEMP)算法。同年，徐少坤等[11]将雷达的二维成像矩阵束算法引入到联合的多雷达观测融合成像上，并利用多雷达观测到的数据估计散射中心参数，从而提高了雷达成像的分辨性能。2009年，针对改进的Root-MUSIC的传统融合方法对噪声较敏感且存在模型极点失配问题。叶钒等[12]通过将MEMP(matrix enhancement and matrix pencil)的二维频率估计方法推广到稀疏数据域,并提出一种基于扩展矩阵增强矩阵束(EMEMP)的融合新方法。该方法首先以满足增强矩阵束算法的配对要求构造每一维联合增强矩阵，接着利用MEMP算法估计模型的极点并对极点进行配对，估计模型系数。最后，利用内插频谱融合成像。该方法在解决极点估计失配问题的同时，提高了模型参数的估计稳健性。2016年，邹永强等[13]为了弥补经典Root-MUSIC融合方法抗噪性能差的问题，提出了一种基于矩阵束算法的多频带信号极点估计方法。为了处理子带信号之间的互不相干，通过每个子带对应极点的关系来求解非相参参数。然后，引入一种以最小化信号差2范数为目标的迭代算法来减小信号融合误差。仿真数据表明了该方法在低信噪比下也能够获得较好的融合效果。2017年，B.Hussain等[14]提出了一种改进的自回归(auto-regressive,AR)相干稀疏带处理算法，针对前所未有的小分数带宽(2.2%)分析其增强AR算法的性能。通过使用基于光子学的多波段雷达保证波段之间的相干性，跳过[2]中提出的相位配准过程将计算成本降低了40%，并且还提供了2个子带极点的精确估计。另外，通过实现高斯-牛顿算法使得非线性回归与各极点相位的精确估计相结合，从而快速收敛到最佳拟合模型参数。

2.2 基于模型选择与参数估计两方面的改进

2005年，贺治华等[15]将基于衰减指数和模型的多重信号分类算法替换为可以精确描述高频电磁散射特性的几何绕射模型，对多重信号分类算法进行改进，利用特征分析方法的信号与噪声子空间正交特性,使改进后的MUSIC算法不仅能够精确估计目标散射中心位置,而且能估计散射中心类型,取得了不错的效果.2010年，Shao Ming等[16]提出了一种基于GTD模型的二维状态空间方法，用来估计超宽带条件下运动目标的散射中心参数，并最终取得了相对不错的精度。2013年，占荣辉等[17]在几何绕射理论模型下，分析雷达回波的稀疏特性，将参数估计问题转化为压缩感知理论中的稀疏信号重构问题,据此提出了一种基于压缩感知的2维GTD模型参数估计方法。在支撑区域内对散射中心的GTD模型参数进行估计,最后利用聚类方法和最小二乘算法对估计结果进行修正。有效改善模型参数的估计性能,提高散射中心类型参数的估计精度。2014年，Tian Biao等[18]主要针对稀疏子带融合成像给出了一种基于几何绕射理论(GTD模型)的高精度参数估计方法。考虑到各子带回波的不相干问题，采用了相干处理方法。定点模拟数据的实验结果表明，基于该方法的一维距离像和二维逆合成孔径雷达(ISAR)图像的分辨率优于各子带。

此外，Paul Berry等[19]利用稀疏重构技术，研究了通过相干合成窄带雷达数据获得非合作目标识别的高分辨一维距离像，提出了一种压缩感知的多通道雷达带宽拼接技术，探讨了存在相位误差情况下，使用修剪的正交匹配追踪(pruned orthogonal matching pursuit,POMP)算法和L1范数正则化解算器来解决稀疏频带带宽的拼接问题。仿真结果表明，相对于正交匹配追踪(orthogonal matching pursuit,OMP)和传统以及改进的L1范数正则化，POMP有着显著的性能提升。

以上方法大部分都是基于全极点模型的极点进行相参化，但这需要在正确估计子带全极点模型极点的基础之上完成。然而，此类方法在实际处理中依然存在着很难精确估计模型阶数，扩展目标散射点数目众多，可能大于可估计的极点数目的问题[20]。针对以上问题，TianJihua等[21]提出了一种新的现代谱估计的方法，即利用全相位快速傅里叶变换(All-phase fast Fouriertransform)算法和迭代自适应方法进行多波段雷达信号融合。该方法通过全相位快速傅里叶变换算法对各子带之间的不相干量进行补偿，然后将迭代自适应应用于信号融合的互相关子带测量中，从而有效的避免了极点估计问题，如图1所示的相位差补偿效果。

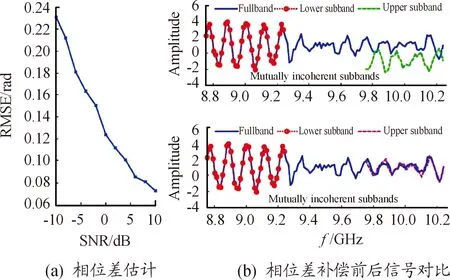
图1 相位差补偿效果曲线

除此之外，部分研究者受到Cuomo提出的将子带之间的非相参相位分为线性相位和固定相位两部分，对子带信号建立全极点模型，通过估计各子带极点的参数，并构建以非相参相位为变量的代价函数来求解线性相位项和固定相位项方法的启示。研究发现，雷达一维距离像间的平移量可以反应出线性相位项的差异，进而利用此关系求解线性相位项，定义代价函数求解固定相位项[22-25]。这类方法相比于以上方法而言，减少了一定的计算量，简化了算法。由于是先求取线性相位项并加以补偿，因此固定相位项的求取并不受线性相位项的影响，精度相对较高。但也存在一些问题，例如固定相位项的求取受到线性相位项求取精度以及定义的相干函数及全局搜索步长的影响很大。

3 融合成像研究现状

在相参配准(相干处理)之后，多个子带之间相互相干，满足了模型拟合的条件。对于多子带融合，模型拟合极其重要，因为模型拟合的精度决定了合成信号全频带的精度。林肯实验室的研究人员提出了一种超分辨率算法，使用所谓的全极点模型来拟合频率数据。传统研究工作者则在此基础上进行了改进，主要是建立全频带全极点模型。通过相参配准后的子带回波数据进行带宽外推和插值，补全空缺频段数据，从而得到融合后的全频带信号。

3.1 基于全频带全极点模型

2013年，田彪等[26]基于GTD模型提出了一种高精度参数估计算法，去解决多频带带宽相参合成的相参配准问题。这种方法通过来自不同频带的全极点模型中，中心幅度以及极点的相位差来估计不同频带的非相参量。利用缺损数据幅度相位联合估计方法对相参配准后的频带数据填补，最后再以补全后的全频带数据对几何绕射-全极点模型的参数进行高精度估计，得到融合以后的全频带数据。2014年，Zhang Huanhuan等[27]采用了一种类似于文献[1]的方法。首先用各个子带的全极点去拟合数据，然后利用相干函数拟合后的两个子带全极点模型进行相参配准；接着用基于GTD模型的参数构建冗余字典，快速稀疏贝叶斯学习算法来计算字典原子权重，以最终的权重和字典原子来测量子带并进行插值和外推。2019年，Xiong Di等[28]提出了一种用于多波段雷达信号融合ISAR成像的子波段互相关补偿方法，该方法将线性相位项和固定相位项补偿过程解耦。使用酉-旋转不变技术估计参数(unitary estimation of signal parameters via the rotational invariance techniques，U-ESPRIT)方法提高每个子带极点估计的精度，并仅使用与相同强散射体一一对应的每个子带的有效主极点，进一步提高了线性非相干相位的估计精度。此外，通过对每个子带信号应用基于相同旋转中心的相位自动聚焦方法来补偿子带之间的固定相位项，从而有效地补偿子带之间回波的初始相位差(固定相位项)。

由于全频带全极点模型实现的线性预测方法容易受到回波数据信噪比的影响，而且采用这类方法重构的分辨率往往不高。近年来，现代谱估计和稀疏信号处理技术的引入给多频带融合提供了更多优化的解决途径，有效的避免了传统方法对估计模型阶数精度的要求[21,26-27,29-32]。

3.2 基于稀疏子带表示

2013年，Bai Xueru等[19]基于稀疏子带表示，导出空间目标雷达成像的几何绕射信号模型，并介绍分析了可用方法。提出一种适用于高速运动空间目标稀疏子带成像方法，该方法包括距离和方位相位补偿、间隙数据填充、散射体数目估计、幅度估计和方位图像融合。最后，利用定点和电磁散射模型对模拟数据进行成像，从而证明此方法的有效性。2018年，Hu Pengjiang[33]针对逆合成孔径雷达成像领域，越来越多的小目标表征需求，提出一种新的稀疏子带成像框架。该方法首先对每个子带进行精细成像，通过精细成像补偿子带回波数据之间的高阶相位误差。然后进行梯形变换以统一子带的图像尺度，并对稀疏子带进行相干处理，执行跨距离压缩增强返回的稀疏性，以此获得可观的信噪比增益。最后，基于自回归模型对跨距离单元的压缩子带回波数据进行插值，通过平滑l0算法重建高分辨率距离像(HRRP)。该方法提出的框架不需要填充子带之间的空隙，并且对于带隙具有鲁棒性。

近年来的研究从原理和实践上证明，稀疏贝叶斯学习[31-32](sparse bayesian learning，SBL)等贝叶斯方法可以获得更好的稀疏恢复性能，广泛应用于波达角方向估计[34]和雷达成像[35]。在多频带融合成像应用中，与现有的参数谱估计方法(如Root-MUSIC和凸稀疏近似算法[27])相比，尤其是在恶劣的受限等距特性(restricted isometry property,RIP)条件下,SBL方法表现出优越的性能。

2017年，Ma Juntao等[30]针对稀疏孔径的多频段高分辨力成像，提出了一种基于波形融合字典的新方法，并进一步讨论了如何构造一维和二维融合字典，引入拉普拉斯先验的贝叶斯方法求解欠定方程。利用融合字典与多频段信号的匹配结构，避免了传统的基于快速傅里叶变换或者经典谱估计方法所带来的多频段融合的非均匀和带隙谱问题。因此，该方法不需要采样、插值或外推操作从而避免了更多误差的引入。2018年，Zhou Feng等[32]提出了一种基于贝叶斯学习的高分辨率稀疏子带成像方法，构建了概率模型并借助稀疏贝叶斯学习算法进行最终的融合成像。

4 技术难点

4.1 相参配准

相参配准是对非相干相位估计与补偿的过程，而非相干相位主要是指线性相位项和固定相位项。针对线性相位的差异估计方法较多，精度也较高；但是对于固定相位项的估计精度较低。然而，相参配准的难点就是对于非相参量的估计与精确补偿。具体的估计方法可以大致分为两大类：

1) 将多部不同频带雷达中的某部雷达的回波作为参考回波，其余回波乘以非相干量，共同构建一个雷达回波之间满足相干性的相干函数；并利用优化算法搜寻，求取非相干参量。此类方法的参数估计精度高，但仅适用于高信噪比条件，计算量大且容易陷入局部极小值。

2) 基于全极点模型的极点进行参数化，即利用线性相位差异在极点中而固定相位差异在幅度系数中的结论，结合MUSIC、ESPRIT、矩阵束法等参数估计方法直接估计子带模型参数，进而反推出线性相位项和固定相位项的值。这类估计方法需要在正确估计子带全极点模型极点的基础之上完成，而在实际处理中受噪声等因素影响很难精确估计模型阶数。此外，这类方法不适用于散射体众多的复杂目标。

现阶段，针对以上问题。文献[21]提出全相位快速傅里叶变换算法和迭代自适应方法进行多频带雷达信号融合。文献[37]提出了一种基于有效极点和相位自动聚焦的相干处理方法用于补偿多频带雷达信号融合成像中子带间的非相干相位。通过子带极点相位序列的最大互相关提取有效极点，然后重新排序,估计线性非相干相位；对于固定相位的估计，将各子带回波分别采用能有效补偿随机初始相位的相位自动聚焦算法，从而有效的消除了噪声对非相干相位估计的影响。仿真的结果验证了该方法的有效性和噪声不敏感性。如图2所示[37]，线性相位项估计误差随噪声的变化情况,其中A1为传统方法[36]。

图2 线性相位项估计误差的均值和均方根随噪声的变化曲线Fig.2 Variation of the mean and root mean square of the estimation error of the linear phase term with noise

4.2 融合成像

稀疏子带外推融合成像的最新技术主要包括：现代谱分析、稀疏信号表示以及稀疏贝叶斯学习。

1) 现代谱分析。现代谱分析的典型方法主要是间隔数据幅度和相位估计(gapped data amplitude and phase estimation,APES)为了实现精确的谱估计，可迭代优化几次直到收敛。此方法与传统的基于全频带全极点的参数谱分析技术相比，对模型失配和噪声具有更强的鲁棒性。但是，该方法在低信噪比下可能会引起较大的估计误差。

2) 稀疏信号表示。稀疏信号表示是将稀疏子带成像问题转化为稀疏信号重构问题。利用雷达观测目标散射中心的稀疏性，通过构建完备字典、求解线性方程等操作估计目标散射中心信息，进而重构信号的全局模型。该方法作为高概率重构信号方法存在失效的可能且迭代次数较多，计算量较大。

3) 稀疏贝叶斯学习。稀疏贝叶斯学习是通过构建适当的统计图形模型，在x轴上施加稀疏性促进先验，然后在贝叶斯框架中估计模型参数。例如文献[27]将高斯分布引入到x轴和噪声中并应用快速相关向量机[38-41]自适应地选择与数据相关的字典原子计算它们相应的权重。由于快速相关向量机算法具有从模型中删除基函数的操作，因此减少了矩阵求逆的计算负担。另一方面，算法的最佳收敛阈值随信噪比和散射中心的位置而变换，选择不当可能导致性能不佳，如幅度估计不足和散射中心重建不正确。

5 结论

从多频带融合成像研究的几十年发展历程来看，利用稀疏子带进行数据合成的高分辨率成像技术受到了广泛的关注。其中，稀疏贝叶斯学习等贝叶斯方法具有更好的稀疏恢复性能，逐渐应用于稀疏子带回波表示的多频带融合成像中。

但是，不论基于全频带全极点模型、谱估计方法还是稀疏信号处理技术的多频带融合成像处理方法，都更多的停留在利用仿真数据、单部雷达数据切分、微波暗室数据等手段验证融合成像方法的有效性。直到目前为止，还没有真正的多频带合成实地测量数据处理结果的报道。但是，实际的多频带带宽融合成像所遇到的问题较多，理论模型很难完全适用于实际情况且多部雷达的相干性要求更高等。因此，目前的理论研究成果并不能很好的应用到实际情况中。在接下来的研究中，应该更加注重复杂电磁环境下，多频带带宽合成技术目标仿真与验证以及实测数据的采集与应用，进而更好的指导实践。本文，对多频带带宽相参合成关键技术进行研究，并对其中最为关键的相参配准和带宽外推融合成像技术的技术难点与现状进行分类综述。