一种随钻密度仪的快速采样算法
2021-09-02余文钦
李 强,余文钦,余 凯
(中海油服油田技术事业部湛江作业公司,广东 湛江 524057)
随钻密度仪在测井作业过程中,由于受到自身旋转和眼井扩大两大因素影响,会产生偏心(仪器探测翼与井壁之间的距离),最终会造成泥浆对测量精度的影响。通常情况下,对于较小偏心,行业内普遍采用脊肋图对测量值进行校正,但对大偏心的情况,却没一种优化的方法。对于大偏心的环境影响,本文结合大偏心条件下的采样和数据处理,介绍一种由哈里巴顿公司使用的快速采样算法,其优点校正效果良好,同时也不需要其它测量数据参与校正,减少复杂性的同时,也避免引入其它的干扰因素。
1 偏心对测量的影响
仪器旋转产生的误差有两个原因:(1)肋线本身是非线性的,特别是在高对比度地层,高偏心的情况下。近源距和远源距探测器的平均零偏心和最大距离密度只有在这条肋线呈直线时才会相交在上面。(2)如果仪器以两种不同的计数率(R1和R2)采样,以获得0和1英寸之间偏心情况下的视密度。这些计数率计算出的密度值与每个计数率ln(R1)和ln(R2)的自然对数成比例。所以这些密度的平均值将与对数的平均值成比例,或[ln(R1)+ln(R2)]/2。然而,如果仪器旋转,用于获得旋转近密度和远密度的计数率是测量计数率的平均值,(R1+R2)/2,计算出的视密度与该值的自然对数成比例。如果两个值R1和R2不同,下面的数学式将不成立:
(1)
公式(1)的左侧与单个密度的平均值成比例,右侧与仪器旋转时测量的视密度成比例。因此,即使肋是线性的,由计数率平均值计算的远近密度的交会点也不会落在肋线上,并且会有旋转引起的误差[1-6]。
2 大偏心的统计校正问题
在图1中描绘了一条偏心达几英寸的低密度肋线。从脊线移开后,肋线最初表现良好,几乎呈线性,这部分用SOC(standoff correction)校正算法描述得很好。然而,在大约一英寸的位置处,肋线开始大幅弯曲,甚至在更大的位置,它实际上发生弯折并移动回脊线。对于大偏心时的肋线,其形状和范围是泥浆密度的函数。描述它需要更多复杂性的数学算法。更重要的是,一条肋线的曲率在大偏心时,会与另一个肋线在小偏心时相交。上述事实共同造成了在偏心大于1英寸时,使用脊肋图方法校正会出现既模糊又不准确的情况。
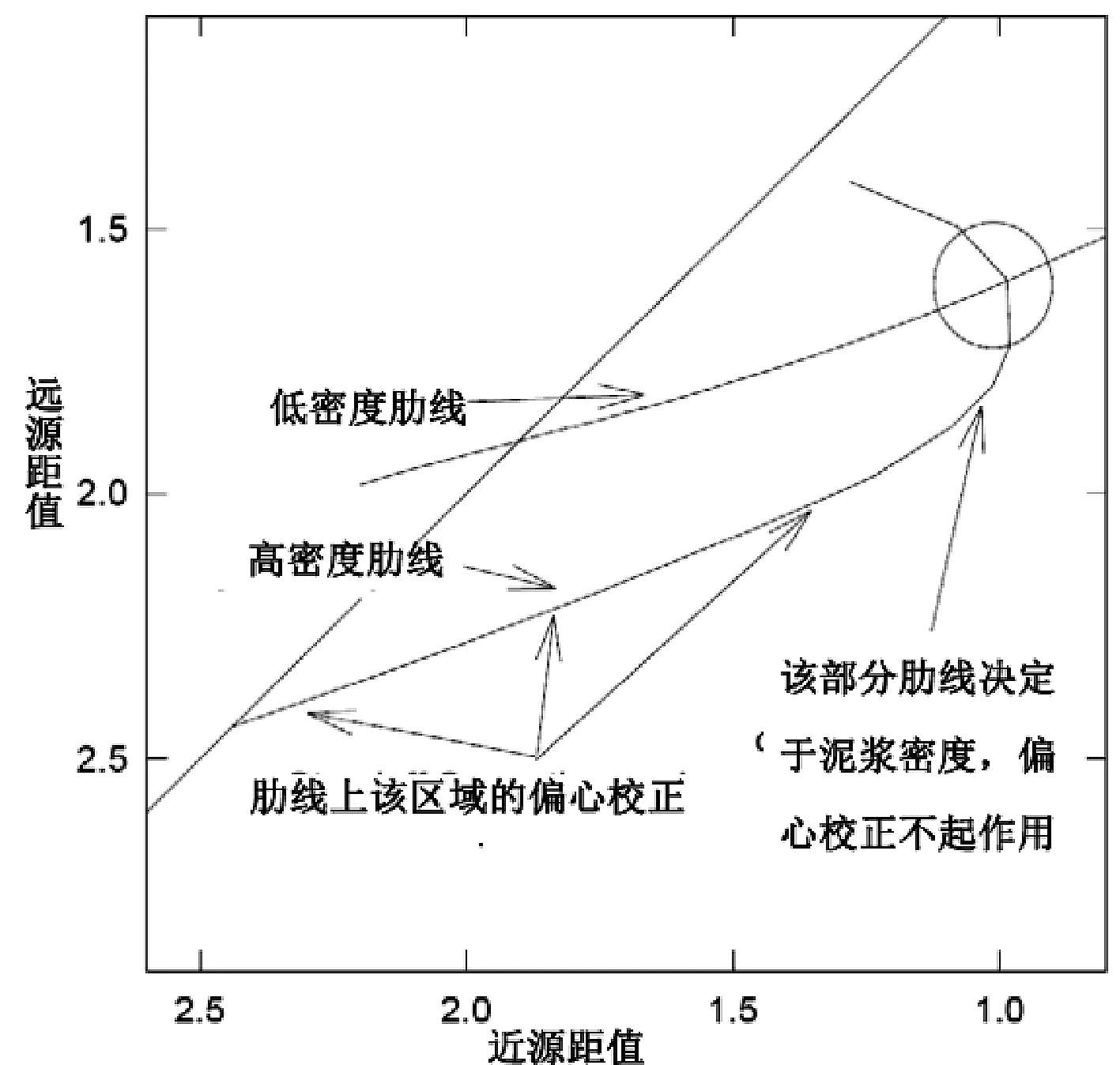
图1 脊肋图上的长短源距在多地层密度下的交会图Fig.1 Illustration of multiple formation density values on Spine/Rib cross plot
原则上,在井眼中随钻测井可以获得准确的测井曲线,因为通常在旋转过程中扶正器至少有部分时间与井壁贴靠。然而,必须使用一些方法来区分小偏心和大偏心的数据。目前有几种方法可以解决这个问题。一种是在斜井钻进时使用仪器面指示器。另外,可以用声波装置连续监测间隔。这两种方法都有一些可能的失效模式。如果仪器在井眼内转动,那么工具面法就会失效,这在垂直井眼中很可能发生,在斜井中也可能发生。随着泥浆比重的增加,声波法测定井壁间距变得更加困难,而且它可能会由于井眼中的岩屑或由于来自井壁反射的声波信号的倾斜反射而失效。
哈里巴顿公司采用的方法是根据探测器的计数率随偏心而改变制定的。在仪器旋转的时间尺度上检测计数率的变化,这些变化是由于偏心的变化造成的。
此方法的目的是从将小偏心的数据从大偏心的数据中区分出,由于它是纯粹的统计数据,它的优势是不需要额外的传感器的数据输入[1-2,6]。
3 快速采样算法原理
哈里巴顿公司采用的用于校正大偏心的密度测量,被称为“快速采样算法”。该方法的第一步是将通常持续时间在10~30秒之间的常规采样周期划分为大量较短(“快速”)的采样。第二步是确定哪些“快速采样”是在仪器靠近井壁时获得的,哪些是在仪器远离井壁时获得的。一旦确定,就可以确定在井壁附近采集的近、远源距的平均计数率,并像以前一样使用SOC校正方法计算出校正后的密度。
为了理解在大偏心和小偏心时的采样是如何被区别对待的,以图2所示的数据为例。这些数据是在一个石灰岩测试井的扩大井眼内,使用具有快速采样算法仪器采样得到的,仪器可在不到一秒的时间内获取“快速采样”数据。图2的上半部分显示了仪器非旋转情况下的采集数据,在图的下半部分显示仪器旋转时的数据。
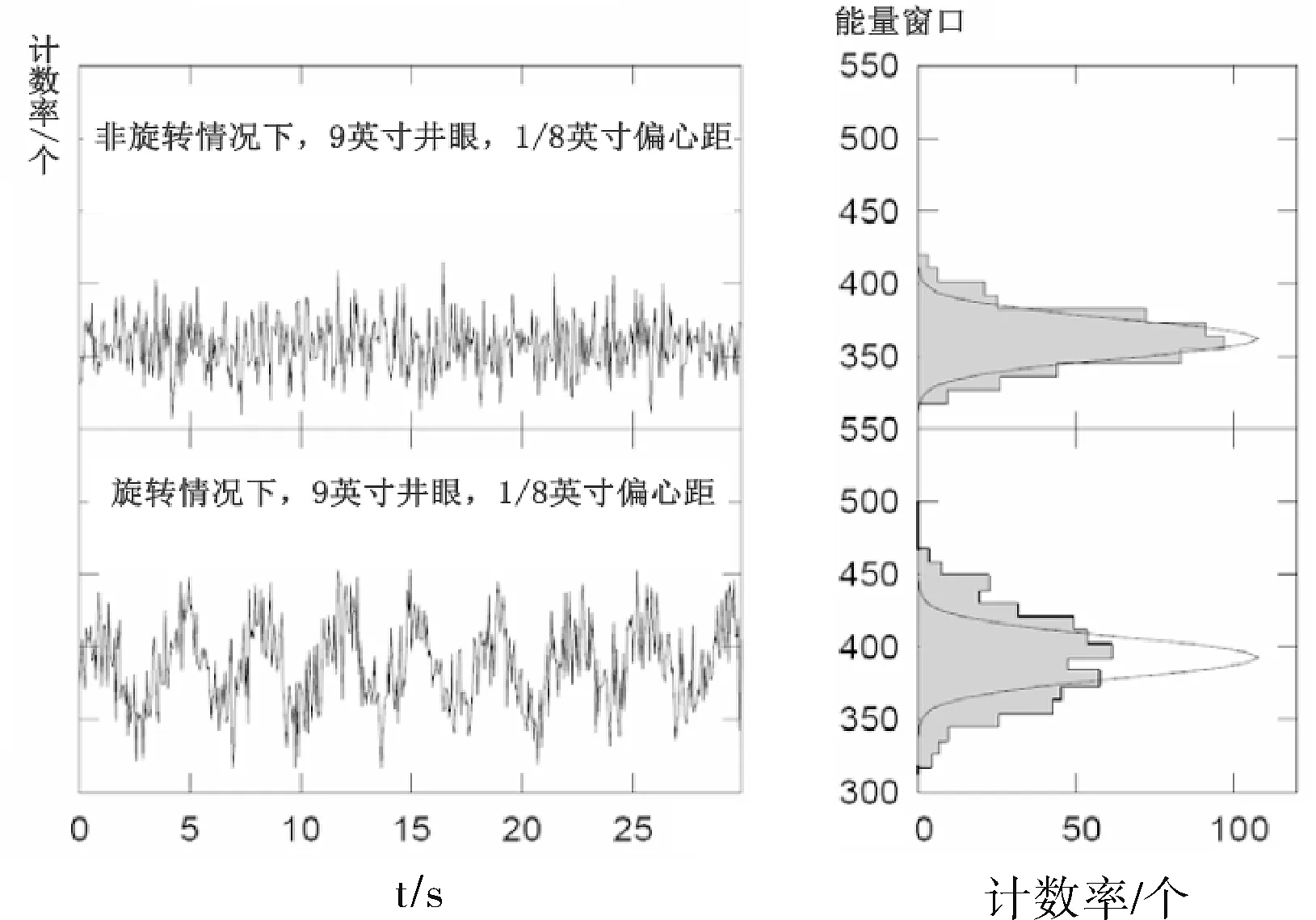
图2 快速采样时间序列和分布Fig.2 Rapid sample time series and distributions
静止数据和旋转数据分别以两种方式显示。首先,每个连续快速采样中的计数随时间的增加被绘制出来。数据中明显的噪声反映了核计数过程的随机性。
在右侧显示了两条曲线,第一是直方图,它是采样数量分布与每个采样计数的函数关系;第二是基于统计理论的采样预测分布图。核计数统计理论有提及,统计噪声仅取决于计数率,核计数统计是分布中噪声的主要来源。当仪器没有旋转,只是沿着均匀的井壁滑动时,或者当仪器在密度均匀且尺寸标准的井眼中旋转时,都可能出现这种情况。
通过将时间序列的预测分布与实际分布进行比较,可以确定偏心是否在变化。通过比较预测分布和实测分布的宽度,简单地进行比较。对于预测分布,宽度是每次采样的平均计数的平方根。当计数统计是造成测量分布中噪声的唯一原因时,这就会被证明与测量分布的标准偏差相同。当时间序列中有另一个噪声源时,标准差大于每次采样的均值计数的平方根。这两个数值都很容易在井下计算,通过对比可以很好地判断是否需要快速取样。
因此,在井下软件中,第一个任务是确定是否发生了偏心变化。如上所述,监控实际分布和预测分布的比率可以做到这一点。一旦确认间隔是变化的,低偏心数据将被隔离,以便单独用于密度计算。由此得出,正确的计数,也就是偏心最小的数,是分布在的一个极端或另一个极端上的数。
为了使用低偏心的采样计数,必须推导出一种方法,通过该方法可以在井下软件中确定分布中的极端计数。在此之后,必须确定小偏心下的各个近和远计数率[6]。
4 快速采样算法具体方法
回到快速采样过程的开始,并补充更多细节,将整个过程分解为一系列步骤,并依次讨论每一个步骤。该算法将在图3的例子中以数据为背景加以说明。
将一系列快速采样的近、远能谱存储在暂存存储器中。第一步是将每个快速采样时完整近、远能谱存储在仪器存储器的“高速暂存”区域。“典型”的情况可能包括在30秒内获取多个100毫秒的快速采样值。这将产生300个近源距和300个远源距的能谱,每一个都将存储在“高速暂存”中。在进行分析之前,必须获得完整的时间序列。
从存储在高速暂存内的能谱中定义一个要分析的时间序列。这指的是图3所示的时间序列。在实践中,从三个时间序列中做出选择:使用远探测器的总计数构建的时间序列;远探测器高能部分的计数构建的时序;或者是远探测器低能量部分的计数构建的时序。
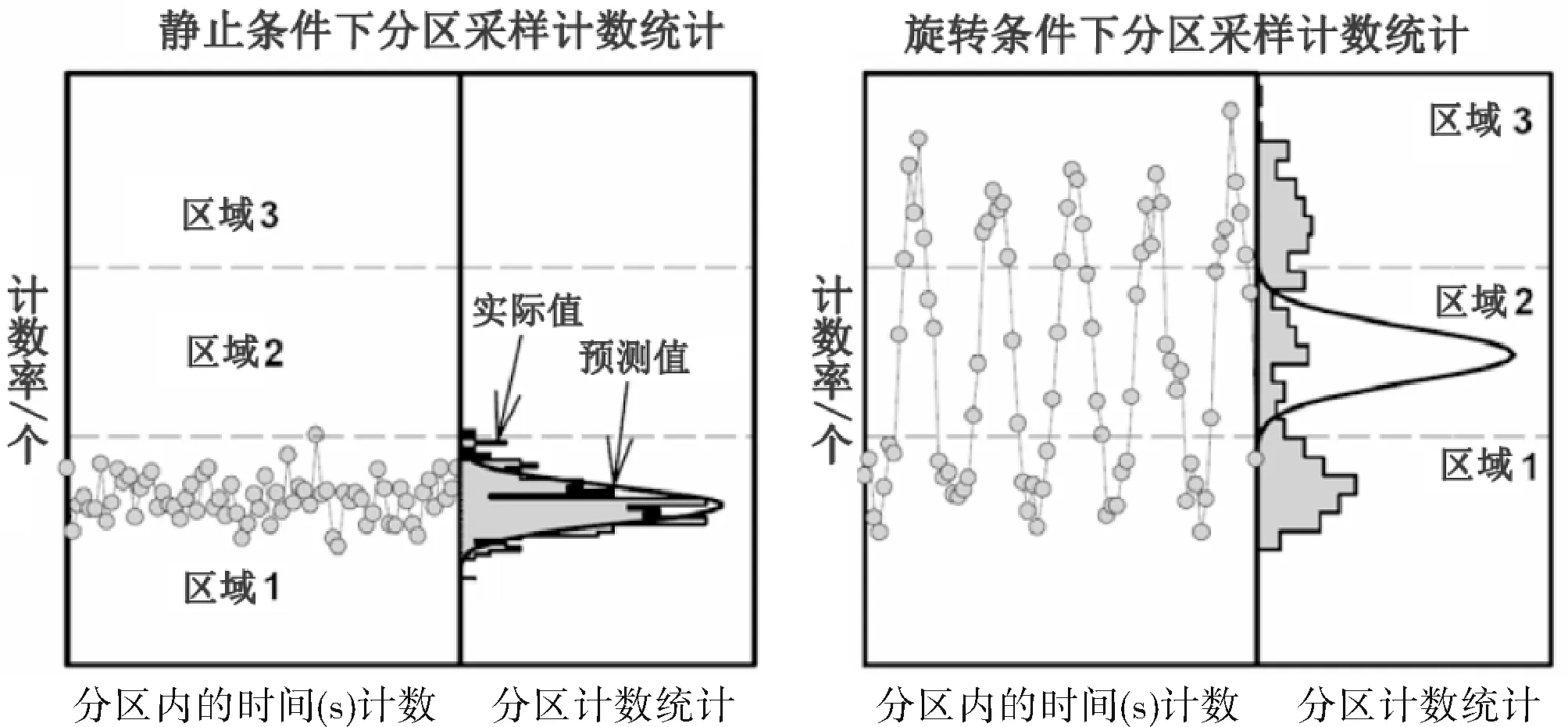
图3 静态和旋转条件下区域中的时间序列和分布Fig.3 Time series and distributions with bins under the stationary and rotating condition
将时间序列划分到多个区域内来,在这些区域中再对时间序列采样进行分类。在此步骤中,必须根据计数率将时间序列分布划分到多个区域内。图3中显示了对时间序列进行排序而定义的三个区域边界。可以看出,落到区域 1中的点包含所有与静态分布相对应的点。区域3中的点对应于在最大偏心附近的采样,其余的点都在区域2中。区域的边界和宽度是相对于分布的极端定义的。
根据各自的时间序列采样值,将近能谱和远能谱分配到区域。每个时间序列采样都是从同一个快速采样中取得的,该采样完整的近、远能谱已经记录在了高速暂存区内。首先确定每个时间序列采样落入的区域,然后该采样的近能谱和远能谱被分配给该区域。
计算每一个区域内密度窗口下和Pe窗口下的平均近、远计数率和视密度。现在,这三个区域中的每一个都有一些指定的近能谱和远能谱对。在传统的方法中,采用不同能量窗口的计数来确定密度和Pe的测量。
对每对远近密度对进行脊柱和肋骨矫正由于区域1和非旋转测量的结果几乎落在同一根肋骨上,当对它们进行脊柱和肋骨矫正时,它们产生的矫正密度几乎相同[1,6]。
5 井下和地面软件补偿
图4给出了快速采样测井段,以说明该技术的具体应用,以及影响快速采样测井精度的一些因素。测井实例取自一口地层较软,容易迅速冲蚀的井。钻头尺寸为12 1/4英寸,扶正翼直径为12英寸。图4显示了几个关键特性:

图4 快速采样算法测井曲线图Fig.4 Rapid sample log
曲线1显示了实际和预测的快速采样计数率分布的标准差之比,如上所述。这通常被称为标准差比(SDR)。它以相反的比例绘制,当它的值超过1.2时用阴影表示。在5010到5045英尺之间,工具没有旋转,导致SDR下降到接近1,快速采样算法被禁用。
曲线2和3,显示低计数率快速样品密度与传统密度。在冲蚀区间,两种密度是不同的。常规密度比快速取样密度受井筒流体的影响更大。
曲线3显示与低计数率、快速采样密度和常规密度相关的soc值。低计数率的快速样品密度与常规密度相对应距离较小,这表示计算值也较小。当井眼增大时,曲线之间的分离也越大。在滑动区间,两条曲线都显示出很大的值。这可能是由于仪器的方向偏离了井眼的低侧。在这段时间内,计算出的密度,无论是快速取样还是常规取样,都应谨慎处理[1,4]。
6 结 论
通过说明随钻密度测井仪在测井过程中的真实状态,详细分析偏心对地层密度测量的影响,深度认识旋转造成测量偏差的具体原因,可以让读者更加清晰的了解密度仪器在实际工作方式,而并非与仪器在静态条件下是相同的。针对大偏心下的数据处理,介绍哈里巴顿公司的快速采样算法,通过剖析算法,可以透彻的了解仪器的工作过程和数据处理方式,为目前在随钻密度测井过程中,在大偏心情况下测量数度普遍存在精度不高的问题,提供了一种有效和便利的算法选择。
