基于遗传算法的温度传感器布置优化

修晓波，李伯全，周 峰

(江苏大学 机械工程学院,江苏 镇江 212013)

链篦机—回转窑—环冷机是一种钢铁冶炼工艺设备，其中链篦机主要用于对生球团的干燥和预热。链篦机是一个大型、复杂的机电运动装置，其干燥过程温度空间分布复杂，难以实现精准的自动化控制。链篦机可以分为3个部分：鼓风干燥段、抽风干燥段、预热段[1]，其中鼓风干燥段(Updraft Drying，UDD)主要用于除去生球团的附着水。如果温度场不满足水分干燥的要求，球团在干燥过程中可能会发生爆裂，致使生产质量下降[2-3]。温度分布特性检测对于实现UDD温度精确稳定的自动控制是不可或缺的。

温度空间分布很难直接测量，通常研究多个单点式或超声温度传感器构成传感器测温阵列，进而采用插值或拟合的方式获取温度场信息[4-5]。在工业现场中，接触式单点测温传感器如热电偶、热电阻最为常用[6]。这种传感器的安装需要在设备上进行开孔。传感器布置过多，意味着需要在被测设备外壁开更多的孔，增加漏气风险，还会造成传感器数据冗余，成本提高。但布置传感器的数量不足又无法充分描述温度场的空间分布信息，对于温度控制的精度有较大的影响。因此，要获得UDD的温度场分布情况，就要对传感器数量和测点位置进行优化，利用数量和位置信息进行温度场重构。

插值和拟合的温度场重构方法直接影响温度场重构的精度。非线性最小二乘法[7-9]由于简单高效故而被经常采用。研究者发现，采用径向基函数(Radial Basis Function，RBF)的方法，可以有效提高重构的精度[10]，且适用于复杂函数。在温度场检测并进行重构时，通常不考虑传感器的布局优化问题，而是根据测温传感器和被测温度场的物理特性进行布置，例如采用均匀的传感器布置阵列来尽可能多地覆盖被测区域[11-13]，进而通过重构算法得到温度分布情况。采用计算流体动力学(Computational Fluid Dynamics，CFD)模拟温度场，根据温度分布趋势布置传感器[14]。对子区域进行划分，在每个子区域布置传感器后利用反距离加权的方式得到温度分布来有效提高其温度场的重构精度[15]。基于本征正交分解(Proper Orthogonal Decomposition，POD)并结合CFD[16-17]，给出确定传感器位置的目标函数，提升了计算速度，但其忽略了不同重构方法对于不同传感器布置方案的影响，所得结果存在较大的系统误差。

在工业现场中，温度场大多是动态变化的，但传感器的位置不能变化，导致温度场的描述具有一定的局限性。为寻找一组可以描述温度场分布特征的传感器位置，建立UDD温度场模型，利用CFD进行求解，得到干燥效果最佳时的期望温度分布。本文提出了一种用于确定传感器位置和数量的目标函数，采用遗传算法(Genetic Algorithm，GA)进行求解得到结果。本研究模拟了温度检测过程，得到不同位置温度值，根据RBF的方法重建温度场，并在最后分析该方法的有效性及误差。

1 传感器布置优化的数学原理

1.1 UDD期望温度场模型

UDD内的温度场主要由气体温度场和球团料层温度场两部分构成。球团料层温度场无法直接检测，因此只针对空间气体温度场进行研究。热风由UDD下部向上鼓入，经过球团料层进行干燥，干燥后的废气通过烟罩直接排出。在UDD中，影响干燥效果的气体温度主要取决于长度方向和高度方向的分布情况。因此本文将UDD作为一种二维温度场进行研究。气体在篦板下部和球团料层上部的主要换热方式为对流换热，球团料层为主要的传热传质区域。气体在链篦机内部的流动及换热过程可以由以下微分方程描述[18]。

连续性方程为

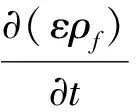
(1)

动量方程为

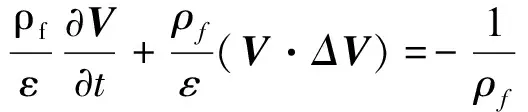
(2)

能量方程

(3)

式中，ε为球团料层孔隙率，取0.39；V为气体表观速度；vε为气体有效粘性系数；ρf表示气体密度；p为气体体积平均压力；Cf为气体比热容；kf为气体导热系数；hfs为气固对流换热系数；Afs为球团比表面积；Ts为球团表面温度；Tf为气流温度；Sfc、Sfm和Sfh分别为连续性方程源项、多孔介质阻力源项和气体能量方程源项，只发生在球团与热气流交换过程中，在空间内则无该项。

1.2 RBF温度场重构

RBF一般用于解决多元插值问题，并且已被证明可以以任意精度逼近任意函数[19-20]，适用于UDD温度场的重构。

设在二维空间布置有Ns个热电偶传感器，其中第i个测点温度Tf(xi,yi) 中xi和yi分别为沿篦床行进方向和高度方向上的传感器布点坐标。第i个传感器可以作为径向基插值的中心，其中径向基函数可以定义为下式[21]

(4)

式中，σ为径向基函数的形状参数，与传感器的布置位置有关

(5)

式中，dmax为传感器测量点之间的最大距离。

为获得温度在二维空间的分布特性，采用径向基函数对测点进行插值，即

(6)

式中，TRBF为使用RBF重构的温度场；λ、b、a为待定参数，且可由下式得到

(7)

其中，

1.3 温度传感器布置优化目标函数

温度传感器的位置和数量不是固定的，在实际检测过程中有很大的灵活性，且这些位置和数量的信息影响着重构的精度。为了尽可能提高温度场重构的精度，本研究构造了一个目标函数来描述重构温度场的精度，即

(8)

式中，n为总采样点数，与UDD的长度和高度有关；j为第j个采样点；n=hl/Δd2，Δd为采样精度，取值 0.01 m；h为UDD的高度；为UDD长度；e为目标函数，当e最小时，所得到的解为传感器最佳分布的二维坐标组合。

1.4 遗传算法设计

对于式(8)，方程的解为多传感器位置坐标的组合。根据采样精度的不同，其组合的数量也不同。随着采样精度的提高，其解的组合数量呈指数形式增加，难以求得准确解。GA是一类借鉴生物界进化规律演化而来的随机优化搜索方法[20-21]，是解决这种多目标优化的一种方案。GA通过对染色体的翻转、移位、交换等操作改变种群，通过不断选取最优解再遗传到下一代，最终得到一组方程的近似最优解。这个解可以作为温度传感器布置的最佳位置。GA的过程可以描述如下：(1)生成初始解；(2)第一组解由选择算子选择；(3)父解的后代由交叉算子创建。通过选择，不断进行优化，最终求得收敛结果。GA的参数设置如表1所示。

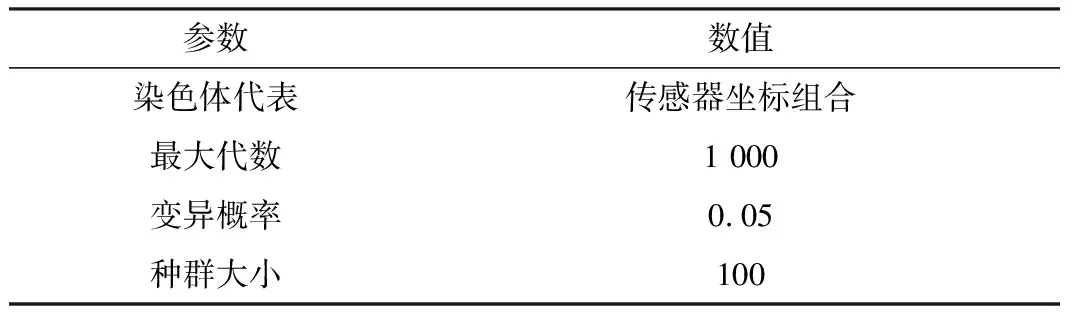
表1 GA参数

基于对UDD的结构特点分析，选择了一组可行的传感器数量组合，其中Ns分别为14、16、18、20、22、24个传感器。对理论温度场进行重构，还需要模拟温度测量的过程，即在UDD的外壁上随机布置一些测量点采样。这里的第一次随机采样为Ns个坐标点(xi,yi)，i=1,2,…,Ns，采样点的温度值为Tf(xi,yi)，i=1,2,…,Ns，使用这些坐标点进行温度场的拟合。

在GA求解中，由于坐标x和y是相互独立的，并且取值范围也不同，所以需要分开处理。分别取Ns个x和y，按变异概率，随机取一段“基因”进行以下4种操作：(1)保持(Hold)，即遗传原有的最佳染色体；(2)翻转(Flip)，即某一段基因逆序排列；(3)交换(Swap)，即交换某两个基因点；(4)滑动(Slide)，某段基因序列不变，循环右移一位。

2 UDD温度场模型求解

图1为UDD结构示意图。热气流从UDD下部被鼓风机鼓入，经过电动蝶阀和流量计，进入UDD内，在压力作用下穿过篦床和球团料层，对生球团进行干燥。干燥球团料层后的废气携带水蒸气从UDD上部的烟罩排出。为检测UDD的温度分布情况，可以在外壁上选择温度传感器布点进行测量。

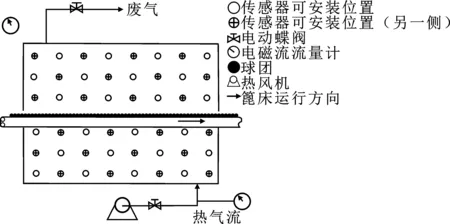
图1 UDD结构示意图Figure 1. Schematic of UDD

图1中， UDD温度场可视为二维分布，忽略宽度方向的变化，所以可以在UDD的两壁上布置温度传感器。图中标注的传感器布置位置只是一种预案，具体安装位置需要按照优化后的布局来设计。

链篦机按球团产量的不同有各种不同的规模。本文研究对象选择UDD的长度为9 m，高度为4 m，球团料层高度0.2 m。设置UDD边界条件，对式(1)～式(3)进行求解，计算得到UDD的理论温度场如图2所示。由于在UDD的边界无法布置温度传感器，因此在长度方向和高度方向上截取了部分温度场进行研究，长度为7.4 m，高度3.4 m。

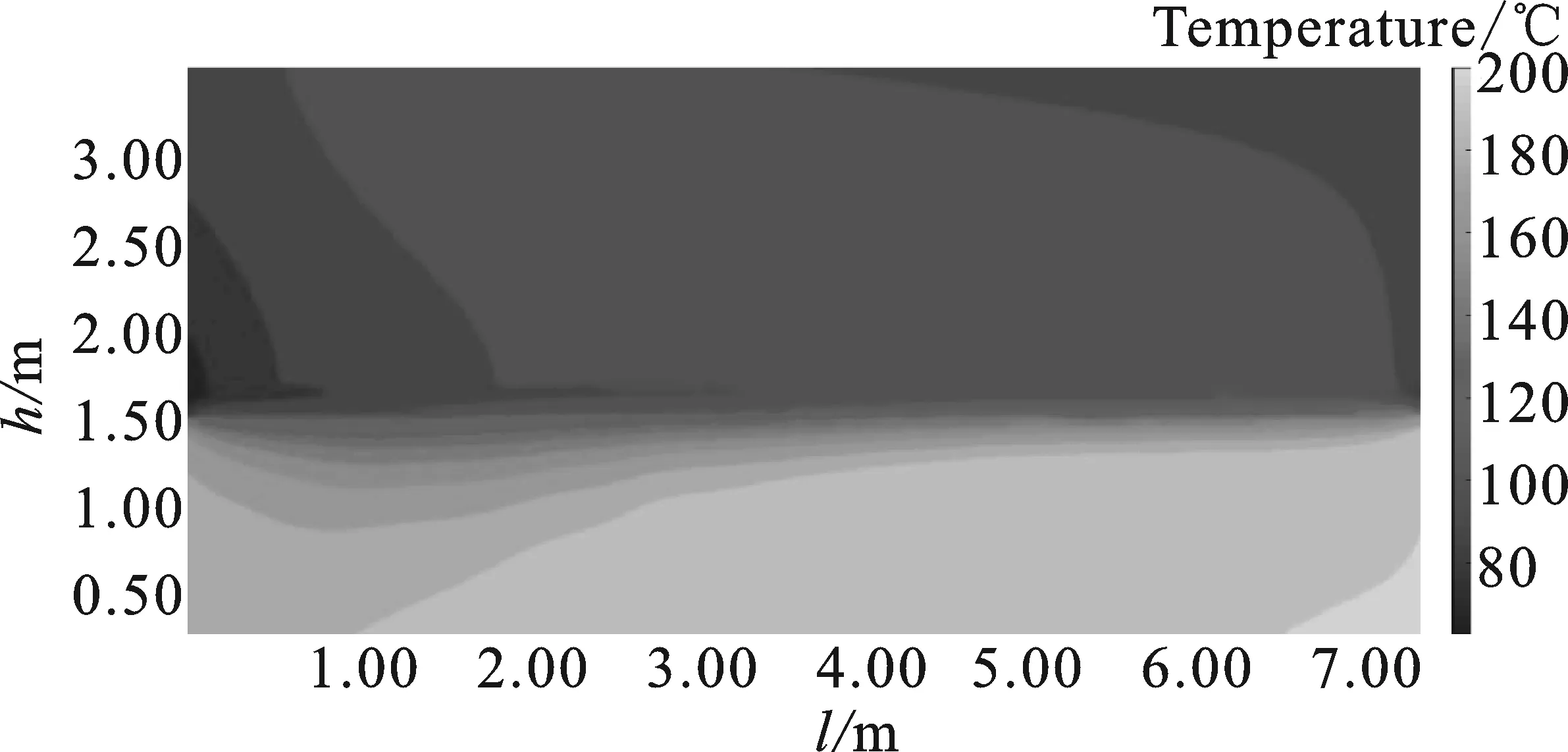
图2 UDD理论温度场Figure 2. Theoretical temperature field of UDD

3 测量温度场的传感器布点

3.1 GA求解结果

使用GA对不同数量传感器的布点位置进行求解，图3给出了不同数量下传感器优化的子代数与适应度e的关系。图3表明，GA在求解到400代之后已经渐趋收敛。

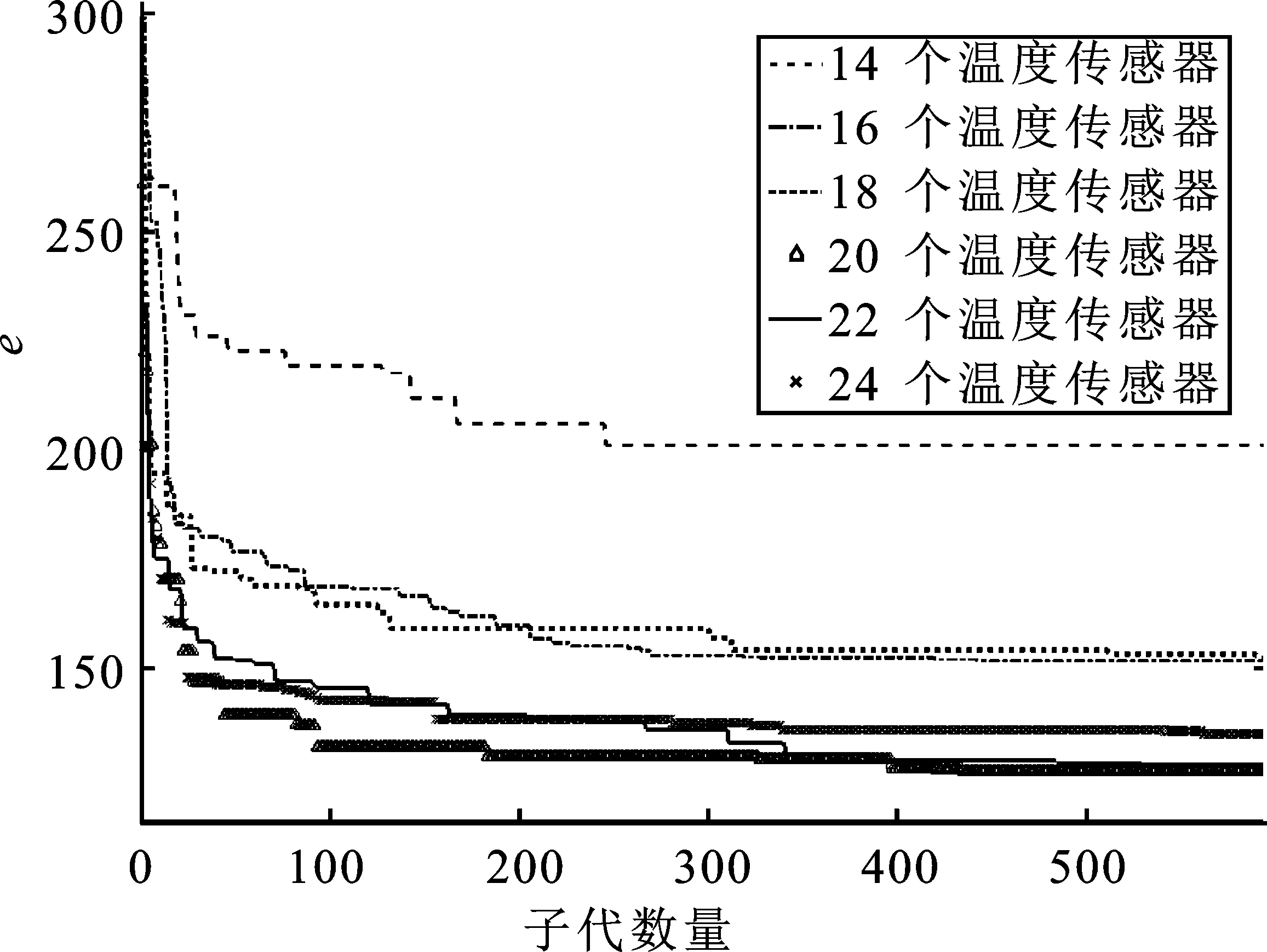
图3 适应度随迭代数量变化曲线Figure 3. Fitness according to GA generation

为了验证基于遗传算法传感器布置方法的效果，设计一组检测UDD温度场时传感器均匀布置的试验作为对照组。为覆盖尽可能多的位置，根据UDD的尺寸等间距布置温度传感器，作为未优化的传感器布置方案。图4为不同数量传感器重构温度场时的平均绝对误差折线图。图4的结果表明，并不是布置的传感器数量越多，就能得到更佳的测量精度。这是因为少量的传感器已经能够获得足够的拟合温度场分布信息，增加传感器的数量可能会导致数据冗余，即产生了无用的参考点。传感器数量少于22个时，随着温度传感器布置数量增加，其曲线呈现下降趋势，说明此时均匀布置传感器增加，则获取的有效信息点也增加了，精度也随之提高。

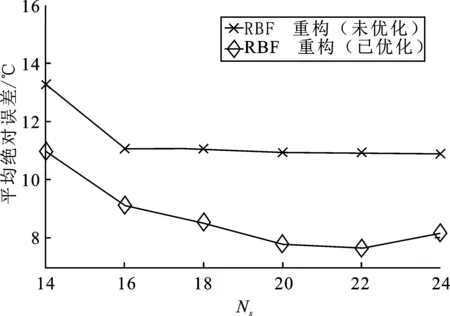
图4 不同布点数量下的平均绝对误差Figure 4. Average absolute error of different number of points

在温度传感器布置数量相同时，优化传感器布置后的误差普遍低于均匀布置时的情况。其中，优化后的温度场在采用22个传感器时达到了最低不确定度。采用RBF重构温度场后，优化后的温度场平均绝对误差较优化前提高了30.90%。如果未对温度传感器进行优化，则在16～24个传感器中的平均绝对误差差别不大。

根据上述结果，本研究给出以下布置温度传感器的数量选择：在UDD的温度场检测中，温度传感器的数量采用22个时能够使精度达到最佳。均匀布置传感器则可以采用16个。

3.2 温度传感器位置的确定

确定温度传感器的数量后，即可通过式(8)计算其最佳布置位置。图5(a)为22个传感器均匀布置时的点位图，其中(0.05,3.40)和(7.40,0.35) 两个位置用于检测出口和入口附近的气体温度。图5(b)为采用 RBF 方法重构的温度场云图。可以发现，在1.5 m以下时，有部分温度场保持了与理论温度场相似的趋势，但在篦床的入口处仍有较大的低温部分，与理论温度场存在较大的差异。

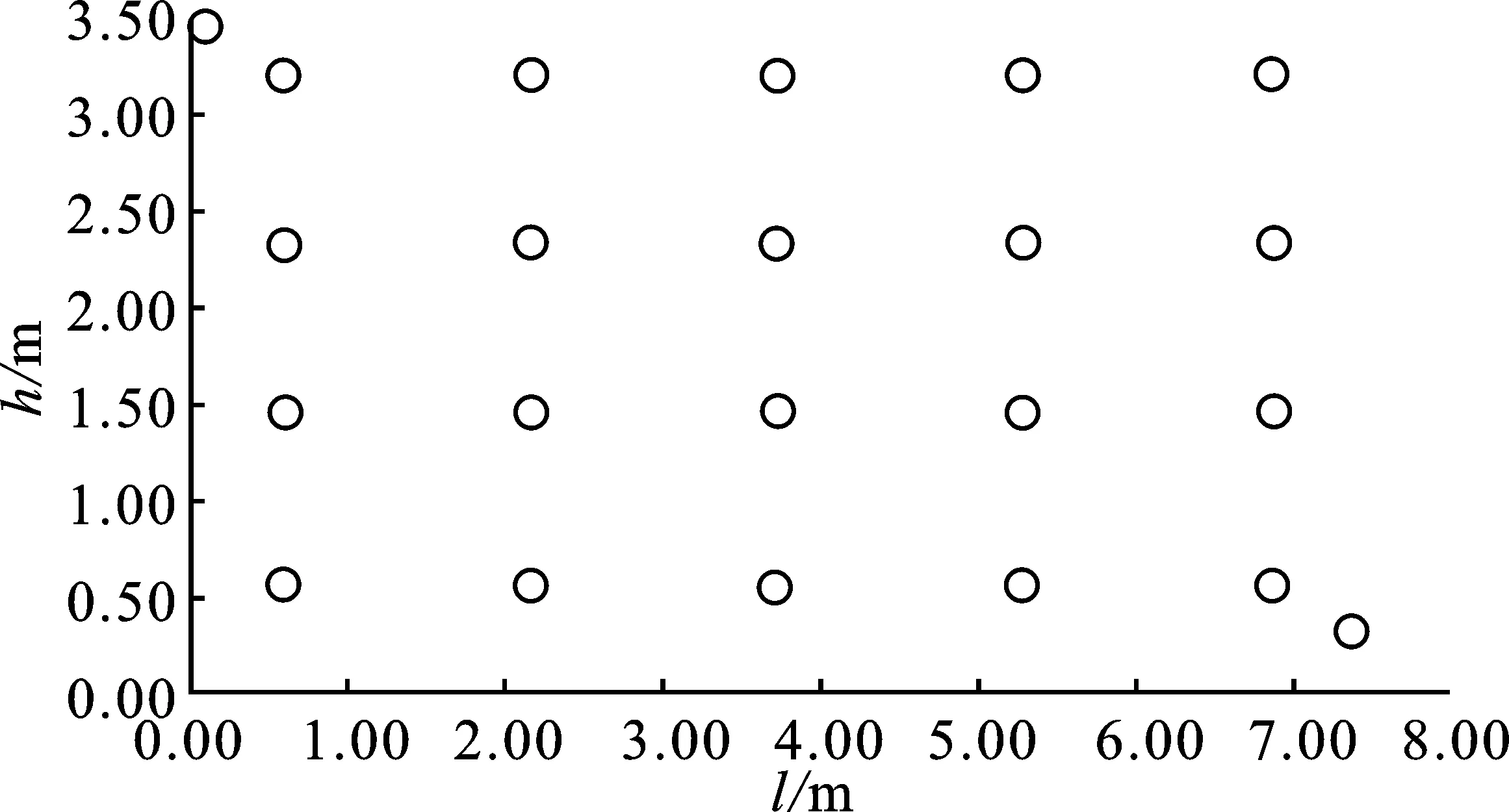
(a)

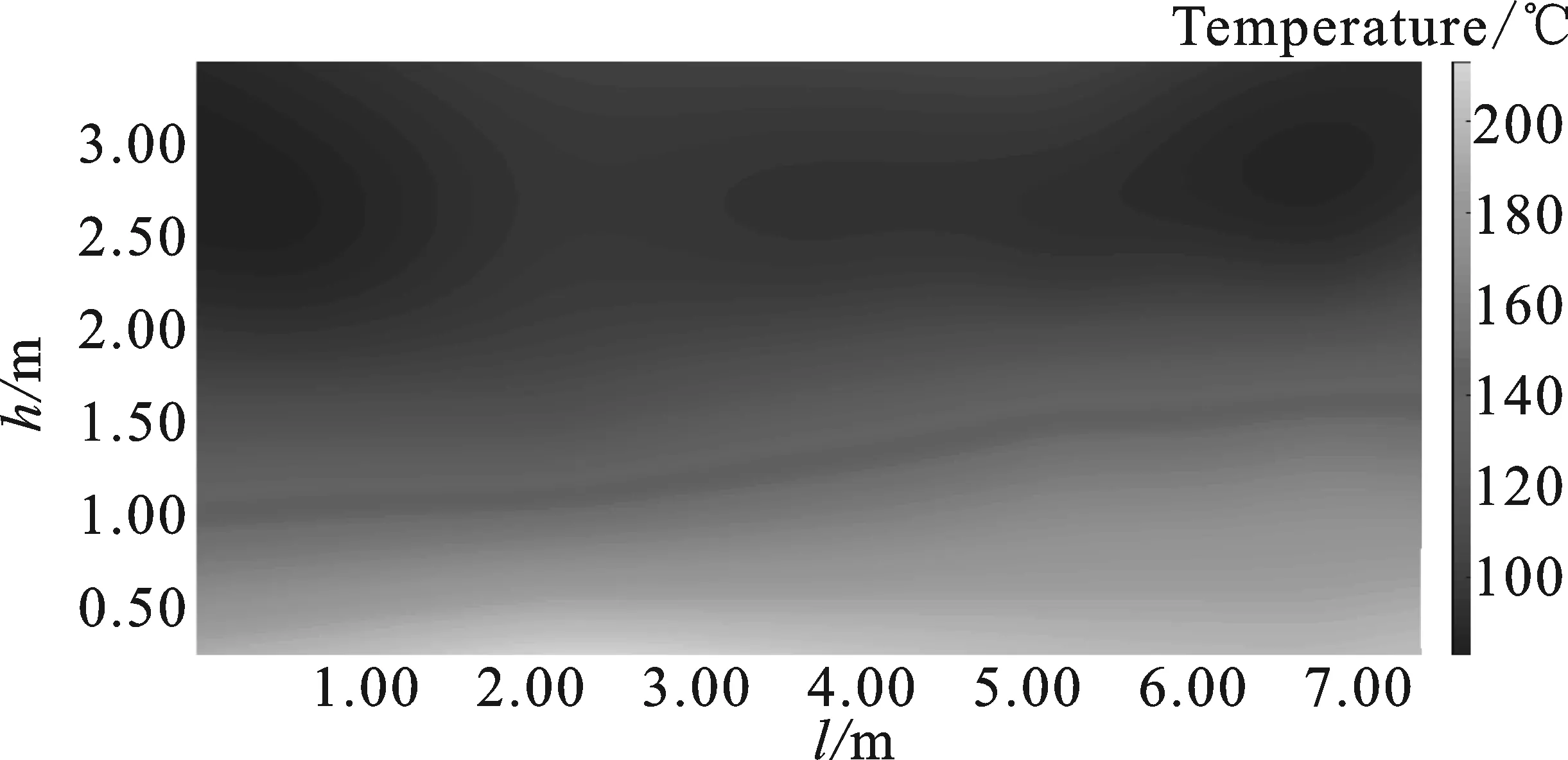
(b)图5 均匀布置传感器的位置及其重构的温度场(a)温度传感器均匀布置的位置 (b)采用RBF重构的温度场Figure 5. Location of evenly arranged sensors and theirreconstructed temperature field(a) Location of evenly arranged temperature sensors(b) Temperature field reconstructed by RBF method

图6(a)为采用GA优化后得到的22个温度传感器的位置。图中在UDD的左下方区域温度传感器布点较多，对应于理论温度场中，该区域的温度变化剧烈。其主要原因为气体向机壁运动，并在机壁附近形成气流漩涡，导致温度分布较为复杂。这里布置较多的传感器可以有效反映出这种趋势。坐标(7.39,0.33)处靠近气体入口位置，在这里的采样点可以有效反映气体的初始状态，在优化过程中得到点的位置。在UDD的高度为2 m以上，优化后的传感器布点主要采集到了3个部分，即对应于理论温度场中长度方向的左(0.00～2.00)、中(3.00～6.00)、右(6.00～7.40)3个部分。理论温度场中的温度变化趋势也主要体现在这3个部分，而采用较少的温度传感器就可以描述在这部分的温度形式。

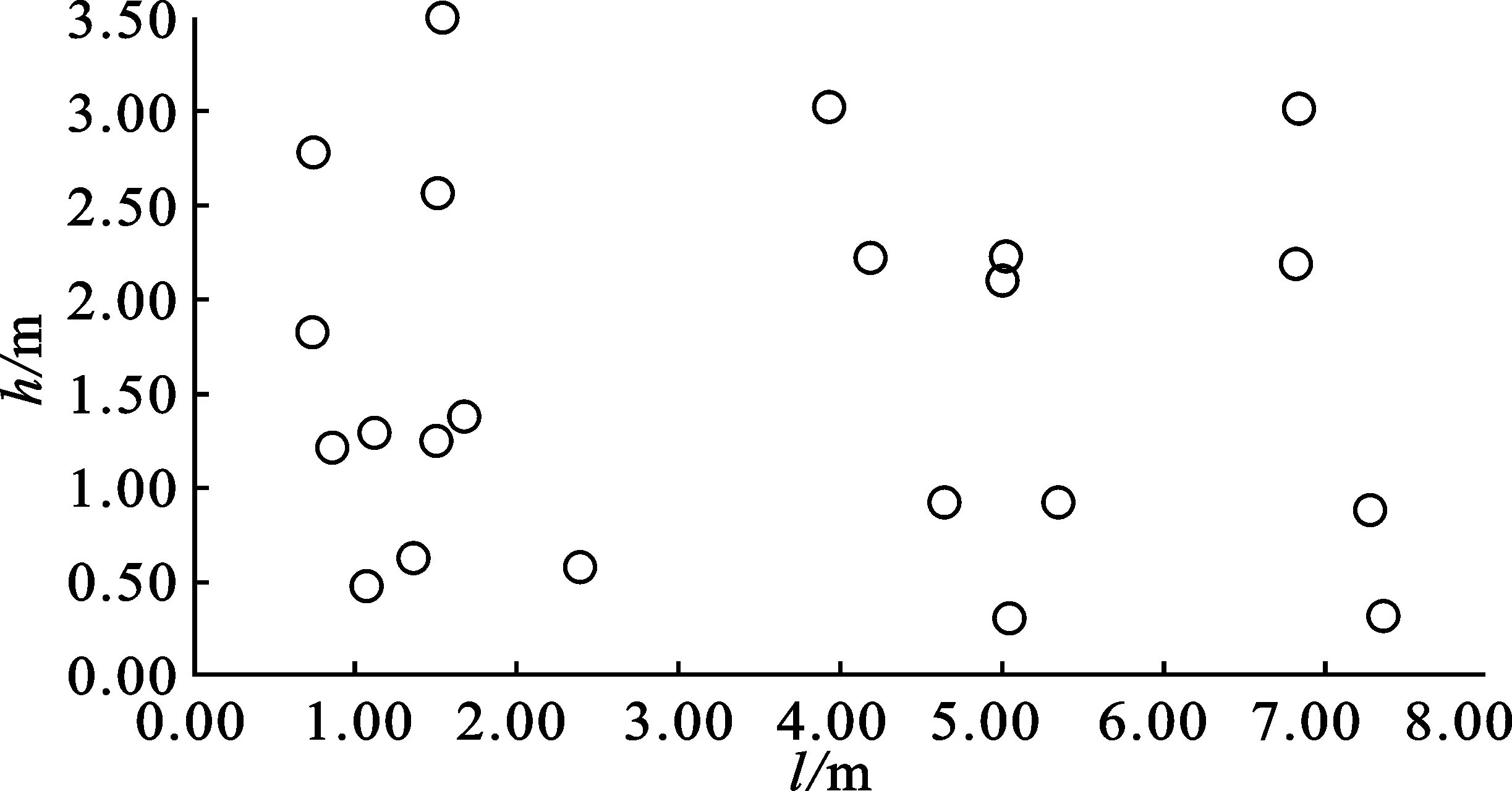
(a)

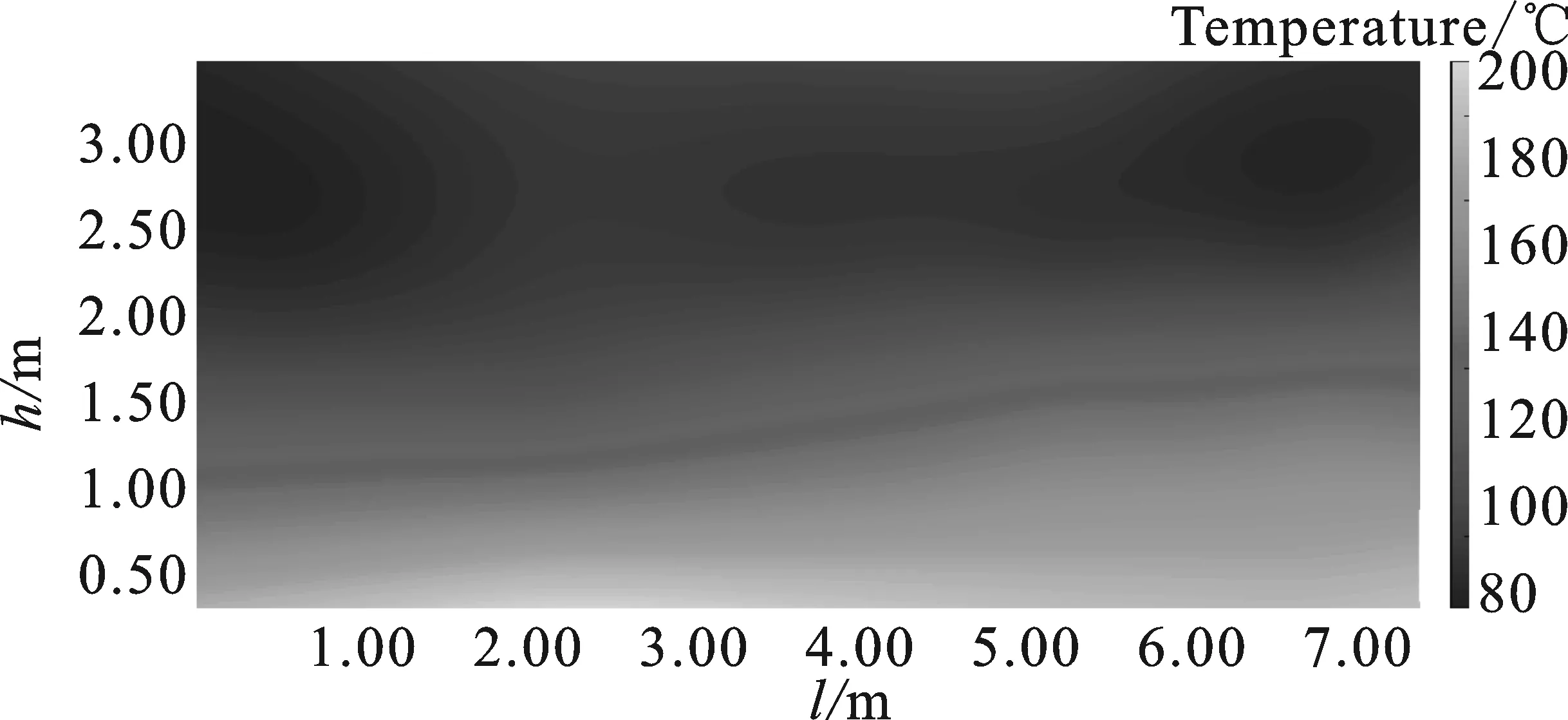
(b)图6 优化后传感器位置及其重构的温度(a)通过GA优化后的传感器位置 (b)采用RBF重构的温度场Figure 6. Optimized location and reconstructed temperature field (a)Optimized location of sensors by GA method (b)Temperature field reconstructed by RBF method

图 6(b)中，温度场与理论温度场较为吻合。在高度为1.5 m附近存在明显的温度场分界情况。因为高度为1.5 ～1.7 m为球团料层，是UDD主要的传热传质区域和阻力区域。气体入口附近的温度为200 ℃，向篦床行进方向的反方向递减，在长度0.0～1.6 m部分发生温度骤降，基本反映了理论温度场的变化特征。在高度方向1.7～2.5 m，长度方向为0～2 m组成的区域中，达到了局部极小值约为82 ℃，在理论温度场中也有所反映，比较好地反映了球团料层入口处的气体温度分布情况。

3.3 误差分析

图7(a)为采用RBF方法对均匀布置温度传感器下重构的温度场与理论温度场之间的误差云图，其最大误差为62.5 ℃，且位于(7.46,1.44)处。这部分是链篦机篦床出口位置，拟合温度场下存在局部的高温区，造成了这一部分误差较大。其平均绝对误差为12.2 ℃。与图7(b)相比，其高于40 ℃的误差区域较多，导致UDD中的温度场严重不平衡。

图7(b)为通过GA对本文提出的目标函数进行优化后，采用RBF方法重构温度场与理论温度场之间的误差云图。其中误差最大达到了59.3 ℃，但是这些误差较大点的数量很少，只分布在这些局部的低温区域及其附近。分析认为，这些误差极大值点的出现远超出温度场重构的要求。主要原因在于仿真得到的理论温度场存在一定的不连续性，而拟合或插值时则认为温度场是连续可导的，会对这些不连续区域做近似。如果取点不包含这些局部不连续的区域，会造成大误差产生。

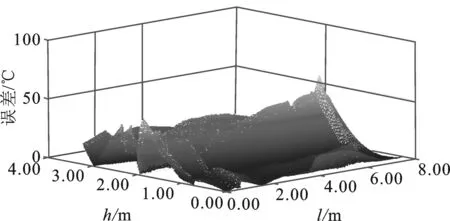
(a)

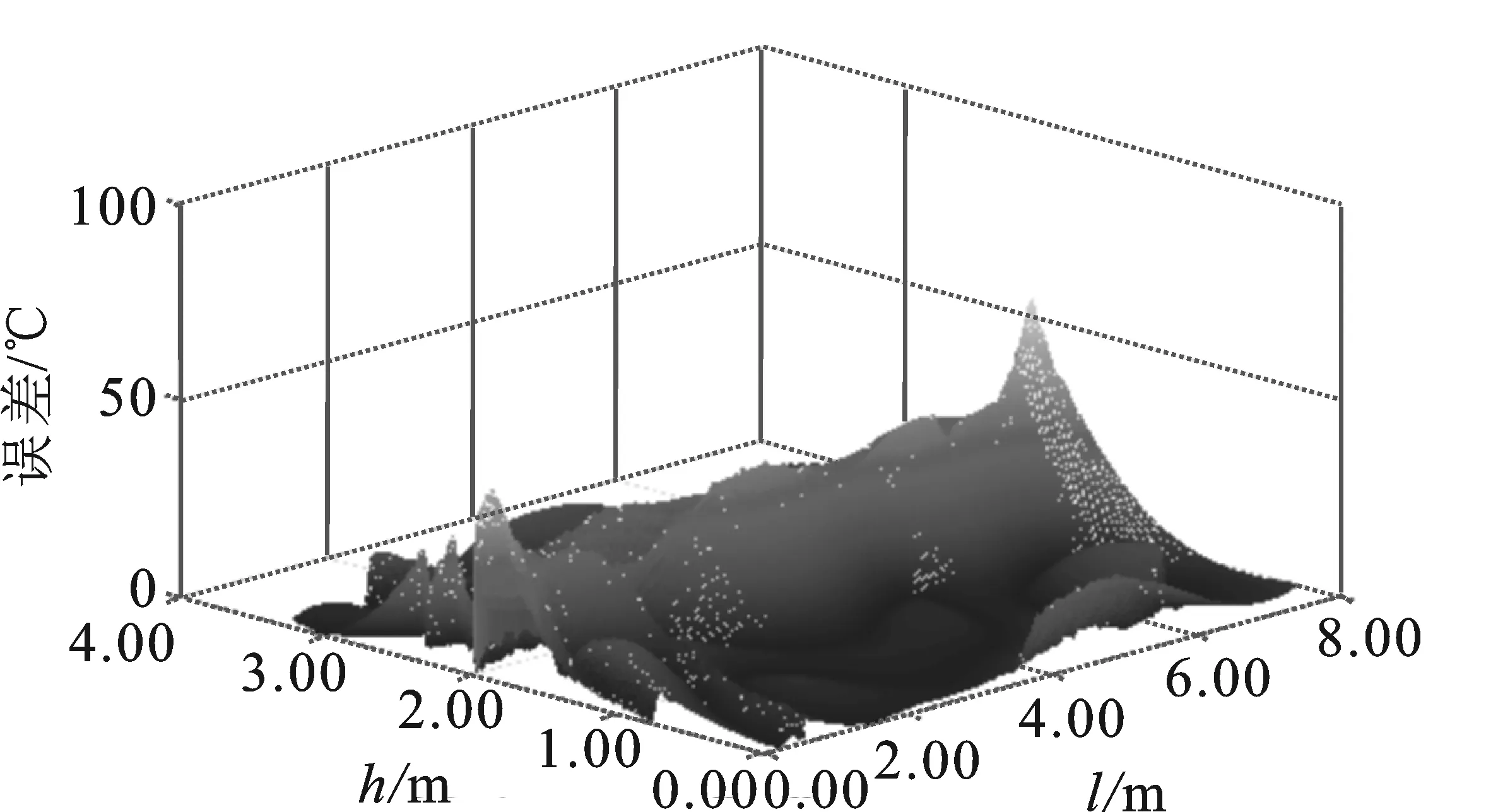
(b)图7 不同传感器布置方式重构温度场的误差 (a)传感器均匀布置后的温度场误差(b)传感器位置优化后的温度场误差Figure 7. Error of reconstructed temperature field with different location of sensors (a) Error of reconstructed temperature field with evenly arranged sensors (b)Error of reconstructed temperature field with optimized sensors location

采用模型命中率评估温度场的重构效果。模型命中率是一种用于判定拟合程度的数学方法，在数学上有一系列相近的定义和标准[22-23]，具体方程如下

(9)

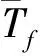
根据计算结果，当对传感器位置进行优化后，采用RBF重构的模型命中率为99.99%；均匀布置传感器下，采用RBF方法重构温度场，其模型命中率为99.88%。

4 结束语

本文针对链篦机工艺中的UDD温度场检测进行研究，得到以下结论：(1)在链篦机UDD中，温度传感器布置的数量与温度场重构精度并不是正相关。随着传感器布置数量的增加，温度场重构精度呈现出先升高后下降的规律。对传感器优化后的数量应选择22个，可以得到较高的精度。均匀布置传感器的情况下，温度传感器数量在16个以上时，重构所得到的温度场精度变化不大；(2)数值结果表明，在传感器数量相同的情况下，优化其布点位置的精度要高于未做优化的情况。在同为22个传感器时，优化后相比未做优化的平均绝对误差提高了30.90%；(3)计算结果显示，优化传感器后，采用RBF对温度场进行重构，温度场在其空间分布上与理论温度场差别不大，且模型命中率为99.99%。均匀布置传感器下，采用RBF方法重构温度场，其温度场与理论情况下差异较大，且模型命中率为99.88%。