基于统计滤波和稀疏度优化的印花配准算法
2021-09-02邓明舟雷建军
舒 军,邓明舟,雷建军,杨 莉
(1.湖北工业大学电气与电子工程学院,武汉 430068;2.湖北工业大学太阳能高效利用及储能运行控制湖北省重点实验室,武汉 430068;3.湖北第二师范学院计算机学院,武汉 430205)
近年来随着喷头技术和图像处理技术的不断发展,数码印花技术逐渐取代传统印花技术[1-2].其中OnePass数码印花技术采用多组喷头串排组合阵列,在扫描织物过程中,对布料实时喷墨上色,因此对图像配准的准确度和图像变形算法执行效率要求较高[3].
在数码印花图像的配准技术中,根据采集图像的不同可分为全局配准变形方法和局部配准变形[4]方法,全局配准变形方法是在织物扫描完成后分割出印花区域[如图1(a)所示],再进行配准和变形,该方法可通过少量控制点得到误差较低的变形图案,但采集图像需等待扫描结束,存在着滞后性,导致印花出现效率低、实时性差、漏印、错印等问题;局部配准变形方法是对扫描到的单帧图像[如图1(b)所示]进行实时配准与变形,优于全局配准变形方法,但采集图像无法分割出印花区域,因此背景噪声和变形区域增加,对算法的精度和效率要求较高,故本文针对局部配准方法所存在的问题展开讨论.

图1 不同的配准方法的输入图像Fig.1 Different registration methods for the input image
在图像配准[5]方面,由于工业现场的不稳定性,一般采用传统配准算法.文献[6]提出一种基于ORB[7]与RANSAC融合改进的图像配准方法,该方法在尺度和旋转配准性能方面有较大提升,但对边缘敏感性较高,应用到织物图案配准中,存在匹配近似点较多,误匹配率较高的问题.分析织物图像可以发现,织物在机械平台上一般呈柔性变形,即待匹配点与对应模板点仅存在局部位移.鉴于此,文献[8]采用FLANN匹配对大数据集和高维特征进行最近邻搜索算法,文献[9]在FLANN算法的匹配基础上加入RANSAC算法可有效滤除匹配误差点.文献[10]采用双向匹配法,采用多特征迭代的方式提高配准精度.文献[11]采用最近邻距离比值优化算法,将欧氏距离的偏移量作为特征进行配准.但是对于复杂度不同的织物图案,RANSAC和双向匹配法迭代次数差异性较大,存在算法实时性不稳定问题;而最近邻距离比值方法无法解决局部偏移量变化较大的问题,因此配准精度较差.
在图像变形方面,对于织物图案特性一般采用基于控制点的局部非刚性变形方法.该方法采用局部邻近结构拘束,若存在相关性较多的控制点将增加冗余计算,降低算法效率.
综上可知,织物图像匹配点的匹配度与点的欧式偏移距离相关性较大,变形控制点数量需要根据变形程度自动适应.本文基于FLANN匹配并结合统计滤波来剔除误差点;通过匹配点矩阵的稀疏度进行冗余优化,增加图像变形效率.
1 基于统计滤波的误差点剔除
分析织物图像可以发现,通过纹理、灰度等特征的匹配近似度较大,无法很好的剔除误差点.而织物在打印中主要存在局部形变,即匹配点在空间位移情况稳定.由此,本文采用匹配点的欧式距离差作为特征进行滤波.
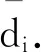
(1)
(2)
由设定的标准差倍数λ1,当点pi的距离di不在标准范围(μ-λ1×σ,μ+λ1×σ)内,则设定该点为误差点,进行剔除.得到滤波后的集合PR:
PR={μ-λ1×σ≤di≤μ+λ1×σ|pi∈P}.
(3)
上述算法时间复杂度为O(n×m),其中n为FLANN匹配后的所有匹配点,m为所有邻域Nbhd(pi)中总遍历点数的集合.因此可知邻域范围的选取直接影响着算法的使用效率.
假设邻域范围半径为r.分析可知,r增加可以提高滤波算法的精度,而r缩小可以增加算法速率.若每个不同邻域应Nbhd(pi)采用不同半径,即动态规划半径的范围,可提高该算法效率和鲁棒性.因此邻域的遍历方法为以pi为中心点出发做广度优先搜索(BFS),搜索顺序如图2所示.
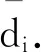

图2 BFS搜素顺序示意图Fig.2 BFS search sequence diagram

综上,邻域Nbhd(pi)的遍历步骤如下:
1)假设当前点为pi,从中心点出发;
2)基于BFS搜索下一点pj,判断pj是否超过最大搜索半径,若超过最大搜索边界,则终止搜索;

5)当前变化率k若小于近10次变化率中最小值的2倍时,遍历截至;否则判断变化率k若大于近10次变化率中最大值的2倍,则说明中心点pi为误差点,直接剔除;否则,更新近10次变化率最小值,继续执行步骤(2).
2 冗余优化
在织物图像变形算法中,一般将匹配点作为变形控制点.其中相关性较高的控制点对变形结果影响较小,并且降低变形算法效率.因此,本文将介绍一种自适应的冗余优化算法.
2.1 冗余点确定
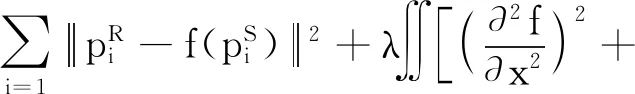
(4)
其中,点集之间的映射f为径向基函数的多重调和样条.为保持变形后曲面平滑性,避免噪声的影响,引入正则化参数λ使曲面不一定通过所有控制点,当局部区域的控制点较多时增加λ,从而减少平面的弯曲量.而针对织物图像特性,从平面角度看,邻域区域的弯曲量变化较少,因此当多个控制点存在邻域区域时,相关性较大,对公式(4)给出的能量函数影响较少.因此可将其视为冗余点.当冗余点过多时,会导致TPS算法时间复杂度过大,并对算法结果影响减少,所以需对冗余点滤除,提高算法效率、在统计滤波实验结果基础上进一步冗余优化,提出一种针对离散匹配点集的稀疏度度量方法,并通过稀疏度特征对PR做均值滤波,验证该方法的有效性.
2.2 匹配点的欧氏空间稀疏度
V=W×H,
(5)


已知由n个元素组成的矩阵X的稀疏度可由L1范数和L2范数的差异值来求得:
(6)
(7)

2.3 基于空间稀疏度的冗余优化
由(7)得到匹配点集PR中各点对应的稀疏度集合S.将稀疏度作为特征,当spi越趋向于1,视该点频率越高,为冗余点剔除;当spi越趋向于0,则视该点频率越低,为正确点保留.对稀疏度集合S做均值滤波,保留频率较低的点,得到优化后的点集PS.以此达到冗余优化的目的.
3 算法实验与分析
本文实验基于图像处理库OpenCV4.1.0和编程环境Visual Studio 2019,编程语言为C++,开发环境为CPU:Intel Core i7,GPU:GTX-1080,16GB内存,Windows 1064位,扫描仪采用的是PYTHON-400BW宽幅面线阵相机,有效扫描宽度为400 mm,像元密度为1 200 DPI,图像分辨率为1 200 DPI,实验样本图像分辨率为每幅19008×6000.织物选用蕾丝材质,其轻薄的材质在机械平台传动时更易发生局部形变.
下面首先分别对滤波优化和冗余优化算法实验,分析算法的可靠性;再对总算法进行对比实验分析精度和效率.
3.1 滤波优化实验分析
分析公式3中λ1对滤波效果的影响,实验设置不同参数λ1得到滤波后的匹配点集PR,通过人工查找误差点得到实验结果如图3所示.
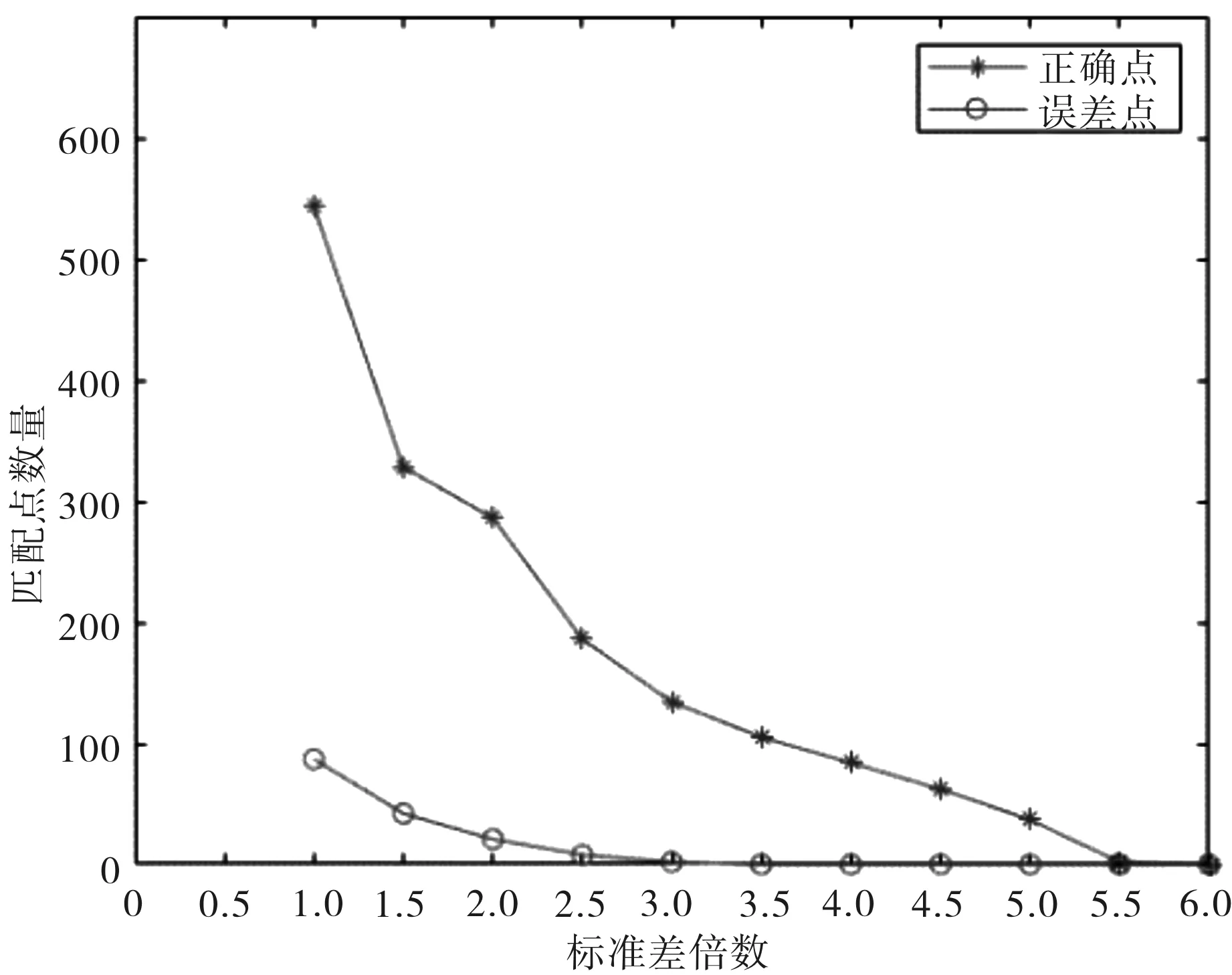
图3 λ1对统计滤波的影响Fig.3 the influence of λ1on statistical filtering
通过图3可见,当λ1过小误差点无法有效的滤除,因为标准差分量权值过低;但当λ1过大导致匹配点过少,影响图像变形效果.因此λ1的设置需考虑能有效滤除误差点的情况下,一定程度的保留匹配点作为控制点.针对本文应用设置λ1=3可达到理想效果.
为证明统计滤波在数码印花技术中匹配点优化的可靠性,通过FLANN匹配后的初步筛选与统计滤波后匹配点个数以及匹配点距离差进行对比,如图4和图5所示.
图4(a)可明显看出在FLANN匹配后的初步筛选结果中,存在大量由于匹配点距离差过大的误差点,最大误差点的距离差达到5 302个像素点,极大的影响匹配以及后续图像变形效果.经过标准差倍数λ1=3的统计滤波,如图4(b)所示,可以较好的滤除大量误差点,将匹配点的距离差控制在合理范围内.匹配效果如图5所示,通过该滤波算法后的匹配点中无误差点.

图4 匹配点距离差散点图Fig.4 Matching point distance difference scatter plot

图5 统计滤波匹配图Fig.5 Statistical filter matching graph
3.2 冗余优化实验分析
分析(7)中λ2对冗余滤波的影响,实验设置参数λ2将优化后的点集PS作为TPS控制点进行图像变形,通过采用均方误差统计参数和最大误差值作为实验精度评判标准,结果如图6所示.
均方误差统计参数是计算变形后的印花图案和参考图像的对应点间距离的平方和的均值[18],定义为
(8)
其中,f和g分别为变形后的参考图像上色点集f={fi|i=1,2,…,N}和参考图像的上色点g={gi|i=1,2,…,N}.
最大误差值是计算变形后的印花图案和参考图像的对应点间的最大距离差,即L∞范数,定义为
(9)
通过图6可知,当λ2取300~400时,最大误差和均方误差是最小的,则认为在此区间内λ2值做冗余优化最优.
为证明稀疏度度量的有效性,通过公式3得到的匹配点集合PR(图7(a))计算稀疏度,得到每一个点的稀疏度如图7(b),对匹配点的稀疏度作均值滤波得到滤波后的匹配点如图7(c),进一步计算均值滤波后点集的稀疏度如图7(d).

图6 λ2对统计滤波的影响Fig.6 the influence of λ2on statistical filtering

图7 基于稀疏度的均值滤波效果图Fig.7 Effect map of mean filtering based on sparsity
从图7(a)中可明显看出,由公式3得到的集合PR存在大量的冗余点,通过集合PR的稀疏度散点图7(b)可以发现,局部稀疏度较大的点为集合PR中的冗余点,但稀疏度存在一定的非线性因素.所以直接采用最大值滤波会将稀疏度较低区域的匹配点滤除,导致变形算法中控制点的完备性较差,最终导致变形偏差较大.采用均值滤波的方法,如图7(c),针对稀疏度均值滤波后可滤除大量稠密区域的匹配点,有效的将稠密特征区域稀疏化.如图7(c),均值滤波后点集的稀疏度相较于集合PR的稀疏度(图7(b))有明显的降低.
3.3 算法综合实验分析
在算法精度和效率要求方面,为满足系统实时性,每幅样本图像配准与变形在单线程下的计算时间不得超过15 s;精度方面图像变形后最大误差不得超过1 mm.
实验通过采集两次织物图像,一幅作为印花图像,另一幅作为参考图像,将两幅图像的SURF特征描述子的FLANN匹配点集数据作为输入.首先,采用邻域统计滤波对点集做粗提取,剔除误差点;然后,再通过计算各点稀疏度特征做均值滤波对匹配点优化;最后,将优化后的点集作为图像变形TPS算法的控制点.总算法流程图如图8所示.

图8 基于FLANN匹配的优化算法流程图Fig.8 Flow chart of optimization algorithm based on FLANN matching
表1针对不同匹配算法对图像变形精度的影响做实验验证分析,在FLANN算法的基础上分别加入RANSAC算法、双向匹配法、最近邻距离比值法、本文提出的统计滤波和进一步冗余优化的这五种配准优化方法对图像变形效果影响进行比对,图9为变形后的印花图案与参考图像分图叠加的结果,灰度较深的为变形后的重叠部分,灰度较浅的为变形误差部分,其中图9(a)为原印花图案与参考图像的叠加效果.
实验表明,RANSAC和最近邻距离比值法无法有效滤除配准误差点,导致变形后的图案无法覆盖参考图案,将导致输出错误的上色方案,如图9(b)和图9(d)所示;双向匹配法可以滤除一部分因匹配点距离差过高导致的误差点,但是无法完全剔除,导致变形依然存在较大误差,如图9(c);当加入匹配点距离差的统计滤波后可有效减少误差点,图像变形效果如图9(e),变形误差小于0.5 mm;在加入冗余优化后,如图9(f),图像变形效果基本无影响,证明冗余优化的点均为图像变形算法中的冗余控制点,最大变形误差小于1 mm,符合实验精度要求.

图9 不同匹配算法的图像变形效果图Fig.9 Image deformation renderings of different matching algorithms

表1 算法精度对比Tab.1 Algorithm accuracy comparison

表2 算法效率对比Tab.2 Algorithm efficiency comparison ms
在实验效率验证方面,表2针对不同配准算法分别在匹配和变形时间上进行实验分析.由于特征匹配前的特征点搜索效率不受匹配方法影响,因此总算法时间仅考虑图像匹配和变形时间.
实验表明,RANSAC和最近邻比值法虽在图像匹配算法效率上较优于本文算法,但由于匹配点较多,导致图像变形算法时间增加,导致总算法时间较长,并且由于较多的误差点导致变形存在较大误差,如图9(b)和图9(d);双向匹配法需要多次遍历配准点集,误差点滤除方面较优于前两者,但精度依然无法满足需求,如图9(c).因此RANSAC、最近邻距离比值法和双向匹配法在数码印花配准上局限性较大.在加入统计滤波后,虽然匹配效率微低于RANSAC和最近邻距离比值法,但匹配点更优,使得变形算法时间明显减少.在加入冗余优化后,变形控制点相较于优化前大幅度减少,可将总算法时间缩减至大约10 s,满足实验效率要求.
综上所示,通过本文算法与其他算法的误差点数量对比后发现,加入统计滤波可有效减少误差点,进一步加入冗余优化后对精度影响较小,表明优化算法对关键匹配点的完备性无明显影响.通过对比算法运行时间发现,加入冗余优化可以减少总算法时间.该算法能够较好地满足实验要求.
4 结论
针对局部印花图案配准变形方法中精度差、效率低的问题.本文提出首先一种基于统计滤波方法有效滤除匹配误差点,并通过广度优先搜索的方法对其优化效率;随后,提出一种稀疏度特征度量方法,基于该特征的冗余优化算法可减少变形控制点数量,提高算法效率.实验结果表明,该算法可有效滤除配准误差点,提高算法精度;并优化控制点集,提升算法效率.在数码印花领域应用,可增加印花效率,提高纺织业产量.
