线性代数中特征向量的一个应用

纪影丹， 谭 文

(广东工业大学 应用数学学院，广州510520)

1 引 言

线性代数是处理矩阵和向量空间的一个数学分支.线性代数可以用于工程学、计算机科学、数学、物理学、生物学、经济学和统计学中解释基本原理和简化计算.掌握线性代数的基本概念及应用技巧，为后续课程的学习和工作实践奠定基础[1].

特征值来源并应用于离散动力系统和连续动力系统.工程技术中的一些问题，如振动问题和稳定性问题，常可归结为一个方阵的特征值和特征向量的问题.特征值和特征向量在线性代数的学习中起着非常重要的作用，例如：线性方程组的基础解系可以通过求系数矩阵的特征值和特征向量得到；二次型的规范化可归结为对称矩阵的对角化问题，即验证是否有足够多的线性无关的特征向量；求方阵的幂及解微分方程组等问题.

在教学中要更多的融入科研工作，这样不仅能使教师更有效的传授知识，也能激发学生的学习积极性，并使学生对知识的理解更透彻.在教学过程中，应该让学生树立科研思维和发散思维，使其善于发现问题并能够利用所学知识灵活的解决问题，逐步掌握科研的方法和认识科研的一般过程.科研创新能力对学生综合实力的提高起着关键作用.

在为经管专业的学生讲授线性代数中一个利用特征值和特征向量求矩阵的例子时，有一个关于唯一性的疑问[2].在解决此问题后，又以此为切入点，提出猜测：是否可以利用以特征向量为列向量的矩阵刻画出所有与对角矩阵可交换的矩阵.本文第3部分证明了上述猜测是正确的.在科研过程中，经常会发现有意义的问题，然后就需要找到证明的办法.希望通过本文，能够使学生对如何在本科学习中开展科研工作有更清晰的理解.做为教师，也将继续努力寻找更加合适的方式把科研的思维和方法融入到教学中，提高学生的学习和创新能力.

2 问题的引入

定义1[1]设A，B是两个矩阵.如果存在可逆矩阵P，满足A=P-1AB，则称A和B是相似的.

定义2[1]设A是一个矩阵.如果存在λ和非零向量x，使得Ax=λx，则称λ为A的一个特征值，x为A的对应于特征值λ的特征向量.

引理1[1]不同特征值所对应的特征向量线性无关.

设A是一个n阶可对角化的方阵.设P=(p1，p2，…，pn)是一个n×n矩阵，其中列向量pi(1≤i≤n)为A的线性无关的特征向量.则P是可逆的.假设

Api=λipi， 1≤i≤n，

其中λi为A的特征值.令Λ=diag(λ1，λ2，…，λn)，则等式Λ=P-1AP和A=PΛP-1成立.

引理2[1]任意实对称矩阵都可对角化，且其属于不同特征值的特征向量正交.

例1设A是一个三阶矩阵，-1，1，0是A的特征值，且α1=(1，0，-1)T和α2=(1，0，1)T是A的分别属于特征值-1，1的特征向量.求矩阵A.

在教学过程中，学生在解例1时，会有疑问：k取不同的值，是否会得到相同的矩阵A？下面就一起来看一下.根据例1的解题过程，得到：对于任意的非零实数k1和k2，

P(k1)ΛP(k1)-1=A=P(k2)ΛP(k2)-1

(1)

成立.这样就得到，A的取值并不依赖于P(k)中k的选取.

另一方面，由(1)得到

P(k2)-1P(k1)Λ=ΛP(k2)-1P(k1)，

即，P(k2)-1P(k1)是一个和Λ可交换的矩阵.注意到，P(k1)和P(k2)都是以A(与Λ相似)的特征向量为列向量的矩阵.由此引出问题：是否所有与Λ可以交换的矩阵都可以写成P(k2)-1P(k1)这种形式？

3 主要结果

下面来解决上述问题，即：对于任意一个对角矩阵，用以特征向量为列向量的矩阵来刻画与其可交换的矩阵.

定理1设

是一个实对角n×n矩阵.则一个n×n矩阵U与Λ可交换当且仅当U=P-1Q，其中P和Q是满足下面条件的两个n×n矩阵，

(i)P可逆 ； (ii)存在一个n×n矩阵A，使得AP=PΛ，AQ=QΛ成立.

证先证明充分性.假设P，Q是两个n×n矩阵，满足条件(i)和(ii).令U=P-1Q.下面验证U与Λ可交换.利用AP=PΛ，以及P是一个可逆矩阵，得到A=PΛP-1.由于AQ=QΛ，得到Q的每个列向量都是A的特征向量，但这些特征向量不一定线性无关，因为Q不一定可逆.进一步，有

QΛ=AQ=PΛP-1Q.

于是

P-1QΛ=P-1PΛP-1Q=ΛP-1Q.

因为U=P-1Q，所以UΛ=ΛU.这样就得到U与对角矩阵Λ可交换.注意到，U是一个可逆矩阵当且仅当Q是一个可逆矩阵.

下面证明必要性，也就是证明每一个和Λ可交换的矩阵都可以表示成P-1Q这种形式，且P，Q满足条件(i)和(ii).设U是一个满足UΛ=ΛU的n×n矩阵.假设A是一个和Λ相似的矩阵.则A可以对角化.于是存在一个可逆矩阵P满足AP=PΛ，其实也就是把矩阵P的列向量按次序取为A的n个线性无关的特征向量，即(i)满足.因此，P-1AP=Λ，于是

UP-1AP=P-1APU，

令Q=PU，则U=P-1Q.这样就得到

QP-1AP=PUP-1AP=APU=AQ.

于是，QΛ=QP-1AP=AQ，即Q的列向量都是矩阵A的特征向量，(ii)满足.

注1 在上述定理的证明中出现的矩阵A不要求是对称矩阵，也不要求是可逆矩阵，后者主要是由Λ的对角线上有无非零元素决定.

特别地，如果上述定理中的对角矩阵满足对角线上相同的元素在相邻的位置，那么就得到下面的推论.

推论1设

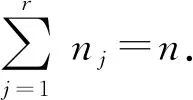
其中Uj是nj级矩阵(j=1，2，…，r)的准对角矩阵.

证设U=(uij)n×n是一个和Λ可交换的矩阵.根据定理1，存在一个n×n可逆矩阵P，两个n×n矩阵Q和A，使得等式U=P-1Q，AP=PΛ和AQ=QΛ成立.容易得到，P和Q的列向量都是属于矩阵A的特征向量.根据Λ的结构，对矩阵P和Q的列向量进行分组编号，得到

(q1，…，qi1，qi1+1，…，qi2，…，qir-1+1，…，qir)

=Q=PU

=(p1，…，pi1，pi1+1，…，pi2，…，pir-1+1，…，pir)U，

其中i1=n1，ij-ij-1=nj(j=2，…，r)，且ir=n.设1≤j≤r-1，则对任意的ij+1≤k≤ij+1，有

qk=u1kp1+…+ui1kpi1+ui1+1，kpi1+1+…+ui2，kpi2+…+uir，kpir.

注意到，对于j=1，2，…，r-1，

qij+1，…，qij+1(或者pij+1，…，pij+1)

是A的对应于特征值aj的(或者，线性无关的)特征向量.利用引理1，ut，k≠0当且仅当ij+1≤t≤ij+1，其中1≤t≤n.于是，qk=uij+1，kpij+1+…+uij+1，kpij+1.由此得到

是一个准对角矩阵，其中Uj是一个nj阶方阵，1≤j≤r.

注2 文献[3]给出上述推论的另外一种证明方法，大概思路为：先假设与已知对角矩阵交换的矩阵具有特定的分块形式，再利用分块矩阵乘法的相关性质，得到推论中的结果.对比两种证明方法，本文利用特征向量来构造矩阵的方法也许更让人耳目一新.

4 应 用

设A是一个可对角化的矩阵，且存在可逆矩阵P和对角矩阵Λ，使得P-1AP=Λ.设M是一个和Λ可交换的矩阵，即MΛ=ΛM.则

PMP-1·A=PMP-1·PΛP-1=PMΛP-1=PΛMP-1=PΛP-1·PMP-1=A·PMP-1，

得到PMP-1是一个和A交换的矩阵.令

S ={所有和A可交换的矩阵}， T ={所有和Λ可交换的矩阵}.

定义映射

Φ: S →T，NP-1NP，

则容易验证Φ是一个双射.所以利用与Λ可交换的矩阵可以表示出所有与A可交换的矩阵.也就是说，根据本文第3部分的主要结果，可以对与A可交换的矩阵给出完全刻画.

研究与特定矩阵可交换的矩阵是一个十分有意义的课题.例如：文献[4，5]证明，在一定条件下，与一个矩阵可以交换的矩阵一定可以表示为这个矩阵的多项式矩阵.可交换的矩阵会有一些特殊的性质.下面仅列举其中两个：若矩阵A，B可交换，则(i)A，B可以同时上三角化；(ii)(A+B)m满足矩阵的二项式定理.

注意到，若而当矩阵是对角矩阵的推广.所以自然的想法是，应用本文定理中的方法和思想，继续研究如何利用特征向量来刻画与若尔当矩阵可交换的矩阵.这是后续要开展的工作.

5 结 论

本文从一个引例出发，发现问题，并得到主要结果：对任意的一个对角矩阵，用以特征向量为列向量的两个矩阵刻画出了与其可交换的所有矩阵.在线性代数中，特征向量在矩阵的对角化过程中起着重要的作用.本文定理中的结果进一步验证了特征向量与对角矩阵之间确实存在着紧密的联系.以此为例，在以后线性代数的教学过程中，希望通过鼓励学生发现问题并积极主动的尝试解决问题，使学生自己发现新的结果.这不仅能使学生对所学的知识得到巩固，也能逐步激发和提升其科研探究能力.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.