“新工科”背景下《运筹学》创新思维培养的教学探索与实践——从一个课堂讨论案例谈起

赵金玲， 徐 尔， 孙玉华

(北京科技大学 数理学院，北京100083)

1 引 言

2017年2月18日，教育部在复旦大学召开了高等工程教育发展战略研讨会，讨论高校对新时期工程人才培养，探讨新工科的内涵特征、新工科建设与发展路径，形成了“复旦共识”，而后又相继产生了“天大行动”和“北京指南”，并发布了《关于开展新工科研究与实践的通知》和《关于推进新工科研究与实践项目的通知》，探索建立“新工科”建设的新理念、新标准、新模式、新方法、新技术、新文化.

运筹学作为一个应用性和实践性很强的数学分支，被广泛应用于经济管理、军事、工程技术、社会生产和生活各个领域，因而，运筹学在许多高校被设置为数学类和管理类本科生的必修课，也是一些理工类本科生的通识课和大量理工科研究生的重要选修课.从课程理念来看，运筹学讲求“运筹帷幄之中，决胜千里之外”，教学中在将优化思想根植于学生的思维中，建立不断寻优创优、追求优而更优的主动探索科学精神；从课程应用来看，运筹学与数学、管理学、经济学、工程技术等多学科深度交叉融合，优化技术亦在机器学习和数据科学中处于核心地位[1-2]，这些特点决定了在“新工科”的背景下，运筹学课程设计模式理念和创新思维培养导向对于理工科人才培养质量的提升起着关键性的作用.

早在2006年，胡发胜等介绍了山东大学数学与系统科学学院在运筹学教学中以“掌握理论、强化应用、突出能力”为课程培养目标的改革与探索，通过精选案例、实践教学、建模竞赛、改革考核体系等方式加强学生能力培养[3]；2019年，陈红兵等探讨了运筹学教学改革中的多元化教学模式和考核方式[4]；同年，陈家焱等具体讨论了以案例库建设为载体的运筹学课程教学改革[5].鉴于运筹学是一门应用极为广泛的交叉学科，在课程教学中注重理论与实践相结合，以应用性案例为思维启发点和实践着陆点目前已得到广泛认可，许多文献也进行了这方面的探索.

运筹学不仅是数学类和管理类高年级本科生的必修课，也是工科研究生的一门重要选修课，以北京科技大学为例，每年约有300名理工科硕博士研究生修读运筹学课程，其中95%以上是工科学生，而在“新工科”的背景下，对创新型工程人才的培养提出了更高的要求.近年来，《高等数学》等课程已形成了一系列关于创新意识培养的教学研究成果[6-8].《运筹学》作为一门应用广泛的课程，在模型建立和算法讲解的过程中，设计适当的教学情境，给学生充分的创造探索空间，让学生深度参与，既有助于学生增进对所学知识的理解，又有助于激发学生与课程思想内涵之间的共鸣.基于以上想法，本文主要探讨“新工科”背景下如何引导学生的运筹优化思维，提升学生的创新思维质量，以《运筹学》课程中教师引导的一次关于共轭梯度法的课堂讨论为例，尝试和探索通过问题驱动、激发头脑风暴来提升学生的优化创新意识和数学思维质量.案例中以学生为主体、由教师引导和激发学生创造力的创新性讨论模式更有利于学生在头脑中把相关知识“调动”起来，创造性地解决问题和进行理性分析.更为重要的是，这样让学生参与讨论、提出想法并分析解决问题的过程能够大大增强课程对于学生创新思维和科学精神的培养和塑造，强化了课程的育人效能.这一模式对于数学类和管理类《运筹学》教学以及其它类似交叉学科课程教学也有着较大的借鉴意义.

2 探索与实践

《运筹学》课堂教学改革，重在优化思维和创新意识的培养，可针对适当的内容，引导学生发现问题，层层递进分析解决问题，激发头脑风暴展开讨论，审视方法追求优而益优，从而达到将运筹优化思想根植于学生头脑和激发创新思维的目的.下面以一次关于共轭梯度法的课堂讨论为例来说明.

2.1 引导发现问题

首先引导学生发现以前所学方法的缺点和存在的问题.根据《运筹学》课程内容安排，在讲授共轭梯度法之前，已学习了求无约束优化问题minf(x)的最速下降法，其迭代步为：

x(k+1)=x(k)-λk∇f(x(k))，

其中λk为一维搜索步长.最速下降法采用当前迭代点xk处的负梯度方向-∇f(x(k))作为搜索方向，负梯度方向为该点处函数值下降最快的方向，故而称为“最速下降方向”.

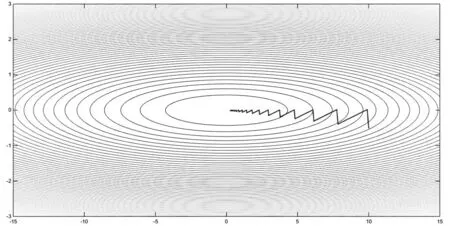
图1 最速下降法迭代中的锯齿现象

2.2 分析解决关键问题

不难发现，由于锯齿现象，最速下降法当迭代点接近极小点时，收敛速度显著变慢，这就引发了对于新的搜索方向的探索.那么怎样的搜索方向才更好呢？

定义1[9-10]设Q∈n×n是对称正定矩阵，若一组非零向量p(1)，p(2)，…，p(m)∈n满足：对∀i，j=1，…，m，i≠j，都有(p(i))TQp(j)=0成立，则称p(1)，p(2)，…，p(m)相互Q共轭，也称为Q正交.

从定义可见，Q共轭是通常意义下正交性的推广，当Q为单位阵，则为通常的正交.不难证明，Q共轭的一组向量必线性无关.

定理1[9-10]设Q∈n×n是对称正定矩阵，p(1)，p(2)，…，p(n)相互Q共轭，则从任意一点x(1)出发，依次以p(1)，p(2)，…，p(n)为搜索方向的下述算法

x(k+1)=x(k)+λkp(k)，

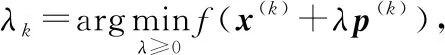
该定理中的算法实为共轭方向法，其中的精确一维搜索步长λk，对于定理中目标函数

是二次函数的情况，可通过公式

计算而得，与上节所讲最速下降法的步长计算类似.定理中所指出的共轭方向法经过至多n次迭代即可获得二次函数的极小点的性质，称为“二次终止性”，即，共轭方向法具有二次终止性.

至此，从算法收敛速度来看，共轭方向法具有更好的效率.那么，最为关键的就是，如何获得一组共轭方向呢？

2.3 激发头脑风暴，深入探讨解决方法

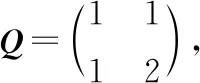
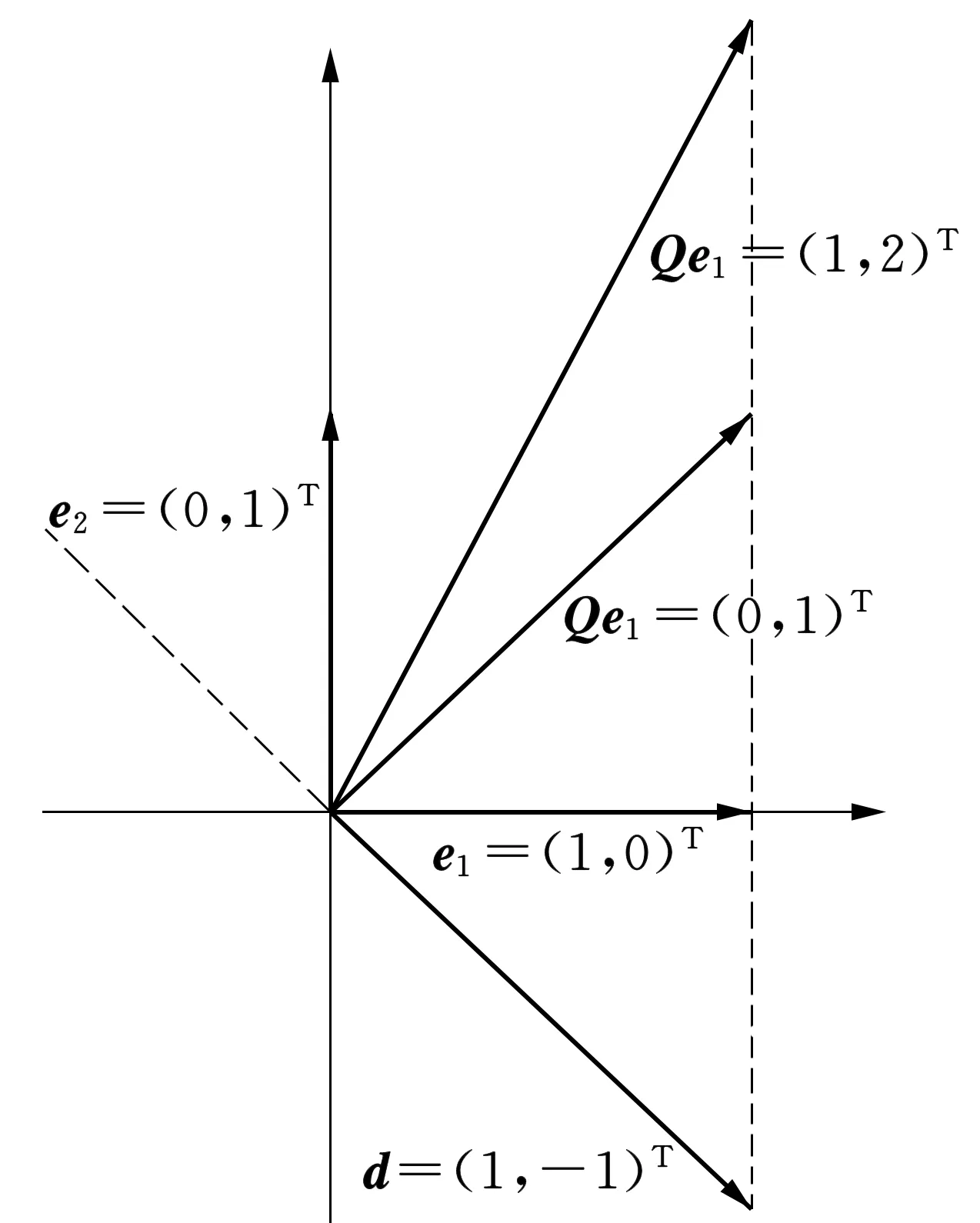
图2 正交与Q共轭

引导学生了解共轭方向在求解目标函数极小点中的重要性，并明确了共轭方向与对称正定矩阵Q联系密切之后，一个问题自然而然地产生了：该如何求得或生成一组共轭向量呢？展开课堂讨论，一名同学提出：是否可以映射到与Q有关的另一个空间来找方向？这为大家提供了一个思路.于是，已具备线性代数基础的同学们经过探讨得到了如下办法：由于矩阵Q对称正定，可将之分解为Q=MTM，利用Q共轭定义

(p(i))TMTMp(j)=(Mp(i))TMp(j)=0，

这说明p(i)和p(j)经线性变换后所得向量Mp(i)与Mp(j)正交，因此在n空间中可令

Mp(1)=e1，Mp(2)=e2， …，Mp(n)=en，

进而可解得

p(1)=M-1e1，p(2)=M-1e2， …，p(n)=M-1en，

e1=(1，0，…，0)T，e2=(0，1，…，0)T， …，en=(0，0，…，1)T，

又因Q对称正定，知M可逆.由定理1，依次采用这组方向进行精确一维搜索，即可经至多n次迭代收敛于

的最优解.进一步，有一些矩阵分析或计算方法基础的同学甚至明确指出，可以利用Cholesky分解[11]等方法来得到矩阵M，而且M是上三角阵，很方便计算p(1)，p(2)，…，p(n)，编写程序也很容易实现.

至此，老师很欣慰于学生们积极探索的态度和热烈讨论的氛围，大家能够基于已学知识，通过讨论自主发现一种生成共轭方向的方案，这无疑是非常值得鼓励的.同时，老师也在同步思考这一方法的可行性和计算效率.

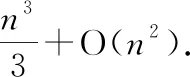
然后，老师提出第二个问题：这一方案的可拓展性如何？如果优化问题的目标函数不再是正定二次函数，没有明确的矩阵Q，还能否类似地得到搜索方向？这时，同学们发现，刚才所得到的求共轭方向p(1)，p(2)，…，p(n)的方法是基于矩阵Q的分解，不易推广到一般非线性函数的优化问题，因为一般非线性函数的Hessian矩阵不是常数矩阵.

2.4 审视方法优劣，寻求更快更优、拓展性更好的方法

老师所提出的两个问题，引导学生去思考和审视一种方法的计算效率和可拓展性，这正体现了运筹学教学中需传递给学生的不断优化算法、追求优而更优的思维方式和理念.有了上述准备，接下来水到渠成地引入利用迭代方式来生成Q共轭方向的共轭梯度法：

x(k+1)=x(k)+λkp(k)，

p(k)=-g(k)+βk-1p(k-1)(k>1)，p(1)=-g(1).

为简便，此处以g(k)记目标函数在xk处的梯度，即g(k)∶=∇f(x(k)))，λk为一维搜索步长.

共轭梯度法中，采用g(k)与上一次迭代中搜索方向p(k-1)的线性组合来构造共轭方向，运用了负梯度方向的同时，也充分利用了前次搜索方向的信息.当目标函数是正定二次函数

时，参数

可以证明，由该方法中的迭代p(k)=-g(k)+βk-1p(k-1)(k>1)，p(1)=-g(1)所产生的方向p(1)，p(2)，…，p(n)是Q共轭的，且精确一维搜索搜索步长

注意到上述βk-1的计算式中含有Q，如欲推广到目标函数更一般的情形，需公式中不再含有Q.由于

g(k)=Qx(k)+b，g(k-1)=Qx(k-1)+b，

故而，有

g(k)-g(k-1)=Q(x(k)-x(k-1))=λk-1Qp(k-1)，

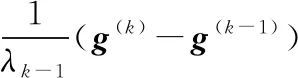
这便是著名的Hestenes-Stiefel公式(Hestenes et al.，1952).这样就将共轭梯度法推广到了目标函数是一般非线性函数的情形.当然，此时步长λk应采用一维搜索技术来计算.

注意到采用精确一维搜索时有(g(k))Tp(k-1)=0，则上式可化为

该公式被称为共轭下降公式(Fletcher，1987).

若对分子和分母进行变化，则不同的组合可演变出不同的βk-1的选取方式，对应着不同的非线性共轭梯度法，著名的βk-1的选取方法有如下四种[4]：

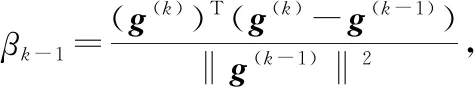
分别称为Fletcher-Reeves公式、Polak-Ribiére-Polyak公式、Hestenes-Stiefel公式(前面已提到过)和Dai-Yuan公式.此外，若沿用共轭下降公式中的分母，还可以得到

即Liu-Storey公式.

以上公式的推导并不困难，事实上，由精确一维搜索可知，(g(k))Tp(k-1)=0，又注意到

p(k)=-g(k)+βk-1p(k-1)，

不难知道

-(p(k))Tg(k)=(g(k))Tg(k)=‖g(k)‖2，

此外，还可以证明得到(g(k))Tg(k-1)=0，从而，以Hestenes-Stiefel公式为基础，对分子和分母进行不同的演变，即可得到上述公式.

此刻，学生很自然会想到一个问题：这么多公式都是为了计算共轭梯度法中的βk-1，这样来回转化有什么意义呢？其实不难发现，当目标函数是二次函数的时候，上述公式是等价的，但它们对于一般的非线性目标函数并不互相等价，从而对应的是不同的共轭梯度法.而且，在算法执行的过程中会受到计算中误差累积的影响，故而往往存在“等价不等效”的现象.上个世纪后半叶，近50年的时间里，人们对于各种共轭梯度法收敛性和收敛速度的讨论可谓是一场思维盛宴，精彩纷呈，建议学生拓展阅读文献[10，12].

至此已看出，共轭梯度法的拓展性优于最初学生讨论所得的方法，而且，由于共轭方向是由迭代点处负梯度方向与前一次搜索方向的线性组合，连同βk-1的计算，其中只需向量乘法与加法运算，大大降低了计算复杂度.

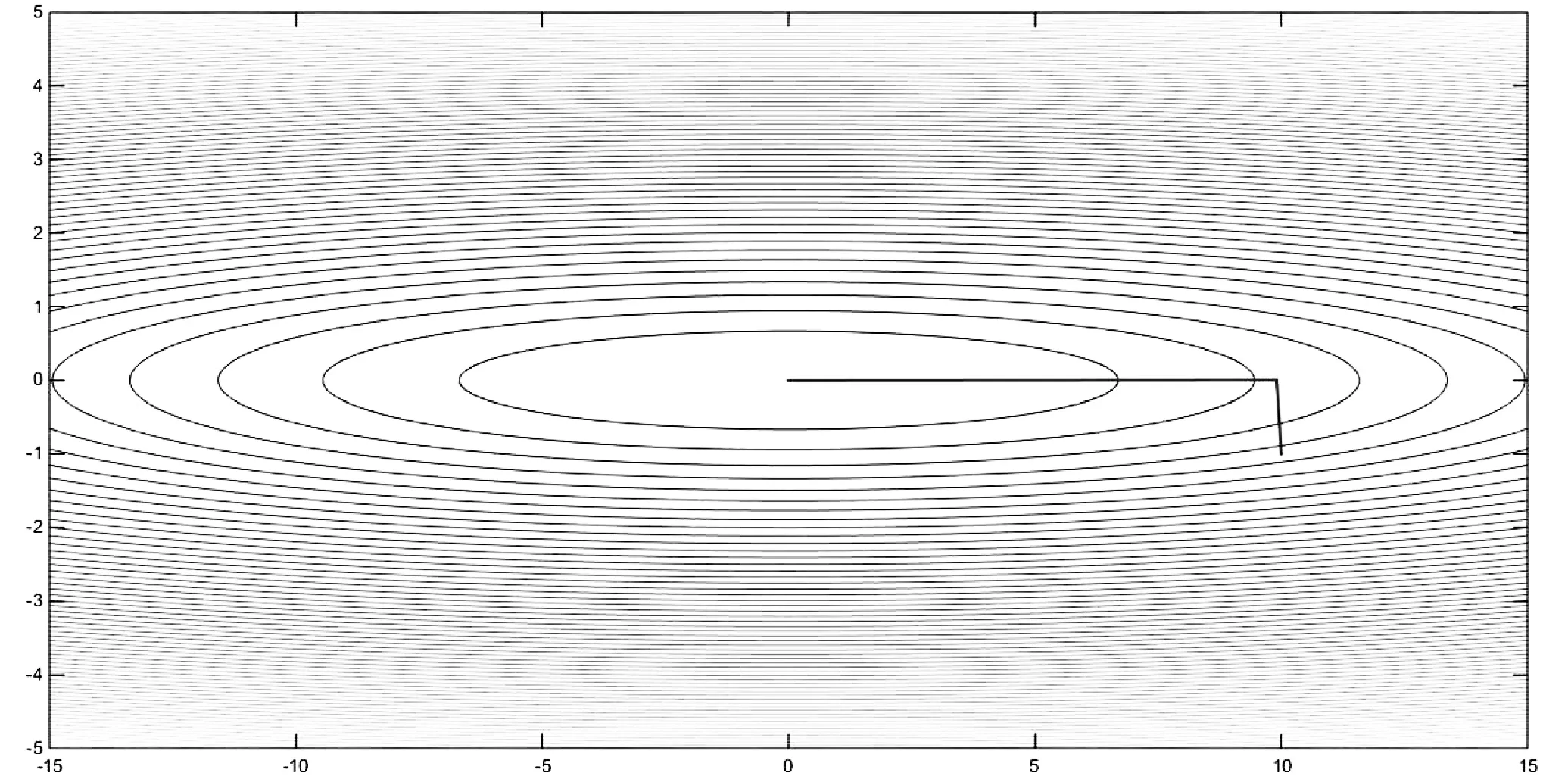
图3 共轭梯度法迭代过程

3 教学效果

图4 教学效果评价

该课堂讨论案例中，教师针对学生所提出的有价值的问题、想法和关切点，激发头脑风暴，引导大家讨论解决问题，并得到了一种新的方法，进一步带领学生进行算法优劣的比较，最后因势利导地回归授课内容中的共轭梯度迭代方法.虽然学生所得到的方法具有局限性，但学会审视方法的优劣也非常重要，这样以学生为主体的学习讨论可让学生对共轭梯度法理解更深刻，讨论过程也有利于学生优化意识和创新思维的培养.

在课程评价中，学生对于这样的讨论形式也是颇为肯定，表示“更能激发求知欲”，“对科研思路很有帮助”，“不仅有了科学的规划手段，还形成了合理的思维方式”，课程满意度达到99%，其余1%为基本满意，不满意为0.还有学生建议增加关于应用案例、建模、算法实现等的讨论.在此基础上，作者主讲的理工类研究生《运筹学》课程获北京科技大学第九届“研究生教育奖”.

4 结 论

本文结合《运筹学》教学中的一个课堂讨论案例进行了关于如何培养学生创新思维和激发寻优创优意识的探析.案例中，学生通过参与讨论带着兴趣主动地完成了一次运筹方法构造的训练，对于其提升数学思维质量和创造性思维大有助益.运筹学旨在培养学生建立系统思维，掌握定性与定量分析相结合的数学建模方法，运用优化技术手段求解，进而作出决策和指导实践的能力.正所谓“运筹帷幄之中，决胜千里之外”，运筹学教学目标不仅是让学生掌握建模方法和求解算法，而是在教学理念中将引导学生的优化思想和追求优而更优的思维方式贯穿于始终，从知识层面上升到思想层面，激发创造性思维和自主探索新方法和新技术的科学创新潜质；与此同时，也把运筹学的思维方式作为载体，将不断追求卓越和超越自我的价值理念深扎学生心中，达到润物无声的课程思政育人效果.本文是为更好地达成这一教学目标的课堂实践探索和教学思考.

此外，有成效的课堂讨论对于教师而言也是教学相长的实际体验，并且对教师提出了更高的要求，需要对线性代数、矩阵分解理论和数值计算等均有相当的知识储备，才能予以有针对性的引导和反馈.故而，欲将学生自主创新讨论融入课堂，高素质的运筹学课程教学团队建设也势在必行，可定期组织教学研讨，从而提高整个团队的育人质量.

致谢作者对参考文献给予本文的重要启示以及审稿专家对本文修改所提出的宝贵意见和建议致以由衷的感谢.