岩质边坡开挖对近接杆塔基础影响分析

刘燕平，周文俊，章李刚，王金昌

（1.浙江华云电力工程设计咨询有限公司，浙江 杭州 310014；2.浙江大学建筑工程学院，浙江 杭州 310058）

0 引 言

电力是整个国民经济中重要的支撑，基础作为杆塔和地基之间的连接构件，是输电线路中重要的组成部分，其稳定性是输电线路正常、可靠工作的前提，也关系到整体输电网络的安全。杆塔以线状分布于不同区域，主要包括平原区和山岭区，而平原区以表面平整的分布软土地层为主，而山岭区以倾斜的表面含有坡积层不同风化的岩层为主。

在土地资源紧缺以及环保要求提高的现实状况下，杆塔建成后不可避免的出现邻近各种工程建设，譬如开挖、堆填等。新建结构物邻近既有结构物施工，并可能对既有结构物产生不利影响的工程称为近接工程，有关近接工程的施工称为近接施工[1]。针对周边近接新建工程施工对杆塔基础的影响研究尚不多见。岩土体开挖堆卸载工程施工会扰动周边地层，引起土体应力场变化，影响杆塔基础，从而对杆塔结构安全和正常使用产生影响，情况严重的甚至会导致结构过早的破坏和失效，影响电网的安全使用。本文以山区杆塔基础为背景，研究岩质边坡开挖对杆塔基础的影响。

1 数值模型建立

1.1 计算模型

计算以典型边坡横断面为例，如图1所示。整体尺寸为宽210 m、高125 m，分步开挖，每次开挖深度8 m，分5次开挖，边坡底宽62 m、顶宽112 m。以Plaxis有限元软件为计算平台，建立数值分析模型，采用高次插值函数的平面三角形 15节点单元进行网格部分，如图2所示。模型共1 153个单元，9 738个节点。计算模型采用平面应变，在模型左、右侧和底部边界均施加与之相垂直的约束条件。

图1 边坡断面的计算示意图Fig.1 Calculation diagram of slope section

图2 有限元网格模型图Fig.2 Finite element mesh model diagram

1.2 本构模型及参数

Plaxis有限元软件内嵌多种经典及高级岩土体本构模型，能模拟复杂岩土结构和施工过程，在岩土工程研究领域得到广泛应用。计算采用霍克布朗（Hoek-Brown）经验准则对边坡进行计算分析。该经验准则采用最大主应力σ1和最小主应力σ3的关系式来描述岩体临界受力状态[2]，见式（1）所示：

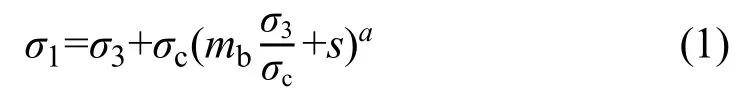
式中：mb为完整岩石参数mi的折减；s，a为岩块的材料参数，由地质强度指数GSI和扰动因子D共同确定。

式（1）中的s和a可由式（2）～（4）来确定：

式中：mi可根据岩石的类型进行确定。

岩石的单轴抗压强度σc可根据完整岩石单轴抗压强度σci确定：

由式（1）～（4）可以看出，岩石的Hoek-Brown强度可由mi、GSI、D和σci这4个参数进行确定，可以通过查表的方法确定准则中所需的参数[3]。为简化起见，本文选取常见岩体砾岩作为代表，采用单一土层进行计算分析。砾岩的基本参数如下：重度r=25.4 kN/m3，弹性模量Erm=3 700 MPa，泊松比μ=0.15，单轴抗压强度σci=308 MPa，完整岩石参数mi=19，地质强度指标GSI=55。杆塔基础以ZF1660灌注桩单桩进行分析，桩长32 m，桩径1 m，C30混凝土材料，采用嵌入式梁单元进行模拟。

2 岩体参数敏感性分析

霍克布朗模型虽给出了确定岩体整体抗剪强度的方法，但采用该方法确定的岩石参数存在一定的主观性，尤其是岩体参数GSI是一个范围值，且不同地质人员对相同的岩石所得出的GSI范围也会出现误差，需要定量分析这些差异对边坡稳定性计算产生的影响。此外模型中的其他3个参数单轴抗压强度σci、完整岩石参数mi以及扰动因子D对稳定性也有影响。完整岩石参数mi为常量，由岩石的具体种类决定[4]。本文选取砾岩进行研究，对模型的GSI、σci以及D进行敏感性分析，采用计算得到的安全系数Fs作为指标，通过各曲线的变化趋势判断各参数对边坡开挖稳定性的影响。

根据霍克布朗经验准则，扰动因子D取值范围0.7～1，GSI取值范围10～80。扰动因子D反应的是爆破效果，是岩体在爆破开挖过程中所受的扰动情形，其值越小越好，但开挖卸载不可避免会改变原有岩体的应力分布。为简化分析过程，先将mi与D设为定值，D取建议值0.7[5]，即边坡开挖破坏程度较低，调整参数GSI与σci进行参数敏感性分析，然后再对扰动因子D进行敏感性分析。

2.1 GSI与σci敏感性分析

在霍克布朗模型中，参数GSI是描述岩体结构与结构面表面特征的指标，图3为砾岩参数敏感性曲线，可以看出GSI越大边坡稳定性越高。Fs与GSI的变化规律可分为两个部分：当GSI为10～50时，Fs-GSI曲线表现为线性相关，且Fs增长趋势较为平缓；GSI为 50～90时，Fs-GSI曲线表现为指数关系，安全系数Fs随GSI的增加而急剧增加。σci为岩体的单轴抗压强度，在图4的Fs-σci曲线中可以发现，安全系数随σci近似线性增大。但当GSI=10，σci＜40 MPa后，由于参数整体取值过小导致模型计算失败，出现部分曲线数据缺失。

图3 Fs-GSI曲线Fig.3 Fs-GSI curve

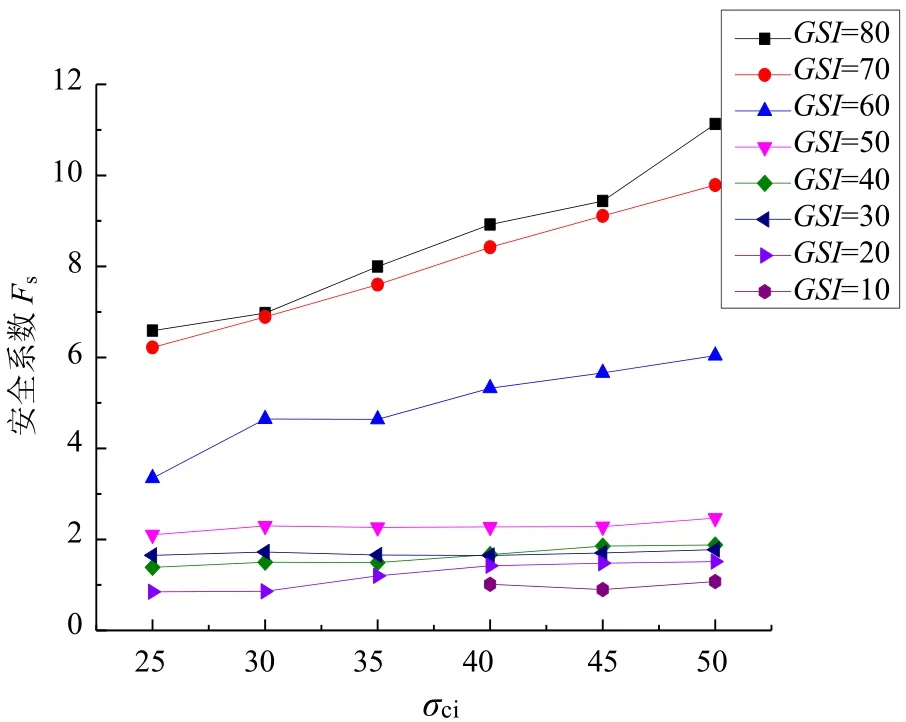
图4 Fs-σci曲线Fig.4 Fs-σci curve

2.2 扰动因子D敏感性分析

扰动因子D反映了边坡开挖对原有岩体的扰动程度，扰动越小D值越小，边坡安全系数Fs越高。图5为不同扰动因子下不同的抗压强度GSI和σci对边坡安全系数Fs的影响，从Fs-D曲线的整体变化趋势可以看出，其与Fs-σci曲线一样呈线性相关，Fs随D的增加而减小。图中GSI=10曲线部分数据缺失原因同2.1节。

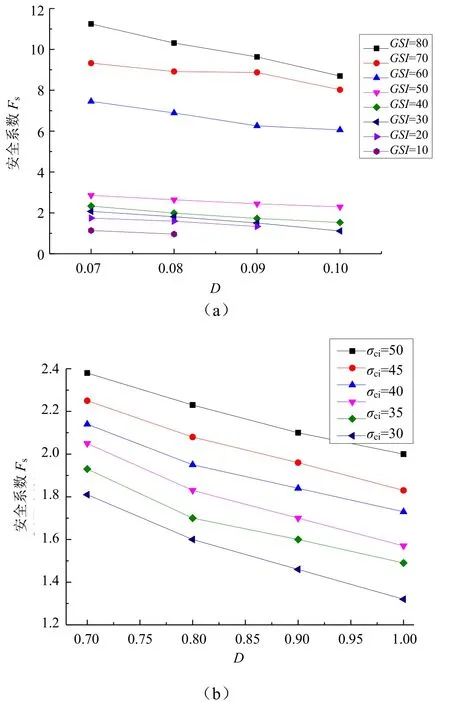
图5 Fs-D曲线Fig.5 Fs-D curve

上述参数各自具有不同的物理意义，为直观判断各参数对边坡稳定性影响的大小，采用相对误差的方法对数据进行处理。假设系统特性L是由n个因素a={a1，a2,…,an}共同决定，系统模型表述为L=f{a1，a2,…,an}，系统特性为L*。各因素的变动都在各自变动范围内变化，某因数引起系统特性L*偏离基准状态L为ΔL，敏感性δk(ak)具体描述为：δk(ak)=(|△L|/L)/(|△a|/ak)。GSI、σci和D这3个变量分析结果如图6所示，通过求解曲线交点处斜率来判断各参数的敏感性变化。可以发现图中各曲线斜率kGSI＞kD＞kσci，因此判断敏感性GSI＞D＞σci，安全系数Fs对地质参数GSI最为敏感。

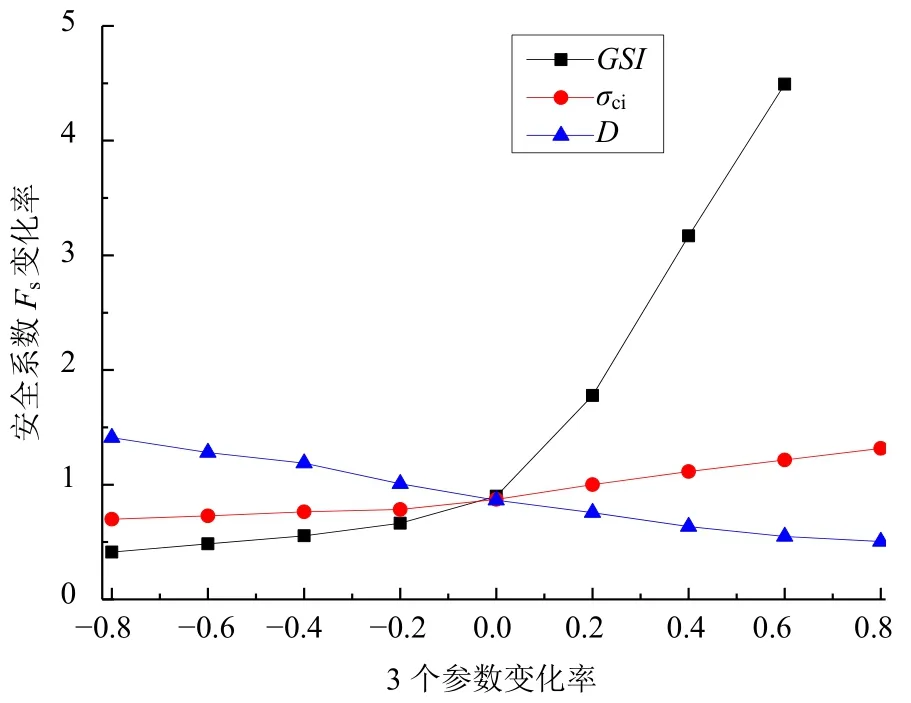
图6 各参数变化规律Fig.6 Variation of each parameter

3 开挖对杆塔基础变形及影响区划分

3.1 变形特性分析

开挖过程中不同开挖深度下的位移等值线分布规律总体相似，其中第一次开挖和第五次开挖位移等值线分布如图7所示。随着开挖深度的增加，最大位移逐步增加，并向远场传递。最大位移等值线由开挖的底部向右下方逐步减小，对于不同位置处的杆塔基础位于不同的位移等值线影响范围内，受边坡开挖的影响也有差异。因此在实际工程应用中，应该结合杆塔与坡顶的相对位置划分合理的影响范围，避免杆塔基础产生过大变形。

图7 不同开挖工况总位移分布图Fig.7 Total displacement distribution of different excavation conditions

3.2 位移影响区划分

提取不同开挖工况下坡底及距离坡顶不同位置处（5～30 m，间隔5 m）的杆塔基础（0～30 m，间隔5 m）最大位移，见表1所示。由表可知，边坡开挖产生的最大位移在坡底，其最大位移远大于位于坡顶不同距离的杆塔基础的位移；同一工况下距离坡顶水平距离越远，开挖产生的位移越小。

表1 不同位置的最大位移Table 1 Maximum displacement at different positions

根据上述位移影响分析，参考《架空输电线路杆塔基础设计规范》[6]第 9.6.3条中规定的不同地基土类别下单桩水平位移，以±10 mm最大位移为控制值，±5 mm最大位移为警戒值，绘制不同工况下杆塔基础最大位移等值线分布图如图8所示。定义最大位移小于5 mm的为弱影响区；最大位移大于5 mm且小于10 mm的为中影响区，该范围内的杆塔基础虽然位移尚未达到控制值，但应引起高度重视，进行合理的监测，采取有效的防范措施，并制定应急处理方案，防止基础变形继续增加；最大位移大于 10 mm的为强影响区，其位移超过控制值，在基坑施工过程中必须采取相应措施对杆塔基础进行保护，使位移满足控制要求。

图8 不同开挖工况下杆塔基础最大水平位移等值线分布图Fig.8 Isoline of maximum lateral displacement of tower foundation under different excavation conditions

4 结 论

本文基于Plaxis有限元软件建立了典型岩质边坡开挖数值模型，得出以下结论：

（1）对霍克布朗准则进行敏感性分析，从计算结果得出参数敏感性为GSI＞D＞σci。

（2）岩质边坡开挖时最大位移位于开挖底面处，随着开挖深度的增加，最大位移逐步增加，并向远场传递。

（3）边坡开挖将引起坑外近接杆塔基础产生变形，根据开挖变形特性和杆塔基础的控制标准，可将开挖变形影响区划分为弱影响区、中影响区和强影响区。

此外，边坡开挖对杆塔基础的影响不仅与开挖深度、坡顶和塔基的水平距离有关，还与塔基的桩长等相关，日后还应继续进行深入研究。同时，杆塔基础的存在也会改变岩土体刚度，影响位移场分布特点，因此对于边坡开挖对既有杆塔基础的影响，也应结合具体情况单独分析，判断对结构的扰动程度，从而进行针对性保护。