平滑新能源波动的混合储能优化配置

金鑫，王凯

(1.青岛大学 电气工程学院，山东 青岛 266071；2.国网山东省电力公司平原县供电公司，山东 德州 253000)

减少碳排放已经成为我国未来发展的重要目标，到2030年，我国将完成碳达峰，到2060年我国将完成碳中和[1-2]。在国家节能减排政策的支持下，越来越多的新能源发电涌入电力系统中，由于新能源发电存在的波动性与不确定性，导致电力系统复杂程度节节攀升[3-4]。

近些年，储能系统成为解决新能源发电波动性与不确定性的重要途径[5-7]。储能参与新能源并网主要应用于电源侧，利用储能的快速响应调节新能源发电的出力，以满足并网要求。文献[8]运用锂离子电池和新能源发电功率共同输出，从而降低新能源发电功率的波动性。文献[9]运用飞轮储能平滑新能源出力的波动性，通过模糊控制对系统输出功率进行限制。以上文献均为单一储能平滑新能源发电出力的波动性，并未考虑新能源发电出力的频率响应特性。为使新能源发电出力平滑更加优化，混合储能系统被越来越多地应用于新能源发电出力的平滑。文献[10]通过超级电容和电池储能相结合，共同应用于新能源发电出力的波动平滑。文献[11]通过飞轮储能平滑新能源发电出力的高频功率波动和部分低频功率，通过蓄电池平滑剩余部分的波动，从而保持电压平衡。文献[12]通过蓄电池和超级电容器储能平滑新能源发电出力的波动性，考虑了新能源发电出力的双评价指标。文献[13]采用锂电池和超级电容相结合的储能系统平滑新能源出力的波动性，通过小波变换平滑新能源发电出力，发明了一种将储能系统介质频率具体化的研究方法。文献[14]利用傅里叶分解方法(Fourier decomposition method，FDM)平滑新能源发电因调度产生的不平衡功率，将不平衡功率的高频部分和低频部分分别配置给不同的储能装置，高频部分使用超级电容器进行平滑，低频部分使用蓄电池储能进行平滑。文献[15]利用新能源发电制氢与超级电容器相结合的混合储能形式调节新能源发电机组出力，调节后的新能源发电机组出力平缓，有效减少了新能源波动，达到并网要求。以上文献均为储能的基础配置，并未考虑储能系统的经济性，需要进一步研究。

本文在已有文献的基础上，考虑混合储能平滑新能源发电出力的波动性，基于滑动平均法平滑新能源发电原始出力，将平滑后出力曲线与原始出力曲线之差作为储能参考功率，然后通过经验模态分解(empirical mode decomposition，EMD)将储能参考功率分解为高频部分和低频部分，高频部分通过飞轮储能进行平滑，低频部分通过锂离子电池储能进行平滑，求得混合储能所需容量和功率。最后，通过混合储能系统净收益模型求得系统净收益，验证储能系统经济性。以风电历史数据为新能源发电数据进行算例分析，验证所提方法的有效性，并计算储能系统所需成本。

1 混合储能平滑新能源波动优化配置模型

本文通过滑动平均法确定新能源发电出力的平滑基准，平滑基准需要满足国家对新能源发电并网的相关指标(通常为单位时段的波动率)要求，而后将新能源发电出力的实际数据与所确定的新能源发电出力的平滑基准做差，求得储能参考功率，进而求取储能系统的容量[16]。

1.1 混合储能系统功率分配

本文采用EMD对储能参考功率进行分解，通过分析瞬时频率-时间曲线中相邻本征模态函数(intrinsic mode function，IMF)的模态混叠量进行高频和低频部分的划分[17]。分配后的结果为：

(1)

(2)

式中：Pg为高频部分储能功率；Pd为低频部分储能功率；FIMi为第i个IMF；j为从1到n的正整数，n为全部IMF的数量。

1.2 储能系统充放电功率

由于充放电损耗的存在，其功率可以表示为：

PE(t)=PHESS(t)/ηd,PHESS(t)≥0, 放电；

(3)

PE(t)=PHESS(t)·ηc,PHESS(t)<0, 充电.

(4)

式中：PHESS(t)为t时段电网侧储能功率；PE(t)为t时段系统内储能功率；ηd为储能放电效率；ηc为储能充电效率。

1.3 储能周期电量平衡

在一定时间内，储能的初始能量需要维持在一个固定值，即此段时间储能充放电量之和为0，也就是功率之和为0，可以表示为：

(5)

P′E(t)=PE(t)-ΔP，

(6)

式中：ΔP为储能功率调节量；P′E(t)为t时段修正的储能出力；N为仿真时间内的时段数。则储能额定功率

PEN=maxP′E(t).

(7)

1.4 充放电量计算

通过修正后的储能出力求得储能能量变化曲线，其表达式为

(8)

式中：E(t)为储能各时段电量；Ts为每一功率持续时间。

1.5 额定容量计算

储能的剩余电量情况可以用荷电状态计算，即

(9)

式中：C为各时段荷电状态；C0为储能初始荷电状态；EN为储能额定容量。充电时E(t)为正，储能电量上升，荷电状态相应变大；放电过程相反。

定义Cmax、Cmin分别为储能荷电状态变化的上下限，则

(10)

(11)

能够同时使以上两式成立的最小值即为EN：

(12)

(13)

联立可知

(14)

1.6 初始状态确定

联立式(11)、(12)可计算初始荷电状态

(15)

1.7 储能系统的循环寿命

(16)

Neq=NDDk.

(17)

式中：Neq为100%充放电深度下的储能充放电次数；ND为充放电深度D下的储能充放电次数。

飞轮储能循环寿命只与储能充放电次数相关，由此能够得出飞轮储能循环寿命计算公式为

(18)

式中：Nf为飞轮储能实际使用天数；Nmax为飞轮储能最大充放电次数；Nre为飞轮储能每日充放电次数。

2 混合储能系统净收益模型

2.1 储能成本

本文成本模型基于费用现值法，混合储能系统的预期寿命设为Yr年，基准折现率I，成本系数A=(1+I)-Yr。

初始储能系统成本

W1=A(WpsPEN+WesEN).

(19)

式中：Wps为单位储能功率成本；Wes为单位储能容量成本。

运行维护成本

W2=A(WompPEN+WomeEN).

(20)

式中：Womp为单位储能功率运行维护成本；Wome为单位储能容量运行维护成本。

设备回收残值

W3=αA(W1+W2)，

(21)

式中α为回收利益系数，本文取α=5%。

总成本

WLCC=W1+W2-W3.

(22)

2.2 储能系统收益

减少新能源发电备用容量所获得的收益

(23)

Pd=∑G.

(24)

(25)

式(23)—(25)中：Pd为新能源电场每日旋转备用减少量；βd为新能源电场每日预测置信度；PX(t)为新能源发电在t时段的出力；Sr为新能源电场单位备用容量的费用。

减少新能源并网通道建设所获得的收益

S2=Scmax{0 , maxPX(t)-

max(PX(t)-PHESS(t))},

(26)

式中Sc为单位功率通道建设费用。

综合可得储能系统收益

S=S1+S2，

(27)

进而可得整个系统净收益

Z=S-WLCC.

(28)

3 算例分析

根据所提模型进行储能配置，新能源出力数据采用2018年中国某风电场实际历史数据，风电机组装机容量50 MW。选取其中典型日出力曲线(图1)进行波动平滑。该风电场风电出力具有明显的峰谷特性，和典型日负荷对比还具有反调峰特性。

图1 风电场典型日出力曲线

对风电出力的平滑从以下3个方面进行分析：出力平滑——对比平滑前后风电出力的相关参数；

储能配置——求取混合储能的功率和容量；储能成本——求取混合储能系统成本。

a)出力平滑。本文通过滑动平均法对风电出力进行平滑，平滑后的出力波动明显减小，风电的原始出力和平滑后的对比如图2所示，风电平滑前后的波动数据见表1。

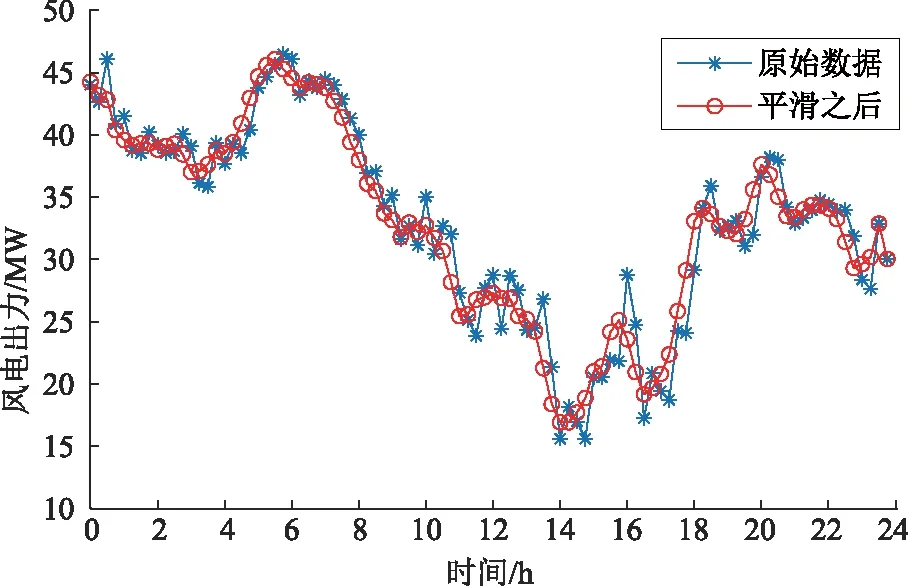
图2 储能加入前后风电出力对比

表1 风电出力波动数据

从表1可以看出平滑后的风电出力各个波动数据都优于平滑前，3项指标明显下降，其中最大波动率下降47%，功率标准差也下降了3.5%。平滑后的风电出力更有利于电网的优化运行。

b)储能配置。通过滑动平均法确定新能源发电出力的基准，将其与新能源发电实际出力做差，求得PHESS的变化数据，对储能参考功率进行EMD，分解后的各部分IMF分量(IMF1—IMF5)如图3所示。可以看出：高频部分的IMF分量波动更加剧烈，适用于功率型储能；低频部分的IMF分量波动缓慢，适用于能量型储能。根据相邻曲线混叠最少原则，通过各IMF的瞬时频率-时间曲线可以将储能参考功率分为高频部分和低频部分。根据式(1)、(2)即可求得储能高频部分的出力和储能参考功率低频部分的出力，高频部分和低频部分储能功率如图4所示。

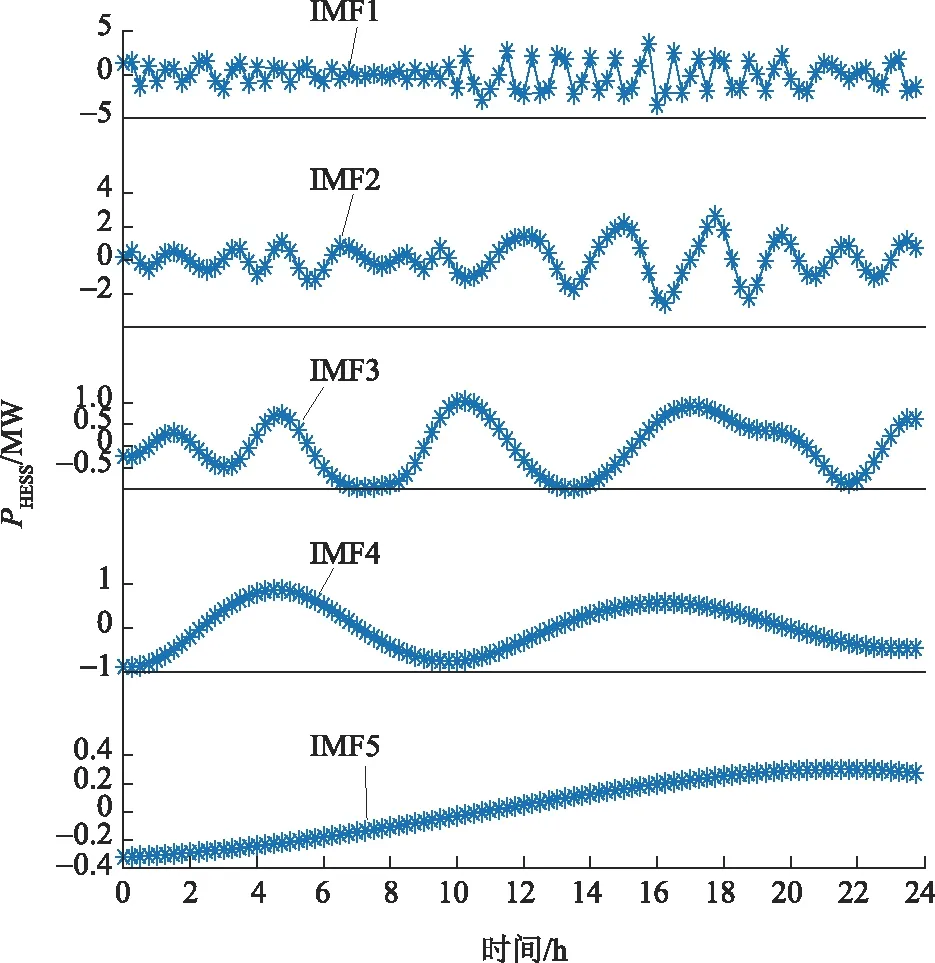
图3 各IMF分量波动曲线

图4 混合储能高频部分和低频部分功率曲线

本文储能配置选取的能量型储能为锂离子电池储能，功率型储能为飞轮储能。根据式(3)—(7)可以求得混合储能的相应功率，根据式(8)—(14)可以求得储能相应部分的容量，储能系统的初始荷电状态由式(15)求得，储能系统功率与容量配置具体结果见表2。可以看出：锂离子储能电池储能容量更大，但功率较小，系统的初始荷电状态也相对较高；飞轮储能系统储能容量较小，但功率较大，初始荷电状态较低。其原因是：储能参考功率的高频部分波动范围更广，且充放电更频繁，使得储能容量长期保持在相对稳定的水平；储能参考功率的低频部分波动范围小，但充放电过程少，储能长期处于放电状态，需要持续输出。

表2 混合储能系统功率与容量配置结果

c)成本求取。锂离子储能和飞轮储能的相关技术参数参考文献[18]。锂离子储能电池100%充放电状态下的循环次数为6 000次，飞轮储能最大充放电次数为500 000次。根据式(16)—(18)计算可得锂离子储能电池运行年限为7.10年，飞轮储能运行年限为30.44年，所以混合储能系统全寿命周期为7.10年。根据式(19)—(22)可以求得锂离子储能成本为4 312.01万元，飞轮储能成本为6 819.98万元，混合储能系统总成本为11 131.99万元。

通过历史数据模拟可得储能系统年收益为3 558.52万元，预计3.12年收回成本，储能系统全寿命周期为7.1年，净收益为14 133.01万元。

4 结论

本文针对新能源发电出力的波动性提出了混合储能的平滑方法，将滑动平均法和EMD相结合，构建储能成本模型，并采用实际数据进行仿真分析。主要得出以下结论：

a)用滑动平均法平滑新能源出力更加简单方便，平滑后的出力曲线更为流畅。

b)通过配置储能系统减小系统备用容量以及减少新能源并网通道，使电网运行效益最大化。

c)通过EMD确定混合储能高频分量和低频分量，高频部分波动剧烈，低频部分波动平缓。

在新能源广泛接入电力系统的现状下，由新能源发电出力的波动性造成的问题会越来越多，为电力系统的持续发展增添了难度。本文在新能源大规模并网的背景下对电力系统可靠性进行研究，在已有科研成果的基础上，进一步探索新能源接入电力系统的可靠性问题，但还存在许多的不确定因素有待展开更深入的研究，具体有以下几点：①新能源发电波动平滑过程中具有出力不确定性；②混合储能平滑新能源波动方面，未考虑储能的寿命损耗；③新能源发电并网时，只研究了系统层面的可靠性变化，并未讨论节点层面的可靠性变化。