考虑风电接入和负荷转供的配电网可靠性成本

甘子莘，荆朝霞

(华南理工大学 电力学院，广东 广州 510641)

《关于进一步深化电力体制改革的若干意见》(中发﹝2015﹞9号文)提出要纵深推进输配电价改革，国家发展改革委在《关于制定地方电网和增量配电网配电价格的指导意见》中规定要加强对配电网的成本、价格监管，形成科学合理、公开透明、激励有效的配电价格[1-4]。因此，配电网的成本核定对电网的发展十分重要。

配电系统是电网中不可缺少的重要部分，电能要安全可靠地输送到终端用户侧，必须经过配电网的连接[5]。由于负荷会发生波动，配电网面临着安全稳定问题，需要关注配电网的最大供电能力(total supply capability，TSC)。TSC是评价配电网的重要指标[6-7]，它是指在所有主变压器(以下简称“主变”)和馈线“N-1”校验均满足时，配电网在一定供电区域内的最大负荷供电能力。目前，配电网TSC的计算方法主要分为解析法和线性规划模型法。解析方法是分析主变接触单元的供电能力和最大负荷率。线性规划模型法是将TSC模型转化为一个线性规划问题，以TSC为目标函数，约束条件包括“N-1”安全准则下的负荷转供约束、下一级配电网的联络结构等。负荷转供是指当故障发生时，故障主变可以通过开关动作将负荷转移到其直接连接的主变上，馈线上的负荷也可以通过开关动作转移到其直接相连的馈线上。负荷转供约束包括主变容量约束和线路容量约束，在考虑了负荷转供后，“N-1”会发生改变，对输配电成本会产生一定的影响，因此需要对这部分成本进行有效分析[8-10]。

目前，国内外的研究主要集中在配电系统安全域的概念、模型以及TSC的计算方法上[11-14]。文献[15]提出基于馈线互联的TSC模型及其计算方法，该模型能准确描述馈线间多段多接线的互联方式，充分反映电网信息，计算结果在考虑主变“N-1”故障的基础上，考虑了馈线“N-1”故障。上述文献主要围绕配电网“N-1”安全校验和TSC模型进行研究，但没有对配电网为了满足“N-1”安全准则而付出的可靠性成本进行定量分析。文献[16]提出配电自动化系统可靠性成本效益综合分析模型，利用缩短停电时间带来的经济效益来衡量供电可靠性的成本和效益，但没有考虑负荷转供对可靠性成本的影响。文献[17]采用序贯蒙特卡罗法来评估可靠性，且重点考虑系统可能出现的单一元件故障，并用停电损失来度量配电网的可靠性成本，但是没有考虑新能源接入对可靠性成本的影响。

因此，本文考虑未来可再生能源增多和负荷转供对配电网可靠性成本的影响，通过TSC模型和用户停电损失费用来计算配电网的可靠性成本，并利用配电网的扩容规划模型，决定风力发电机组的最佳投资时间[18]，分析在风电接入后配电网可靠性成本的变化。

1 配电网“N-1”安全校验

配电网“N-1”安全校验准则是指当配电网中的任一独立元件如主变、馈线等发生故障时，不会造成其他变压器或线路过负载，从而不会发生不必要的停电，它是配电网维持安全稳定运行的一个重要准则。“N-1”安全校验主要有2种：主变“N-1”和馈线“N-1”。

主变“N-1”是指在给定负荷状态下，当某台主变发生故障时，负荷均可以在满足其他主变容量约束和馈线容量约束的前提下，通过站内或站外的联络线进行转供。主变“N-1”需要遵循以下原则：

a)主变在同一变电所内优先进行负荷转供。对于具备2台以上主变的变电所，应优先考虑负荷充裕度大的主变。

b)如果站内主变不能成功对负荷进行转供，则需要依靠站外与该主变相连的馈线来进行转供。当主变有多条出线时，负荷小的馈线优先转供。

馈线“N-1”校验是指在馈线的任何位置发生故障时，检查故障是否能被隔离，并将供电负荷转移到其他连接的馈线上。由于配电网规模较大，在规划中对整个网络进行“N-1”验证是不现实的，因馈线出口发生故障造成的后果很严重，故通常仅验证馈线出口故障。在馈线上执行“N-1”校准时，每个馈线的转移负载应小于其自身的馈线容量。

2 基于主变的TSC模型

配电网的实际运行约束条件应在“N-1”校验时得到考虑，例如主变和馈线之间的负载转移、网络中主变和馈线之间的连接关系等。在TSC模型的计算过程中，除了配电网络的总体TSC之外，还需要计算到达TSC时每个主变和馈线的负荷分布[19-20]。

2.1 配电系统安全域

在配电系统中，工作点是指配电网在某一时刻所有状态量的集合，这里用主变所带负荷来表示。配电系统的安全域是指在配电网的主变“N-1”和馈线“N-1”的约束下，配电网络可以安全稳定运行，所有工作点共同形成配电系统的安全域。工作点可以表示成n维向量的形式，即

T=(P1,P2,…,Pn)T.

(1)

式中Pi为第i台主变所带的负荷，i=1,2,…,n。

在配电网运行中，负荷转供会受到馈线容量和主变容量的约束，转供完成后主变和馈线所带的负荷都不能超出它们的承受范围，这些约束决定了配电系统的安全域边界。所以，配电系统安全域的模型可表示为：

(2)

(3)

Fmk,tr+Fk≤Rk,m(∀m,k),

(4)

tij,tr+Pj≤Rj(∀i,j).

(5)

式中：Fm为馈线m所带的馈线出口负荷，Fk为馈线k所带的馈线出口负荷；Fmk,tr为馈线m发生“N-1”故障时转供给馈线k的负荷；Pi为主变i所带的负荷，Pj为主变j所带的负荷；tij,tr表示当主变i发生“N-1”故障时转供到主变j的负荷量；Fm∈Gi表示馈线m的出口负荷出自主变i，Fk∈Gj表示馈线k的出口负荷出自主变j；Rk,m为馈线k的容量，也反映了馈线m和馈线k之间存在转供关系；Rj为主变j的额定容量。

在配电系统安全域模型中，式(2)为主变和馈线之间的等式约束；式(3)为主变发生“N-1”故障时的馈线负荷转供等式约束；式(4)为馈线“N-1”约束；式(5)为主变“N-1”约束。

2.2 主变联络关系

2个主变之间的联络关系意味着在“N-1”的情况下，某个特定主变所承载的负载可以通过联络开关的作用转移到另一个主变上。主变所带负荷可通过联络母线或者馈线的开关动作来进行转移，因此联络形式可归纳为2种——变电站的站内联络和电网线路间的联络，分别用以分析变电站站内供电能力和电网负荷转供能力。

引入主变联络矩阵L来表示主变之间的联络关系，设区域内有n台主变，将其分别编号为1,2,…,n，给出主变联络矩阵

(6)

式中Lij为主变i和j之间的联络关系，若2台主变有联络，Lij=1，否则Lij=0。

2.3 基于主变互联的TSC模型

在综合考虑主变“N-1”和馈线“N-1”故障后，根据配电系统安全域模型建立基于主变互联的TSC模型，其目标函数为

(7)

式中ZTSC为配电网的最大供电能力。

模型约束为式(2)—式(5)。

上述模型考虑的是故障发生后，配电网可以继续运行的情况。当主变发生故障时，其具有短期过载能力，时间越短，过载能力越强。智能电网环境下实现配电自动化后，中压配电网具有更快的负荷传递能力，主变的过载时间将大大缩短。这时，同一变电站的无故障主变能够承受故障主变的满负荷，过载系数不会影响模型计算出的最大供电能力。在引入主变联络矩阵L后，式(5)转化为：

Lijtij,tr+Pj≤Rj(∀i,j).

(8)

同样地，当主变间存在联络关系时，Lij=1，否则Lij=0。

2.4 配电网在“N-1”安全准则下的可靠性成本

电力系统除了提供电能的传输服务，还必须保证一定的可靠性，保证可靠性需要花费一定的成本，即可靠性成本。要保证系统的可靠性，可以选择采取短期或者长期措施。短期措施是指采用调频、调压等辅助服务来保证可靠性；长期措施是指通过投资建设来预留充足的容量来保证可靠性。

在配电网中，为了保证可靠性，需要投资巨大的建设成本来保证配电网线路和变压器容量的充足，具有显著的规模经济特性。这部分固定成本与电能的使用量无关，只与厂家前期的投资有关。为了满足“N-1”安全校验，配电网需要预留一定的容量裕度，在任意一台主变或者任意一条线路发生故障时，系统的可靠性能得到保证，但这同时也产生了可靠性成本。本文利用停电损失费用对可靠性成本进行定量计算。如果不考虑“N-1”安全准则，配电网可能会由于主变、馈线等发生故障而导致停电，从而造成一定的经济损失；如果考虑“N-1”准则，故障停电发生概率会下降，但最大供电能力也会减小，且一般要比总额定容量小。因此，两者之间的差额容量所对应的停电损失费用可以较好地反映可靠性成本。计算过程如下：

Cq=(δ0-δq)×Wq×ΔT×qr.

(9)

式中：Cq为停电损失费用；δ0为不考虑“N-1”时的负荷率；δq为考虑了“N-1”后的负荷率；ΔT为考虑了无“N-1”时故障停电的年平均停电时间增加值；Wq为配电网变电站的总容量；qr为故障停电的单位电量停电成本。

3 配电网扩容规划模型

配电网的最大供电能力会受到诸如变压器容量、线路容量和电网结构等因素的影响，本章将建立配电网的扩容规划模型，主要思路是在变压器容量、线路容量等约束下，通过接入风力发电机组使得最大供电能力得以提高，从而降低配电网的运行成本。

3.1 风电机组出力水平确定

风速的间歇性和随机性会导致风力发电机组的输出功率具有不确定性[21-23]，文献[24]认为使用Beta分布对风电出力概率密度函数进行拟合效果更好，并且更加符合实际情况。Beta分布中的参数可以灵活变化，能反映不同情况下的风电出力，其自变量取值为0～1区间，恰好能够表示标幺化后的风电机组出力大小。所以，本文用Beta函数来表示风电出力概率密度函数，Beta分布的概率密度函数为

(10)

式中：q为风电机组输出功率的标幺值，是服从Beta分布的随机变量；α和β为Beta分布的分布参数；B(α,β)的值可以由预测均值μ和预测误差的方差σ2来确定，表达式如下：

(11)

(12)

3.2 风电机组投资时间确定

在实际投资t年份内，配电网中的风电机组未来投资成本现值

(13)

式中：Ca为风电机组的投资等值成本；d为贴现率。

如果没有进行配电网扩容规划，那么配电网的供电能力会受到TSC的制约。随着居民用电负荷的增长，线路和变压器在负荷高峰时刻也需要超出配电网的安全供电范围来运行，这样会导致用户停电的风险加大，由此而造成的停电损失费用现值

(14)

当停电损失费用现值不小于未来投资成本现值时，应该对配电网进行投资，建设风力发电机组来增加配电网的最大供电能力，此时对应的投资年份数为t。

4 算例分析

图1为算例分析图，图中S1—S6表示变压器，M1—M6表示母线。该算例中共有3座110 kV变电站和28回10 kV馈线，变电站总容量为120 MVA，各变压器的额定容量为20 MVA，馈线总容量为252 MVA，每条馈线容量均取9 MVA。

图1 算例分析图

假设在不考虑“N-1”的情况下，配电网的负荷率为1，年平均停电时间增加值ΔT为0.5 h，故障停电的单位电量停电成本为qr为25元/kWh。

4.1 TSC的计算

在2.3节所建模型的基础上，利用Lingo软件求解，得到TSC为92.66 MVA，变压器的平均负载率为77.22%。达到TSC时的工作点T=(16.33,16.33,16.33,16.33,12.67,14.67)T，当取TSC工作点时，系统处于临界通过状态，即系统的“N-1”校验恰好处于通过与不通过的临界状态，如果任意主变或馈线再增加一点负荷，系统就不能通过“N-1”安全性校验。在达到TSC工作点时，各馈线分配的负荷见表1。

表1 达到TSC时的馈线负荷值

表1所示为在变电站达到TSC时各馈线出口段的负荷，从表1可以看到馈线4、6、11、14和28所带负荷为0，这是因为使用Lingo求解出来的是一个可行的分配方案，但并不唯一。

由于电力系统是由成千上万的设备所构成，从可靠性角度来看，必然存在一定的故障率。为了满足主变和馈线发生“N-1”故障时的负荷转供约束，变压器不能满载，剩下未被使用的27.34 MVA容量相当于留作备用的容量，可提高系统的稳定和供电可靠性。这部分容量所产生的是输电成本里的可靠性成本，即为保证可靠性而支付的费用和因安全问题而产生的损失。因此，在考虑了负荷转供后，根据式(9)计算得到算例电网每年产生的总可靠性成本为341 750元，在考虑了负荷转供需要满足的“N-1”准则后，输配电成本因为可靠性需求而增加了。

4.2 风力机组的投资运行

考虑在母线M1处接入1台5 MW的风力发电机，风电满足α=2.65和β=2.4的Beta概率密度函数，如图2所示。

图2 Beta概率密度函数图

根据Beta分布的概率密度函数，得到风电机组的出力预测值为2.624 MW。假设总负荷以每年5%的速度增长，年平均停电时间增加值ΔT每年也增大5%。风力发电机组的容量成本为2 600 000元/MW，机组安装成本为550 000元/MW，贴现率d=6.3%。根据式(14)可以得到停电损失费用现值Cg随年份数t的增长曲线如图3所示。

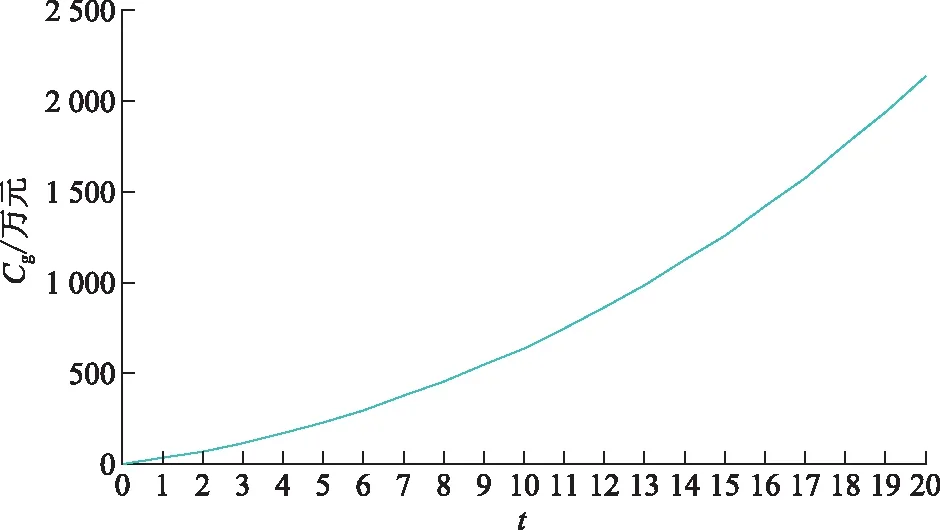
图3 停电损失费用现值随年份增长曲线

由图3可以看出，在风电机组投资运行之前，随着年份数的增长，配电网的停电损失费用现值不断增加，且增长速度逐渐加快。

根据式(13)可以得出投资成本现值Cnow随t变化的曲线，并结合停电损失费用现值Cg曲线来分析风电机组的最佳投产时间，如图4所示。

由图4可以看出，风电机组投资成本现值随着年份的增加而减小，而停电损失费用现值则随着年份的增加而增加。2条曲线的交汇点时间为11.9，也就是说在投资11.9年后，停电损失费用将会超过风电机组投资成本现值，此时对配电网进行风力发电机组投资建设来增加配电网的TSC，更具有经济性。

图4 投资成本现值和停电损失费用现值曲线

在建设了5 MW的风力发电机组后，配电网的最大供电能力由原来的92.66 MVA提高到94.94 MVA，达到TSC时的工作点T1=(19.31,16.68,15.63,15.63,14.32,13.37)T，此时，配电网每年的可靠性成本减少为313 250元。投资建设5 MW风电机组前后的可靠性成本分别为341 750元和313 250元。因此，建设5 MW风电机组可以使得配电网每年的可靠性成本降低28 500元，有利于配电网的长期经济稳定运行。

由算例可以看出，配电网为了满足“N-1”安全检测，需要付出相应的可靠性成本，而在配电网中接入风电机组，可以增加配电网的TSC和可靠性，从而减少可靠性成本。

5 结束语

在电力系统中，配电系统是一个重要的组成部分，也是确保用电安全可靠的关键一环。本文研究了风电接入和负荷转供对输配电成本的影响。在考虑了负荷的一次转供后，配电网的TSC也会相应降低，配电网需要承担一定的可靠性成本，来满足“N-1”安全检验的需求。这部分可靠性成本高，因此需要考虑对配电网进行扩容规划。通过对比接入发电机组的未来投资成本现值和停电损失费用现值的大小关系，进一步确定配电网的最佳投资时间，实现成本最小化。算例分析结果表明，发电机的接入会使配电网的TSC得到提升，从而有效地降低配电网的可靠性成本。