规模化养殖罗曼粉商品蛋鸡产蛋率和累计产蛋数曲线拟合分析
2021-08-31植石全张恒通韦武奇李晓阳
植石全,张恒通,韦武奇,李晓阳
(广东绿杨农业股份有限公司,广东 茂名 525243)
蛋鸡养殖产业是我国畜牧业重要产业之一。近年来,随着机械化程度和饲养管理水平的提升,越来越多的企业采用了规模化密闭式的蛋鸡养殖方式, 而由于长期以来我国的蛋鸡养殖是以单栋在万羽以下的中小规模养殖为主, 鲜见对单栋5万羽以上规模化蛋鸡场的研究。 蛋鸡的产蛋性能存在一定规律, 产蛋性能规律可以反映鸡群产蛋是否异常, 能够指导管理者及时发现和解决蛋鸡的产蛋问题,避免不必要的损失,对保障鸡群产蛋性能的稳定和提高蛋鸡场生产效益具有重要意义。 有许多学者对产蛋率曲线模型进行了研究,而目前应用最广泛的产蛋率曲线模型有3 种,分别是分室模型、杨宁模型和伍德模型[1-2]。 有研究表明,不同品种或品系的产蛋率最佳曲线模型是有差异的,需进行家禽试验加以验证[3-4]。 可以通过产蛋率曲线预测鸡群不同产蛋阶段的产蛋特点, 但产蛋率模型并不能反映鸡群的实际累计产蛋数及产蛋拐点[5-6]。Bertalanffy、Gompertz 和Logistic 3 种模型曲线能够对鸡群实际累计产蛋数进行拟合[7],而3 种模型对累计产蛋数的拟合效果是有差异的[8-9]。 罗曼粉蛋鸡具有成活率高、料蛋比低、产蛋率高以及产蛋稳定等优点, 是一种适合规模化养殖的商品蛋鸡。由于试验条件的不同,产蛋性能曲线模型拟合的效果各异, 需要通过规模化商品蛋鸡试验加以验证。 该研究对单栋9 万羽罗曼粉蛋鸡18~85 周龄产蛋情况进行了梳理, 并对其进行了相关性分析。 采用分室模型、杨宁模型、伍德模型对罗曼粉商品蛋鸡的产蛋率进行拟合分析,用Bertalanffy、Gompertz、Logistic 等 模 型 对 蛋鸡的累计产蛋数进行拟合分析, 以期为规模化养殖罗曼粉商品蛋鸡的营养水平及饲养管理提供科学依据。
1 材料与方法
1.1 试验动物及饲养管理
选择来自广东杨氏农业有限公司9 万羽1 日龄的罗曼粉蛋鸡雏鸡,1~16 周龄饲养在育雏舍(采用十列五层六走道层叠式的笼养模式),17~85周龄饲养在蛋鸡舍(采用十列八层六走道层叠式的笼养模式)。按照《培育高产商品蛋鸡手册》进行免疫程序和饲养管理,18 周龄后对罗曼粉蛋鸡的产蛋情况进行监测。
1.2 产蛋性能统计
以周为单位统计罗曼粉蛋鸡产蛋率及累计产蛋数,记录18~85 周龄罗曼粉蛋鸡的产蛋情况:
日产蛋率 (%)=每天产蛋数 (枚)/当日存栏(羽)×100%;
周产蛋率(%)=每周产蛋率之和/7×100%;
日产蛋数(枚/羽)=每天蛋数(枚)/入舍母鸡数(羽);
累计周产蛋数 (枚/羽)=开始产蛋周产蛋数(枚/羽)+...+结束产蛋周产蛋数(枚/羽)。
1.3 统计与分析
1.3.1 产蛋率常用曲线的拟合模型 分室模型、杨宁模型和伍德模型是产蛋率常用的曲线拟合模型,以下为3 种模型的具体公式:
分室模型:Y(t)=a×(1-e-c(t-d))×e-b×t;
杨宁模型:Y(t)=(a×e-b×t)/(1+e-c×(t-d));
伍德模型:Y(t)=a×tb×e-c×t。
以上各式中,a、b、c 和d 为待定参数,t 为产蛋周龄,Y(t)为第t 周的周产蛋率[8]。
1.3.2 累计产蛋数常用曲线的拟合模型 Bertalanffy、Gompertz 和Logistic 是累计产 蛋数常用曲线的拟合模型,以下为3 种模型的具体公式:
Bertalanffy:Y(t)=A×(1-B×e-K×t)3;
Gompertz:Y(t)=A×e-B×exp(-K×t);
Logistic:Y(t)=A/(1+B×e-K×t)。
以上各式中,A 为极限产蛋数,B 为待定参数,K 为接近极限速度,t 为产蛋周龄,Y(t)为累计产蛋数。 其中,3 种模型拐点周龄分别为(ln3×B)/K、(lnB)/K、(lnB)/K,拐点产蛋数分别为8A/27、A/e、A/2[8]。
1.4 数据统计分析
试验数据使用Excel 2016 软件进行整理,各常用的拟合模型参数值由SPSS 20.0 中的非线性回归计算得出,曲线用origin 2020 绘制。
2 结果与分析
2.1 罗曼粉蛋鸡产蛋率
2.1.1 罗曼粉蛋鸡的周产蛋率 由图1 可知,罗曼粉蛋鸡在18~23 周龄产蛋率迅速上升;24 周龄进入产蛋高峰期, 产蛋率在90%以上的持续时间为25 周龄,27 周龄达到产蛋高峰期, 产蛋率为96.39%;48 周龄后产蛋率缓慢下降,49~83 周龄产蛋率80%~90%;84 周龄后,周产蛋率降到80%以下。

图1 罗曼粉商品蛋鸡周产蛋率的变化曲线
2.1.2 常用产蛋率拟合模型参数估计值与拟合度由表1 可知,将各个参数代入模型方程可得:

表1 产蛋率拟合模型参数估计值与拟合度
分室模型:Y(t)=111.862×(1-e-0.296×(t-18.429))×e-0.004×t;
杨宁模型:Y (t)=(105.666×e-0.003×t)/(1+e-1.191×(t-21.237));
伍德模型:Y(t)=0.791×t1.664×e-0.034×t。
分室模型的拟合度为0.935,杨宁模型的拟合度为0.997,伍德模型的拟合度为0.450。 可见,分室模型和杨宁模型都适合运用于罗曼粉蛋鸡产蛋率的预测,杨宁模型的预测效果最好,而伍德模型的预测效果是最差的。
2.1.3 罗曼粉蛋鸡产蛋率实际观测值与拟合值比较 由表2 可知, 实测最高周产蛋率为96.39%,出现在27 周龄; 分室模型的拟合最高产蛋率为96.72%,出现在33 周,与实测周产蛋率、时间分别相差0.34%、6 周; 杨宁模型的拟合最高周产蛋率为97.40%,出现在26 周,与实测周产蛋率、时间分别相差1.05%、1 周; 伍德模型的拟合最高周产蛋率为97.08%,出现在49 周,与实测周产蛋率、时间分别相差0.72%、22 周。 3 种模型的最高产蛋率相差不大, 但在杨宁模型下出现最高产蛋率的时间与实测值最接近。由图2 可知,杨宁模型预测周产蛋率与实测周产蛋率的曲线更趋于一致,拟合度达到了0.997;伍德模型预测周产蛋率与实测周产蛋率的曲线相对一致,拟合度为0.935;伍德模型预测周产蛋率与实测周产蛋率的曲线区别较大,拟合度只有0.450。综上,杨宁模型是预测罗曼粉蛋鸡周产蛋率的最佳拟合模型。
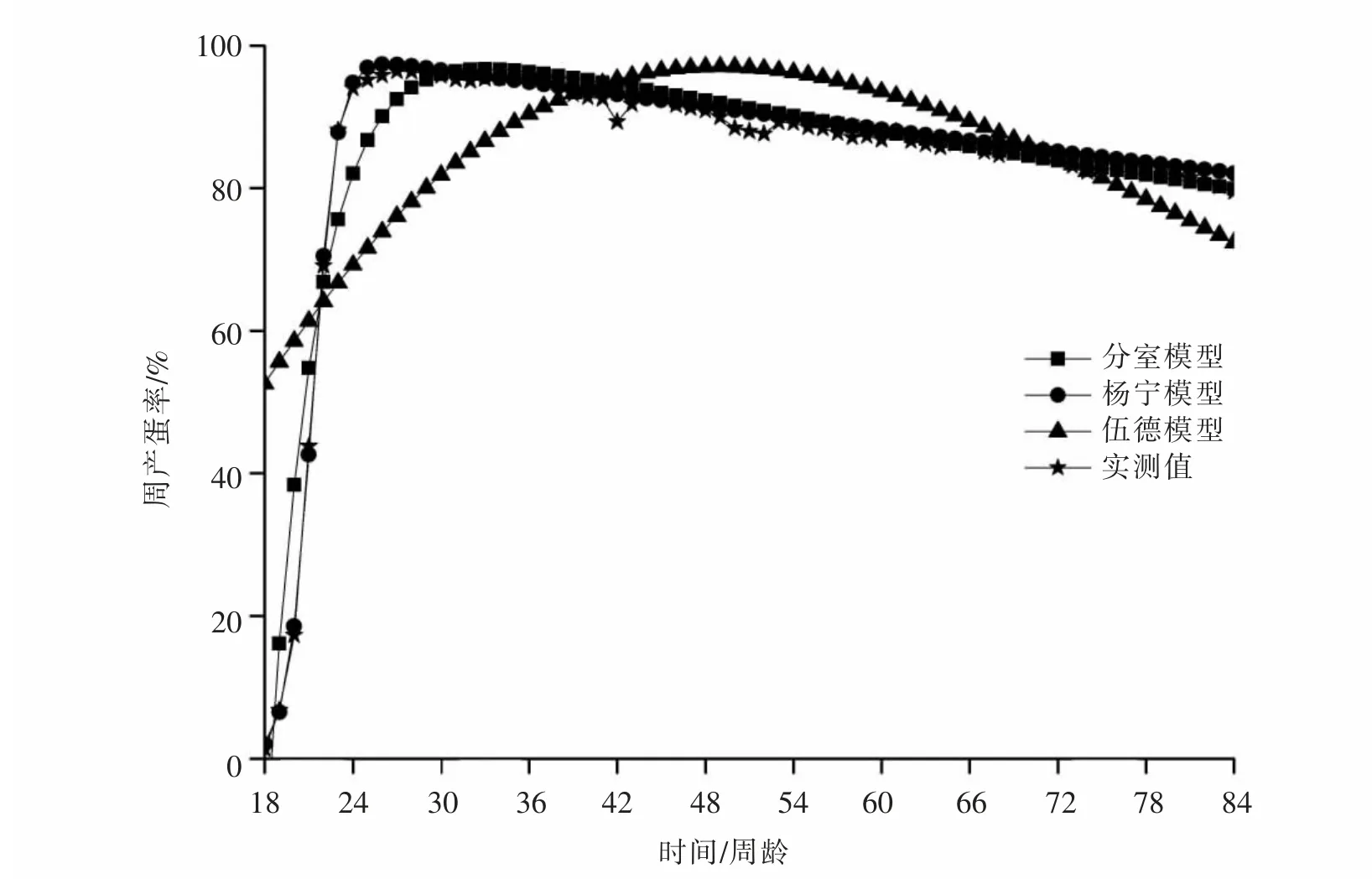
图2 3 种产蛋率拟合模型曲线与实际产蛋率曲线的比较

表2 3 种周产蛋率模型预测值与实测值的比较 单位:%
2.2 罗曼粉蛋鸡累计产蛋数
2.2.1 常用累计产蛋数拟合模型参数估计值与拟合度 由表3 可知,将各个参数代入模型方程可得:

表3 累计产蛋数拟合模型参数估计值与拟合度
Bertalanffy:Y(t)=510.417×(1-1.237×e-0.029×t)3;
Gompertz:Y(t)=452.203×e-6.978×exp(-0.041×t);
Logistic:Y(t)=388.504/(1+49.788×e-0.075×t)。
Bertalanffy 模型的拟合度为0.998,Gompertz模型的拟合度为0.996,Logistic 模型的拟合度为0.989。可见,Bertalanffy 和Gompertz 更适合运用于罗曼粉蛋鸡累计产蛋数的预测。 但Bertalanffy 利用(ln3×B)/K 和(8A/27)计算所得拐点周龄和拐点累计产蛋数分别为46.861 周龄和151.235 枚,而公式计算值为162.042 枚,相差较大。 Gompertz 利用(lnB)/K 和(A/e)计算所得拐点周龄和拐点累计产蛋数分别为47.384 周龄和166.356 枚, 与公式计算值(166.353 枚)最吻合。
2.2.2 罗曼粉蛋鸡产蛋数实际观测值与拟合值比较 由表4 可知,3 种模型在产蛋的前7 周预测值与实测值的偏差较大, 而Bertalanffy 模型和Gompertz 模型的偏差相对较小, 之后3 种模型都趋近实测值。 由表4 和图3 可知,3 种模型的85周累计产蛋数均低于实测值376.76 枚,Bertalanffy为365.74 枚,Gompertz 为365.12 枚,Logistic 为358.13 枚。 Bertalanffy 和Gompertz 均接近85 周累计实际产蛋数。 整体来看,Bertalanffy 模型和Gompertz 模型的预测图都接近实测图, 两者差异不大。

图3 3 种累计产蛋数拟合模型曲线与实际产蛋率曲线的比较
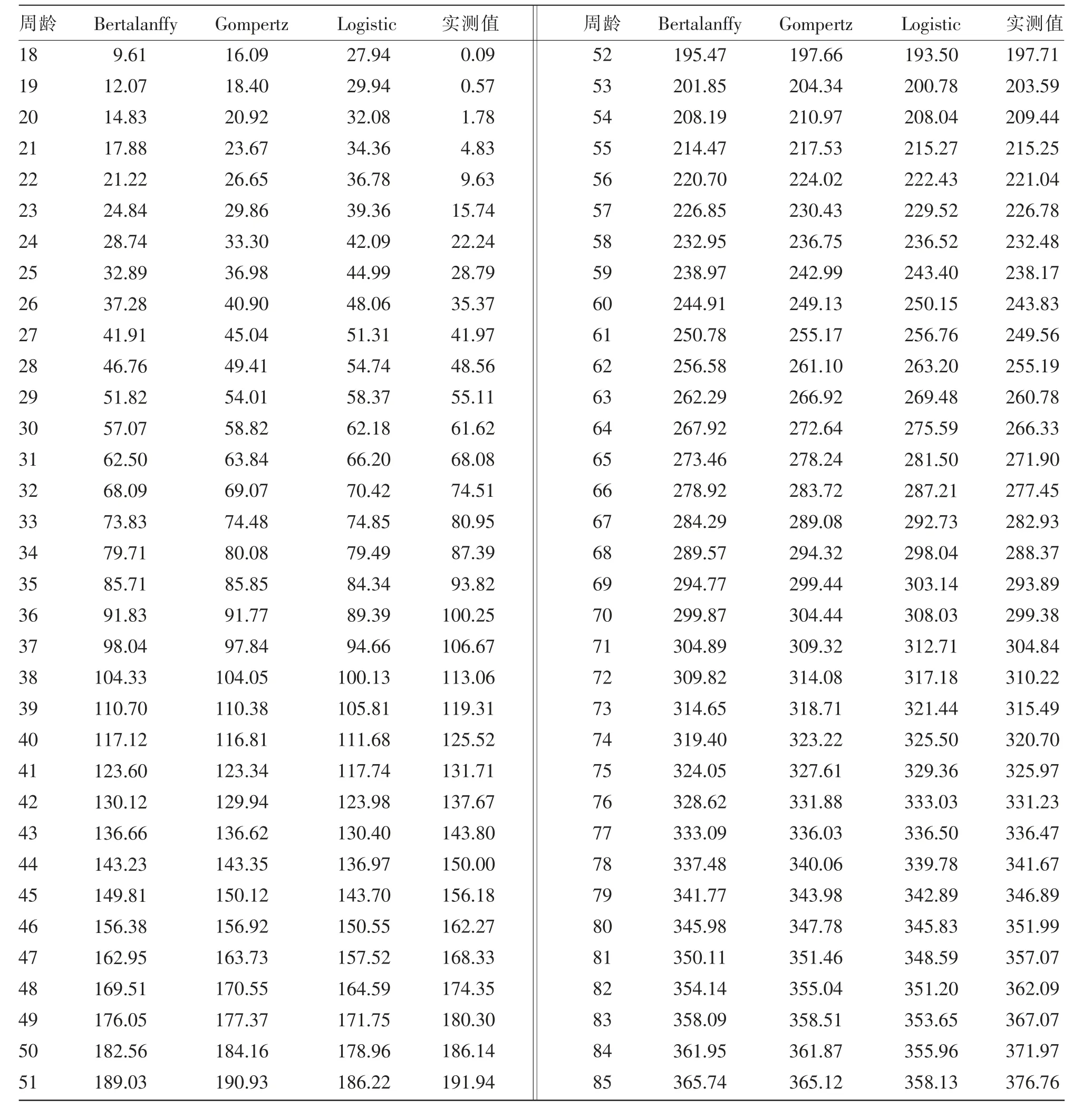
表4 3 种累计产蛋数模型预测值与实测值的比较 单位:枚
3 讨论
鸡的产蛋性能是反映一个品种是否适合做规模化商品蛋鸡的重要指标。 产蛋曲线拟合分析能表明鸡群产蛋随周龄变化的规律, 指导管理者关注蛋鸡的营养和饲养管理水平, 提高鸡群的产蛋性能[10-11]。 该研究使用了分室、杨宁和伍德模型对规模化商品罗曼粉蛋鸡进行了产蛋率拟合和分析。 结果表明,分室模型、杨宁模型和伍德模型的拟合度分别为0.935、0.997 和0.450, 产蛋高峰值分别出现在29、26 和49 周龄,产蛋高峰持续时间分别为29、30 和30 周,而实测的产蛋高峰值出现在27 周龄,高峰持续时间为25 周,因此,分室模型和杨宁模型均能很好拟合商品罗曼粉蛋鸡的产蛋率曲线,杨宁模型的拟合效果最好。 黄俻华等[5]以伍德模型、 分室模型和杨宁模型对彭县黄鸡产蛋率进行曲线拟合分析, 发现3 种拟合模型拟合度分别为0.787、0.908 和0.968, 实测值的产蛋高峰值与产蛋高峰周分别为68.59%和28 周, 杨宁模型的产蛋高峰值 (68.97%) 与产蛋高峰周(28周)最相近;刘嘉等[6]用伍德模型、分室模型、杨宁模型、 三次方程等4 种产蛋模型拟合旧院黑鸡的
产蛋率曲线,研究结果表明,杨宁模型的拟合度最优(0.935),最高峰产蛋的周龄(27 周龄)出现也是最接近实测周(28 周龄);腾军等[10]采用伍德、分室、杨宁、三次方程4 种模型对济宁百日鸡进行产蛋率的曲线拟合分析,4 种模型的拟合度分别为0.699、0.891、0.990 和0.887,杨宁模型的最高产蛋率与实测值仅相差1.18%, 而且都出现在第25周,杨宁模型与实测值曲线基本一致,拟合效果是最好的。以上结果与该试验基本一致,杨宁模型的拟合效果最符合实际产蛋率曲线。 而冯敏山等[12]研究结果表明, 杨宁模型不一定是最符合产蛋率曲线拟合分析,AA 父母代肉鸡产蛋率曲线拟合最好是分室模型, 次之是杨宁模型, 最差是伍德模型;而陆雪林等[13]对2 种山鸡产蛋率的曲线拟合得到相似的结果,认为分室模型的拟合效果最好,更能代表山鸡实测值的曲线拟合, 这与该试验结果不一致,可能是饲粮组成、饲养环境以及品种和产蛋周龄数等因素造成的。
要完整掌握鸡群的产蛋性能规律, 除了掌握产蛋率曲线模型, 还必须掌握鸡群的累计产蛋数模型以及产蛋拐点。在实际生产中,人们往往比较关注的是鸡群整个产蛋期的累计产蛋数, 它更能直接代表整个鸡群的经济价值[14]。 该研究运用了Bertalanffy、Gompertz、Logistic 等 模 型 对 商 品 罗 曼粉蛋鸡进行了累计产蛋数拟合和分析,结果发现,Bertalanffy、Gompertz 和Logistic 3 种模型都能较好对罗曼粉蛋鸡进行拟合分析, 拟合度分别为0.998、0.996 和0.989,3 种模型的极限产蛋数均较实测值(376.76 枚)偏低,其中Bertalanffy 模型和Gompertz 的极限产蛋数 (分别为365.74 枚和365.12 枚)最接近,拐点产蛋周都在47 周左右,但Bertalanffy 模型利用公式与方程所得的拐点产蛋数不一致,公式为151.235 枚,方程为162.042 枚,而47 周龄的实测值为168.33 枚。 综合拟合度和拐点周龄的情况,Gompertz 模型对罗曼粉蛋鸡累计产蛋数的拟合更符合实际预测值。 张学余等[15]对苏禽乌骨鸡进行累计产蛋数曲线拟合分析的研究表明,相对于Gompertz、Logistic 2 种累计产蛋数曲线模型,Bertalanffy 模型的拟合效果更符合实测值的曲线,极限产蛋数为199.14 枚,拐点为产蛋后3.83 周,拐点产蛋数为60 枚,与实测值相当。殷建玫等[16]对狼山鸡的累计产蛋数也有类似的研究。 付亚伟等[8]以Bertalanffy、Gompertz 和Logistic 3 种模型对豫粉1 号蛋鸡进行累计产蛋数曲线拟合分析, 研究结果表明,Bertalanffy、Gompertz 和Logistic 3 种模型对豫粉1 号蛋鸡都有很好的拟合效果,曲线拟合度都在0.98 以上,但在拟合度、产蛋拐点以及拐点产蛋数方面考虑,Gompertz 模型比Bertalanffy 和Logistic 2 种模型更能代表实测值的曲线拟合效果。 该试验与张学余等[15]和殷建玫等[16]的研究结果不一致,而与付亚伟等[8]研究结果一致。 其原因可能是研究的对象品种有差异和生产条件不同。 通过累计产蛋数曲线拟合模型预测鸡群的产蛋拐点周龄, 能够提早采取优化饲养管理、平衡饲料营养等措施推迟产蛋拐点周龄;同时,拐点周龄过后需防止产蛋鸡过肥,通过控制鸡群饲料的摄入量和营养水平提高鸡群后期的生产效益[17]。
4 结论
杨宁模型和Gompertz 模型分别对罗曼粉蛋鸡产蛋率和累计产蛋数的拟合效果最佳, 拟合度分别为0.997 和0.998。 在规模化养殖蛋鸡生产中, 这两种模型适用于对罗曼粉商品蛋鸡产蛋规律的估计和预测, 可用于指导商品罗曼粉蛋鸡的生产实践。
