图的哈密尔顿路指数
2021-08-31牛兆宏乔娟娟
牛兆宏,乔娟娟
(山西大学 数学科学学院,山西 太原 030006)
0 引言
本文考虑的图均为有限无向无环的图,允许有重边。 空图是指没有任何边的图。 文中未定义的术语和符号参见文献[1]。
图G的线图,记为L(G),是指以G的边集为顶点集,且两个顶点邻接当且仅当它们在G中(作为边)是邻接的。 设T是图G中的一条迹,当T的起点和终点重合时,称T是闭迹。 若G的每条边至少关联T的一个顶点时,称T是控制的。 Harary 和Nash⁃Williams 在文献[2]中给出了线图L(G)是哈密尔顿的,原图G的一个特征刻画。
定 理1[2]设 图G是 一 个 边 数 大 于 等 于3 的 连通图。 线图L(G)是哈密尔顿的当且仅当G有一条控制闭迹。
对于整数n≥1,图G的n次迭代线图Ln(G)递归地定义为L(Ln-1(G)),其中L0(G)=G且L1(G)=L(G)。 Chartrand 在 文 献[3]中 研 究 了Ln(G)的哈密尔顿性,并引入了哈密尔顿指数,记作h(G),是使得Ln(G)是哈密尔顿的最小整数n。他证明了对于除去路之外的所有的图,哈密尔顿指数总是存在的。 此后,人们对于图的哈密尔顿指数进行了大量的研究。 Chartrand 和Wall 在文献[4]中研究了树(除路外)的哈密尔顿指数。Ryjáček 等在文献[5]中证明了确定一个图的哈密尔顿指数小于或等于一个给定常数的问题是NP-完全的。 在文献[6]和[7]中,Misra 等和Philip 等分别研究了哈密尔顿指数的算法,并且讨论了算法的时间复杂度。 刘霞和熊黎明在文献[8]中研究了哈密尔顿指数h(G)≤k时的禁用子图集。 其他关于哈密尔顿指数的相关结果,参见综述文献[9]。
记Vi(G)={v∈V(G):dG(v)=i} 和W(G)=V(G)V2(G)。G的枝是一条非平凡的路,它的端点在W(G) 中且内部顶点(如果有的话)在V2(G)中。 用B(G)表示G中所有的枝构成的集合,并且记
B1(G)={b∈B(G):V(b)∩V1(G)≠∅}。在图G中,我们用O(G)表示G中的奇度顶点的集合。 熊黎明和刘展鸿在文献[10]中定义了下面的集合EUk(G),并且给出了迭代线图Ln(G)是哈密尔顿的,原图G的一个特征刻画。
设EUk(G)是图G中满足如下条件的子图H构成的集合:
(I)|O(H)|=0;
(III)对于H的任意子图H1,有dG(H1,H-H1)≤k-1;
(IV)对于每个枝b∈B(G)且E(b)∩E(H)=∅,有|E(b)| ≤k+1;
(V)对于每个枝b∈B1(G),有|E(b)| ≤k。
定理2[10]设图G是一个边数大于等于3 的连通图,n≥2。 那么Ln(G)是哈密尔顿的当且仅当EUn(G)≠∅。
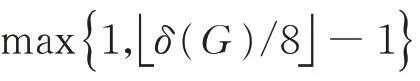
牛兆宏等在文献[14]中,研究了迭代线图Ln(G)的可迹性问题,并且证明了如下的定理3。使得Ln(G)可迹的最小整数n称为图G的哈密尔顿路指数,记作hp(G)。 令EUPk(G)是图G中满足(II)-(IV)和如下条件(I)′和(V)′的子图H构成的集合。 显然,EUk(G)⊆EUPk(G)。
(I)′|O(H)| ≤2;
(V)′ 对于每个枝b∈B1(G)且E(b)∩E(H)=∅,有|E(b)| ≤k。
定理3[14]设图G是一个边数大于等于3 的连通 图,n≥2。 那 么Ln(G) 是 可 迹 的 当 且 仅 当EUPn(G)≠∅。
显 然hp(G)≤h(G)。 文 献[14]中 说 明 了hp(G)的这个平凡上界是最好可能的,并且给出了一些基于其他条件的最好可能的上界。
在定理2 的基础上,人们给出了许多哈密尔顿指数的准确值和上界。 在这些结果中,枝键、圈块作为有效的研究工具被广泛使用。 本文中,我们借助于定理3 中给出的特征刻画,将之前若干哈密尔顿指数的准确值和上界推广到了哈密尔顿路指数上,给出了一些新的结果。
1 哈密尔顿路指数的准确值
这一节我们主要给出几个有关哈密尔顿路指数的准确值。 首先我们给出一些必要的定义,以及Chartrand 和Wall 证明的关于树的哈密尔顿指数的一个结果。
定义CB(G)={b∈B(G):b的每一条边都是G的割边},和CB1(G)=B1(G)。
设G是一个图。 如果G是2-连通的,规定k(G)=0;如果G不是2-连通的并且CB(G)=∅,规定k(G)=1;否则的话,
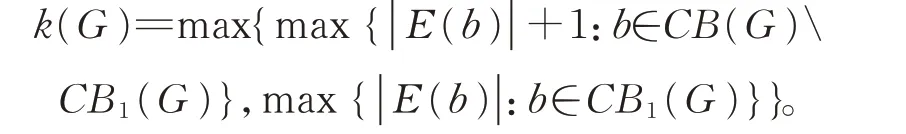
Chartrand 和Wall 在文献[4]中确定了树的哈密尔顿指数。
定理4[4]设T是一棵树。 那么h(T)=k(T)。
在定理4 的基础上,我们首先讨论树的哈密尔顿路指数。设T是一棵树,P是T中的一条极长的路。 那么由CB(T)和CB1(T)的定义可知,如果b∈CB(T)( 或 者 ,b∈CB1(T))并 且E(b)∩E(P)≠∅,那么b⊆P。所以,我们在研究哈密尔顿路指数时,只需要讨论CB(T)(或者,CB1(T))中满足E(b)∩E(P)=∅的枝b。定义

且E(b)∩E(P)=∅}},并且k*(T)=min{k*(T,P):P是树T的一条极长的路}。如果T本身就是一条路,那么我们规定k*(T)=0。下面我们给出树的哈密尔顿路指数。
定理5 设T是一棵树,那么hp(T)=k*(T)。
证明 首先我们证明hp(T)≤k*(T)。根据定理3,只需证明EUPk*(T)(T)≠∅。设P是树T的一条极长的路,使得k*(T)=k*(T,P)。令
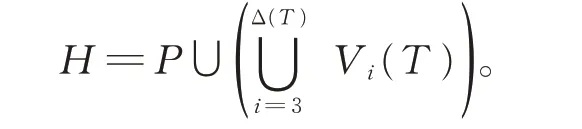
下面证明H∈EUPk*(T)(T)。显然H满足(I)′和(II)。由H的定义可知,H中的分支只能通过树T中属于CB(T)CB1(T)的枝来连结。由k*(T)的定义,我们知道对于H的每一个子图H1,有dT(H1,H-H1)≤k*(T)-1,从 而(III)成 立。 由 于B(T)=CB(T)和B1(T)=CB1(T),以及k*(T)和H的定义可知,对于每一个b∈B(T)且E(b)∩E(H)=∅,有|E(b) |≤k*(T)-1<k*(T)+1;对 于 每 一 个b∈B1(T) 且E(b)∩E(H)=∅, 有 |E(b) |≤k*(T)。 即H满 足(IV)和(V)′。 这 就 证 明 了H∈EUPk*(T)(T)。
下面我们证明hp(T)>k*(T)-1。根据定理3,只需证明EUPk*(T)-1(T)=∅。 用反证法,设EUPk*(T)-1(T)≠∅,并且H∈EUPk*(T)-1(T)。如果H不连通,对于H的分支H1,我们可以找一条最短路P1使 得dT(H1,H-H1)=|E(P1)|(≤k*(T)-2)且c(H∪P1)=c(H)-1。显然,P1∈B(T)。重复这个过程,直到得到的图H~:=H∪P1∪P2∪…是连通的。如果H连通,那么令H~:=H。下面我们断言如果一个枝满足b∈B(T)B1(T)和E(b)∩E(H)=∅,那么b⊆H~:否则的话,b∪H~将会产生一个圈,这与T是一棵树矛盾。注意到B(T)=CB(T)和B1(T)=CB1(T),当 一 个 枝b满 足b∈CB(T)CB1(T)且E(b)∩E(P)=∅时,| |E(b) ≤k*(T)-2;当一个枝b满足b∈CB1(T)且E(b)∩E(P)=∅时,|E(b)| ≤k*(T)-1。由k*(T,P)和k*(T)的定义可知,k*(T)≤k*(T,P)≤k*(T)-1,矛盾。
因此,hp(T)=k*(T)。
Catlin 在文献[15]中给出了确定一个图G是否包含一个生成闭迹的约化方法。运用这个方法和定理1,人们给出了h(G)的一些很好的上界(参见文献[16]-[19])。文献[10]中给出了一个类似的约化方法,用来确定一个图G的哈密尔顿指数h(G)。
设{b1,b2,…,bm}⊆B(G) 且|E(bi)|≥2。 对于i∈{1,2,…,m},定 义 图G的 收 缩 图,记 为G//{b1,b2,…,bm},是指由G通过收缩bi的一条边得到的图,也就是说,将bi(1≤i≤m)替换为一个长度为|E(bi)|-1 的新的枝所得到的图。
熊黎明和刘展鸿在文献[10]中确定了h(G)≥4 的图G的哈密尔顿指数。
定理6[10]设G是一个连通图,b1,b2,…,bm是G中所有长度至少是2 的枝。如果h(G)≥4,那么h(G)=h(G//{b1,b2,…,bm})+1。
在定理6 的基础上,下面我们讨论类似的哈密尔顿路指数问题。在此之前,先给出两个引理,其中第一个引理是线图可迹性的一个特征刻画,与定理1 相类似;第二个引理可由EUPhp(G)(G)的定义很容易得到,所以我们略去它的证明。
引 理7[12,20]图G是 一 个 边 数 大 于 等 于3 的 连通图,则线图L(G)是可迹的当且仅当图G有一条控制迹。
引 理8 设G是 一 个 图,hp(G)≥2,并 且H∈EUPhp(G)(G)。对于H1⊆H,如果P是一条从H1到H-H1的 路,满 足|E(P)|≥2 且P的 内 部 顶点都不在V(H)中,那么P∈B(G)。
我们给出下面的结果。
定理9 设G是一个连通图,b1,b2,…,bm是G中所有长度至少是2 的枝。如果hp(G)≥4,那么hp(G)=hp(G//{b1,b2,…,bm})+1。
证 明 令G′=G//{b1,b2,…,bm}。由 定 理3可知,h p(G′)≤hp(G)显然成立。如果hp(G′)≤1,那么由引理7 可知,G′中存在一条控制迹H′。令b′1,b′2,…,b′m是G′ 中 的 枝,分 别 与G中 的 枝b1,b2,…,bm相对应。令H′′是G的一个子图,它是由H′通 过 将b′1,b′2,…,b′m分 别 替 换 为b1,b2,…,bm得到的图。定义H=(V(H),E(H)),其中
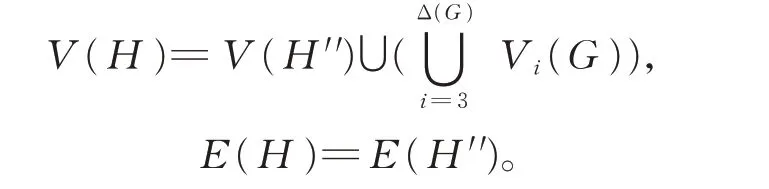
那么H∈EUP3(G):(I)′,(II),(IV)和(V)′显然成立,对于每个H中的孤立顶点u,设b′是一个以u为端点的枝 ,那 么|E(b′)|=1,从 而dG(u,H-u)=|E(b′)|+1=2,(III)也成立。所以,根据定理3可知,hp(G)≤3,这 与 假 设hp(G)≥4 矛 盾。 因 此,hp(G)≥hp(G′)≥2。由定理3 可知,
EUPhp(G)(G)≠∅和EUPhp(G′)(G′)≠∅。
设H∈EUPhp(G)(G),H′是G′中的对应于H的子 图。 由 引 理 8 和G′ 的 定 义 可 知,H′∈EUPhp(G)-1(G′)。 从 而 由 定 理 3 知,hp(G′)≤hp(G)-1。
同理,设H′∈EUPhp(G′)(G′),H是G中的对应于H′的子图。 由引理8 和G′的定义可知,H∈EUPhp(G′)+1(G)。 从 而 由 定 理3 知,hp(G)≤hp(G′)+1。
综上所述,hp(G)=hp(G//{b1,b2,…,bm})+1。
定理9 中的条件hp(G)≥4 是最好可能的:我们下面构造一类图G0,它满足hp(G0)=3,但是hp(G0)≠hp(G0//{b1,b2,…,bm})。 设P=u1u2…u3s…ut是 一 条 长 度 为t的 路,其 中t≥3s+3 ≥15,w,v1,v2,v3是4 个不属于V(P)的顶点。定义G0=(V(G0),E(G0)),其中
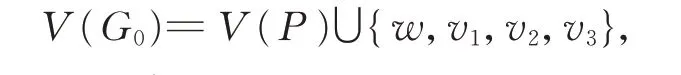
E(G0)=E(P)∪{wv1,wv2,wv3,v1us,v2u2s,v3u3s}。容易验证hp(G0)=3,但是它的收缩图的哈密尔顿路指数为1。
2 哈密尔顿路指数的上界
本节中讨论哈密尔顿路指数的上界。
图G的一个没有割点的极大连通子图称为块。 如果G的一个块只含有一条边,则称它为无圈块,否则称为圈块。 Saražin 在文献[21]中将定理4 推广到了每个圈块都是哈密尔顿的图。
定理10[21]如果连通图G的每个圈块都是哈密尔顿的,那么h(G)=k(G)。
在定理10 的基础上,我们讨论这类图的哈密尔顿路指数。 在图G中,所有的圈块分别记作G1,G2,…,Gs。P是G中的一条极长的路。我们用P将G1,G2,…,Gs分 成 两 类:与P没 有 公 共 边 的 圈块Gi:E(P)∩E(Gi)=∅和与P有公共边的圈块Gj:E(P)∩E(Gj)≠∅。由P的极长性可知,如果b∈CB1(G)且E(b)∩E(P)≠∅,那么b⊆P。
设G是一个图。 如果G有一条哈密尔顿路,规定k*(G)=0;如果G没有哈密尔顿路,但是有一条控制迹,规定k*(G)=1;否则的话,我们按照如下方式定义k*(G)。

并且k*(G)=min {k*(G,P):P是G中的一条极长的路}。如果G≅T是一棵树,它没有圈块,此时令k*3(G,P)=0。从而k*(G)和我们在定理5 之前针对树定义的k*(T)是相等的。 我们在文中仍保留k*(T)的定义,是因为由k(G)的定义引出k*(T)的定义更自然一些。
下面我们研究定理10 中所涉及图类的哈密尔顿路指数。 首先给出下面的引理,它研究了迭代线图中圈块的哈密尔顿性。
引理11[21]如果图G的每个圈块都是哈密尔顿的,那么n次迭代线图Ln(G)的每个圈块也都是哈密尔顿的。
接下来我们给出hp(G)的一个上界。
定理12 如果连通图G的每个圈块都是哈密尔顿的,那么hp(G)≤k*(G)。
证明 如果hp(G)=0,那么G有一条哈密尔顿路。 由k*(G)的定义可知,k*(G)=0。 定理12成立。 如果hp(G)=1,那么由引理7 可知,G有一条控制迹。 此时k*(G)=1,定理12 亦成立。 下面我们假设hp(G)≥2。 根据定理3,只需证明EUPk*(G)(G)≠∅。

因为H包含G中所有度大于等于3 的顶点,所以H中的分支在G中只能通过B(G)B1(G)中的枝 来 连 结。 设H1是H的 一 个 子 图,b∈B(G)B1(G) 是 连 结H1和H-H1的 枝,并 且 满 足dG(H1,H-H1)=|E(b)|。 显 然E(b)∩E(P)=∅。 如果b∈CB(G),那么由k*2(G,P)的定义可知 , |E(b)| ≤k*2(G,P)-1≤k*(G,P)-1=k*(G)-1。 如果b∉CB(G),那么b一定包含在某个与P有公共边的圈块(设为Gj)中:否则的话,b的两个端点位于H的某个圈Ci中,这与b的选取矛盾。 由k*(G)的定义,我们有
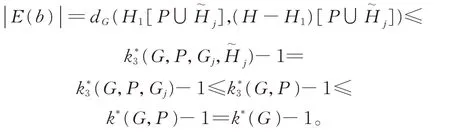
因 此,我 们 总 有dG(H1,H-H1)=|E(b)| ≤k*(G)-1,这就证明了H满足(III)。

因此,我们总有|E(b)| ≤k*(G)+1,这就证明了H满足(IV)。
如 果b∈B1(G) 且E(b)∩E(H)=∅,那 么b∈CB1(G),从而|E(b)| ≤(G,P)≤k*(G,P)=k*(G)。所以H满足(V)′。
这就证明了H∈EUPk*(G)(G)。因此,定理12成立。
定理12 只给出了hp(G)的上界。 针对这类图,我们猜想hp(G)=k*(G)。
猜想13 如果连通图G的每个圈块都是哈密尔顿的,那么hp(G)=k*(G)。
下面我们考虑熊黎明和刘展鸿在文献[10]中给出的哈密尔顿指数的一个上界。 设图G是一个Δ(G)≥3 的 连 通 图。 定 义B0(G)={b∈B(G):G[V(b)] 是G的 一 个 圈},k=max {|E(b)|:b∈B(G)B0(G)}。
定理14[10]设图G是一个连通图,并且不是一条路。那么
h(G)≤max {|E(b)|:b∈B(G)B0(G)}+1。在定理14 的基础上,我们讨论类似的哈密尔顿路指数的上界。 设图G是一个Δ(G)≥3 的连通图,P是G中的一条极长的路,记B0(G)={b1,b2,…,bs}。 我们用P将B0(G)分成两类:

和
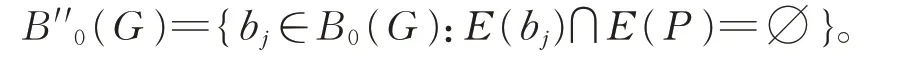
由P的 极 长 性 可 知 ,bi⊆P当 且 仅 当E(bi)∩E(P)≠∅。因此,B0(G)=B′0(G)∪B″0(G)
定义
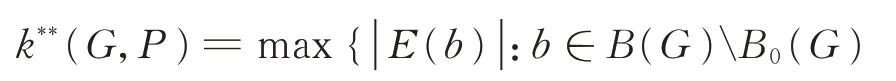
且
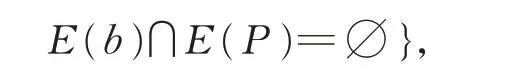
k**(G)=min {k**(G,P):P是G中一条极长的路}。
定理15 设G是一个连通图。 那么hp(G)≤k**(G)+1。
证 明 根 据 定 理 3, 我 们 只 需 证 明EUPk**(G)+1(G)≠∅。 设P是图G的一条极长的路 , 使 得k**(G)=k**(G,P)。 对 于 每 个b∈B0(G),用C(b) 表 示 由V(b) 诱 导 出 来 的圈。 令
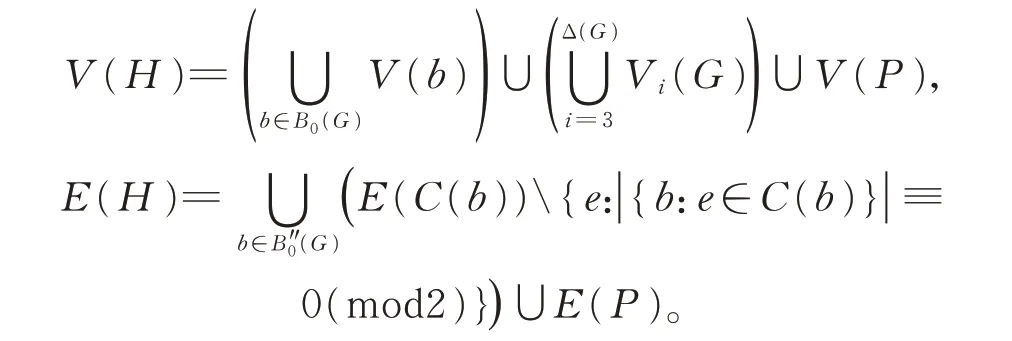
下 面 证 明H∈EUPk**(G)+1(G)。(I)′和(II)显然成立。由k**(G,P)和H的定义可知,任给H的子图H1,dG(H1,H-H1)≤k**(G,P)=k**(G)=(k**(G)+1)-1,(III)成 立。 当b∈B(G),且E(b)∩E(H)=∅ 时 , |E(b)| ≤k**(G)<(k**(G)+1)+1,(IV)成 立。 当b∈B1(G),且E(b)∩E(H)=∅时,| |E(b) ≤k**(G)<k**(G)+1,(V)′成立。这就证明了H∈EUPk**(G)+1(G)。 因此,hp(G)≤k**(G)+1。
定理15 中的上界是最好可能的。 我们构造如下 的 图G0:k≥1,l>k+1 均 为 整 数,P=v1v2…v2l+1是一条长为2l的路,P′=u1u2…uk+1是一条长为k的路,C是一个圈。G0是由P,P′和C通过分别等同顶点vl+1和u1,以及uk+1和C上任意一个顶点得到的图。 此时,k=k**(G0)。 由定理3 可知,Lk+1(G0)是可迹的,但Lk(G0)不可迹。
