复合载荷下不同结构编织人工韧带的有限元分析
2021-08-31王富军劳继红
卢 俊, 王富军, 劳继红, 王 璐, 林 婧
(1. 东华大学 纺织学院, 上海 201620; 2. 东华大学 纺织面料技术教育部重点实验室, 上海 201620)
据报道,全世界每年前交叉韧带损伤人数超过200万[1]。临床上前交叉韧带损伤常使用韧带移植物进行治疗,主要包括自体韧带、同种异体韧带和人工韧带3类[2]。人工韧带具有材料来源广泛,不损伤自体组织以及术后恢复较快等一系列优点,是近年来前交叉韧带移植物的重点研究方向。
目前,大量有关人工韧带的力学性能研究较为单一,大都采用单轴向循环拉伸加载的方式进行表征[3-4]。Guidoin等[5-6]对移植失效的人工韧带进行分析发现,人工韧带的纱线和纱线之间以及纱线和骨之间在膝关节内的相互磨损会造成纤维被磨细,最终导致表层纤维磨损脱落,且大多数移植物的失效是因膝关节的过度拉伸扭转所导致的,因此,人工韧带的复合载荷加载变形研究就显得尤为重要。
随着计算机技术的快速发展,有限元仿真技术逐渐被应用于纺织材料领域,以观察在不同方向外力载荷作用下织物的应力集中分布情况[7-9]。本文通过使用数值计算软件MatLab(R2018a)和三维建模软件Solidworks(2018),建立2种编织结构人工韧带三维模型,并导入至有限元分析软件ABAQUS(2018)创建人体正常步态中,前交叉韧带受到的复合载荷加载环境和计算有限单元解,探究不同结构人工韧带在复合载荷加载条件下的力学响应行为,验证有限元模拟的可行性;同时分析不同结构试样对于复合载荷的应力响应和能量耗散情况,以期为人工韧带的优化设计提供新思路。
1 实验部分
1.1 编织人工韧带的制备
参考目前临床使用较为广泛的商用LARS人工韧带,选取2 222 dtex(192 f)涤纶(上海依石实业有限公司)作为人工韧带试样原材料,其断裂强力为(154.73±0.39) N, 断裂伸长率为(12.01±0.58)%,弹性模量为(5 173.80±25.64) MPa。采用东华大学生物医用纺织品研究中心研制的24锭编织机,分别制备规则编织人工韧带试样(编号AL24-0)和6轴纱三向编织人工韧带试样(编号AL24-6)。使用轴纱的原因是其在编织结构中低屈曲幅度可在初始较小应力作用下承担大部分载荷作用,提高试样的初始刚度,减少人工韧带松弛和不稳定现象的发生率[3]。
1.2 复合载荷加载测试
复合载荷是指正常步态过程中人工韧带在体内时受到的多个方向上的载荷,包括拉伸、扭转和屈曲载荷。基于自主研制的人工韧带疲劳测试装置[10]进行复合载荷加载测试,其主要由拉伸运动模块、扭转运动模块、屈曲运动模块和力学监测模块组成,可实现人工韧带在拉伸、扭转和屈曲方向的加载测试,以及记录水平方向拉伸载荷和测试时间数据,其结构如图1所示。
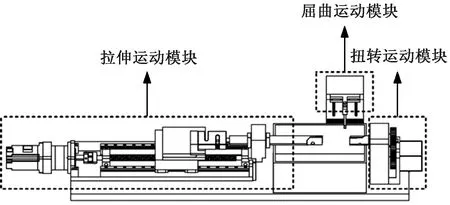
图1 人工韧带疲劳测试装置结构图Fig.1 Structure composition of artificial ligament fatigue testing device
参考人正常步态过程中自体前交叉韧带体内的受力情况,单次复合载荷加载过程[11-13]如图2所示。
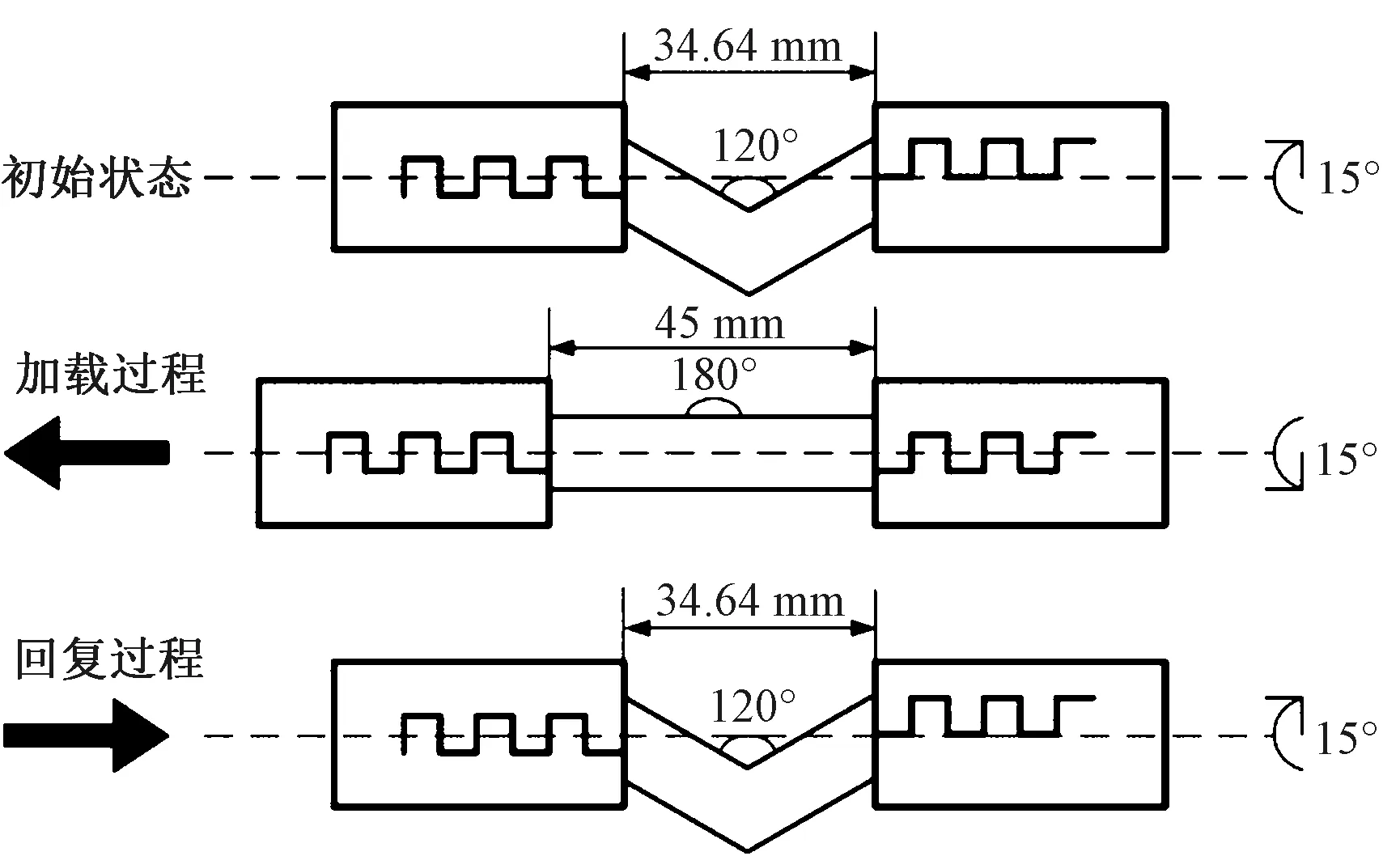
图2 单次复合载荷加载过程Fig.2 Combined loading testing process
1)初始状态时隔距为34.64 mm,试样屈曲呈120°装夹,顺时针扭转15°。
2)加载状态时,试样伸长至45 mm,屈曲呈180°,逆时针扭转15°。
3)结束状态时,隔距、屈曲角度和扭转角度回复至初始状态。加载频率为1 Hz,即1 s内完成1次复合载荷加载回复过程。
2 有限元分析
2.1 编织人工韧带模型的建立
对于管状编织试样来说,纱线的分布可以看作是空间直角坐标系下,其在一定直径圆柱体表面沿正弦方向相互缠绕交织的轨迹。将x轴和y轴作为试样截面方向的相互垂直轴,z轴为轴向,采用式(1)、(2)分别表示逆、顺时针纱线的螺旋缠绕轨迹参数方程[14]。
(1)
(2)
式中:rh为编织螺旋半径,mm;γ为编织螺旋角,(°);α为编织角,(°)。
此外,规则编织结构中顺、逆时针纱线相互交织形成二上二下结构。根据纱线的走向与排布,可推导出逆时针方向第1根纱线的平面屈曲轨迹函数为
(3)
式中:a为纱线直径,mm;β为运动方向相同的2根相邻纱线之间的相位差,(°)。
将纱线的平面屈曲和螺旋缠绕轨迹方程相结合,可推导出逆时针方向第1根纱线的实际空间走向参数方程为
(4)
逆时针方向第2根纱线落后第1根纱线的相位差为β,故可推导出逆时针方向第2根纱线的实际空间走向参数方程为
(5)
后续逆时针纱线与第1根和第2根逆时针纱线具有相同的实际空间走向方程。相应地可推导出顺时针方向第1根纱线的平面屈曲轨迹,以及实际空间走向和第2根纱线实际空间走向参数方程,分别见式(6)、(7)和(8)。后续顺时针纱线与第1根和第 2根顺时针纱线具有相同的实际空间走向参数方程,故经以上分析已完整定义规则编织试样AL24-0 所有纱线的实际空间走向参数方程。6轴纱三向编织试样AL24-6计算方法类似。
(6)
(7)
(8)
本文研究对试样模型进行一定程度的简化,将纱线作为组成试样的最小单元,忽略内部空隙。取rh= 2 mm,α= 50°,a= 0.45 mm,长度为40 mm,并将2种试样的实际空间走向方程输入至MatLab中,计算得到空间坐标点集合,再导入至Solidworks,得到如图3所示的2种编织人工韧带试样的三维模型,最后导入至ABAQUS中以待计算。

图3 2种编织人工韧带试样的三维模型Fig.3 Three-dimensional models of two braided artificial ligament specimens
2.2 有限元分析环境创建
将1.1节获得的力学数据导入至ABAQUS中的Property(属性)模块,赋予纱线非线性以及各向同性材料属性[15]。选用ABAQUS/Explicit显式求解器进行计算,其在计算过程中不需要求解平衡迭代方程,无收敛性问题,在高度复杂的接触问题中可进行较为快速的计算,如模拟纺织结构中纤维及纱线间高度复杂的相互接触作用。求解过程分为2步:第1步将人工韧带试样模型屈曲呈120°,且在扭转端顺时针扭转15°模拟实际测试中的初始状态;第2步将试样伸长至45 mm,屈曲呈180°,且在扭转端逆时针扭转15°模拟实际测试中的加载状态,时间均为0.5 s。在历程输出(history output requests)中设置输出摩擦耗散能(ALLFD)、应力(S)和反作用力(RF)等参数,输出频率为200。设置接触模式为通用接触(General Contact),切向摩擦因数为0.15,法向接触为硬接触[14]。最后进行结构化网格划分,根据前期预实验探究确定单元尺寸为0.1以达到最高仿真效率,单元类型为C3D8I(8节点六面体非协调单元),并提交计算。
2.3 有限元计算结果分析
在后处理模块中提取第2个分析步的水平拉伸载荷-时间曲线,并与实际测试加载过程的水平拉伸载荷-时间曲线进行对比验证,结果如图4所示。2组曲线的上升趋势基本一致:在初始时间段内为试样的屈曲伸直,表现为小变形下的低载荷行为;随后试样被拉伸,载荷线性上升。此外有限元模拟曲线相较于实验曲线具有较高的初始斜率,这可能和有限元模型中纱线自身结构较为刚硬有关。为进一步验证有限元分析的有效性,将2种试样拉伸至极限位置(即1 s)时,载荷的有限元模拟值与实验值进行对比,结果如表1所示。可知,2种试样的理论值和实验值相对误差的绝对值均小于8%,说明不同结构编织人工韧带在复合载荷加载下的有限元计算结果具有一定参考价值。
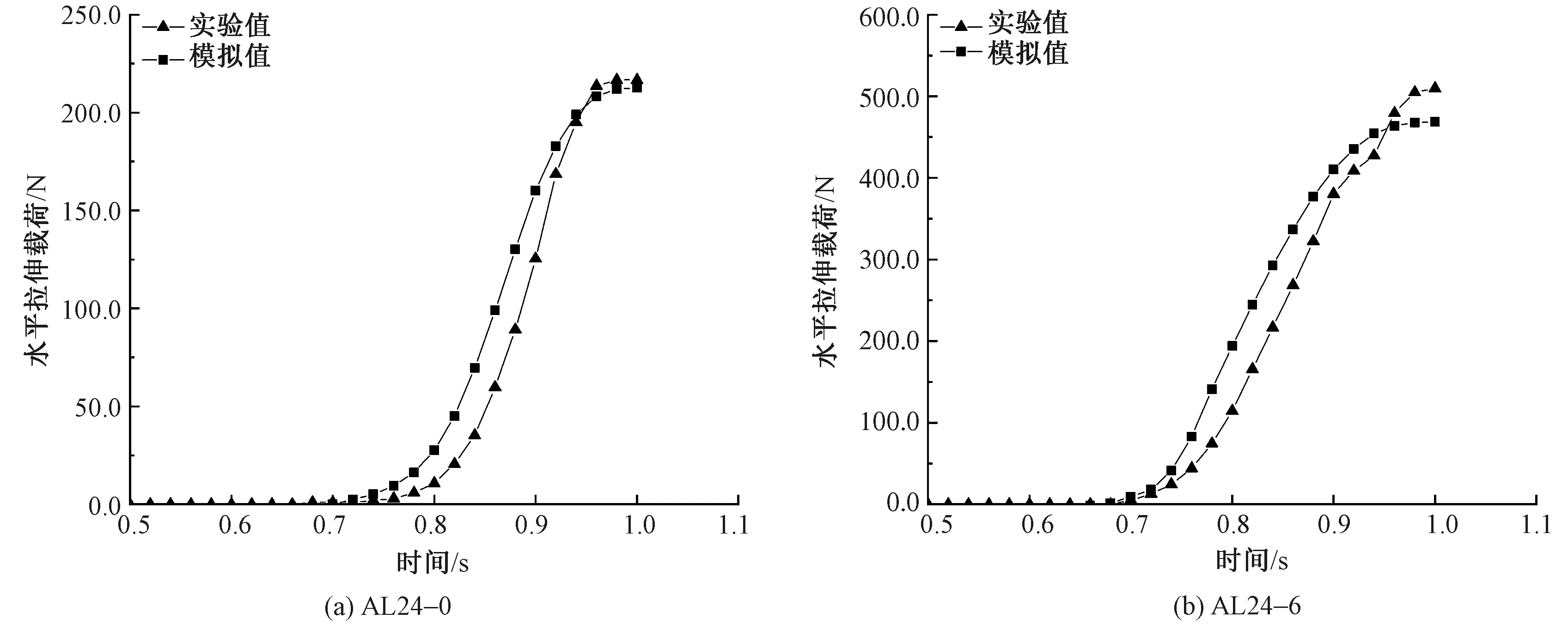
图4 2种试样的有限元模拟曲线与实验曲线对比Fig.4 Comparison of finite element simulation curves and test curves of two kinds of specimens
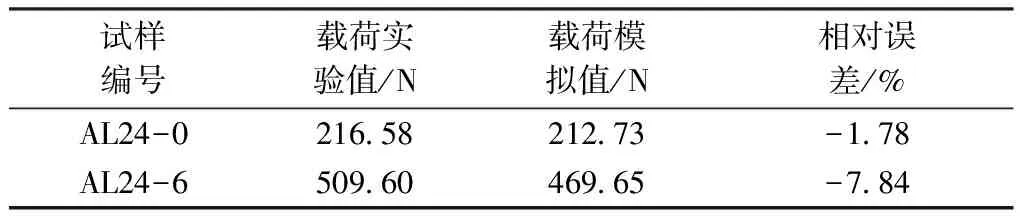
表1 2种试样的有限元模拟值和实验值对比Tab.1 Comparison of finite element simulation and testresults of two kinds of specimens
2种试样复合载荷加载过程的有限元模拟过程如图5所示。模拟流程与实际测试流程具有较高的一致性,即初始状态时试样屈曲呈120°,扭转端面顺时针扭转15°;加载状态时试样伸长至45 mm,屈曲呈180°,扭转端面逆时针扭转15°。
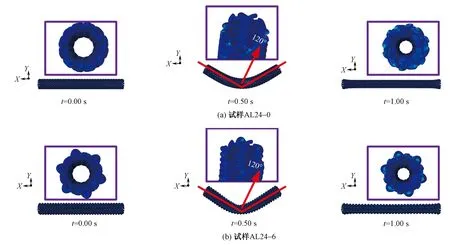
图5 2种试样的有限元模拟过程Fig.5 Finite element simulation process of two kinds of specimens
在后处理模块中显示1根纱线的顺时针、逆时针和轴纱方向的应力分布情况。2种试样复合载荷加载过程中纱线的应力分布情况如图6所示,虚线框中为应力集中区域。试样AL24-0在屈曲状态时,应力主要集中分布于编织纱直线段和交织点处,随后试样被拉伸伸直和伸长,2个方向纱线应力分布较为均匀。试样AL24-6在屈曲状态时,应力主要集中分布于轴纱和编织纱屈曲程度较高部分,在拉伸伸直和伸长后,最终应力主要集中于轴纱处,顺、逆时针纱线承担应力较小。
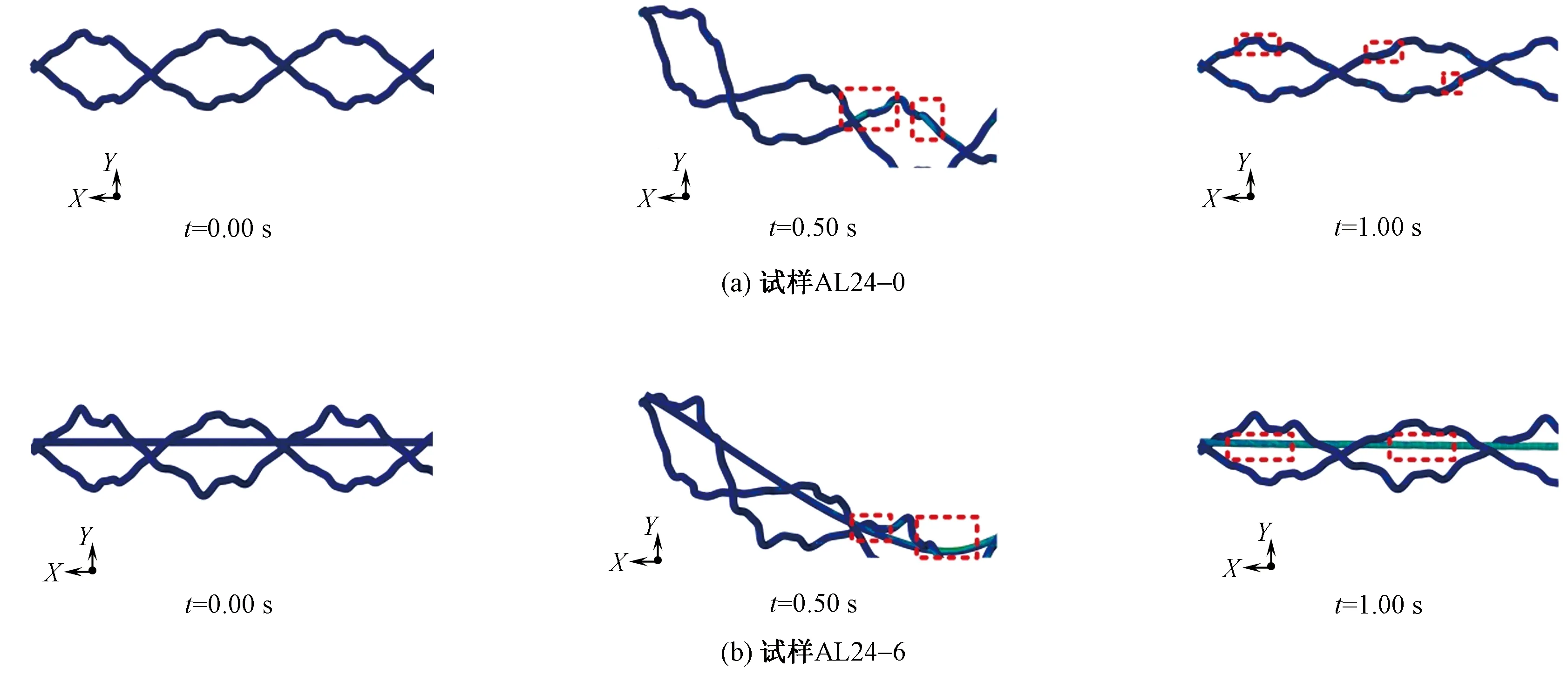
图6 2种试样纱线的应力分布情况Fig.6 Stress distribution of yarns of two kinds of specimens
为提取分析过程中纱线范式等效(von mises)应力随时间变化情况,使用Python(2.7)编写了平均von mises应力值输出脚本。2种试样复合载荷加载过程中纱线的平均von mises应力值如图7所示。可知:试样AL24-0在复合载荷加载过程中,顺时针和逆时针纱线在各时间点平均von mises应力值基本一致,在极限位置时分别为104.18和109.14 MPa, 差值为4.96 MPa;试样AL24-6在复合载荷加载过程中顺时针和逆时针纱线平均von mises应力值计算结果类似,在极限位置时分别为75.29和68.83 MPa,差值为6.46 MPa,且远低于同时刻的AL24-0试样中纱线von mises应力值。轴纱的平均von mises应力值在各时间点远高于编织纱线,在极限位置时为391.05 MPa,进一步验证了轴纱在复合载荷加载过程中起到承载主要应力的作用。

图7 2种试样纱线的平均von mises应力值Fig.7 Average von mises stress values of yarn of two kinds of specimens
2种试样复合载荷加载过程的摩擦耗散能曲线如图8所示。结果表明,试样AL24-6的摩擦耗散能始终高于试样AL24-0,在极限位置时分别为57.55和33.06 mJ,差值为24.49 mJ。由于试样AL24-6具有更多抵抗外力变形作用的交织点,在屈曲至相同角度时轴纱的变形程度更大,因此,需要抵抗更多纱线之间的摩擦作用,摩擦耗散能较高。
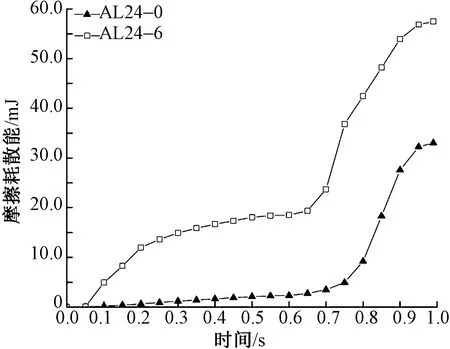
图8 2种试样的摩擦耗散能曲线Fig.8 ALLFD curves of two kinds of specimens
3 结 论
本文使用商用数值计算和三维建模软件成功建立了规则编织和6轴纱三向编织2种结构人工韧带试样模型,导入至有限元分析软件中建立了拉弯扭复合载荷加载环境,并进行有限元计算。结果表明:有限元模拟曲线和实验曲线趋势较为一致;施加复合载荷时,规则编织试样应力在2个方向的纱线上分布较为均匀,而三向编织试样应力主要集中于轴纱,编织纱线承担应力较小,且在加载过程中需要抵抗更多纱线之间的摩擦作用。故在人工韧带医疗器械产品研发中可考虑增添轴纱以提高试样在膝关节腔内的力学稳定性;同时,还需综合考虑轴纱所带来的较高相互摩擦作用。未来可继续探究人工韧带在多次复合加载条件下的力学性能响应,并与有限元分析结果结合以计算疲劳寿命。
