接收机畸变对辐射源个体识别中调制器指纹特征的影响*
2021-08-30史萌恺黄渊凌王桂良
史萌恺,黄渊凌,王桂良
(1.战略支援部队信息工程大学 信息系统工程学院,郑州 450001;2.盲信号处理国家级重点实验室,成都 610041)
0 引 言
辐射源个体识别(Specific Emitter Identification,SEI)技术在无线安全[1]、电磁频谱检测、认知无线电[2]以及自组织网[3]中有着广泛的应用。该技术通过提取射频信号与硬件相关的射频指纹特征(Radio Frequency Fingerprint,RFF),实现对特定辐射源设备的识别,因此能够不依赖于信号内涵实现对发射设备的识别。但是,SEI所使用的特征在信号中的表现普遍比较细微,因此很容易受到接收机自身硬件特性的影响。这一特性为广域运动目标识别、多平台协同识别、识别特征库迁移等应用带来了很大的困难。因此,通过分析接收机畸变对RFF的影响,在接收机设计阶段就考虑抑制其影响是一项具有很高现实应用意义的研究。
现有的SEI技术主要可以分为两类[4]:基于辐射源机理的SEI和基于机器学习的SEI。基于辐射源畸变机理的SEI主要是通过分析辐射源指纹特征的来源和产生机理、构建机理模型或数学表示、估计畸变参数的方式来获得辐射源指纹特征,常用的畸变机理模型有射频振荡器畸变模型[5]、功放非线性畸变模型[6]、正交调制器畸变模型[7]等,常用的数学表示有Hilbert-Huang变换[8]、离散小波变换[9]、调制星座图[10]等。基于机器学习的SEI主要是借鉴语音处理以及图像识别领域的识别方案[11-12],利用近几年机器学习的理论成果来进行特征提取和识别,主要使用的算法有卷积神经网络(Convolutional Neural Network,CNN)和深度残差网络等,但两种技术路线均无法回避接收机畸变对特征产生的影响。接收机本质上是发射机的逆过程,其含有同辐射源畸变类似的不理想畸变,因此获得的RFF中普遍含有辐射源和接收机的耦合特征,在更换接收机后无法保证特征的稳定性[13]。对比两种技术路线,研究这一问题时机理模型在一些方面更具优势:机理模型获得的指纹特征经过了人工设计,具有天然的可解释性,但现有的针对机理的研究中,对接收机畸变进行探讨的相关文献比较少见,尚未形成针对接收机畸变的成熟解决方案。
为了解决以上问题,本文以调制畸变模型为主要研究对象,推导得到了接收机畸变与调制畸变特征的关系,并与实际接收机设计指标相对应,对接收机设计指标提出了建议。通过仿真实验和实际设备实验可以证明,本文讨论结果具有良好的适用性。
1 基于调制畸变的辐射源个体识别方法
本节对一种典型的基于调制畸变的SEI方法进行介绍。文献[14]提出了一种基于机理的畸变估计方法,该方法可以对增益失衡、正交错误、延迟失配、载波泄露进行联合提取,效果较好,并在实际辐射源识别中得到了应用。本文将基于此模型进行分析。
基于机理模型的SEI的基本思路是,建立一个合理的含畸变信号模型,之后利用接收信号和解调结果对模型中的畸变参数进行估计。首先,需要建立用以描述畸变的复基带信号模型:
z(t)=ej(2πf0t+φ)(μ1ρ(t)+μ2ρ*(t)+ξ) 。
(1)
式中:f0为剩余频偏,ξ为载波泄露,φ为信号初相,ρ(t)为复基带调制信号,μ1、μ2为描述了增益失衡以及正交错误的畸变参数。
(2)
式中:cn为传输符号,h(t)为成形滤波器,T为采样周期,τ为采样延迟,τd描述了I、Q两路之间的延迟,该延迟可以通过滑动相关来消除。
(3)
(4)
式(3)、(4)中:GI/Q描述了I、Q两路的增益失衡,ζ描述了正交错误。
根据式(1)所描述的模型,在接收端进行定时估计和匹配滤波后,可以建立在最佳采样点处的接收信号模型:
(5)
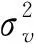
U(f0)Hr=Gθ+v。
(6)

对式(6)应用最大似然估计得到θ的估计结果为
(7)
式(7)中的频偏可以利用快速傅里叶变换(Fast Fourier Transform,FFT) 等传统频率估计方法得到,本文不再赘述。在得到畸变参数矢量θ的估计值后,为了消除初相和信号幅度的影响,同时获得各调制畸变特征的估计值,可以根据式(3)、(4)得到增益失衡和正交错误的估计值:
(8)
(9)
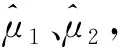
(10)
经过以上步骤,即可根据接收信号和解调符号得到对载波泄露和其他调制畸变的估计结果,但该模型并没有考虑接收机畸变对特征值的影响,针对这一问题需要进一步讨论。
2 接收机畸变对调制畸变估计结果的影响
2.1 滤波器畸变的基本机理
接收机畸变可以分为确定性畸变和随机性畸变,前者主要指接收机放大器和滤波器不理想造成的线性和非线性畸变,后者主要包括各类噪声。随机性畸变可以通过对单一接收机的优化得到改善;在跨接收机识别过程中,需要考虑的主要影响因素为不同接收机之间确定性畸变的差异[15]。
图1给出了超外差结构接收机的基本结构,接收机确定性畸变主要来自于接收通路上在射频和中频模块中包含的多个滤波器的不理想特性、多级功放的非线性畸变、接收机频率源不理想、IQ通道畸变。其中,频率源特性受工作环境影响,能且仅能通过提高频率源设计要求来减小其影响;IQ通道畸变仅存在于零中频结构接收机中,可以通过使用非零中频结构接收机来进行回避。因此,本文优先考虑接收设备滤波器畸变和功放非线性对载波泄露的影响。

图1 超外差接收机基本结构
为了便于分析,可以将各项器件畸变进行简化,将接收机的滤波器特性等效为单个等效滤波器,将功放畸变等效为单个功放,得到简化模型如图2所示。
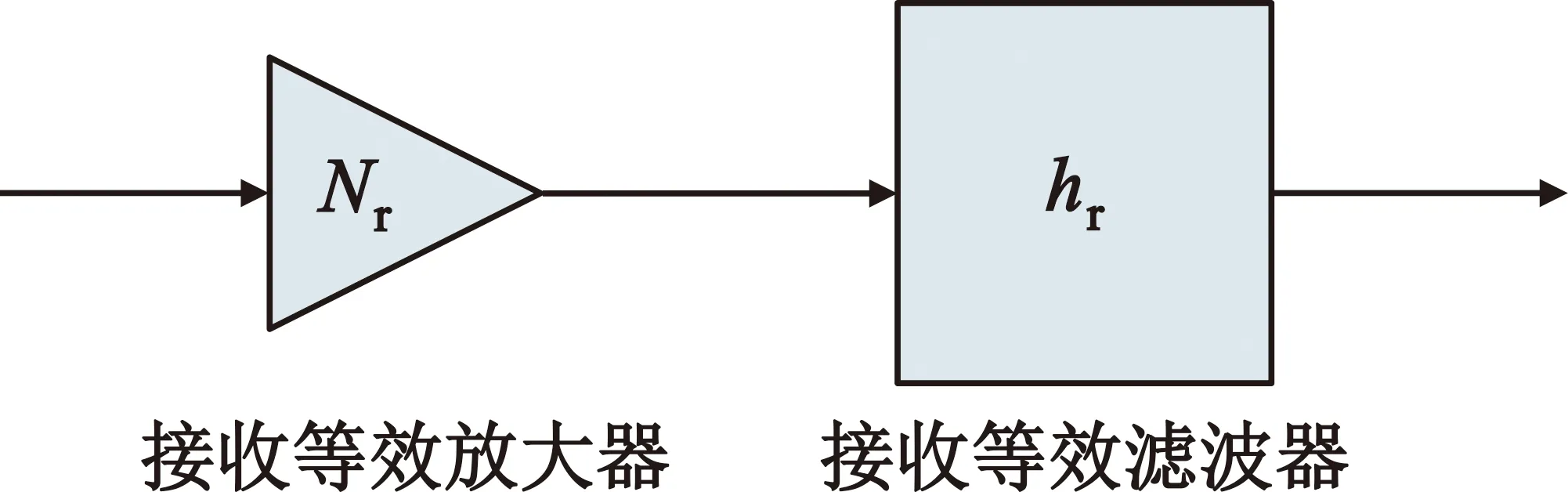
图2 接收机等效模型
该模型中放大器和滤波器的先后顺序会对结果产生影响,本文采用放大器在前、滤波器在后的形式,理由是:大多数接收机射频模块采用的滤波器带宽很大,其带内抖动比较轻微,因此射频部分的畸变主要表现为射频放大器非线性畸变;而在中频模块,滤波器带宽较窄,带内抖动更加明显,且中频放大器线性程度较好,因此中频部分的畸变主要表现为滤波器线性畸变。综上所述,使用图2所示结构能够更加贴近实际接收机畸变情况。
2.2 含接收机畸变的接收信号模型
首先考虑功放非线性。当输入信号为窄带信号时,功放非线性可以使用泰勒级数模型来进行描述,即
(11)
式中:λk为非线性系数,x(t)、y(t)分别为系统的输入和输出。随着阶数升高,系数λk减小,因此高阶次项的影响很小,在接下来的推导中忽略式(11)中阶次高于3的部分。设输入信号x(t)=A(t)·cos(ω0t+φ)并代入式(11),则有
y(t)=λ1x(t)+λ3x(t)3=

(12)
由于接收通路中各滤波器的存在,可以将式(12)中的倍频成分忽略,将余下部分转换到基带。为了便于分析,只考虑采样点处的信号,并且令λ1=1。将式(5)所示的信号进行幅度归一化后代入,可得
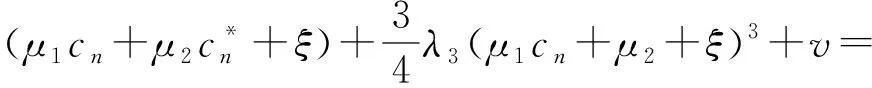

(13)
z(n)=y(n)⊗hr(n)=

(14)
将式(14)改写为矩阵形式:
(15)
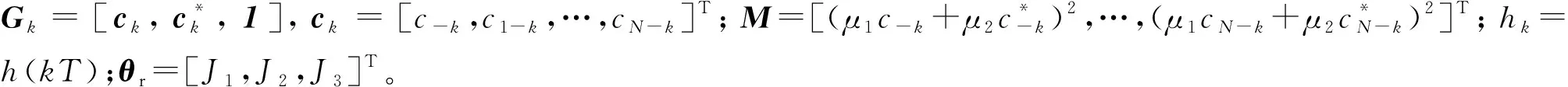
式(15)即为含接收机畸变的接收信号模型。接下来,可以根据式(15)讨论机理模型的估计结果。
2.3 接收机畸变对估计结果的影响
对式(15)所示的信号模型,采用2.1节中介绍的调制畸变估计方法进行特征估计,将式(15)代入式(7),得到估计结果:

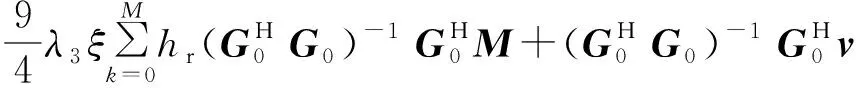
(16)
(17)
将式(17)代入式(16),可得
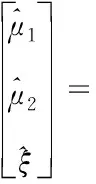
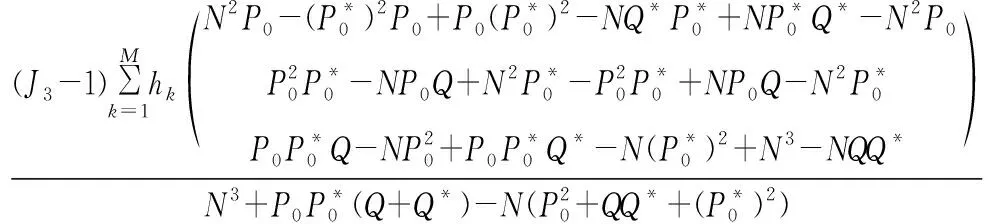
(18)
根据式(18)即可推算传统模型估计结果与特征真值的关系。令N→∞,计算各估计结果的期望,当发送符号位随机序列时,Pk、Q、R、S均为有界量,因此可得最终结果为
(19)
式(19)说明,考虑接收机畸变影响后,调制畸变特征估计结果中的IQ增益失衡和正交错误仍是其真实值的无偏估计,而载波泄露的值则会同时受到线性畸变和非线性畸变的影响。
2.4 接收机设计指标与接收机畸变参数的关系
滤波器设计指标:实际接收机设计的主要滤波器指标为带内抖动。根据式(19),滤波器信号频点处的幅相响应会对载波泄露估计结果产生影响,但在接收机设计指标中的带内抖动指滤波器通带内的波动程度,其值一般大于信号频点处的抖动。为了不失严谨性,不妨设定滤波器在信号频点处的抖动等于其带内抖动。
非线性设计指标:实际接收机设计过程中,一般使用三阶互调抑制IMR3作为接收机非线性指标,其值可以与λk进行对应[21]:
(20)
式中:vs为输入电压。
至此,可以将接收机设计参数与估计结果联系起来,得到
(21)
式(21)描述了载波泄露估计结果的偏移程度与目标载波泄露真实值ξ、三阶互调抑制IMR3、输入信号电平vs、滤波器抖动J的关系。由于滤波器抖动会大于信号频点处抖动,因此得到的理论偏移程度会偏大,即得到的设计指标会在满足需要的前提下更加严格。在实际接收机设计过程中,可以根据接收机工作状态对估计结果的偏移进行估算,进一步确定具体设计指标。
根据2.1节中的讨论,接收机其他设计指标对调制器畸变影响微小,因此在设计阶段不需要进行特殊要求。
根据以上结果,结合实际接收机设计经验,本文认为,通过接收机设计来保证不同接收机之间的特征一致性是可行的,在第3节的设计实例中将进一步证明这一点。
3 仿真与实验
3.1 实验描述
3.1.1 接收机畸变的生成
利用下式生成含有不同畸变的接收机滤波器[16]:
G(f)=H(f)A(f)jφ(f)。
(22)
式中:A(f)和φ(f)分别表示滤波器频率响应的幅度畸变和相位畸变。将其展开为傅里叶级数的形式,并忽略高阶项,可以得到
A(f)=a0+akcos(2παkf),
(23)
φ(f)=2πb0f+bksin(2πβkf) 。
(24)
通过指定αk、βk、ak、bk的值生成具有不同频率响应的接收滤波器。设定滤波器阶数为800阶,按照表1参数仿真产生具有不同频率响应的滤波器,表中同时给出了各滤波器在中心频点(即仿真信号频点)的抖动值。
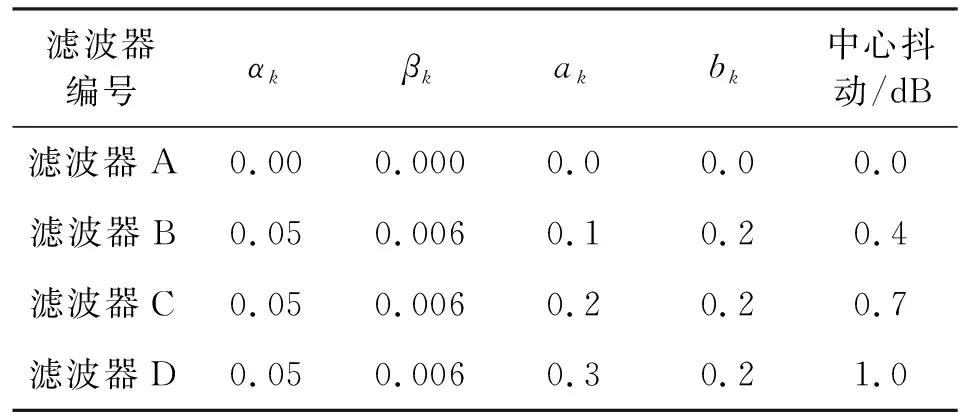
表1 滤波器生成参数设置
非线性特性可以利用式(11),通过设定不同的λk来生成。
3.1.2 信号仿真设置
仿真信号调制方式为正交相移键控(Quadrature Phase Shift Keying,QPSK),发送符号为随机序列,符号速率1 MHz,信号载频2 MHz,采样率8 MHz。在生成发射星座点时叠加载波泄露和调制畸变,载波泄露值ξdc=0.01+0.01i,IQ增益不平衡GI/Q=0.05,正交错误ζ=0.05,信号信噪比设置为30 dB。生成信号先叠加非线性畸变,之后通过畸变滤波器。非线性畸变按式(11)生成,仅考虑三阶非线性,通过改变λ3来改变畸变大小。在接收阶段,对信号进行时间同步和相位同步后,以每20 000个符号作为一次估计的输入样本进行特征提取。
3.1.3 结果评估方法
估计结果主要采用特征偏移量来进行定量描述,特征偏移量具体定义如下:
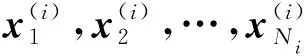
(25)
根据本文的分析,载波泄露的特征偏移量与载波泄露特征值本身成正比,因此为了能够直观描述偏移量的大小,样本在计算偏移量之前应当进行归一化,具体方法是将估计值除以其对应的载波泄露真实值的模,其值的大小表示了偏移值与特征实际值的比值。
3.2 实验结果
根据3.1节中的仿真设置生成信号并进行特征提取,得到不同参数下的估计结果。图3和图4分别给出了调制畸变特征提取结果和载波泄露特征提取结果相对于实际值的偏移量,同时也给出根据计算得到的理论估计值。图中各点均根据特征实际值进行了归一化。

图3 不同滤波器及不同功放非线性参数下载波泄露特征实际偏移量与理论值的对比
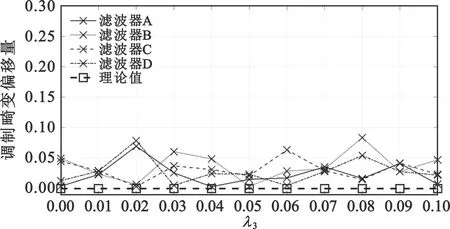
图4 不同滤波器及不同功放非线性参数下调制畸变特征实际偏移量与理论值的对比
图3显示,滤波器畸变及功放非线性均会对载波泄露特征产生影响,其影响与理论推导结果非常相近。图4显示,调制畸变与滤波器和功放非线性的改变并无关系,其偏移量不超过真实值的10%,属于比较轻微的范围,这与理论推导结论相一致。
从仿真信号特征提取结果中可以看出,载波泄露和调制畸变两项特征受接收机畸变的影响与推导结果有很高的一致性。
3.3 接收机设计实例
根据第2节中的分析,本文认为,通过接收机设计来保证不同接收机之间的特征一致性是可行的,因此本文依据该结果对接收机设计进行了实践,并得到了特征提取结果。
在接收机设计阶段,对接收机带内抖动和非线性指标提出要求。接收机为超外差结构,中频频率为70 MHz,相关指标如表 2所示。根据2.1节的讨论,在使用非零中频的接收机时,除以上指标之外的其他指标不需要进行额外要求。
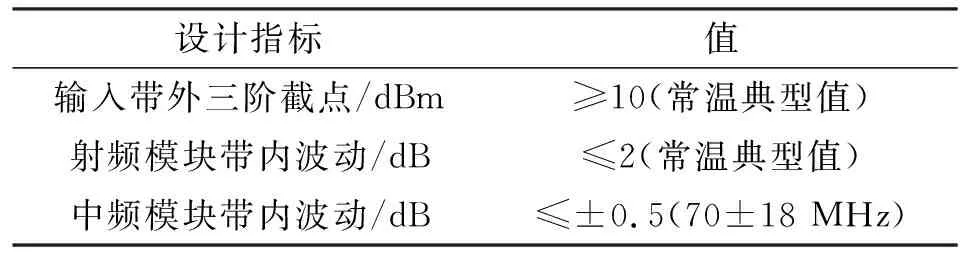
表2 接收机带内抖动及非线性指标
值得一提的是,由于射频模块滤波器带宽较宽,其带内抖动将远大于中心抖动,如果必要,在设计中可以不对射频模块带内抖动进行额外要求。
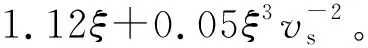
使用2台X310型和5台B210型USRP软件无线电平台作为辐射源,发射载频为1 GHz、符号速率1 MHz的QPSK信号。使用依据表 2参数设计的两台接收机分别对信号进行接收,接收机采样率设置为80 MHz。特征预处理参数与3.1节的设置一致。在获得特征提取结果后,利用支持向量机(Support Vector Machine,SVM)分类器进行分类,统计正确率。分类器输入特征为载波泄露实部和虚部。特征提取结果和识别正确率分别如图5和图6所示。

图5 两台接收机的载波泄露特征提取结果对比
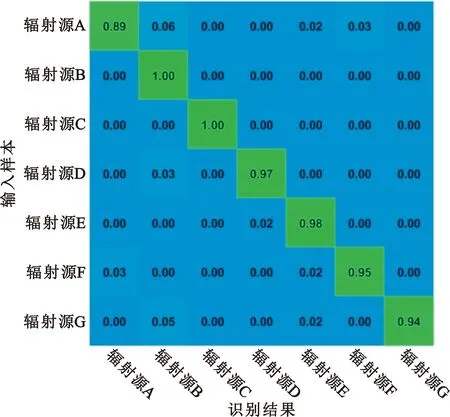
图6 以两台接收机获得的信号分别作为训练集和测试集的识别正确率
图5显示,两台接收机获得的载波泄露特征的稳定性较高,特征偏移并不明显,已经基本可以满足在不同接收机之间通用的要求。图6中的识别正确率则进一步证明了这一点,在使用两台接收机的接收结果分别作为训练集合测试集的条件下,平均识别正确率仍然可以达到96.15%。
综上所述,在跨接收机应用中,通过接收机设计来保证载波泄露和调制畸变特征的稳定性是可行的。
4 结束语
本文分析了在SEI中接收机畸变对调制畸变特征估计的影响,推导得到了非线性畸变以及滤波器畸变与估计结果的数学关系;之后,根据推导结果,将各畸变与实际接收机设计指标相对应,提出了对SEI接收机设计的建议;最后,通过实验验证了推导结果的正确性。
在今后的单接收机识别乃至于跨接收机识别应用中,可以采用本文的方法对接收机畸变的影响进行评估,指导辐射源个体识别接收机设计。本文只考虑了调制畸变(含载波泄露)的提取问题,实际识别应用中往往采用多种特征提取模型进行联合提取,在接下来的研究中可以针对其他特征进行进一步讨论。
